基于GARCH-VaR模型的股票流动性风险度量

刘晓青，杨一文

西北工业大学 管理学院，西安 710072

1 引言

股票市场辗转莫测，参与者随时承受风险。对于流动性风险的度量已经成为风险管理领域的焦点，流动性风险是指经济主体由于金融资产的流动性的不确定性变动而遭受经济损失的可能性。当投资者无法预测随市场环境随时变化的状况时，投资者即面临流动性风险。20世纪90年代VaR方法的应用，即La-VaR（Liquidity adjusted Value at Risk）方法，表明该方法能用来度量流动性风险，且可以将投资者在一定时期、一定概率水平下投资组合可能遭受的最大损失值表示成一个具体的数值。典型如：Hisata和Yamai[1]提出的L-VaR，Shamrouk提出的另外一种流动性风险调整VaR模型（LA-VaR）。国外的研究集中在做市商制度下，我国为竞价市场，与报价驱动市场差别较大，因此不能直接套用国外方法。国内关于流动性风险的研究处于刚起步的理论研究阶段，实证方面比较少。代表性的有：宋逢明等[2-3]总结了怎样将流动性风险纳入已有的研究成果，并结合中国股市的实际，建立了一个对流动性风险进行调整的VaR模型来度量中国股票的价格风险和流动性风险；丁新觉[4]运用研究流动性波动的Amihud的指标测度股票市场流动性，并在流动性与市场收益相关特征研究的基础上，提出了基于GARCH-Copula模型的市场风险与流动性风险的联合度量方法；邓娟、周宏[5]分析了最高成交价与最低成交价之差模型度量流动性风险存在的偏差，同时给出一种新的修正模型来度量流动性风险；王灵芝、杨朝军[6]在对金融危机中流动性风险与市场风险动态相关性研究中，采用时变条件方差方法对流动性风险进行了测度，比较好地刻画了金融时间序列的非对称性、尖峰与厚尾以及波动聚集等特征。

以上实证研究在流动性指标的构建、股票市场的波动拟合以及流动性风险度量等方面进行了详细的探讨。但是，股票市场是由具有不同投资时间尺度的投资者组成的[7-8]，因为投资者对市场具有不同的预期、不同的信息来源和不同的信息解读方式，以及对风险的不同厌恶程度等，因而导致他们具有不同的投资时间尺度，即所谓的市场异质性。市场参与者的异质性行为使得股票市场成为一个多层次的复杂系统，这些不同投资时间尺度的市场行为最终反映在股票价格的波动上，并且，波动在不同的时间尺度上呈现出不同的特征[9]。从中国股票市场的实际情况出发，在充分考虑市场异质性的基础上区别众多投资者的不同预期，完成一个系统、客观的对流动性风险的度量仍具有巨大的挑战性。本文充分考虑到股票价格波动的多尺度特性，通过大量数据模拟和检验，确定了新的流动性度量指标，运用离散小波变换对流动性数据进行多尺度分解，同时，结合GARCH模型从多个时间尺度上分别计算VaR，能更精确地刻画股票市场风险，有助于深刻理解股票市场流动性在不同尺度上的分布结构，为探索股票市场风险开辟了一个更为科学的视角。

2 方法介绍

本文的主要研究思想是计量多尺度上的股票市场流动性风险值。对收集到的股票历史数据，首先运用基于小波变换的多尺度分解方法将数据分解到多个时间尺度上，然后再运用Garch-VaR模型计算各个尺度上的流动性风险值，并通过对VaR值进行检验来衡量模型的有效性。

2.1 小波多尺度分解原理

小波，即持续时间很短的波，一般满足以下条件：

其中，ψ、φ分别称作母小波、父小波（或尺度函数）。多尺度分解就是将一个信号（数值观测序列）表示（分解）成小波函数的线性组合，其中父小波用来表示信号的低频光滑成分，母小波用来表示信号偏离低频趋势的高频细节部分[10]。任意时间序列f(t)∈L2(R)可由正交小波进行多尺度分解或表示：

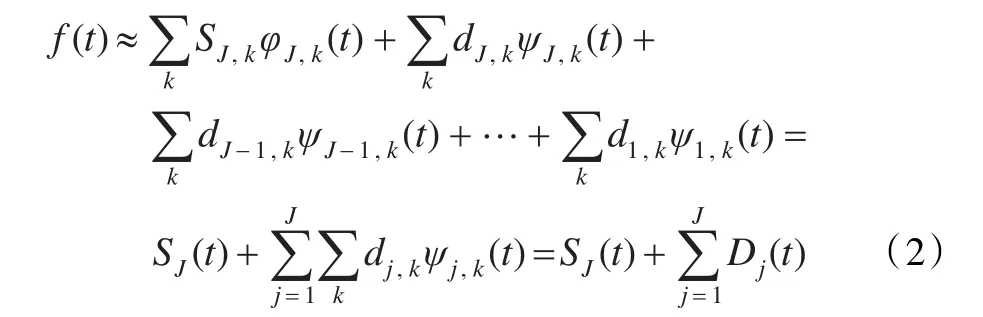
其中，J是尺度分解的层数，k的取值范围是1至对应尺度上小波变换系数的个数，SJ，k，dJ，k，dJ-1，k，…，d1，k是小波变换的系数

函数φj，k(t)、ψj，k(t)由小波函数φ(t)、ψ(t)的伸缩、平移得到：

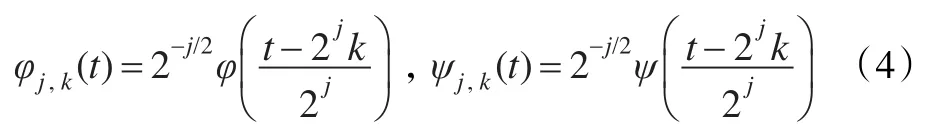
小波系数SJ，k，dJ，k，dJ-1，k，…，d1，k表示小波函数φj，k(t)、ψj，k(t)对整个信号f(t)的贡献程度。系数SJ，k称作平滑系数，表示信号在大（较糙）尺度J上的低频平滑行为，dj，k称作细节系数，表示信号在尺度j上的高频细节行为。式（2）所示的小波分解的示意图如图1。Sj和Dj分别称作原始序列f在不同尺度j上的逼近（或趋势、平滑）和细节，如果原始时间序列f(t)的采样周期为Ts，则对应的采样频率fs=1/Ts，那么经一次分解后，D1的频率范围是2-2fs～2-1fs，对应的时间尺度为2Ts～4Ts；类似地，D2的频率范围是2-3fs～2-2fs，对应的时间尺度为4Ts～8Ts等等，以此类推。这样利用小波变换将信号分解成多尺度（多分辨率）部分、小尺度（精细分辨率）部分和大尺度（粗糙分辨率）部分。值得注意的是，随着尺度的增加，在大尺度上得到的逼近和细节的频率比较低，但是带宽也随之减少，即对低频成分具有比高频成分较高的分辨率。正是由于这一特性，小波变换被誉为数学显微镜。

图1 小波多尺度分解示意图

小波分析是一种窗口大小固定、形状可变的时频局部化信号处理方法，即在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率。因此，小波变换既可以处理平稳信号，还适合非平稳信号、突变信号、孤立奇异性信号。近年来，小波分析被应用于金融波动性建模及相关应用领域，解决传统计量方法无法解决的问题。本文应用的是离散小波变换（DWT），就本文所涉及研究问题的需要，采用了其改进形式——“最大重叠离散小波变换”（Maximal Overlap），因为它具有以下特点：（1）时间序列长度无需是2的整数倍，可以是任意整数；（2）MODWT得到的逼近高尺度和低尺度上的细节具有零相位偏移性，与原始序列在时间上是对齐的，可以方便在不同时间尺度上分析某一市场波动的特点并计算VaR。利用小波进行多层次分解的示意图，如图1所示。

2.2 VaR值理论

VaR值的定义[11]为在给定置信水平下，某一金融资产或证券投资组合在未来特定时间内的最大损失。其数学表达式为：

其中Δp为资产在持有期内的损失值；α为给定的显著水平；VaR为置信水平1-α下的风险价值，即可能损失的上限。

2.3 GARCH-VaR模型介绍

在风险管理中，人们一直在寻求量化的指标来反映和说明整个金融机构或投资组合所承担的各种因素产生的全部市场风险。VaR就是适应风险管理的这种需求而产生的，以规范的统计技术全面衡量市场风险的方法。VaR[12-13]通常对一给定的置信水平，在正常的市场条件下，度量这段时间内最大可能的预期损失。过去VaR值一直被看作是对风险的悲观估计工具，然而，现在它被越来越多的用在了风险的控制和管理中。通过运用VaR工具进行风险估值，机构管理者可以更好的决定资产的分配，并且对投资中的收益和风险进行合理的权衡。对于它的含义，举例来说：例如某银行公布他们的某交易组合，在置信度为99%时VaR值为10元，那么可以理解为，在正常的市场条件下，该交易组合的损失值超过10元的概率仅为1%。更确切的说，VaR值推算出了预计利得喝损失的分布分位数，如果C为置信水平，那么VaR对应的风险值出现概率为1-C。计算VaR的关键是估计某个特定时间段内某资产组合收益和风险的分布，一旦置信水平确定，那么可将该概率下最低损失值确定为VaR。1999年，Altzner等给出了严格的VaR定义，即：

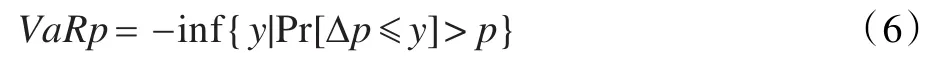
其中，ΔP=P0-PT，P0为投资组合在初始时刻的价格，PT为在T时刻的价格，-inf{Y|A}表示使A成立的全体Y组成的集合的下确界。VaR计量的是资产组合的下方风险（Downside Risk）。VaR的定义既适用于离散的损益分布，也适用于损益序列为连续型随机变量的情形。若为连续型的，则VaR应满足如下等式：

其中，fΔP(y)和FΔP(y)分别表示资产组合随机损益的改了密度函数（PDF）和概率函数（CDF）。

一般计算VaR的方法都是假定式（7）中概率密度函数fΔP(y)服从正太分布。但是大量实证表明金融资产收益不服从正态分布，而具有尖峰厚尾现象。GARCH模型就是改进方法中的一种，它比较好地刻画了金融资产价格时间序列波动的波动性聚集这一特征，即异方差特性，因此结合GARCH模型计算VaR无疑是一个合理的方法。

结合GARCH模型计算VaR符合分布尖峰厚尾的特征，无疑是一个合理的方法[14]。GARCH（p，q）基本的应用形式是：

实际应用中一般假设νt服从标准正态分布、t分布或广义误差分布，例如，假设νt服从标准正态分布，则：

其中，zα为正态分布对应概率为α的临界点或分位数，不等式两端同乘σt：

由收益方程得：

由VaR定义，得到t时刻的(VaR＞0)

其中，Φ(·)为随机变量νt服从的概率分布。

2.4 VaR值的准确性检验

检验VaR模型有效性的方法有多种，本文采用失败率检验方法。假设T为计算出的VaR值序列的样本总数，N为实际损失大于最大损失VaR的样本数量。样本的失败率P=N/T，P0=α，α为计算VaR过程的选择的显著性水平。原假设为H0:P=P0，备择假设为H1:P≠P0。检验统计量为：

统计量LR服从自由度为1的χ2，显著性水平为0.05下临界值为3.84，如果LR＞3.84，拒绝原假设，该VaR模型建立失败。

3 实证分析

3.1 流动性指标选取及数据来源

本文构建流动性指标Lt=rt/tot（rt、tot分别表示t期的日收益率和日换手率，Lt的含义是单位换手率所引起的收益率波动）。从中国沪深两市随机抽取大盘股（长城开发、工商银行、山东黄金、航天动力、招商地产），小盘股（宝通带业、东方园林、GQY、广东鸿图、华星创业）各五支股票2009年—2010年两年的日收益率和日换手率进行指标计算。数据来源为中国经济金融数据库（http：//edu.ccerdata.com/ccerdata/login.aspx），取一只股票（长城发展）的研究过程为例。

3.2 小波分解过程

由单只股票的日收益率/日换手率，得到000021【长城发展】自2009年1月5日至2010年12月10日的流动性指标数据。对该指标序列运用最大重复离散小波变换（MODWT）进行五层分解，最大时间尺度为 32（25）天，所用的小波滤波器为LA8，它是长度为8的与Daubechies最小不对称（Least Asymmetric）尺度滤波器对应的小波滤波器，其最大特点是具有线性最小相位偏移，容易获得零相位小波变换。该指标在不同尺度上的波动细节如图2所示。

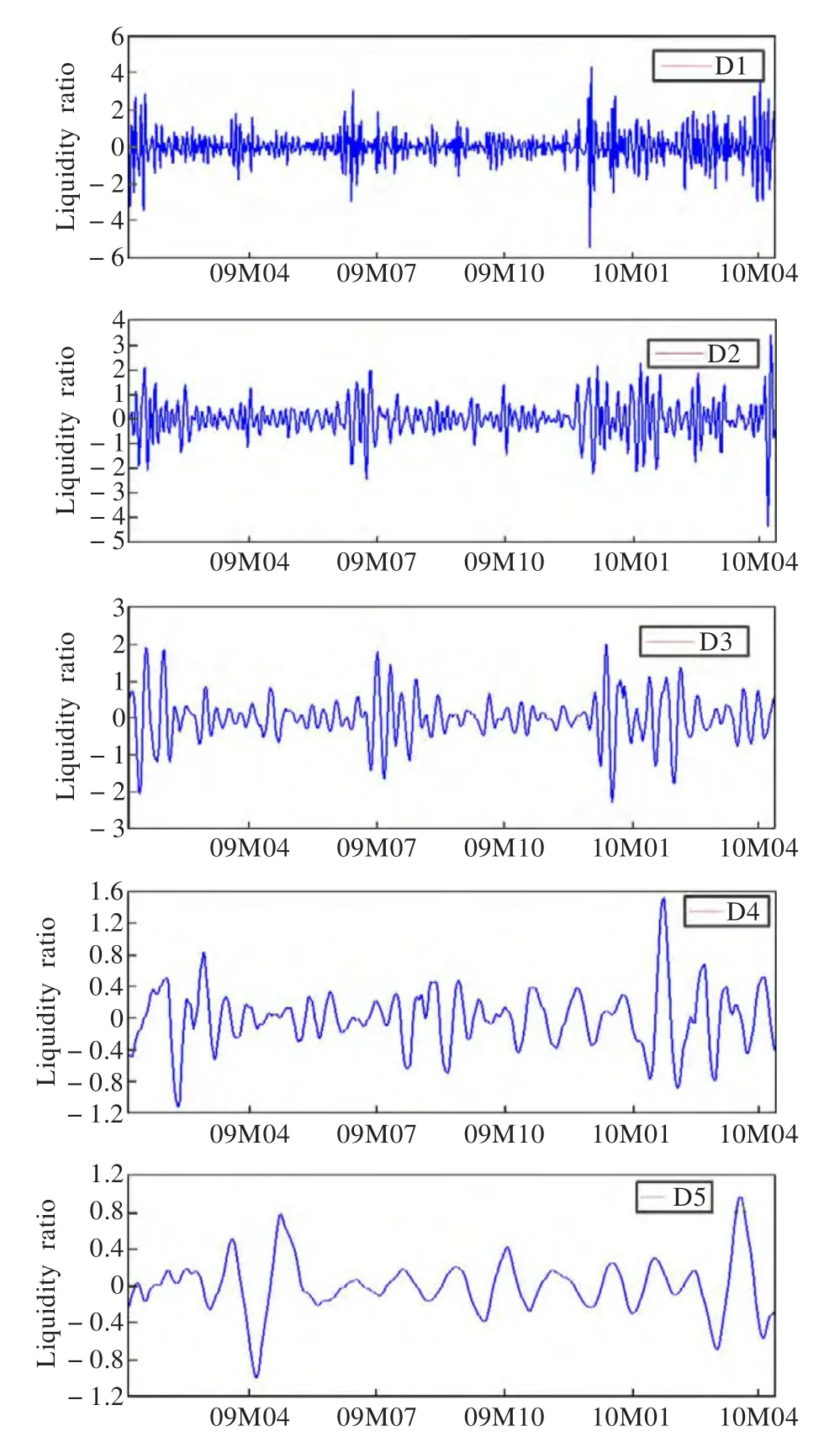
图2 流动性指标在五个尺度上的波动细节

3.3 流动性指标序列多尺度GARCH模型及VaR值计算

根据残差项εt不相关，εt2具有相关性这两个原则，得到GARCH（1，1）结果如表1、表2所示。

表1 条件均值方程参数（000021长城发展）

表2 GARCH（1，1）模型参数

3.4 多个尺度上VaR值的检验

根据上文方法介绍部分所述，针对每一只股票在各个尺度上分别构造统计量LR，10只股票在各个尺度上的LR值均未超过显著性水平为0.05时的临界值（3.841），这表明上述基于GARCH（1，1）的VAR模型对股市流动性这一指标在各个尺度高频分量的波动风险进行了比较准确的度量。选取大小盘各一只作为代表，其结果如表3所示。

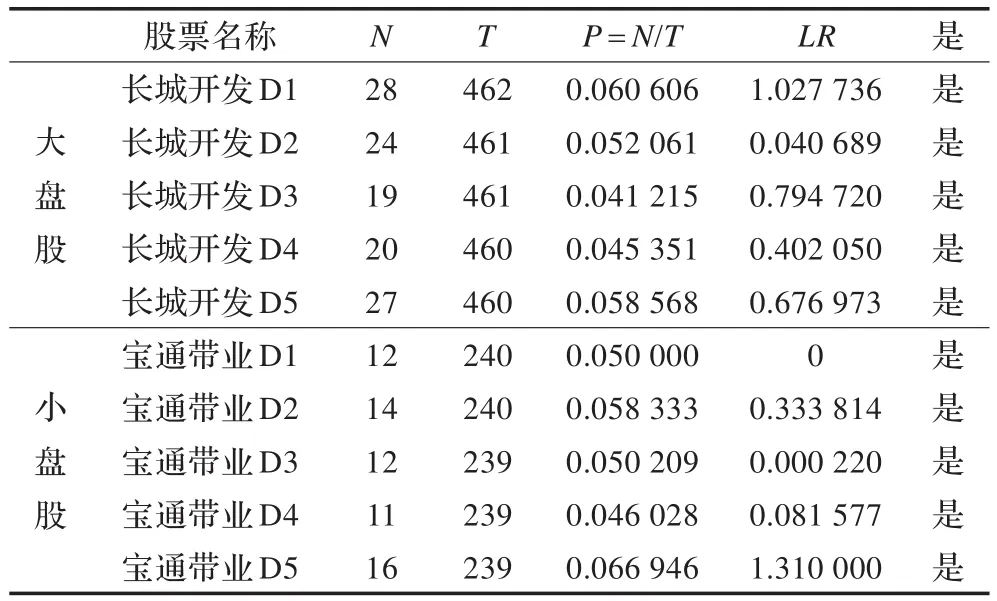
表3 VaR值检验统计表（节选2只为例）

4 结果分析

在证明模型有效性的基础上，本文对大盘和小盘各只股票不同尺度上的VaR值进一步进行统计分析。在本文中，VaR值衡量的是股票流动性风险的状况，因此可以认为，统计结果中VaR的方差一项可以用来衡量总的流动性风险波动状况。以不同的尺度区分作为横轴，以VaR值的方差作为纵轴，对大盘和小盘分别包括的五只股票统计结果构造图表，如图3所示。

图3 大盘股、小盘股多尺度VaR值趋势图

从纵向比较上来看，在图上部的为小盘股流动性风险水平，下部的为大盘股流动性风险水平；纵轴绝对值的大小代表了风险水平的高低。从图中的总体趋势可以看出，小盘股的流动性风险整体上要高于大盘股的流动性风险，这一结论是符合股票市场的规律的。因为资本对风险具有吸收作用[15-16]，在面对同样外部事件的突发影响时，资本额大的大盘股市场可能略有波动，然后很快就能恢复正常秩序，而小盘股市场因其底子薄，规模小，应对突发事件的能力相对要弱，有可能该事件超出其能够承受的范围而最终带来损失。投资者选取的投资市场规模不同，决定了其面对的风险压力的差异。

从横向比较上可以看出，随着小波分解尺度的增加，不论大盘股还是小盘股，其流动性风险水平都出现了显著的下降趋势。结合图2流动性指标在各个尺度上的波动细节图进行分析，随着尺度的增加，分辨率越来越低，突发事件带来的猛烈波动渐趋向柔和，波动曲线变得越来越平滑。这反映出尺度较小时，事件给股票的流动性影响十分剧烈，尺度足够大时，该影响几乎不再发挥作用。由此可以进一步得出这样的结论：股票市场是一个可以随时进出、买卖相对自由的市场，它作为宏观经济的“晴雨表”，同时受内外部多种不确定因素的影响，为了减小不利因素给股票投资者带来的流动性风险，将投资尺度适当放大是有意义的。

[1]Hisata Y，Yamai Y.Research toward the practical application of liquidity risk evaluation methods[J].Discussion Paper，2000，7（4）：83-128.

[2]宋逢明，谭慧.VaR模型中流动性风险的度量[J].数量经济技术经济研究，2004，6（2）：114-123.

[3]郑锴，唐慜.VaR模型中流动性风险的度量[J].经济论坛，2008（17）：114-116.

[4]丁新觉.股票市场风险与流动性风险相关性分析[J].现代商贸工业，2009，6（1）：145-146.

[5] 邓娟，周宏.流动性风险的度量[J].运筹与管理，2010，12（2）：146-149.

[6]王灵芝，杨朝军.金融危机中流动性风险与市场风险动态相关性[J].上海交通大学学报，2010，3（1）：364-368.

[7]Gercay R.Multiscale systematic risk[J].Journal of International Money and Finance，2005，3（2）：55-70.

[8]何建敏，朱林，常松.中国股票市场价格波动的尺度特性[J].中国管理科学，2003，11（2）：1-5.

[9]Samia M.Accuracy and conservatism of VaR models：a wavelet decomposed VaR approach versus standard ARMAGARCH method[J].International Journal of Economics and Finance，2009，9（2）：174-184.

[10]王春峰，姚宁.基于小波变换的多尺度跳跃识别与波动性估计研究[J].管理科学学报，2010，10（3）：63-68.

[11]Bollerslev T.Generalized autoregressive conditional heteroscedasticity[J].Journal of Econometrics，1986，31（3）：307-327.

[12]李克娥，陈圣滔.基于GARCH模型的上证指数的VaR分析[J].财经管理，2008，3（2）：148-149.

[13]陈守东，俞世典.基于GARCH模型的VAR方法对中国股市的分析[J].吉林大学社会科学学报，2002（14）：11-17.

[14]Engle R F.Autoregressive conditional heteroscedasticity with estimates of the variance of UK inflation[J].Econometrica，1982，50（4）：987-1007.

[15]刘洋，刘善存.上海股票市场系统流动性风险溢价研究[J].管理学报，2008，5（2）：113-118.

[16]王春峰，程鹏飞，房振明.中国股市流动性与波动性关系的实证研究[J].北京理工大学学报：社会科学版，2007，9（4）：63-66.