基于图论模型的一类集成电路布线算法

耿显亚，许 峰

安徽理工大学 理学院，安徽 淮南 232001

1 引言

集成电路从20世纪60年代开始，到目前为止已经发展到超大规模集成电路。目前我国集成电路的发展非常迅猛，但是和发达国家的水平相比还是有很大的差距。一般来说一个国家电子工业的增长速率是国家经济增长速率的3倍，而集成电路的增长速率又可以达到电子工业的2倍。这样估算，再过几十年我国的集成电路的市场总额将达到世界集成电路市场份额的四分之一。因此，集成电路的发展任重而道远，只有把集成电路产业发展到世界先进水平，我国的经济才能在世界处于领先地位。

随着集成电路技术的飞速发展，除了工艺技术、设备和材料等方面的不断改进，设计技术的进步也起着举足轻重的作用。在集成电路设计的每个环节和整体设计中都普遍使用CAD技术，随着集成度的提高，芯片内部集成的晶体管数目越来越多，集成电路设计的复杂性也越来越高，要在几十平方毫米的硅片上完成数百万个器件的电子系统的设计，只靠人工设计是完全不可能的，借助计算机辅助设计工具进行电路设计势在必行。由于芯片及其之间的关系可以用图的结构来表示，这样图论的思想方法就可以用到超大规模集成电路设计中。组合优化和图论的方法在超大规模集成电路设计中被广泛地应用，近几十年国内外学者已经做了深入的研究，在此领域中出现了许多优秀的成果[1-8]。德国波恩（Bonn）大学离散数学研究所（Research Institute for Discrete Mathematics）一直从事这一领域的研究，该研究所的主要研究人员大多是图论和组合数学领域的专家，他们自主研发了一套EDA工具（Bonn Tools），被用于上千款IBM芯片的设计。超大规模集成电路设计中许多问题都是NP-难的，在实际应用中常采用启发式算法。本文主要考虑图论的思想方法在超大规模集成电路布线中的应用。

2层曼哈顿模型通道布线是一类很普遍并且研究的比较多的布线类型[9-14]。对于2层曼哈顿模型的通道布线问题，有很多比较有效的启发式算法解决这类问题[15-17]，另外还有很多理论上比较好的改进结果[18-22]。本文主要研究一类2层曼哈顿模型通道布线。

2 通道布线的描述

考虑的是2层曼哈顿模型的通道布线，并且是固定通道的长度。一个通道布线问题是2部的，如果它的线网都包含两个结点，并且这两个结点一个在北面的边界，一个在南面的边界。一个通道布线问题是稠密的如果北面和南面的两个边界上都有属于线网的结点，就是说没有空结点（不属于任何一个线网的结点）。一个线网是平凡的如果该线网只包含两个结点并且两个结点在同一列。另外还有两个与线网有关的图论概念：水平约束图HCG和垂直约束图VCG。

定义1设一个线网Ni，它所占的轨道跨度为Ii，最左边的结点为li，最右边的结点为ri，水平约束图是一个无向图，Gh=(V，Eh)，其中：

V={Vi|Vi表示Ni在图中对应的结点}

Eh={(Vi，Vj)|Ii和Ij不能放在一个轨道上}

在一个通道布线问题中，如果一个线网Ni的结点在北面的边界上，而线网Nj的结点在南面的边界上，那么就说线网Ni与线网Nj有垂直约束关系。

定义2垂直约束图是一个有向图（图1），Gv=(V，Ev)，其中：

Ev={(Vi，Vj)|Ni和Nj有垂直的约束关系}

图1 线网的水平约束图和垂直约束图

水平约束图与通道的轨道高度有密切的关系。如果两个线网有水平约束，那么它们就不能放在同一层轨道上。因此水平约束图的最大团里面的所有线网都不能放在同一层轨道上，故最大团就是通道布线问题轨道高度的一个下界。

如果两个线网有垂直约束，那么它们一定就有水平约束，因此垂直约束图隐含着水平约束图，反之则没有这样的关系。垂直约束图上的每一条有向路上的线网也具有水平约束，故这些结点都不能放在同一水平轨道上，因此垂直约束图的最长有向路也是一个通道布线问题轨道高度的一个下界。

3 通道布线的算法

本章考虑的是2部的且垂直约束图不带有向圈的布线问题，由前面的定义知道2部的通道布线问题表示每一个线网都只有两个结点，并且这两个结点一个在北面的边界上，另一个在南面的边界上。现在假定该通道布线的线网垂直约束图是不含有向圈的。

首先把要考虑的通道布线问题进行公式化的描述。因为垂直约束图不含有向圈，那么就只包含有向路，假定在垂直约束图里面有k条有向路，不妨记为：Pn1,Pn2,…，Pnk，这里ni表示路Pni上包含的线网数目。每一个有向路上的线网记为：Ni1,Ni2,…，Nini(i∈{1,2,…，k})。根据这样的定义，就有下面的式子成立：

为了介绍算法方便，用一个实例进行说明，这样可以清晰地显示算法的进程。在图2的例子中n=13，n*=10，k=3；并且在图中，也画出了该通道布线问题的水平约束图和垂直约束图。

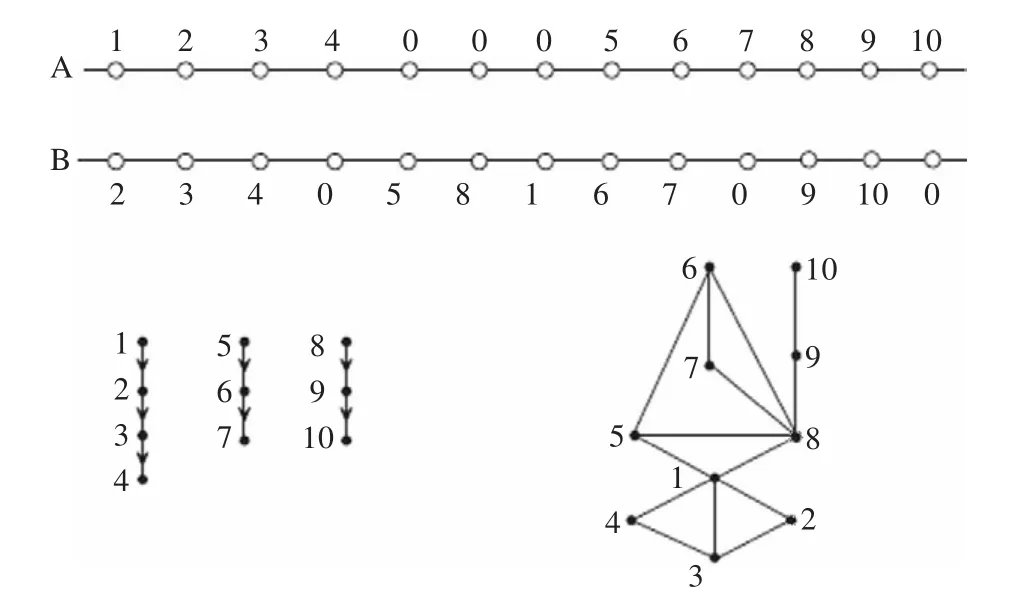
图2 通道布线的一个实例

下面详细介绍针对该问题的算法，该算法分为四阶段。

第一阶段

在进行第一阶段之前，首先把平凡的线网先布好，平凡的线网即是它的两个结点的位置在同一列上，这样的线网布线时就不用分配水平轨道了，就是说可以直接用一个垂直线段连接起该线网的两个结点即可。因此可以不用考虑平凡线网，也可以说通道布线问题不包含平凡线网。在后面的算法中，就不再考虑平凡线网的问题。

这里考虑的布线问题的垂直约束图中只包含有向路，首先，任意的选择一条有向路，不妨记为Pn1。现在就布选择出来的该有向路上的线网。按照从北面到南面的顺序，给每一个线网分配一个水平的轨道，线网的顺序是按照该有向路上的定向来进行，就是说该有向路上的第一个线网分配给它第一个水平轨道，然后依此类推。前面已经定义，本文的通道布线是曼哈顿模型的，就是说一层水平走线，另一层垂直走线，在这里假定上面的一层是垂直走线，而底下的一层是水平走线。根据这个假定，就可以直接布好这个有向路上的线网：对每一个线网，在它所分配到的轨道底层用水平线段处把它的两个结点连接起来，然后在顶层相应的列用垂直线段把水平线段的端点与结点连接起来。因为前面的定义，该有向路上总共有n1个线网，该有向路就占用了n1行轨道。在图3中，P101是有向路（1，2，3，4）。

图3 第一阶段的实例演示

第二阶段

在第一阶段首先处理了一条有向路上的线网，在这个阶段再处理一条有向路上的线网。在剩下的有向路中，随机的选择一条有向路出来，不妨记该有向路为Pn2。现在布这条有向路上的线网，首先考虑线网N21。

在水平约束图HCG中，如果线网N21和N11之间没有边相连，那么就把线网N21放在N11所在的那个轨道上，也就是第一行轨道上。N21的连接方式与上面的线网的连接方式一样，就是底层在轨道上用水平线段，顶层用垂直线段把水平线段的端点与结点连接起来。这样的连接是合理的，因为这两个线网即没有水平约束也没有垂直约束。如果N21和N11在水平约束图HCG中有边相连，那么就考虑线网N21和N12，如果这两个线网在水平约束图HCG中没有边相连，那么就把线网N21放在N12所在的那个轨道上，也就是第二行轨道上，N21的连接方式与上面的线网的连接方式一样。如果这两个线网在水平约束图HCG中有边相连，那么就继续考虑下一行上的线网，即是线网N13与N21在水平约束图HCG上的关系，直到考虑完所有的已经布线的轨道，如果前面已经布线的轨道上面的线网都与N21在水平约束图HCG上有边的连接关系，那么就是说前面的轨道都不能够放置线网N21，只能把线网放在轨道n1+1上，并且这个线网的连接方式与上面的线网是相同的。这样就把线网N21布好了。

然后再考虑线网N22。如果线网N21是放在轨道n1+1上的，那么就直接可以按照顺序把线网N22放在轨道n1+2上。如果线网N21是放在轨道ni(1≤i≤n1)上的，那么首先考虑线网N22和N1i+1，如果它们在水平约束图HCG中没有边相连，那么就把线网N22放在N1i+1所在的那个轨道上，如果它们在水平约束图HCG中有边相连，那么考虑线网N22和N1i+2，依此类推，直到找到N22可以放的那个轨道，然后用上面的方法把该线网用水平线段和垂直线段连接起来。对于N2i(2≤i≤n2)，用上面处理线网N22的方法，可以找到一个合适的轨道把该线网布好。图4是这个阶段的一个实例演示。

图4 第二阶段的实例演示

第三阶段

在前面两个阶段首先处理了两条有向路上的线网，在这个阶段再处理一条有向路上的线网。在剩下的有向路中，随机的选择一条有向路出来，不妨记该有向路为Pn3。现在来布这条有向路上的线网，首先考虑线网N31：策略是找到该线网所能放置的最靠近北面的轨道，因此就从第一行轨道开始考虑。目前在第一行轨道上，有可能有两个线网N11和N21布在该轨道上，至少也有一个线网N11布在该轨道上，N21是否能放置在该轨道是不确定的。所以确定线网N31是否能布在该轨道上，就要在水平约束图上看线网N31与轨道上面的线网之间的关系。如果线网N31和第一行轨道上的线网之间没有边相连，那么就把线网N31放在该轨道上，也就是第一行轨道上。N31的连接方式与上面的线网的连接方式一样，就是底层用水平线段在轨道上，顶层用垂直线段把水平线段的端点与结点连接起来。这样的连接是合理的，因为这个线网与第一行轨道上面的线网即没有水平约束也没有垂直约束。

如果线网N31至少与第一行轨道上的一个线网之间在水平约束图HCG中有边相连，那么就考虑线网N31和第二行轨道上面的线网，这行轨道上的线网也是不确定的，该轨道上至少有一个线网N12，另外还可能有线网N21和N22，具体是否有这些线网要看前面的阶段的情况。现在如果N31与第二行轨道上的所有线网之间在水平约束图HCG中都没有边相连，那么就把线网N31放在该轨道上，也就是第二行轨道上，N31的连接方式与上面的线网的连接方式一样。如果线网N31至少与第二行轨道上的一个线网之间在水平约束图HCG中有边相连，那么就继续朝下面的轨道进行扫描，类似上面的方法，直到找到合适的轨道来布线线网N31。

然后再考虑线网N32。如果线网N31是放在最下面的那个轨道上，就是说这个轨道下面的轨道都没被占用，那么就直接可以按照顺序把线网N31放在下一轨道上。如果线网N31是放在轨道ni上，并且该轨道ni下面还有已经用过的轨道，那么首先考虑线网N22和轨道ni+1上的线网，如果它们在水平约束图HCG中没有边相连，那么我们就把线网N32放在轨道ni+1上，如果它们在水平约束图HCG中有边相连，那么考虑线网N22和轨道ni+1上的线网，依此类推，直到找到N32可以放的那个轨道，然后用上面的方法把该线网用水平线段和垂直线段连接起来。

对于N3i(3≤i≤n3)，用上面处理线网N32的方法，可以找到一个合适的轨道把该线网布好。图5是这个阶段的一个实例演示。

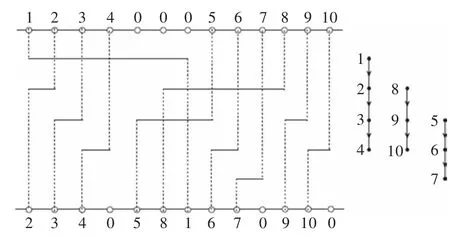
图5 第三阶段的实例演示

第四阶段

前面的三阶段已经处理了三条有向路上的线网，如果这时候有向路还没处理完，那么剩下的有向路Pn4，Pn5，…，Pnk就按照阶段三的方法，就可以把这些线网全部都布线好。这样本文的算法就完成了，下面分析下这个算法的时间复杂性及对比其他的算法所具有的优势。

现在来分析算法的复杂性。

当在第一阶段选择了一条有向路，需要固定的时间来布这条有向路上面的线网；当在第二阶段选择了一条有向路，需要进行n1次比较；当在第三阶段选择了一条有向路，至多需要进行n1+n2次比较。依此类推，当选择了第k条有向路，至多需要进行n1+n2+…+nk次比较。

这样如果这个算法完成，至多需要比较的次数C为：

因为n＞n*=n1+n2+…+nk-1+nk，所以有k＜n。这样由上面的式子就可以得到：

C＜n·n+n2

因为每次的比较需要固定的时间，所以这个算法能在多项式时间内完成。

现在分析本文的算法所得到的轨道上界及与其他算法的比较。

文献[22]给出了该问题的一个算法，该算法对每一个线网分配一行轨道，故总共需要n*行轨道来进行布线。在该算法中，考虑线网之间的水平约束，让尽可能多的线网放在同一行轨道上，布线需要的轨道高度小于或等于n*。下面来进行详细的分析：

情况1如果最长路为Pm，并且把这个最长路首先选择出来，就是说先用前面的nm轨道来进行布线。再选择其他的有向路时，如果都是可以放在前面的nm行轨道中来进行布线，那么算法完成时，就总共需要nm行轨道来进行布线。所以在这种情况下，算法得到的轨道高度为nm，再加上nm＜n*，就可以得到在这种情况下本文算法是更优的。

情况2如果在算法的第二到第四阶段，后面的有向路上的线网都不能用前面已经用过的轨道，就是说每次处理一个线网时，它都会和前面每一行上面的线网在水平约束图上有边相连，只能用一个新的行来进行布线。那么这种情况下，本文算法就同样是每一个线网分配到一个轨道，这样算法完成时候所用到的轨道高度为n*，本文算法就和前面的算法得到的结果是一样的。

情况3如果算法的第二到第四阶段，有些线网可以用前面已经用到的轨道，但是并不是所有的线网都可以用到前面的轨道，这种情况就是介于第一种情况和第二种情况之间，这时本文算法完成时所用到的轨道高度是大于最长路上的点数而小于所有的线网之和。在这种情况下，本文算法同样是优于前面的算法。

由前面的三种情况可知，本文算法能够得到更优的布线轨道高度。

4 结束语

针对一类2层曼哈顿模型的通道布线问题给出有效算法。通道布线问题的线网约束关系可用水平约束图（无向）HCG和垂直约束图（有向）VCG来表示。针对2部且垂直约束图不包含有向圈的布线问题，提出了一个依据图论模型的最优轨道高度布线算法。该算法根据通道上结点的水平约束图和垂直约束图，依次安排好每一个结点的布线轨道，进而通过通孔可以把所有的结点在2层轨道上布线完成。计算分析结果表明，相比较于目前的算法，本文算法可以得到更好的轨道高度。

[1]洪先龙，严晓浪，乔长阁.超大规模集成电路布图理论与算法[M].北京：科学出版社，1998：2-15.

[2]Lee C Y.An algorithm for path connections and its applications[J].IRE Trans on Electronic Computers，1961：346-365.[3]Soukup J.Fast maze router[C]//Proc of 15th Design Automation Conference，1978：100-102.

[4]Hadlock.A shortest path algorithm for grid graphs[J].Networks，1977，7：323-334.

[5]Hightower D W.A solution to the line routing problem on the continuous plane[C]//Proc of the 6th Design Automation Workshop，1969：1-24.

[6]Mikami K，Tabuchi K.A computer program for optimal routing of printed circuit connectors[J].IFIPS Proc，1968，47：1475-1478.

[7]Chiang C，Sarrafzadeh M，Wong C K.A weighted steinertree-based global router[C]//Proceedings of International Conference on CAD，1992.

[8]Heisterman J，Lengauer T.The efficient solution of integer programsfor hierarchical global routing[J].IEEE Trans on CAD，1991，10：748-753.

[9]Caeden R C，Cheng C K.A global router using an efficient approximate multicommodity multiterminal flow algorithm[C]//Proc of IEEE/ACM Design Automation Conference，1991：316-321.

[10]康志伟.一种新的基于关键路径的时延驱动总体布线算法的研究及其实现[D].北京：清华大学，1995.

[11]Huang J，Hong X L，Cheng C K，et al.An timing-driven global routing algorithm[C]//Proc of IEEE/ACM Design Automation Conference，1993：596-599.

[12]Hong X L，Xue T X，Huang J，et al.An efficient timing driven global routing algorithm for gate array and standard cell design[J].IEEE Trans on CAD，1997，16：1323-1331.

[13]Parng T M，Tsay R S.An new approach tosea-of-gates global routing[C]//Proc of International Conference on CAD，1989.

[14]崔颖惟，乔长阁，洪先龙，等.一种基于拥挤度分析的层次迭代PCB总体布线算法[J].微电子和计算机，1995（S）：58-60.

[15]Recski A，Salamon G，Szeszleer D.Improving size bounds for subcases of square-shaped switchbox routing[J].Periodica Polytechnica：Ser EL ENG k，2004，48：55-60.

[16]Yan J T，Chen Z W.Obstacle-aware length-matching bus routing[C]//Proc of the 2011 International Symposium on Physical Design，2011：61-67.

[17]Golda B，Laczay B，Mann Z A，et al.Implementation of VLSI routing algorithms[C]//Proc of IEEE 6th Internat Conf on Intelligent Engineering Systems，Croatia，2002：383-388.

[18]Kohira Y，Suehiro S，Takahashi A.A fast longer path algorithm for routing grid with obstacles using biconnectivity based length upper bound[C]//Proceedings of Asia and South Pacific Design Automation Conference，2009：600-605.

[19]Bui T N，Chauduri S，Leighton F T，et al.Graph bisection algorithms with good average case behaviour[J].Combinatorica，1987，7：171-191.

[20]Garey M R，Johnson D S.Computers and intractability：a guide to the theory of NP-completeness[M].San Francisco，CA：W H Freeman and Co，1979.

[21]Kramer M R，van Leeuwen J.The complexity of wire routing and finding minimum area layouts for arbitrary VLSIcircuits[M]//Advancesin Computing Research，Volume 2：VLSI-Theory.Greenwich，Connecticut：JAI Press，1984：129-146.

[22]SzeszleerD.A new algorithm for2-layer，manhattan channel routing[C]//Proc of the 3rd Hungarian-Japanese Symposium on Discrete Mathematics and Its Applications，2003：179-185.