基于改进理想解法的城市道路建设排序方法

高跃文, 邵春福, 董春娇

(1.天津市渤海城市规划设计研究院， 天津 300451; 2.北京交通大学 城市交通复杂系统理论与技术教育部重点实验室， 北京 100044)



基于改进理想解法的城市道路建设排序方法

高跃文1, 邵春福2, 董春娇2

(1.天津市渤海城市规划设计研究院， 天津 300451; 2.北京交通大学 城市交通复杂系统理论与技术教育部重点实验室， 北京 100044)

为了更加科学、合理安排城市道路建设顺序，提出了基于改进理想解法的城市道路建设排序方法. 首先，借鉴节点重要度- 区位理论的思想，选取路段重要度、道路通行能力、服务水平、道路属性等指标构建城市道路建设排序的评价指标体系，并采用Delphi法和熵值法组合的赋权法对各指标进行量化赋值，以保证研究的科学性和严谨性；然后，结合灰色关联理论，提出了改进的TOPSIS模型，并借鉴灰色关联理论用相对贴近度(综合重要度)这一指标评价各条城市道路建设的迫切性，从而指导道路建设排序. 最后，以北京市142规划但尚未建设的城市主干路为例，通过对道路编号、构建属性数据库、模型带入计算等步骤，得到各条待建道路的综合重要度数值，并通过聚类分析得到能实际指导城市道路建设的施工排序计划. 该案例验证了基于理想解法的决策模型能够科学、合理地解决城市道路建设排序问题. 考虑到城市基础设施的建设排序具有较多的相似性，若对评价指标的选取进行适当修改，可应用于轨道建设决策、社会公共停车场建设决策等领域.

交通规划； 道路交通； 城市道路建设排序； 理想解法； 节点重要度

0 引言

随着我国城市化进程的不断加快，各大城市都在大规模地进行城市基础设施建设，特别是城市道路在建设规模和投入资金规模上都相当巨大，如何合理规划城市道路建设的时序成为各地政府面临的主要问题. 美国在60、70年代采用单目标排序方法研究城市交通建设项目的排序问题，即费用- 效益决策模型，但由于该方法往往导致公共资金分配不公的现象，在80年代以后逐渐被多目标综合评价模型所取代[1-2]. 目前，我国在城市道路建设时序规划方面尚缺少系统的、专门的理论研究和方法. 北京工业大学和交通运输部部公路研究院采用模糊综合评价模型对快速路系统的适应性进行评价[3]，东南大学采用多层次模糊综合评价模型对城市公交网络的规划进行了研究[4]，此外长安大学、天津大学等也进行过公路或城市基础设施建设方面的研究[5-12]. 但是，由于评价对象和目的的不用，每种方法的指标选取各有差异，指标量化分析方法也不尽相同，总的来说，以上各类方法也仅限于实际案例的个体应用.

城市道路系统可以抽象为由大量空间节点构成，本文首先将节点作为一级评价对象，选取节点重要度、道路属性、城市交通系统和政策、投资等作为一级评价指标，形成城市道路建设时序的评价指标体系；然后，借鉴灰色关联理论和理想解法模型计算各条待建道路的综合重要度，得到初步排序结果；最后，通过聚类分析，将计算结果转化为能够指导实际工作的集合形式——道路建设计划.

图1 道路建设时序研究思路

1 城市道路建设排序评价体系构建

1.1 指标选取

城市道路建设排序的评价指标选取需满足以下几点要求：①综合性，各指标之间应存在一定的关联性，能系统地表征城市道路建设的情况；②可比性，评价体系中的各指标需具有一致的计算口径；③可测性，每一个指标均要能够获取数据或者通过计算间接得到；④简洁性，指标的数量应该精简，避免造成混乱. 本论文经过大量指标筛选和评估，提出了城市道路建设排序的三级指标评价体系，如图2所示.

图2 道路建设排序评价指标体系

1.2 节点及路段重要度指标

1.2.1 节点重要度

城市道路在网络空间布局上表现为由节点构成，根据交通区位理论，各节点由于拓扑结构、交通流量和地理位置等方面的差异，在道路网中所起的作用和所处的地位是不同的. 本论文选取节点重要度作为路段重要度的二级评价指标，从经济及人口发展指标、城市道路设施总体指标、交通区位指标3方面对其进行量化计算，从而定量描述道路节点在城市路网中的综合重要程度. 节点重要度可由下式进行计算：

(1)

式中，Ii为区域内节点i的综合重要度；ωj为第j项指标的权重；yij为节点i的第j项指标标准化后的值.

1.2.2 路段重要度

城市道路可看作由若干个路段组成，而路段重要度INij可由路段两端节点的重要度通过加权计算获得：

(2)

式中，Ii为节点i的综合重要度；Ij为节点j的综合重要度；Lij为路段ij的长度；α为修正系数，通常取1.

可见，路段的综合重要度与其两端节点的重要度成正比，道路综合重要度为若干个路段重要度进行加权平均计算后取和获得，即为

(3)

式中，IMij为道路ij的综合重要度；INik为第k条路段的综合重要度；m为路段数；Lk为第k条路段的长度；Lij为道路ij的长度.

1.3 指标量化处理

1.3.1 指标量化

为建立城市道路建设排序模型，本文提出以下基本假设：①各条道路的社会综合效用(社会、经济和环境等方面)是随时间发生变化的；②社会综合效用以时间为变量进行先行叠加. 假设评价的待建城市道路有m条，表示为P={P1,P2,…,Pm}，道路Pi的评价指标用pij表示，即Pi={pij|(j=1,2,…,n)}. 其中，定量指标，如GDP、人口、产业规模、面积等，可从统计年鉴等资料直接获取；定性指标，如城市规划类指标，可以采用Delphi法确定，采用5级制赋值，并用下式进行处理：

(4)

式中，S表示专家数；uijz表示第z个专家为第i条道路第j个指标的赋值.

1.3.2 标准化处理

道路建设排序涉及的指标种类较多，来自社会学、经济学、交通规划等多个领域，故各指标的单位量纲不同，需要对其进行标准化处理，将所有指标值统一到[0，1]范围中，同时不改变原有数据的差异性. 标准化处理的方法比较多，本文采用最大最小值法：

设Xmaxj为m个节点中第j个指标的最大值，Xminj为最小值，即

(5)

定义标准化数据为：

(6)

1.4 组合赋权法确定权重

本文指标体系涉及较多的定性指标(如功能区定位、产业经济政策等)，若简单采用主观赋权法，将导致评价结果有失科学性. 本论文提出将熵值法和层次分析法相结合的方法(组合赋权法)为各评价指标赋权，可以综合考虑主观因素和客观因素在赋权过程中发挥的作用，既能保证指标权重数据值的客观精确，又能依靠主观赋权法准确把握各项指标权重系数之间的排列顺序，从而避免了单独使用某一种赋权法而造成计算结果的偏差或错误. 本文采用线性加权组合法进行权重计算，计算公式为

wj=αw′j+βw″jj=1,2,…,n

(7)

式中，w′j为主观权重向量，由Delphi法确定；w″j为客观权重，采用熵值法确定；α和β表示两种方法的相对重要程度，本文中取α=β=0.5.

熵是分子运动无序度的度量，熵值大，表示系统分子运动的无序度高，在孤立的系统中，分子运动的无序度会由低状态向高状态自发进行，要想使系统由高无序状态向低无序状态转化，必须有外力作用[18]. 因此，熵具有度量不确定程度的特性. 考虑认为决策过程中获取的信息度和信息质量是决策精度和可靠性大小的决定因素之一，故本文采用值法计算客观指标权重. 熵值法计算指标权重可参照以下步骤：

步骤1 计算第j个指标的熵值，即

(8)

步骤2 计算第j个指标的差异系数Gj，即

Gj=1-Ejj=1,2, …,n

(9)

步骤3 确定指标权重，即

(10)

则W={w1,w2,…,wn}表示指标的归一化权重向量.

2 基于改进理想解法的城市道路建设排序模型

2.1 理想解法基本原理

理想解法(TOPSIS)由Hwang和Yoon于1981年提出，是多目标决策分析中常用的一种方法. 其基本原理是根据各方案与正(负)理想方案的远近程度来判断各方案的优劣性，与正理想方案越接近，方案越优；反之，方案越差. 该排序法得出的最优方案应该满足以下条件：距离正理想解最近，距离负理想解最远. (注：正理想解指其各项评价指标均为最优，负理想解指其各项评价指标均为最差. )

但是，在项目决策的过程中往往会遇到下列问题：①某方案距离正理想解最近，但距离负理想解并非最远；②某方案距离负理想解最远，但距离正理想解并非最近. 针对上述情况，需要选取新的函数对理想解法的2个判断指标进行融合，本论文借鉴灰色关联理论来解决该问题.

图4 城市道路建设排序建模概念图

2.2 灰色关联分析基本原理

灰色关联分析是系统之间、各因素之间的定量对比分析，主要描述其因时间而相对变化的特征，根据其变化体特征之间的接近程度来表征其关联趋势，即灰色关联度. 若两个比较的系统、因素随时间变化的趋势类似，则其关联程度较高；相反，关联度较低.

本论文通过计算各备选方案与理想方案之间的灰色关联度来进行最优解方案的排序. 具体步骤如下：

步骤1 原始数据预处理，见本文1.3.

步骤2 确定理想方案和各备选方案pi

当pi=max(pij)时，称为正理想方案；当pi=min(pij)时，称为负理想方案.

步骤3 计算各备选方案与理想方案之间的关联系数.

(11)

步骤4 确定灰色关联度，即计算关联系数的平均值.

(12)

2.3 基于改进理想解法的城市道路建设排序模型

根据2.2中内容，利用灰色关联分析法，将基础数据代入式(11)、(12)计算，分别得到各备选方案与正理想方案和负理想方案的灰色关联系数矩阵，然后根据式(10)中得到的权重进行灰色相对贴近度的加权计算，并根据计算结果进行优劣排序，从而得到各条城市道路建设迫切程度的排序结果.

设

则称

(13)

为正理想条件下的城市道路建设项目.

设

则称

(14)

为负理想条件下的城市道路建设项目.

(15)

(16)

(17)

其中Ii表示待建道路i分别与正理想方案以及负理想方案之间的相对贴近程度.

根据Ii值的大小可对所有待建道路的重要程度进行排序，从而确定各个道路建设项目的建设顺序.

3 实例——北京市主干路建设排序

3.1 路网计算机描述及节点选取

对北京市城区142条规划但未建设道路进行编号、分拆、建属性库，然后根据道路交叉、区位等因素选取重要道路节点(228个，以城市干路网交叉口节点为主)，如图5所示.

3.2 指标选取与模型计算

道路节点评价指标分别选取了经济人口发展指标、道路设施水平指标、交通区位指标等；路段评价指标则选取道路属性、配套设施及拥堵情况等指标. 然后根据本文提出模型计算道路建设的相对重要程度，如图6所示.

表1 北京市主干路建设重要度

图5 节点选取、编号及分布图

图6 北京市主干路重要建设项目聚类结果

3.3 建设计划编制

从表中1能清晰看出各条待建设道路的建设迫切程度，但由于数据量巨大、实际道路建设往往分批次进行等原因，该结果并不能直接用于指导城市道路的建设. 为此，本论文采用Matlab软件对计算结果通过聚类分析进行了简化处理，将排序结果划分为重要建设项目集合、次重要建设项目集合和一般重要建设项目集合3类，政府相关部门可根据该结果进行道路建设计划的分批次编制.

根据Matlab聚类分析结果，北京市待建主干路项目大致可分为3类，如表2、图7所示.

表2 北京市主干路建设计划

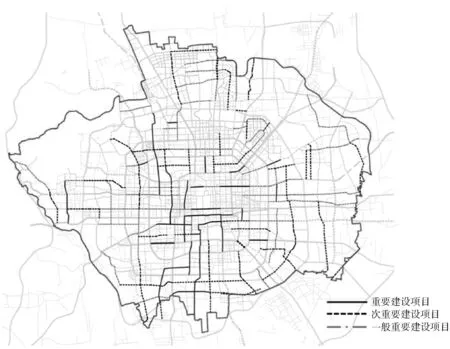
图7 北京市主干路建设计划

4 结束语

本论文建立了内容全面的城市道路建设时序评价指标体系，并借鉴灰色关联理论提出基于改进理想解法的城市道路建设排序办法，为国内城市道路建设时序决策提供了一定的理论依据. 论文在计算路段重要度时，同时引入定性和定量指标，使评价结果更具合理性；采用熵值法对客观指标进行赋权计算，具有一定的创新性. 由于城市基础设施的建设排序具有较多的相似性，若对评价指标进行适当修改，本论文提出的方法将可应用于更广泛领域的研究. 此外，本文在构建评价指标体系时选取了较多定性或属性指标，容易导致评价结果过于主观化，希望其他学者在进行相关方面的研究时能注意该问题并予以解决.

[1] Michael D Mayer， Erill Miller. Urban transportation planning a decision oriented approach[M]. Mcgraw Hill Book Company， 1984： 459-466.

[2] Hwangand C L, Yoon K. Multiple attribute derision making[M]. SpringerVerlag. Berlin, 1981.

[3] 韩亚楠， 周伟， 章锡俏. 快速路系统适应性模糊综合评价[J]. 公路交通科技， 2013， 30(11) ： 139-143.

[4] 周媛， 邓卫， 胡启洲. 基于信息熵的城市公交网络模糊评价[J]. 交通运输工程与信息学报， 2008， 6(2) ： 79-84.

[5] 顾政华， 李旭宏. 主成分分析法在公路网综合评价中的应用[J]. 公路交通科技. 2003， 20(5) ： 71-74.

[6] 李锦华， 张忠秀. 多目标模糊综合评价在城市道路建设项目后评价中的应用[J]. 天津城市建设学院学报， 1998， 4(1)： 13-20.

[7] 李湛. 城市交通运输系统的评价指标体系[J]. 城市规划汇刊, 1995(5)： 51-64.

[8] 苏志欣. 加权灰色关联理想解法在多属性决策中的应该用研究[D]. 成都： 成都理工大学， 2007.

[9] 胡刚， 陈峻， 王炜， 等. 基于层次分析法(AHP)和多指标决策的物流园区建设序列研究[J]. 公路交通科技， 2003， 20(2)： 157-161.

[10] 罗剑， 李旭宏， 李新发. 灰关联分析与变权排序法在公路网规划方案比选中的应用[J]. 交通与计算机，

2006， 24(1)： 21-24.

[11] 张永， 李旭宏， 毛海军. 基于熵权和理想解法的物流中心建设序列决策模型[J]. 东南大学学报， 2005， 35(6)： 967-971.

[12] 曲大义， 王炜， 邓卫. 基于系统层次分析法的公路网规划项目建设序列论证[J]. 中国公路学报， 2000， 13(3)： 64-68.

[13] 李靖华， 郭耀煌. 主成分分析用于多指标评价的方法研究——主成分评价[J]. 管理工程学报， 2002， 16(1)： 39-43.

[14] 陈新， 杨雪， 杨珺， 等. 城市用地形态与城市交通布局模式研究[J]. 经济经纬， 2005(3)： 64-66.

[15] 李霞， 邵春福， 贾洪飞. 土地利用与居民出行生成模型及其参数标定[J]. 吉林大学学报： 工学版， 2007， 37(6)： 1300-1303.

[16] 陈尚云， 高世廉. 我国特大城市土地利用形态与出行总量的距离分布研究[J]. 四川联合大学学报： 工程科学版， 1999， 3(3)： 83-88.

[17] 邓聚龙. 灰理论基础[M]. 武汉. 华中理工大学出版社， 2002.

[18] 邱菀华. 管理决策与应用熵学[M]. 北京. 机械工业出版社， 2002.

Research on Sequencing Urban Roads Construction Based Improved TOPSIS

GAO Yue-wen1, SHAO Chun-fu2, DONG Chun-jiao2

(1.Tianjin Bohai Urban Planning & Design Institute, Tianjin 300451, China; 2.MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing jiaotong University, Beijing 100044, China)

Aimed to sequence the urban roads construction scientifically, the improved TOPSIS was researched in the paper. The paper first chose indicators, including road importance, road capacity, service level, to establish the assessment criterion of road construction on the basis of the theory of node importance and location theory. Meanwhile, all indicators above were quantified and valued via combination of Delphi and entropy evaluation method. Then, the paper proposed an improved TOPSIS based on a grey relational analysis, which could calculate the synthetical-importance-index to guide the sequencing urban road construction. Finally, the paper used Beijing as anexample to validate the theories. Most of urban infrastructures are similar, so the method in the paper can also be used to solve other decision questions, for example railway construction, and parking lots.

transportation planning; road transportation; sequencing the urban roads construction; TOPSIS; node importance

10.13986/j.cnki.jote.2015.05.002

2015- 04- 27.

高跃文(1985—)， 男， 工程师， 交通运输规划与管理硕士学位， 研究方向为综合交通规划、停车规划等. E-mail： tjxiaogao@aliyun.com.

U 491

A

1008-2522(2015)05-06-07