基于强化学习理论的地区电网无功电压优化控制方法
2015-04-14刁浩然孙国忠
刁浩然 杨 明 陈 芳 孙国忠
基于强化学习理论的地区电网无功电压优化控制方法
刁浩然1杨 明1陈 芳2孙国忠3
(1. 电网智能化调度与控制教育部重点实验室(山东大学) 济南 250061 2. 济南大学自动化与电气工程学院 济南 250061 3. 唐山供电公司 唐山 063000)
基于强化学习理论,提出一种实用的地区电网无功电压优化控制方法。方法采用Q学习算法,在动作策略与电网状态的交互中不断学习,得到各状态—动作对所对应的Q值函数,形成电网各种运行状态下最佳的无功电压优化控制策略。方法摆脱了传统电网无功优化求解非线性混合整数规划模型所存在的收敛性问题,同时,相对于基于多区图的无功电压控制方式,由于方法所依据的Q值函数包含电网的全局响应信息,因而,可以综合判断执行控制策略后各变电站之间的相互影响,统一协调地控制各无功电压控制设备,给出所辖电网内的全局最佳控制策略,提高无功电压优化控制效果。通过对220kV变电站及其馈线系统的测试计算,证明了方法的有效性。
电力系统 无功电压优化控制 强化学习 Q算法
1 引言
电压是评估电能质量的重要指标,电压水平直接影响到用户的生产安全。通过调节电网中无功功率分布来实现对电压的有效控制是保障电网安全、可靠运行的关键措施之一。深入研究无功电压控制技术是促进电网发展必不可少的工作,具有巨大的经济和社会效益。
自上世纪70年代末,无功电压控制成为电力系统运行与控制方向的研究热点。其中,由于内点法具备计算时间对问题规模不敏感的特点,受到了学者们的广泛关注[1-5]。文献[1]尝试将原对偶仿射尺度内点法用于求解基于损耗灵敏度系数和相对灵敏度系数矩阵的无功优化模型,其收敛次数比较稳定,具有多项式时间复杂度。文献[2]为提高电压合格率,将电压安全裕度进行模糊处理,用原对偶内点法求解带有模糊约束的逐次二次规划数学模型,在保证网损变化不大的前提下,使电网电压安全裕度有较大提高。在与其它方法的结合使用中,文献[3]将内点法与分枝定界法相结合,分别用于连续变量和离散变量的寻优,据报道有较好的应用效果。文献[4]进一步将内点法与遗传算法相结合,形成一种新的混合优化策略,交替优化连续变量与离散变量,提高了算法的寻优效率。解析方法在电网无功电压优化控制方法中占有重要地位,其从全网角度给出了无功电压优化控制问题的建模与求解方法。然而,由于解析方法对电网结构、参数以及运行量测数据的精确程度依赖较高,复杂的迭代求解算法在对实际系统无功优化过程中常存在鲁棒性不强问题。
另一方面,在当前地区电网,多数变电站都装有电压无功自动控制装置VQC[6-10],此装置基于就地量测信息,依据预定控制策略,对变电站变压器分接头及电容器进行调节。文献[8]利用EMS采集获得电网拓扑结构和运行数据,基于多区图原理对区域无功电压控制设备进行统一调节。文献[9]采用两级无功电压控制思想,基于改进九区图的“厂站级”控制与辐射状电网的“区域级”控制相互配合,在实际运行中,能够提高母线电压和变压器高压绕组功率因数的合格率。文献[10]较为全面地介绍了VQC控制策略及其发展过程。虽然,基于多区图的无功电压控制方法简单易行、运行可靠,但由于电网运行状态变化多样,此类无功电压控制方法往往无法从全网角度设置分区与调节准则,难以给出地区电网具有全局优化特征的控制策略。
由此,在前人研究的基础上,本文提出一种基于强化学习(Reinforcement learning, RL)理论的无功电压控制方法,利用强化学习的渐进学习寻优能力优化地区电网无功电压控制策略,其能够实时给出当前学习阶段下的最佳控制策略,保证无功电压控制算法的鲁棒性。与此同时,由于所提出的强化学习方法利用含有全局信息的值函数进行策略学习,因而能对多变电站实施协调控制,相比较于基于多区图原理的无功电压控制方法,控制效果有明显提升。
2 强化学习原理及Q算法
机器学习是人工智能技术的重要分支,主要分为3类:监督学习、非监督学习和强化学习。其中,强化学习方法由于具有与环境的交互能力,近年来得到较快发展。
强化学习是学习智能体(Learning Agent)在与环境(Environment)的交互中不断试探各种动作,并反馈回报值,渐进获得最优控制策略的过程,其基本模型如图1所示。

图1 强化学习理论的基本模型Fig.1 Basic model of reinforcement learning
如图1所示,首先,学习智能体根据当前的控制策略就环境状态s做出某一动作a,作用于当前环境,使环境状态发生变化。进而,环境将动作立即回报值r反馈给学习智能体,供学习智能体形成新的控制策略。随后,学习智能体将根据新的控制策略和新的环境状态做出新的动作再次作用于环境。学习智能体选择动作的标准是使其获得的累计期望回报值最大化。
Q算法是强化学习理论中发展比较成熟的一种算法,其以离散时间马尔科夫决策过程(Discrete Time Markov Dispatch Process, DTMDP)为数学基础,由Watkins于1989年提出[13-14]。Q算法考察的对象是状态—动作对所对应的值函数,即Q值函数,用Q(s,a)表示[15],代表状态s下执行动作a系统将获得的累计回报值[17,18],如式(1)所示:

式中,s、s′分别为当前和下一时刻的环境状态;a、a′表示相应状态下所选择的动作;γ表示衰减率,且γ∈[0,1],显然,γ=0时,系统只考虑立即回报而不考虑长期回报,γ=1时,系统将长期回报和立即回报看得同等重要。由式(1)可以看出,Q值由动作的立即回报值与后续环境状态下的最佳Q值两部分组成。
状态动作对所对应的Q值可通过在线学习得到[14,17]。在学习过程中,智能体将较高的权重给予当前Q值较大的动作,并根据权重随机选择动作,进而,根据环境反馈结果,对Q值进行更新。设Qi代表Q值函数的第i次迭代值,则Q值可按式(2)进行更新:式中,0<α<1,称为学习因子。较大的α值会加快学习算法的收敛速度,而较小的α值能保证智能体的搜索空间,从而提高Q算法收敛的稳定性[14-16]。

式(2)右边项由两部分组成,前半部分表示了状态—动作对对应Q值的旧值,后半部分表示了本次得到Q值与旧值的差别,并以学习因子作为权重对旧的Q值进行更新。
在智能体的在线学习过程中,Q值将一直更新,直到收敛到一个稳定的结果Q*(s,a)为止。此后,即可以采用贪婪动作策略[14],对于每一个状态,都执行最优动作a*,即:
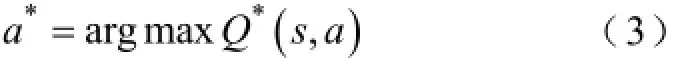
3 基于Q算法的无功电压优化控制
本文基于强化学习Q算法构建220kV变电站出线后辐射状系统的无功电压优化控制策略。下面从无功电压控制问题状态集S和动作集A的选取、Q值函数的构建,以及利用Q算法进行无功电压优化控制的实现流程方面对此问题进行阐述。
3.1环境状态集
对于无功电压优化控制问题,环境状态即电网的运行状态,可由地区电网中待考核的电气量表示,此处选择节点注入功率的功率因数与节点电压幅值为状态量。为计算方便,首先对各量进行归一化处理:
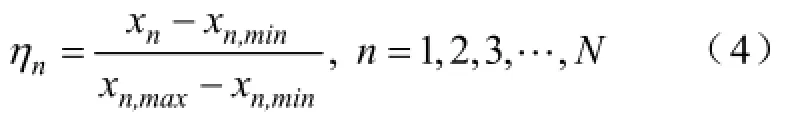
式中,xn为第n个待考核的电气状态指标;N表示考核指标的个数;xn,max和xn,min分别代表考核指标在正常运行状态下的上限值和下限值;ηn为对xn归一化处理后的结果。显然,当ηn>1时,指标越上限;当ηn<0时,指标越下限;0≤ηn≤1表明指标在合格状态范围内;特别地,当ηn=0.5时,认为指标达到最优状态。
进一步,将指标ηn进行状态划分,显然,状态划分越细,对电网运行状况描述得越准确;但过细的状态划分会导致环境状态集合中的元素数目过多,致使学习周期变长,不利于在线控制分析。本文根据现场实际需求,将每个电气考核指标划分为7个状态,如表1所示。

表1 指标状态划分Tab.1 Index states divisions
表1中,指标状态1和7分别代表指标越下限和越上限,在实际运用中,为保证系统安全,可按照距现场安全阈值尚有小范围间距原则设定限定值。yn∈{2,3,4,5,6}为指标合格状态的集合,其中,状态4为最佳状态,其余状态随离状态4的距离变大而依次变差。易见,对于含有N个考核电气量的地区电网,其环境状态集S中共含有7N种状态,每一种环境状态可表示为s={y1,y2,..., yN}。
3.2可行动作集
定义无功电压控制的可行动作集为:当电网处于某状态s时,能够使s过渡到更优状态sʹ的动作策略的集合。根据地区电网无功电压在线控制规程,只有当某一环境状态中含有不合格指标时,电网才会进行无功电压控制设备的调节。显然,每种含不合格考核指标的电网环境状态都有其对应的可行动作集,不同的环境状态所对应的可行动作集一般是存在差异的。
根据现场运行要求,将需进行无功电压优化调节的不合格电气指标分为四类:电压越上限、电压越下限、变压器高压绕组功率因数越上限和变压器高压绕组功率因数越下限。按现场运行规范,同一时刻下,每个220馈线所带网络中不允许有两个及以上的设备同时动作。由此,对于每种需要调节的电网状态,其可行动作集按如下原则确定:
1)电压越上限:可行动作集为在电压指标值ηn大于0.3(指标处于正常状态范围,距电压下限尚有裕度)的本站及上一级变电站切电容器和降变压器分接头;
2)电压越下限:可行动作集为在电压指标值ηn小于0.7(指标处于正常状态范围,距电压上限尚有裕度)的本站及上一级变电站投电容器和升变压器分接头;
3)变压器高压绕组功率因数越上限:可行动作集为在本站及其下级变电站中电压指标值大于0.3的母线上切电容器;
4)变压器高压绕组功率因数越下限:可行动作集为在本站及其下级变电站中电压指标值小于0.7的母线上投电容器。
上述可行动作集的确定原则充分考虑了本站电压和变压器功率因数的实际状态,选择距离限定值尚有较大(30%)可调裕度的电容器和变压器进行调节,其中,投电容器可使待考核电压幅值升高、功率因数升高,而切电容器则起相反作用;升变压器分接头可使待考核电压幅值升高,而降变压器分接头则起到相反作用。强化学习的目的即是通过与环境的不断交互,对于各个变电站,建立状态集内状态与动作集内动作的最佳关联。
3.3 Q值函数
Q值函数用以反映动作执行效果的优劣,其大小与动作执行后的立即回报值的大小直接相关。对于无功电压控制问题,动作执行后,将有两种显著差异的结果,其一是动作执行后,系统仍存在越限的指标,对于此种情况,要尽力避免,为此,将环境状态中越限指标对应的回报值rn设置为-M(M为给定的大值)。另一种情况,当动作执行后,系统状态指标达到最佳值(如电压为标幺值1.0),对于此种情况,将该指标对应的回报值设置为+M。
对于其余情况,采用考核指标与最优值之间的欧氏距离来定义回报值,如式(5)所示:式中,ηn,opt为状态量的最佳值;ηn,max为指标越限边界值。
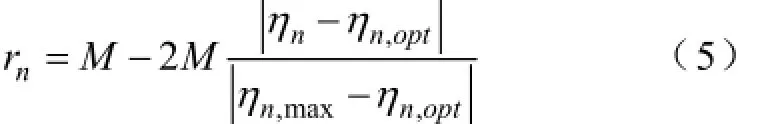
由式(5)可以看出,每个指标对应的回报值在区间[-M, +M]内连续变化。而对于动作a的整体回报值可由各指标回报值加和得到:

从而,Q(s,a)可根据式(1)求得,并在学习过程中,依据式(2)不断更新。
3.4优化流程
为了快速跟踪电网的实时状态变化,使Q(s,a)有较快收敛速度,本文将式(2)中α定为0.99。同时,鉴于后续状态的控制受当前状态控制结果的影响较小,折扣系数γ设定为0.1。基于Q算法设计的无功电压优化控制流程如图2所示。
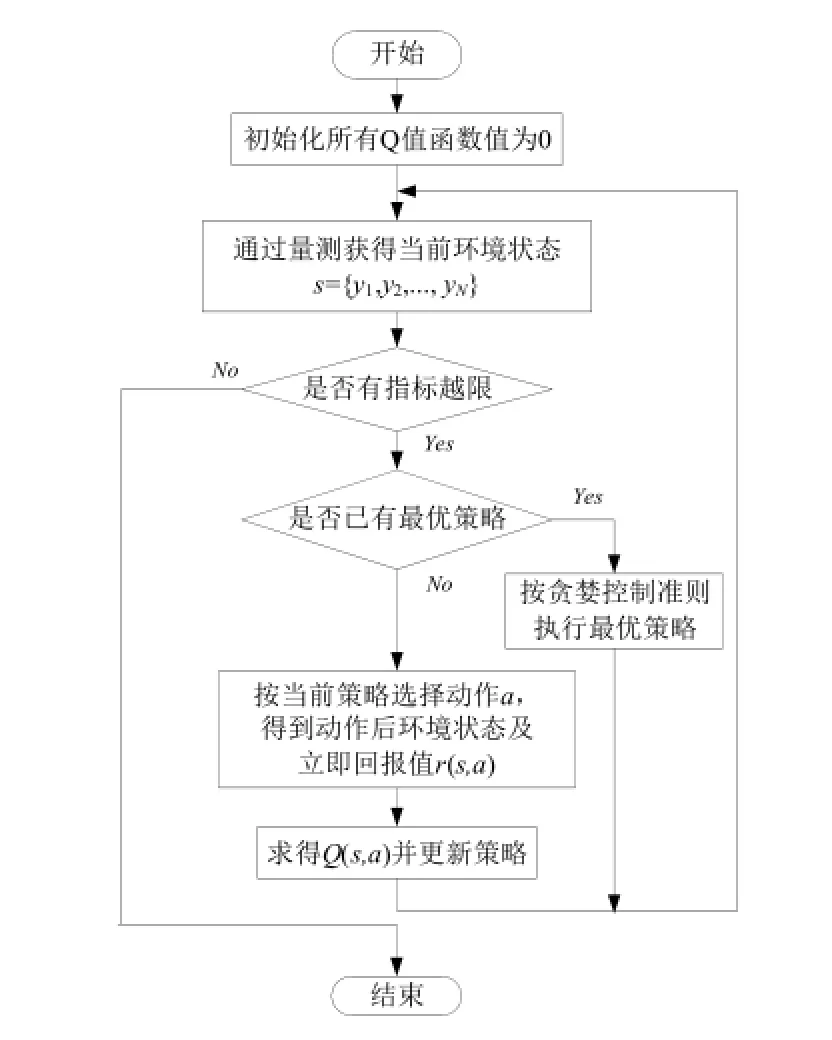
图2 无功电压优化过程流程图Fig.2 Voltage and reactive power optimization process flow chart
如图2所示,电网实际控制时,学习智能体将不断监测电网状态,当出现越限指标,智能体将根据当前适用策略,选择控制动作作用于所辖区域内电网,进而根据动作结果形成的新的电网状态,更新策略并形成新的动作指令,如此反复,直到所辖区域内没有越限指标为止。智能体控制时间间隔按现场对设备控制间隙的要求设定。
智能体所能辨认的状态以及所得到的回报值由所辖电网内所有的指标量构成,依据强化学习理论,智能体选择可行动作作用于当前电网状态,并不断试探其执行时序,最终选择Q值最大的动作策略,实现基于多区图无功电压控制方式难以实现的多站全局控制效果的最佳化。
4 算例分析
本文以图3所示的一个处于山东滨州的220kV变电站及其馈线系统为例,验证本文方法的有效性。该系统共包含三个电压等级的变电站,220kV变电站高压侧母线接有一台发电机。3、6、7、11、12、13节点为负载节点,并有无功补偿电容器。六台变压器均具备有载调压功能。

图3 算例电网馈线系统Fig.3 Example of grid feeder system
不失一般性,图3算例系统选取的考核电气量指标为220kV关口变电站的功率因数和与用户直接相连变电站的低压侧电压幅值,因而,环境状态总数为77=823543个。但实际上,由于电网运行规律性很强,正常运行情况下,绝大部分状态不可能出现,例如,不会出现七个指标都不合格或者多数指标不合格的状态。所以,智能体所要学习与形成策略的状态数量并不多,运行中最优控制策略的形成较为容易。
算例采用潮流计算结果模拟实际电网运行中用量测设备获取的状态量。在学习过程中,为描述方便,本文将所有的动作策略映射为数字指令,其对应关系如表2所示。
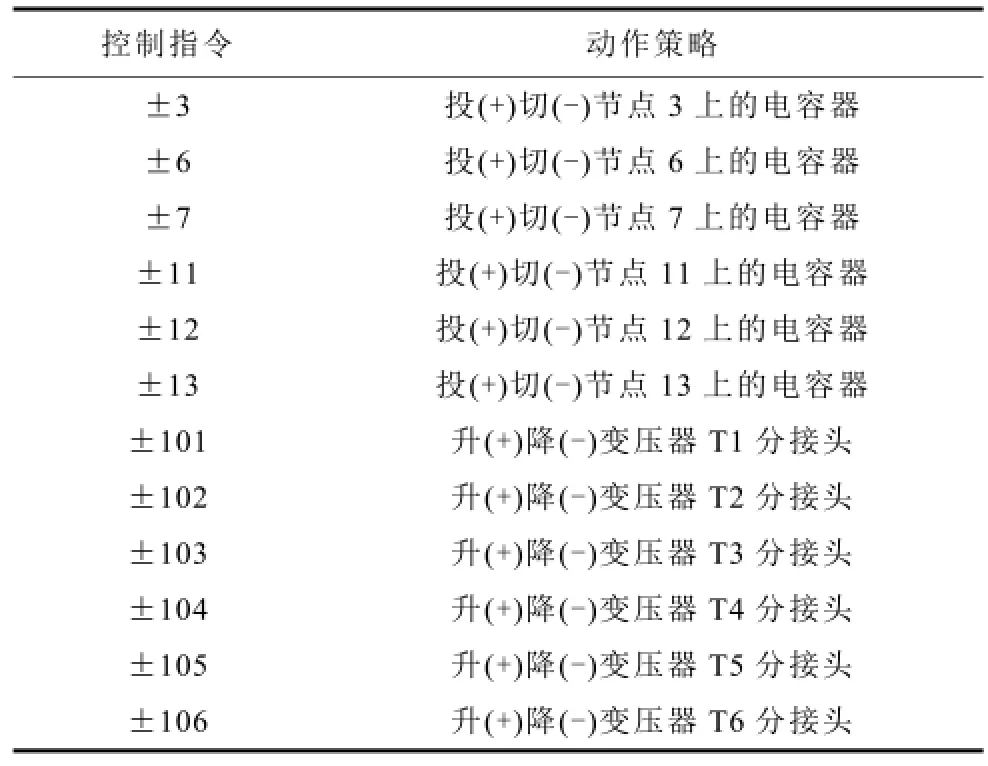
表2 算法控制指令与动作策略对应表Tab.2 Action strategies and corresponding algorithm control commands
根据示例电网实际运行情况,将存在指标越限的部分环境状态列于表3,对本文方法的有效性进行说明。表中,状态量s={y1, y2, y3, y4, y5, y6, y7}由变压器T1的功率因数和节点3、6、7、11、12、13的电压幅值按顺序构成,系统依据环境状态量,按照图2所示流程进行优化控制策略的强化学习,收敛时所得的越限环境状态对应的控制策略及其Q值如表3所示。

表3 控制策略及Q值Tab.3 Control strategies and Q values
对表3所示状态优化控制策略选择的合理性分析如下:
第一种环境状态中,变压器T1的功率因数以及第7、12、13节点的电压越下限。在只允许调节一个设备的情况下,投13节点上的电容器得到的Q值最高,策略最佳。投13节点电容器后的环境状态为{3,3,2,1,2,1,2},投12、7、11节点电容器后的环境状态分别为{4,3,2,1,2,1,1}、{3,3,2,1,2,1,1}、{3,3,2,1,3,1,1}。通过对比,可以看出:13节点电容器投入后,不仅所有指标都恢复合格,而且13节点电压幅值的状态达到‘2’,更趋近于理想状态,说明此时投13节点的电容器对电压提升的效果更明显,所以,该策略对应的Q值高于在7、11、12节点投电容器的Q值。
第二种环境状态中,T1功率因数越下限,但对12节点投电容器的策略得到的Q值最大,投12节点电容器后的环境状态为{3,3,2,2,2,2,2},投13、7、3节点电容器后的环境状态分别为{3,3,2,2,2,2,2}、{3,3,2,2,2,2,2}、{4,3,2,1,2,1,1}。从动作后的状态可以看出:此时投12、13、7节点上电容器对指标的改善效果是非常相近的,但通过式(1)(2)计算得到投12节点电容器的回报值更大一些。投3节点上电容器对T1功率因数提高比较明显,但是对下级35kV和10kV的变电站母线电压的提升效果很小;而投12、13、7节点电容器补偿无功功率的同时,也能够显著提高35kV、10kV变电站母线电压,降低了有功功率损耗,相比之下,投3节点的电容器策略回报值明显更低。控制结果说明本文方法可以充分利用其他变电站的调节动作,从系统全局考虑,给出最佳的控制策略,克服了基于多区图原理的无功电压控制方法只考虑本站可调设备的缺陷。
第三种环境状态中,节点7、12电压越下限。升T1变压器分接头环境状态为{4,3,3,1,3,1,1},其Q值最大,策略最佳。投12、7、6、3节点上的电容器后状态分别为{5,3,3,1,3,1,2}、{5,3,3,1,3,1,1}、{5,3,3,1,3,1,1}、{5,3,3,1,3,1,1},可以看出投电容器操作使T1功率因数明显偏离最优状态,趋近于上限值,故其回报值低于最佳策略回报值;同样可以看到,升T3分接头后的状态为{4,3,2,1,2,1,1},其升压效果不如T1明显,升T3分接头后指标y3、y5的状态为‘2’,而升T1分接头后其状态为‘3’,更趋近于最优状态。所以升T1变压器分接头是本方法的最佳策略,体现了本文方法对全局统筹考虑的能力。
第四种环境状态中,节点13电压越下限。而投节点12上的电容器后状态为{5,3,3,1,3,2,1},获得最大回报值,投13节点电容器后的状态{5,3,3,1,3,1,2}与投12节点电容器后状态区别很小,但Q值作为一个连续的数值,经式(1)(2)计算,前者得到Q值略低于后者。投6、7节点上的电容器后状态为{5,3,3,1,3,1,1},其y6指标的状态‘1’低于投12节点电容器后的状态‘2’。升T3、T6分接头后的状态均为{4,3,3,1,2,1,1},其指标y5、y6的状态均低于投12节点电容器后的状态。综上所述,投12节点上电容器Q值最大,体现了本文方法能够考虑变电站之间的拓扑连接关系,利用全局最有效的电压支撑点改善电压质量。
由上述分析可见,本文所提出的基于Q学习的地区电网无功电压优化控制方法,通过学习智能体的在线渐进学习,可自动学习获得电网各运行状态下最佳的无功电压调控策略,决策过程不仅具有鲁棒性,而且方法具有全局寻优的能力。
5 结论
本文基于强化学习理论,提出了一种新的无功电压优化控制方法。该方法利用Q算法的在线学习功能和良好的收敛性能,能够在线给出当前学习阶段下无功电压控制设备的最优控制策略,保证了无功电压控制的鲁棒性。同时,方法弥补了多区图控制原理在局部控制过程中变电站之间设备难以协调的缺陷,能够实现所辖电网区域内无功电压控制设备的协同优化。文章通过对滨州电网实际系统的仿真计算,验证了所提出方法决策的有效性与结果的合理性。
[1] 刘明波, 陈学军. 基于原对偶仿射尺度内点法的电力系统无功优化算法[J]. 电网技术, 1998, 22(3):24-28.
Liu Mingbo, Chen Xuejun. Prime-dual affine scaling interior point method based reactive power optimization in power system[J]. Power System Technology, 1998, 22(3): 24-28
[2] 李亚男, 张粒子, 杨以涵. 考虑电压约束裕度的无功优化及其内点解法[J]. 中国电机工程学报, 2001, 21(9): 1-4.
Li Yanan, Zhang Lizi, Yang Yihan. Reactive power optimization under voltage constraints margin[J].Proceedings of the CSEE, 2001, 21(9): 1-4.
[3] 许诺, 黄民翔. 原对偶内点法与定界法在无功优化中的应用[J]. 电力系统及其自动化学报, 2000, 12(3): 26-30.
Xu Nuo, Huang Minxiang. Application of primal-dual interior point method and branch-bound method in reactive power optimization[J]. Proceedings of the EPSA, 2000, 12(3): 26-30.
[4] 刘方, 颜伟. 基于遗传算法和内点法的无功优化混合策略[J]. 中国电机工程学报, 2005, 25(15): 67-72.
Liu Fang, Yan Wei. A hybrid strategy based on GA and IPM for optimal reactive power flow[J]. Procee dings of the CSEE, 2005, 25(15): 67-72.
[5] 潘珂, 韩学山, 孟祥星. 无功优化内点法中非线性方程组求解规律研究[J]. 电网技术, 2006, 30(19):59-65.
Pan Ke, Han Xueshan, Meng Xiangxing. Solution prin-ciples study of nonlinear correction equations in primal-dual interior point method for reactive power optimization[J]. Power System Technology, 2006, 30(19): 59-65.
[6] Suzuki M, Morima E. Coordinated A VQC operations of EHV transformer’s tap changer by fuzzy expert control system[A]. In: 2002 International Conference on Power System Technology[C]. 2002, 1679-1684.
[7] 阎振坤, 厉吉文, 李晓华. 基于模糊边界和双九区图的变电站电压无功控制策略研究[J]. 继电器, 2005, 33(10): 36-40.
Yan Zhenkun, Li Jiwen, Li Xiaohua. Study of voltage and reactive power integrative control strategy based on fuzzy boundary and double nine-area control method[J]. RELAY, 2005, 33(10): 36-40.
[8] 罗毅, 涂光瑜, 金燕云, 等. 基于多区图控制策略的地区电网电压无功优化控制[J]. 继电器, 2004, 32(5): 44-48.
Luo Yi, Tu Guangyu, Jin Yanyun, et al. Control over optimization of voltage and reactive power in regional power network based on multi-region chart control strategy[J]. RELAY, 2004, 32(5): 44-48.
[9] 余涛, 周斌. 电力系统电压/无功控制策略研究综述[J]. 继电器, 2008, 36(6): 79-85.
Yu Tao, Zhou Bin. A survey on voltage/reactive power control strategy for power systems[J]. RELAY, 2008, 36(6): 79-85.
[10] Yu T, Zhen W G. A reinforcement learning approach to power system stabilizer[A]. In: Proceedings of the 9th IEEE PES Power & Energy Society General Meeting[C]. 2009: 1-5.
[11] 胡细兵. 基于强化学习算法的最优潮流研究[D]. 广州: 华南理工大学, 2011.
[12] 袁野. 基于强化学习算法的互联电网AGC随机最优控制[D]. 广州: 华南理工大学, 2011.
[13] Vlachogiannis J G, Hatziargyriou N D. Reinforcement learning for reactive power control[J]. IEEE Transactions on Power Systems, 2004, 19(3): 1317-1325.
[14] Kaelbling L P, Littman M L, Moore A W. Reinforcement learning: A survey[J]. Journal of Artificial Intelligence Research, 1996: 237-285.
[15] 虞靖靓. 基于Q学习的Agent智能决策的研究与实现[D]. 合肥: 合肥工业大学, 2005.
[16] 余涛, 周斌, 陈家荣. 基于Q学习的互联电网动态最优CPS控制[J]. 中国电机工程学报, 2009, (19): 13-19.
Yu Tao, Zhou Bin, Chen Jiarong. Q-learning based dynamic optimal CPS control methodology for interconnected power systems[J]. Proceedings of CSEE, 2009, (19): 13-19.
[17] Bertsekas D P, Bertsekas D P. Dynamic programming and optimal control[M]. Belmont, MA: Athena Scientific, 1995.
[18] 杜春侠, 高云, 张文. 多智能体系统中具有先验知识的Q学习算法[J]. 清华大学学报: 自然科学版, 2005, (7): 981-984.
Du Chunxia, Gao Yun, Zhang Wen. Q-learning with prior knowledge in multi-agent systems[J]. Journal of Tsinghua University (Science and Technology), 2005, (7): 981-984.
Reactive power and voltage optimization control approach of the regional power grid based on reinforcement learning theory
Diao Haoran1Yang Ming1Chen Fang2Sun Guozhong3
(1. Key Laboratory of Power System Intelligent Dispatch and Control (Shandong University) Ji’nan 250061 China 2. Automation and Electrical Engineering, University of Ji’nan Ji’nan 250061 China 3. State Grid Tangshan Electric Power Company Limited Tangshan 063000 China)
Based on reinforcement learning theory, this paper proposes a practical approach for reactive power and voltage optimization control in regional power grid. The approach uses Q-learning algorithm to learn continuously under interaction between the action policies and grid states, then gets Q value function corresponding to each state - action, and finally forms the optimal grid reactive power and voltage control strategies. The approach gets rid of the convergence problems that existing in traditional reactive power optimization methods for solving nonlinear mixed integer programming model, meanwhile, compared to the multi - zone diagram method, as the Q value function contains global response messages in the whole grid, thus we can comprehensively judge the interactions between each substation and coordinate to control the reactive power and voltage control equipments, then obtain the global optimal control strategies in the jurisdiction grid. The approach paper proposes improves the reactive power and voltage optimization control results. Through a test of an actual 220kV substation and its feeder system, the example demonstrates the effectiveness of the approach.
Power system, reactive power and voltage optimization control, reinforcement learning, Q-learning algorithm
TM711
刁浩然 男,1992年生,硕士研究生,研究方向为电力系统可靠性分析。
国家重点基础研究发展计划(973计划)(2013CB228205),国家自然科学基金(51007047, 51077087),山东省自然科学基金(ZR2014EEM022)山东大学基本科研业务费专项资金(2015JC028)资助项目。
2014-10-01
杨 明 男,1980年生,副教授,研究方向为电力系统运行与控制。(通信作者)
