基于改进的Franklin 法估算标准生成吉布斯自由能应用于水体有机污染物降解的应用研究
2015-04-14张永祥秦灿高维春王由好段智隆兰双双
张永祥,秦灿,高维春,王由好,段智隆,兰双双
(1.北京工业大学 建筑工程学院,北京100124;2.水质科学与水环境恢复工程北京市重点实验室,北京100124;3.长安大学 旱区地下水文与生态效应教育部重点实验室,陕西 西安 710054)
对于一个不确定能否发生的有机污染物降解化学方程,可通过计算方程的吉布斯自由能变化,判断反应能否发生,估计平衡常数,甚至可以预判反应产物,对有机污染物降解新方法的探索及降解机理的研究都具有指导意义。
获得各项物质的生成吉布斯自由能ΔfGθ的方法有:查阅化学手册,但是化学手册仍缺少很多有机物数据;通过实验测得[1],操作复杂、控制条件苛刻;通过对应状态法[2]、基团贡献法、量子化学[3]和统计热力学方法[4]等进行估算。其中基团贡献法发展较早,操作简单,适合计算有机物,具有相当的准确性。
本文采用改进的Franklin 法[5]进行估算并校正,将结果应用于水体中有机污染物处理的化学方程的判断。相对于Franklin 法和其它基团贡献法,改进的Franklin 法可计算温度范围变宽,适合计算芳烃类有机污染物,更适用于水处理领域。
1 改进的Franklin 法
Franklin 证实有机物的生成吉布斯自由能ΔfGθ可通过基团贡献法进行计算,但只能计算特定温度(0,298.15,400,500,600,800,1 000,1 200,1 500 K)下的生成吉布斯自由能ΔfGθ。改进的Franklin 法发现在300 ~600 K、600 ~1 500 K 这两个温度范围内,基团贡献与温度近似呈正比关系,因此引入公式(Ⅰ),计算所需温度下的基团贡献值。

公式(Ⅰ)与公式ΔG =ΔH-TΔS 极为相似,A表示焓变ΔH 的量纲,近似为298.15 K 时ΔH 值;B/100 表示熵变的量纲,近似为298.15 K 时ΔS 值。
同时,考虑到基团之间的相互影响,改进的Franklin 法公式如下:

式中,∑基团贡献表示一个有机物分子中所有构成基团的生成吉布斯自由能贡献之和。RTln δ 表示对分子对称性[6]的校正,δ 为对称数[7]。
1.1 基团贡献
改进的Franklin 法给出了300 ~600 K,600 ~1 500 K烷烃基团、烯烃基团、共轭烯烃基团、炔烃基团、芳烃基团的A、B 值[5]。表1 为本文涉及到的不同基团在300 ~600 K,600 ~1 500 K 的A、B 值。根据表中A、B 值可计算基团在所需温度下的生成吉布斯自由能贡献。
表2 为本文涉及到的含O、X(卤)、N、S 基团在300 ~600 K,600 ~1 500 K 的A、B 值[5]。
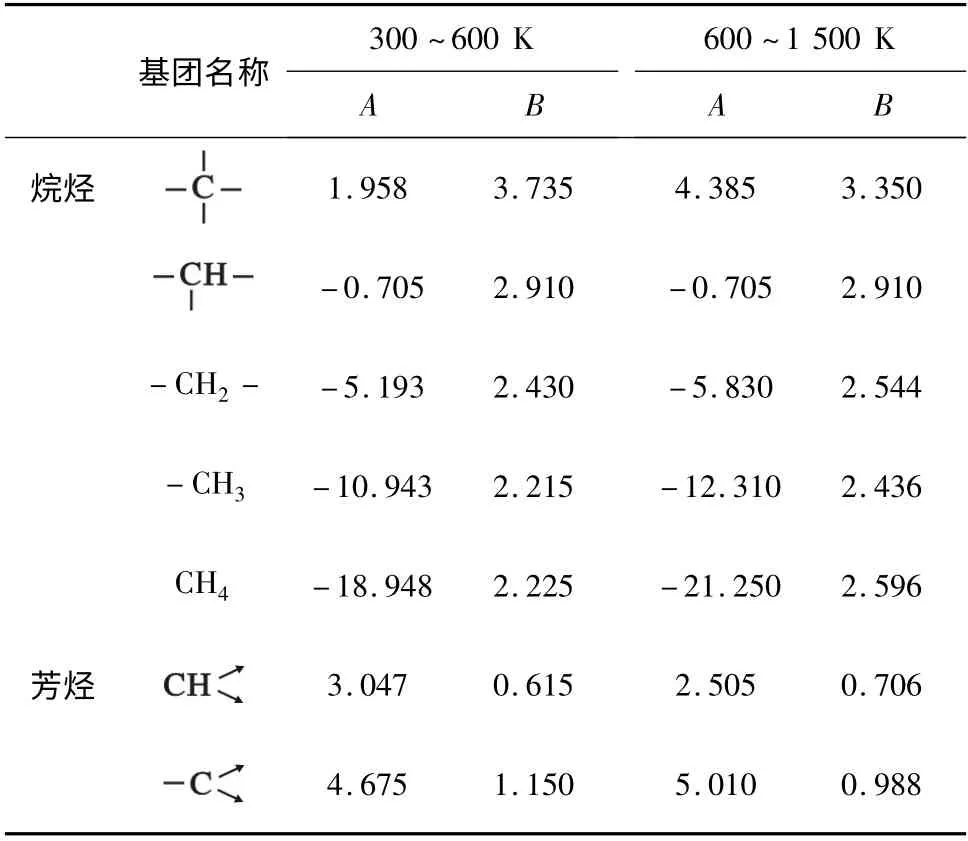
表1 基团的A、B 值Table 1 The A,B value of groups
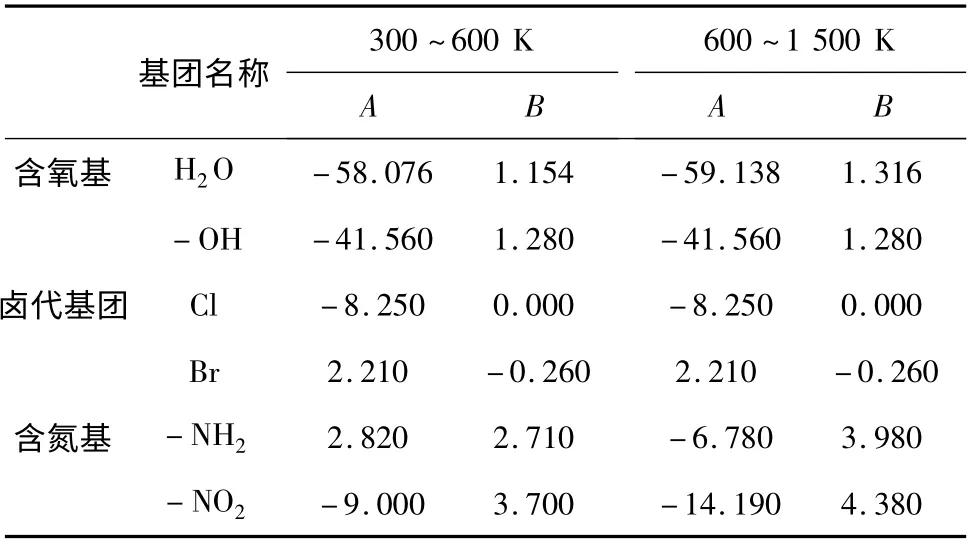
表2-O、-X、-N、-S 基团的A、B 值Table 2 The A,B value of-O,-X,-N,-S groups
1.2 基团贡献校正
根据改进的Franklin 法计算有机物的生成吉布斯自由能时,对于多环或分支结构的有机物需要进行基团贡献的校正[5]。芳烃环基团贡献的分支校正见表3。

表3 芳烃环的分支校正Table 3 The branch correction of aromatic ring
2 改进的Franklin 法计算水体常见有机污染物ΔfGθ
2.1 计算实例
水体中常见的有机污染物有苯系物、氯代苯类、多氯联苯、硝基苯类、苯胺类、酚类、挥发性卤代烃类。氯苯作为其中一种,具有致癌性、致突变性,为我国优先控制污染物。表4 以氯苯为例,计算在298.15 K 时的生成吉布斯自由能ΔfGθ。按照氯苯结构式,将氯苯拆分为5 个基团、一个基团、一个Cl,对称数δ=2,RTln δ=0.410。根据公式(Ⅱ)计算氯苯生成吉布斯自由能为103.21 kJ/mol。

表4 氯苯的ΔfGθ 计算过程Table 4 The ΔfGθ calculation process of chlorobenzene
2.2 水体常见有机物ΔfGθ 估算结果
水体中的有机污染物虽然含量甚微,但是有些极难被生物分解,对化学氧化和吸附也有阻抗作用,可以在水生生物、农作物和其他生物中迁移、转化和富集,并具有三致性[8],因此,水体中的有机污染物一直是水处理的热点。获得有机污染物的生成吉布斯自由能ΔfGθ,对水处理实验有一定的指导意义。通过查阅《兰氏化学手册》[9]、《有机化合物实验物性数据手册》[10]、《有机化学手册》[11]等专业化学手册,可得到部分有机污染物的ΔfGθ。表5 为常见有机污染物ΔfGθ的查阅值与改进的Franklin 法估算值。
由表5 可知,可查阅到ΔfGθ的有机物的估算值与查阅值基本一致:三氯乙烯TCE 估算值与查阅值相对误差最大,为39.95%;硝基苯相对误差最小,为0。苯系物相对误差均在10%以下,因为只有烷烃基和苯环构成。氯代苯类相对误差比苯系物略大,在10%左右,作者认为因为卤代基自身不稳定造成。苯胺类相对误差在20%左右,因为氨基不稳定。硝基苯类和酚类已知数据较少,已知值的相对误差在10%左右。以上数据说明改进的Franklin 法估算常见有机物的ΔfGθ值具有一定准确性,估算值可以被参考使用。作者对一些查阅不到ΔfGθ值但结构相近的有机物进行估算,结果见表5。
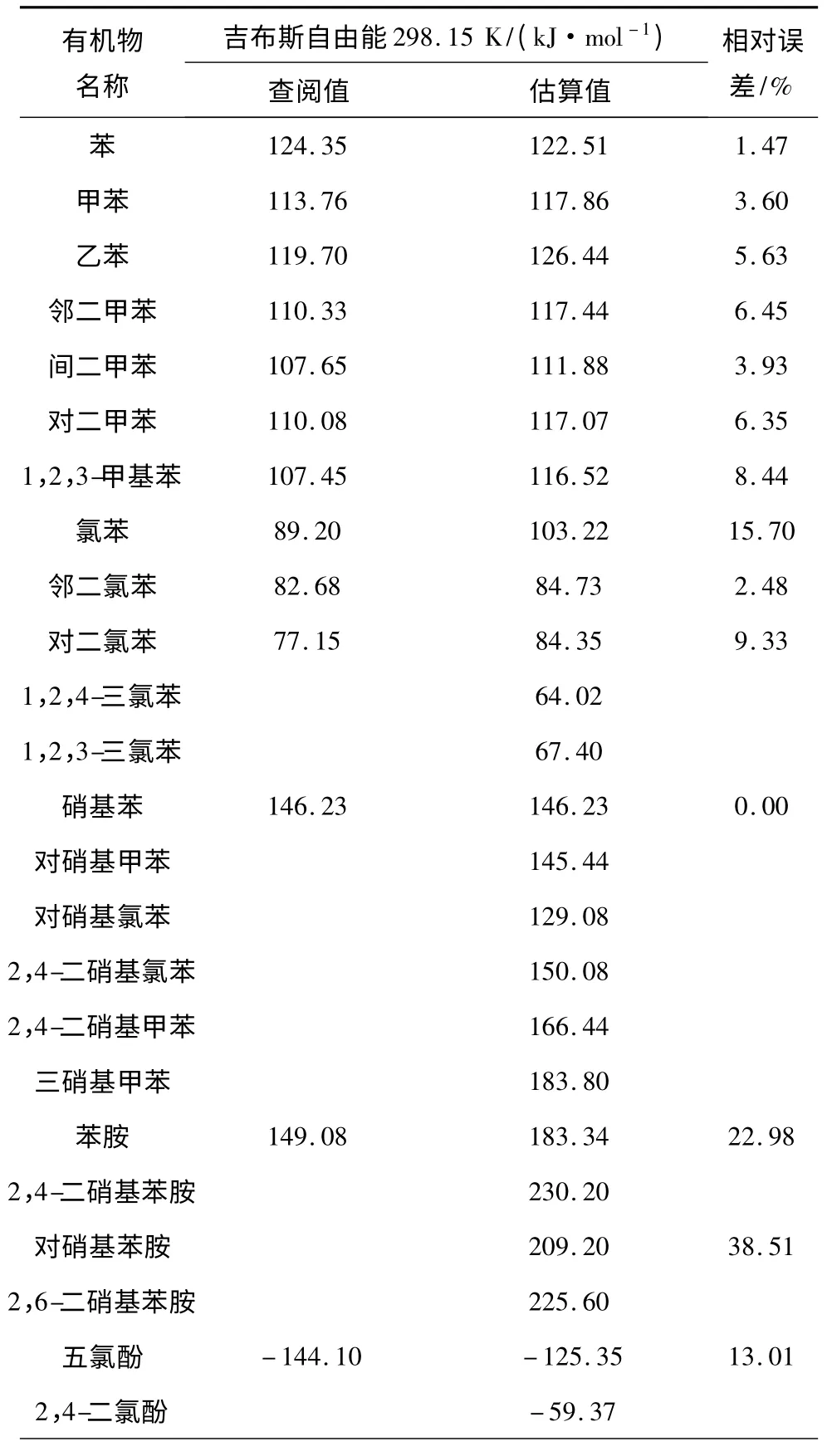
表5 常见有机物ΔfGθ 的查阅值与估算值Table 5 The ΔfGθ reference value and estimate value of common organic
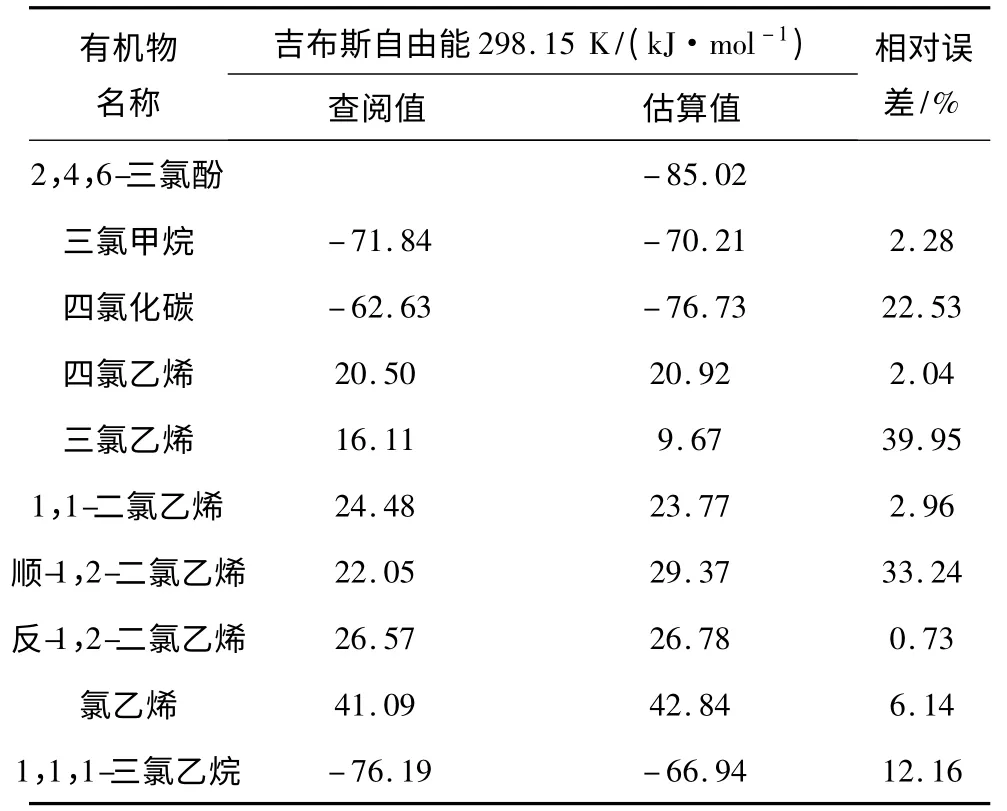
续表5
3 ΔfGθ 估算值在水处理中的应用
对于ΔfGθ值查阅不到的常见有机污染物,通过改进的Franklin 法估算其ΔfGθ值,估算值可以用来判断有机物降解反应可否发生,估算反应平衡常数,甚至可以预判反应产物,对水处理工作有一定指导作用。例如方程:

ΔrGθ<0 反应可正向进行。根据ΔrGθ=-RTln Kθ(Ⅳ)可获得标准状态下的平衡常数。
3.1 判断有机物降解反应可否发生
利用海藻酸钠包覆粗砂承载零价铁材料去除水中2,4-二氯酚[12]的降解机理为:

由于2,4-二氯酚生成吉布斯自由能查阅不到,常采用相似结构有机物的ΔfGθ值代替计算,为减少计算误差,现采用Franklin 法估算值计算,结果见表6。其他组分的生成吉布斯自由能为查阅值。
根据公式(Ⅲ)进行计算,该方程的生成吉布斯自由能变化ΔrGθ=-413.67 kJ/mol,ΔrGθ<0,反应可以发生。根据公式(Ⅳ)计算,反应平衡常数Kθ=1.18。

表6 方程(2)各组分ΔfGθ(kJ/mol)Table 6 The ΔfGθ of each component
3.2 判断反应生成物状态
改进的Franklin 法估算结果也可用于生成物状态判断。三氯甲烷去除机理[13]为:
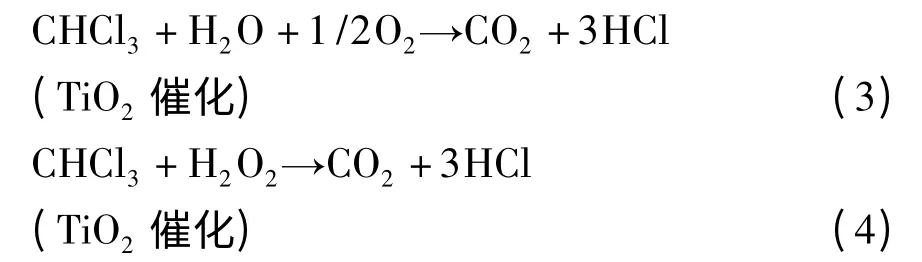
表7 为方程各组分的生成吉布斯自由能查阅值(kJ/mol),其中三氯甲烷为估算值。当CO2取气态值进行计算时,方程(3)ΔrGθ=308.19 kJ/mol,方程(4)ΔrGθ=191.37 kJ/mol。ΔrGθ>0 反应无法发生。当CO2取水溶液状态进行计算时,方程(3)ΔrGθ=-472. 92 kJ/mol,Kθ= 1. 210;方 程(4)ΔrGθ=-589.73 kJ/mol,Kθ=1. 268。通过以上计算结果可判断该反应生成的CO2以水溶液状态存在。

表7 方程(3)(4)各组分ΔfGθ(kJ/mol)Table 7 The ΔfGθ of each component
3.3 判断反应物降解程度
四氯乙烯(PCE)、三氯乙烯(TCE)、二氯乙烯(DCEs)、氯乙烯(VC)的去除机理[14-15]为:

表8 为方程各组分的生成吉布斯自由能查阅值,其中VC、PCE 为估算值,DCEs 取反-1,2-二氯乙烯的估算值进行计算(1,1,-二氯乙烯、顺-1,2-二氯乙烯计算结果相近)。

表8 方程(5)各组分ΔfGθ(kJ/mol)Table 8 The ΔfGθ of each component
根据公式(Ⅲ)按逐级降解进行计算,结果列于表9。
PCE、TCE、DCEs、VC 的ΔrGθ值逐渐增大,Kθ值逐渐减小。说明降解时PCE 反应最彻底。该计算结果与PCE 降解过程实验结果基本一致[16-17]。

表9 PCE 降解过程中ΔrGθ 计算Table 9 The ΔrGθ of PCE’s degradation process
[1] 董鹏丽,张梅,郭敏,等.Si2N2O 标准生成吉布斯自由能的测定[J].耐火材料,2012,46(3):169-173.
[2] 王莎莎,郭瓦力,田旭,等. 甲基异丙基酮制备3,4-二甲基吡唑的热力学计算与分析[J]. 当代化工,2012,41(1):98-102.
[3] Adrian Jinich,Dmitrij Rappoport,lan Dunn,et al.Qumantum chemical approach to estimating the thermodynamics of metabolic reactions[J/OL]. Scientific Reports(2014-11-12).www.nature.com/scientificreports.
[4] Bronneberg R,Pfenning A,Moquac.A new expression for the excess Gibbs energy based on molecular orientation[J].Fluid Phase Equilibria,2013,338:63-67.
[5] vanKrevelen D W,Chermin H A G.Estimation of the free enthalpy(Gibbs free energy)of formation of organic compounds from group contributions[J]. Chemical Engineering Science,1951,1(2):66-80.
[6] 周公度.化学辞典[M].北京:化学工业出版社,2011:190.
[7] Herzberg G. Infrared and Raman Spectra of Polyatomic Molecules[M].New York:Nostrand,1945:1-11.
[8] 王晓燕,尚伟. 水体有毒有机污染物的危害及优先控制污染物[J].首都师范大学学报,2002,23(3):73-78.
[9] James G Speight.Lange’s Handbook of Chemistry[M].16th Edition.New York:McGraw-Hill,2005.
[10]马沛生.有机化合物实验物性数据手册[M].北京:化学工业出版社,2006:465-528.
[11]George W Gokel.有机化学手册[M].北京:化学工业出版社,2006:459-499.
[12]胡筱.零价铁去除地下水中2,4-二氯酚系统的化学行为研究[D].北京:北京工业大学,2014.
[13]邵青,谭靖,吴维.零价铁/ TiO2去除水中三氯甲烷的实验研究[J].环境科学与技术,2009,32(11):91-94.
[14]Clayton J Clark,Rao P S C,Michael D Annable.Degradation of perchloroethylene in cosolvent solutions by zerovalent iron[J]. Journal of Hazardous Materials,2003,B96:65-87.
[15]Ma Changwen,Wu Yanqing. Dechlorination of perchloroethylene using zero-valentmatal and microbial community[J].Environ Geol,2008,55:47-54.
[16]刘菲,汤鸣皋,何晓娟,等. 零价铁降解水中氯代烃的实验室研究[J]. 地球科学-中国地质大学学报,2001,27(2):186-188.
[17]Arnold W A,Roberts A L.Pathways and kinetics of chlorinated ethylene and chlorinated acetylene reaction with Fe (0)particles[J]. Environ Sci Technol,2000,34:1794-1805.
