基于夹点方法和遗传算法的换热网络综合研究
2015-04-13韩保生马爱武
韩保生 马爱武 王 雷
(河南省锅炉压力容器安全检测研究院安阳分院 安阳 455000)
遗传算法对换热网络的求解过程中,往往要处理大量非可行解,效率低,且易陷入局部最优解中。本文将夹点方法和遗传算法相结合,利用夹点方法把网络分为夹点上下两个子网络区域,及对各决策变量和目标值的预估计,在一定程度上为遗传算法排除了大量非可行解,对寻得全局最优解提供了有力的指引。
1 最优夹点温差的确定
最优夹点温差是使换热网络年总费用最小的夹点温差,换热网络的综合,应在最优夹点温差下进行。换热网络年总费用包括公用工程费用、换热面积费用、换热器固定费用等。在不同的夹点温差下,综合出不同的换热网络,然后比较各网络费用,选取总费用最低的网络所对应的夹点温差。
2 换热网络模型
换热网络由NC个冷物流、NH个热物流和冷热公用工程组成。它们的初始温度、目标温度、热容流率、传热系数给定。综合的目的是确定各流股的匹配,使流股由初始温度达到目标温度,且网络年度总费用最小。本文采用Yee 等人的无分流的超结构模型:在超结构中换热网络级数NK=max(NC,NH),每一级中冷热流股之间串联匹配换热后,进到下一级,冷、热公用工程位于超结构两端。
2.1 约束方程
1)每个流股的热平衡
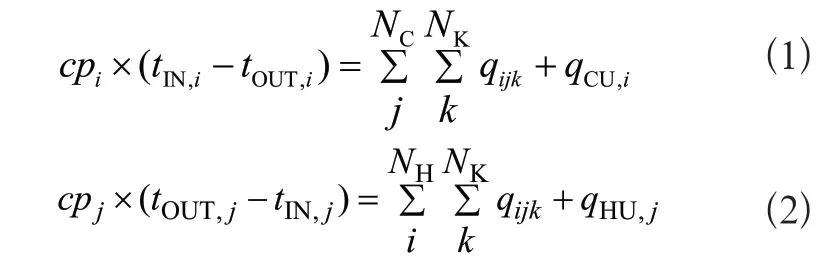
其中,下标i 为热流股序号,j 为冷流股序号,tIN表示进口温度,tOUT表示出口温度,CU 表示冷公用工程,HU 表示热公用工程。
2)每台换热器的热平衡

其中:下标MH 表示换热器热端,下标MC 表示换热器冷端。
3)温差约束
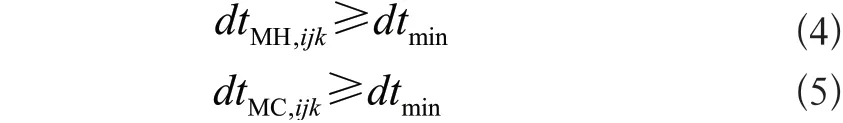
dtmin为最小传热温差。
4)温度约束
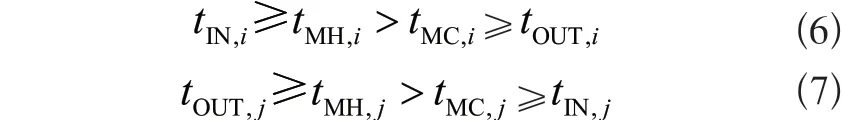
5)0-1 变量约束

1 表示换热器存在,0 表示换热器不存在。
6)夹点约束
夹点以下,不许加热公用工程,则
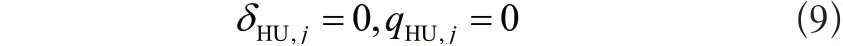
夹点以上,不许加冷公用工程,则
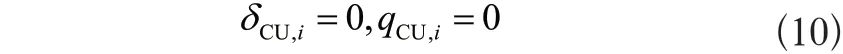
7)其他约束
连续变量(t,q)的非负约束;
若热物流i 必须与冷物流j 匹配,则 δijk= 1 ;若热物流i 禁止与冷物流j 匹配,则 δijk= 0 。
2.2 目标函数
为了换热网络的同步优化和费用权衡,取网络的年度费用最小为目标函数。目标函数如下:
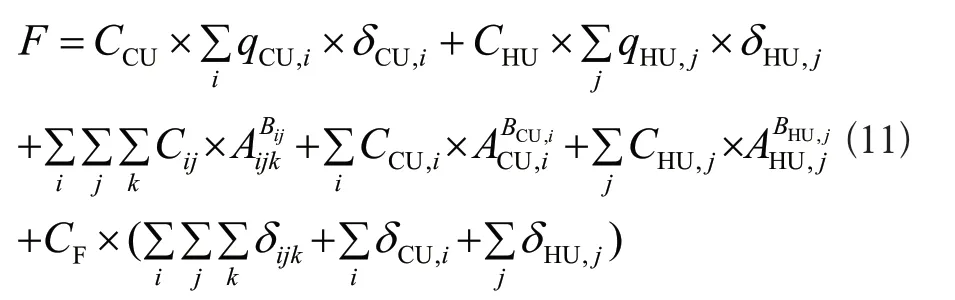
其中:C 为单位费用;B 为面积费用指数;A 为换热面积,由式求出;下标F 表示固定费用。
任何一个匹配,包括加热器和冷却器,换热面积按下式计算:
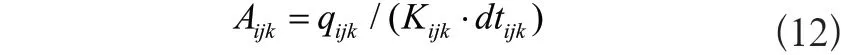
Kijk为热流股i 与冷流股j 之间的总传热系数;dtijk为对数平均温差。
3 遗传算法求解
遗传算法的基本原理[1]是:随机产生由若干个初始解组成的初始群体,利用适应度函数来评价个体解的优劣,决定当前群体中每个个体遗传到下一代群体中的机会多少。通过遗传算子对个体进行选择、交叉和变异,产生新个体,代替上一代适应度较差的个体传入下一代。重复此过程,直至满足一定条件为止。
利用夹点方法,在得到换热网络的最优夹点温差和夹点温度后,把网络分为夹点上下两个子网络。再利用遗传算法,以最优夹点温差为最小传热温差,分别对两个子网络进行搜索。夹点的确定,使得遗传算法在很大程度上避免了非可行解和提前陷入局部收敛的弊端。设计流程图如图1 所示。
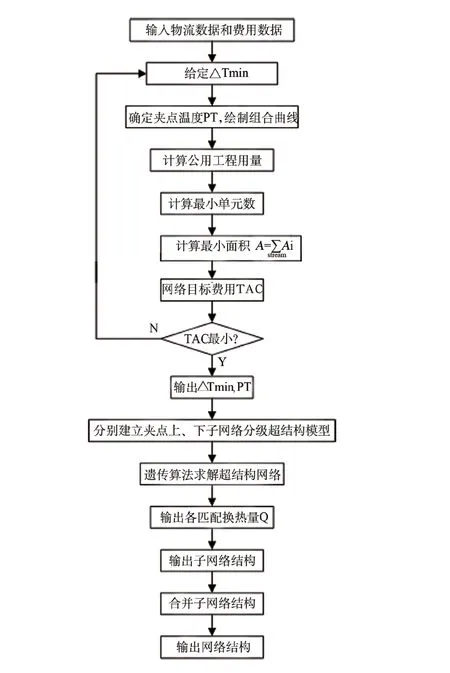
图1 换热网络优化设计流程图
4 初始可行解的产生
遗传算法中决策优化变量为各匹配的换热量qijk,采用十进制编码,一个个体维数为NH×NC×NK,群体大小为100。对每一个匹配qijk,取其最大允许的换热量fqijk。qijk的求解顺序为k=1,…,NK;i=1, …,NH;j=1,…,NC。
匹配最大值fqijk的确定可参考文献[2]。
5 算例
本例取自文献[3],数据见表1。
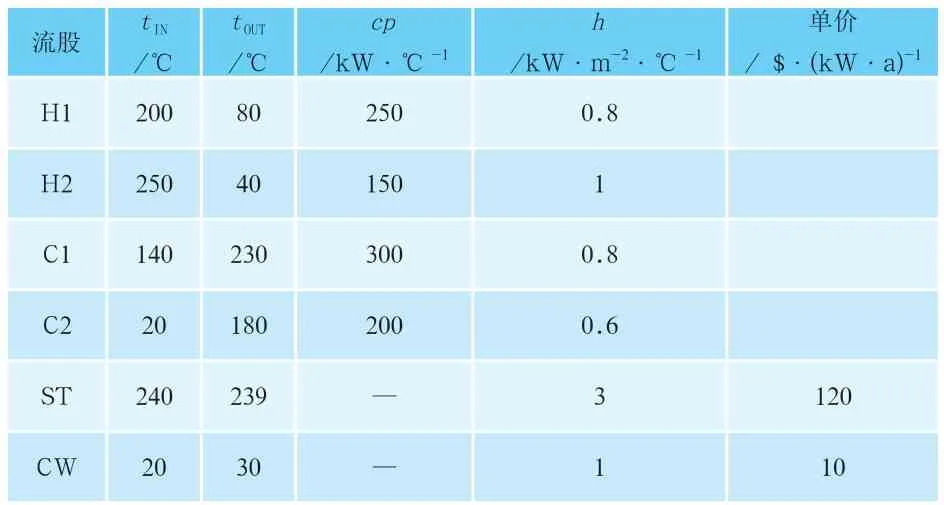
表1 算例的物流数据和费用数据
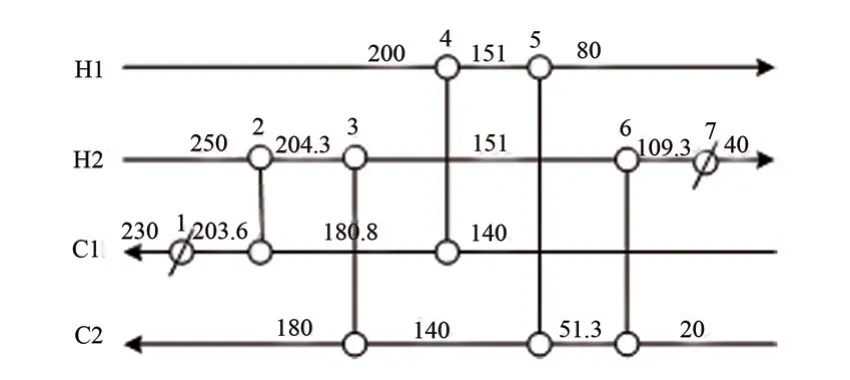
图2 网络结构
换热器面积费用取为500A $/a,固定费用为40000$/a。利用夹点方法得到最优夹点温差为11℃,夹点温度为145.5℃。利用遗传算法获得的换热网络结构如图2 所示。取交叉率为0.8,变异率为0.2,一代个体数目为100,在53 代找到最优解。网络总费用为4971350 $/a,比原文献费用降低了13650 $/a。
6 结论
1)结合夹点方法和遗传算法,对最小传热温差和网络结构参数进行分步优化;匹配换热量按顺序在可行范围内随机取值,从可行解中快速得到全局最优解。
2)计算实例表明了此方法的实用性和有效性。
[1] 雷英杰,等.遗传算法工具箱及应用[M].西安:西安电子科技大学,2005.
[2] 王克峰,尹洪超,袁一.遗传算法最优同步优化综合换热网络[J].大连理工大学学报,1997,1(11):62-67.
[3] Smith R.. Chemical process design and integration[M]. 2nd ed. UK: John Wiley & Sons Ltd,2005.
[4] Rezaei E., Shafiei S.. Heat exchanger networks retrofit by coupling genetic algorithm with NLP and ILP methods[J]. Computers and Chemical Engineering, 2009, 33:1451-1459.
[5] 魏关锋.用遗传/模拟退火算法进行具有多股流换热器的换热网络综合[D].大连:大连理工大学,2003.
[6] Yee T. F., Grossmann I. E.. Simultaneous optimization models for heat integration- Ⅱ. Heat exchanger network synthesis[J]. Computers and Chemical Engineering,1990,14(10):1165-1184.
