F2群体基因型数据带有误差时QTL的区间定位

佟 良，周 影，赵卫绩，丁 慧，邹大伟，李成凤，马春华

（1.绥化学院 信息工程学院，黑龙江 绥化152061；2.黑龙江大学 数学科学学院，黑龙江 哈尔滨150080）

数量性状位点（QTL）泛指影响数量性状的基因。将包含有遗传信息的染色体片段量化，使人们可以利用更多的统计手段来探求影响生物性状的QTL的数目、位置以及效应的大小，从而为遗传育种、疾病防治等工作提供支持。

分子标记被广泛应用到动植物的遗传研究中。Lander和 Botstein［1］，Zeng［2］，Kao［3］在这方面做出了突出贡献。但是上面所有方法都依赖于高精度的基因型测量技术，这一点由于基因型记分软件的某些缺陷以及生物化学的异常现象，所得到的基因型数据往往都带有一定测量误差。实际研究发现，即使是很小的基因型测量误差也会给遗传疾病的研究带来严重的负面影响，例如连锁分析（linkage analysis）研究和遗传距离的估计［4］以及连锁不平衡参数的估计［5］等。Lebrec等人［6］讨论了基因型误差对复杂性状连锁定位的影响。Hou等人［7］对QTL位于标记位点上的情况进行了分析，Tong［8］等人就回交群体给出了分析，但对F2群体没有做进一步的研究。

本文基于F2群体在基因型数据含有误差的情形下考虑了每个个体所有可能的基因型（基因图谱）。根据所有可能的基因型，在模型框架下给出了模型参数的估计方法。文中假设所有标记位点的基因型错误率相同，用EM 算法［9］和加权的EM 算法［10］进行参数模拟。研究表明，考虑F2群体基因型带有误差能够减少基因型误差给QTL定位带来的影响。

1 理论与方法

1.1 记号和背景知识

考虑N个自交个体，紧密连锁的M＋1个标记位点构成M个标记区间。假设标记位点均为两个等位基因Mj和mj，令

其中：Xij和˜Xij（i＝1，…，N，j＝1，…，M＋1）分别表示第i个个体，第j个标记位点真实基因型和含有误差的基因型。Yi表示第i个个体的表型值，X＊ij表示第i个个体，第j个标记位点内的潜在QTL基因型，令

令γj表示第j个标记区间两侧标记之间的重组率，γj1为第j个标记与第j个标记区间内的QTL之间的重组率，其中γj已知，假设一个标记区间内至多存在一个QTL，令p（）为第i个个体第j个标记区间基因型给定条件下的条件概率，它可由QTL位置以及QTL所在区间的双侧标记基因型计算求得。对于F2群体来说，其条件概率列于表1。

表1 F2群体标记基因型已知情况下QTL基因型的条件概率

假设每个标记位点的等位基因Mj和mj以概率为θ等可能被误编。这里θ＝p（＝k｜Xij≠k）表示基因型误差率（k＝－1，0，1），φi是第i个个体的联合误差率。ki表示M＋1个标记位点的错误编码个数，它是可以计算的。假定不同标记位点标记基因型是否有误差是相互独立的，可得到

式中：α为群体均值，βj为第j个标记区间内QTL的效应值，εi为随机误差，这里X＊ij与εi是相互独立的，且εi～N（0，σ2）。

1.2 基因型含有误差时模型参数的EM方法

模型的参数向量 Ω＝（α，β1…βM，γ，θ，σ2），其中γ＝（γ11…γM1）。由于观测到的基因型数据是含有误差的，因此，与通常的区间定位不同的是标记位点真实的基因型和QTL基因型均为潜在数据。这里采用EM算法进行参数估计。针对可能带有误差的标记基因型数据，借助前面的基因型图谱考虑每个个体所有可能的基因型；针对QTL基因型将依据相应的传递概率（见表1）对其补值。用标记位点真实的基因型和QTL基因型补全观测数据｛Yi），i＝1，…，N｝，进而得到完全数据｛，Yi，Xi，），i＝1，…，N｝。因而第i个个体的完全似然函数为

对于E 步来说，考虑到˜X，Y，Ω（k），计算lc（Ω）的条件概率，有

其中，Ω（k）为Ω当前的估计值，˜X＝（˜X1…˜XN）表示N个个体中含有误差的标记基因型，令

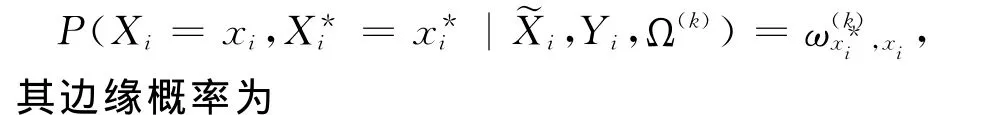
对于M 步来说，方程（1）的第1项只与α，β1，…，βM，σ2有关，第2项只与γ有关，最后1项只与θ有关，对于方程（1）的第1项，为了简单，考虑其矢量和矩阵形式。

令

E1可以通过下面公式推导求得

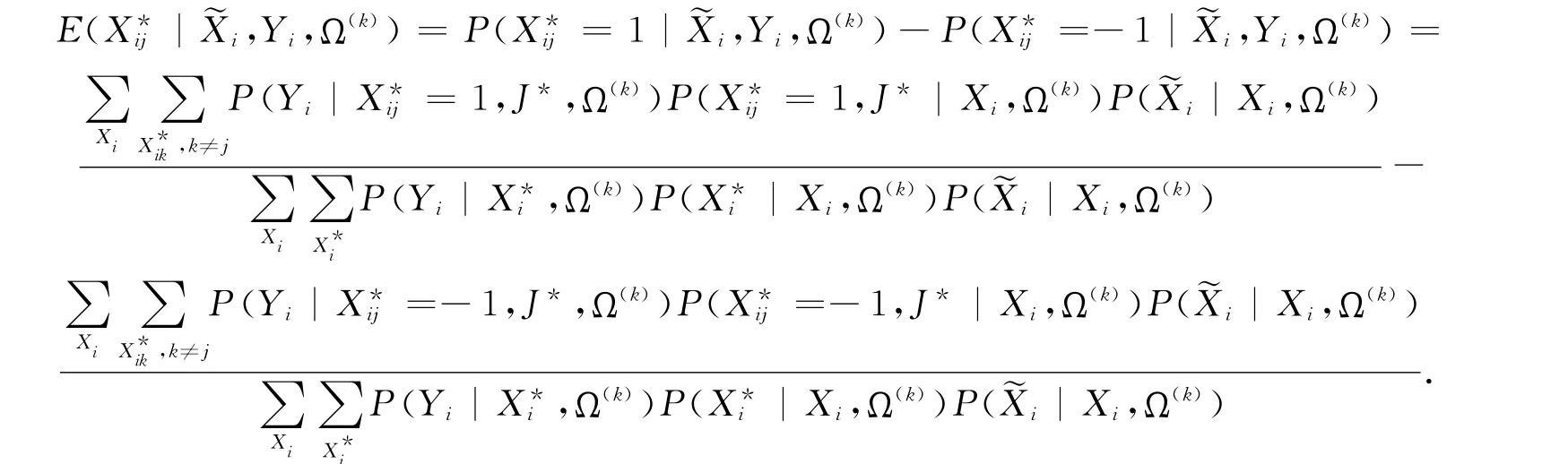
这里˜P＝P（˜Xc｜Xc，Ω（k）），，s，t＝1…M，k＝－1，1；l＝－1，1。

为了求得γ的迭代值，引入一个随机变量

对式（2）进行极大化，得到迭代公式

2 模拟与结果

模拟比较考虑基因型误差情形和不考虑基因型误差情形两种参数估计方法的好坏。为了简单起见，只考虑两个数量性状位点。标记密度对QTL效应的影响不大，同时，随着标记间距的减小，位置估计的准确性也有所提高，且趋向一致。所以只讨论标记间距为10cm的情况（标记间距可转化为重组率［12］），样本容量选定为500、1 000，两种方法的表型值＋εi，其中α是群体均值，εi～N（0，σ2）表示随机误差，，j＝1，2为QTL基因型的值，取值为－1，0，1。为了体现基因型误差θ，

2.1 模拟设计

重组率γ和QTL效应β1，β2之间的影响，在紧密连锁情形下模拟了θ＝0.00、0.01、0.05、0.10和γ11＝0.02，γ21＝0.03，参数β1，β2选取使得遗传力在0.05、0.1、0.2附近。对每个参数用本文提出的方法（记为PM）和不考虑标记位点误差的方法（记为QM）进行估计，并将整个过程重复500次来计算参数估计的均值。为了评价参数估计的偏性，给出了每个参数的均方误差（MSE）。

2.2 模拟结果

表2给出4种基因型误差率（0，0.01，0.05，0.1）和遗传力h2＝0.1情形下两种方法的参数估计值和MSE。容易看出，θ＝0时，所估计的参数值是等价的，这是合理的，因为这时条件期望E1，E2等于它们本身。θ≠0时随着基因型误差率的增加，两种方法的参数估计值逐渐偏离参数真值，但PM方法所估计的参数值更接近参数真值。这说明PM方法能够降低基因型误差率对参数估计的影响。同时看出，两种方法的MSE随着基因型误差率的增加而增加，但是PM方法的MSE小于QM方法的MSE，这再次表明考虑基因型误差能够降低测量误差带来的影响。

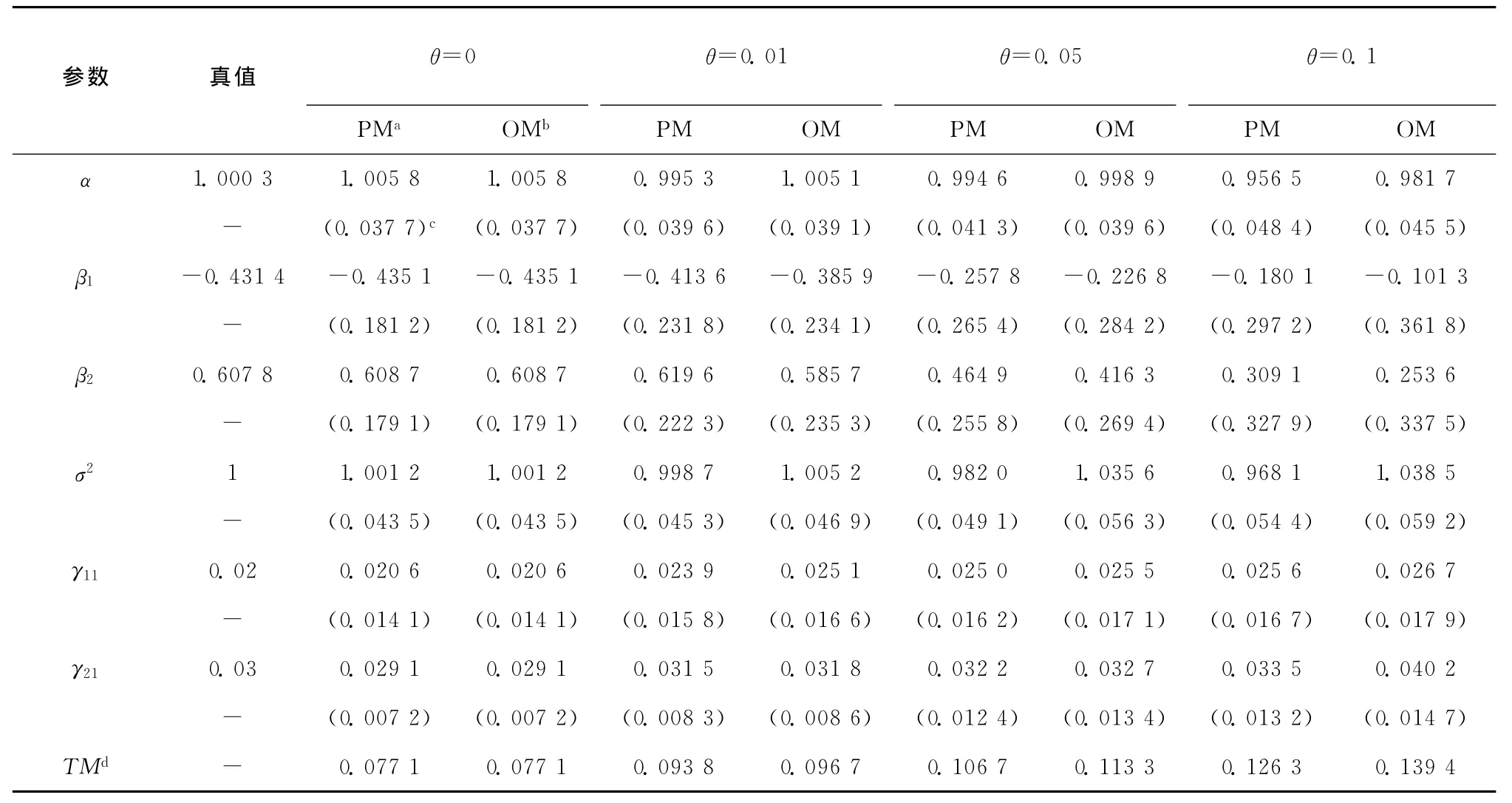
表2 样本量N＝500，h2＝0.1不同误差率情形下两种方法的模拟结果

PM方法能够估计误差率θ，表3给出遗传力N＝500，h2＝0.01、0.05、0.1时，误差率θ＝0的估计值，从表中可以看出，在遗传力和效应不同的条件下，误差率θ＝0.01的估计值随着θ＝0.05真值的增加，偏离程度逐渐增大，MSE随着基因型误差率的增加而增加。

表3 遗传力和QTL效应不同时误差率的估计

3 检验统计量

事实上，获得参数向量Ω的估计之后，可进一步讨论区间中是否显著存在QTL，用似然比统计量进行研究。原假设为区间内没有QTL，即

假设区间内至少有一个QTL，lc（Ω）表示对数似然函数，则相应的似然比统计量为

其中，＾Ω是在H1下Ω的 MLE，＾Ω0是在H0下Ω的MLE。通过简单的推导很容易求得Ω在H0和H1下的MLE。

4 结论与讨论

本文提出了基于F2群体基因型带有误差情形下区间定位的参数估计方法，模拟结果表明，新方法能较好地定位QTL位置，比不考虑基因型误差的方法更优。在相同条件下做样本容量为500，1 000的参数估计时，发现用于QTL定位的群体规模对QTL定位效果有明显的影响，随着群体规模的扩大，所有参数估计的准确度均随之提高。因此，在实际QTL定位中，让群体达到一定的规模，有助于提高QTL定位的可靠性，这与Jeon等人［13］的结论是一致的。对不同遗传力水平下QTL定位效果的分析表明，目标数量性状的遗传力高低对QTL定位的准确性也有明显的影响。当对高遗传力性状实施QTL定位时，QTL位置估计的准确性也相对较高。本文提出的方法可应用于误差率不同时QTL的区间定位。当误差率不同时，只需适当地调整基因图谱，同样可以得到各参数的迭代公式。

当然，本文提出的方法也存在不足之处。由于标记基因型带有误差和QTL基因型的未知性，当标记位点数目比较多时，算法中运算量会非常大。另外，EM算法也有自身的局限之处，它收敛速度较慢，并且收敛速度对初始值的选择有较大的依赖性。鉴于QTL多区间定位在基因病的研究中起到至关重要的作用，在未来的工作中对这类问题将会作进一步考虑，寻求更高效的算法，以便适应标记位点更多的情况。

［1］ LANDER E S，BOTSTEIN D B.Mapping mendelian factors underlying quantitative traits using RFLP linkage mals.Genetics，1989，121：185－199.

［2］ ZENG Z B.Precision mapping of quantitative trait loci.Genetics，1994，135：1457－1468.

［3］ KAO C H，ZENG Z B，TEASDALE R D.Multiple interval mapping for quantitative trait loci.Genetics，1999，152：1203－1216.

［4］ GOLDSTEIN D R，ZHAO H，SPEED T P.The effects of genotyping errors and interference on estimation of genetics distance.Hum Hered，1997，47：86－100.

［5］ AKEY J M，ZHANG K，XIONG M，et al.The effect that genotyping errors have on the robustness of common linkage disequilibrium measures.Am J Hun Genet，2001，68：1447－1456.

［6］ LEBREC J J，PUTTER H，HOUWING－DUISTERMAAT J J，et al.Influence of Genotyping Errors in Linkage Mapping for Complex Traits－An Analytic Study.BMC Genetics，2008，9：57.

［7］ HOU Y J，MA W J，ZHOU Y，et al.Parameter estimation in quantitative trait loci mapping when using data with genotyping errors.The Proceedings of 2010 International Conference on Probability and Statistics of the International Institute for General Systems Studies，2010，1：236－240.

［8］ TONG L，MA W J，ZHOU Y，et al.Simultaneous estimation of QTL effects and positions when using genotype data with errors.J.Genet.2015，94：27 –34.

［9］ DEMPSTER A P，LAIRD N M，RUBIN D B.Maximum likelihood from incomplete.data via the EM algorithm.Journal of the Royal Statistical.Society，Series B，1977，39（1）：1－38.

［10］IBRAHIM J G.Incomplete data in generalized linear models.J.Am.Statist.Association，1990，85（411）：765－769.

［11］MA W J，ZHOU Y，et al.A two－step method for estimating QTL effects and positions.Genet Res.，2011，93：115－124.

［12］周影，韩国牛，史宁中，等.约束下多子女家系数据重组率的最大似然估计［J］.中国科学：数学，2010，40（10）：971－984.

［13］JEON G J.The effects of population size and dominance of quatitative trait loci（QTL）on the detection of linkage between markers and QTL for livestock.AJAS，1995，8：651－655.