基于最优开通角的开关磁阻电机调速系统建模与仿真
2015-04-12张正苏
张正苏
(黑龙江工程学院 电气与信息工程学院,黑龙江 哈尔滨150050)
开关磁阻电机(SRM)是20世纪80年代中期随着电力电子技术、微型计算机技术和现代控制理论的迅猛发展而发展起来的一种新型机电一体化产品,是调速领域的一个新分支。与传统电机驱动系统相比,由SRM构成的驱动系统具有许多突出特点,主要包括:1)电机结构简单,定转子均为双凸极结构,不含磁钢,成本低;转子上无绕组,只在定子上装有简单的集中绕组,且绕组端部短,没有相间跨越,维护修理容易;2)其功率损耗主要发生在定子上,电机易于冷却,特别适合用于高速、高温、振动大等特殊场合[1-3]。功率电路简单可靠,SRM电机转矩方向只与各相通电顺序有关,与相电流方向无关,使各相绕组与功率开关器件可以采用串联方式,避免了两个功率器件直通的危险;电机各相绕组通电回路独立,旋转时可以缺相运行,容错能力强;能四象限运行,有较强的再生制动能力;低速性能好,无传统电机起动时出现的冲击电流现象[2-3];3)可控参数多,控制灵活,调速性能好,在宽广的速度和功率范围内都能保持较高效率。SRM电机效率高达88.3%,而通常的异步电机效率为85%。上述这些优点,使得SRM系统成为继交流异步电机、直流电机、永磁同步电机之后最有发展前景的驱动系统[4]。
本文以3kW,三相12/8极SRM为研究对象,应用Ansoft Maxwell有限元分析软件对开关磁阻电机进行仿真计算,获得开关磁阻电机的静态特性。在此基础上,进一步进行开关磁阻电机调速系统(SRD)建模,采用固定关断角并选取最优开通角的控制策略进行仿真分析。
1 SRM基本原理与数学方程
1.1 SRM基本原理
SRM的磁通是沿着磁阻最小的路径闭合,磁场的扭曲产生切向力使电机旋转起来。图1为SRM原理图。以αα′为轴线,一相绕组是由4个线圈连起来。电机的通电顺序与转子旋转方向相反,转子旋转方向与电流方向没有关系。在整个工作周期内,电机有时会存在两相同时通电的状态。
SRM样机结构为三相12/8极,每一相的全导通角度为15°。SRM在单相通电模式下(无提前开通角)会导致其在换相区间的转矩较小,意即在一相通电结束之后和下一相通电之初这段区间内,转矩相对较小,所以有转矩脉动的产生。常用的解决换相区转矩较小的问题就是在前一相通电结束之前使下一相提前导通,也就是在换相区间内两相同时通电,即加入提前开通角。

图1 SRM原理
1.2 SRM数学方程
电机的第k相电压平衡方程为
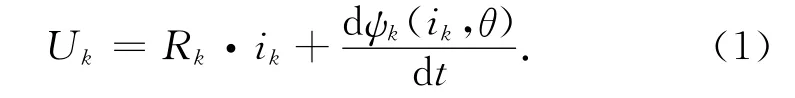
式中:Uk,ik,Rk,ψk(ik,θ)分别为第k相绕组两端的相电压、流经第k相绕组的相电流、第k相电阻和第k相磁链。
磁链可表示为


式中:Lk为第k相电感,ω为转子角速度,J为转动惯量,Tk为第k相的电磁转矩,TL为负载转矩,D为阻尼系数,k为电机相数。
2 SRM静态磁场计算
SRM样机结构参数为:定子(极对数6、外径120mm、内径69.5mm、极弧15°、轭厚12mm);转子(极对数4、外径68.5mm、内径30mm、极弧16.95°、轭厚 12mm);铁心长度 80mm、气隙0.3mm、绕组电阻为2.65Ω。
本文通过应用Ansoft Maxwell有限元分析软件分别对开关磁阻电机的磁场分布、电流-磁链-角度、电流-转矩-角度、电流-电感-角度等静态特性进行仿真和计算,图2为SRM样机结构。

图2 SRM样机结构
有限元的计算步骤如下:
1)创建模型:导入模型或在线设计模型。
2)对材料的属性进行定义。
3)边界的加载、激励的加载、网络的剖分和加载约束条件。
4)仿真模式设置,仿真计算。
经仿真分析可得其静态电磁特性如图3~图5所示。
3 SRD建模与最优开通角仿真分析
角度位置控制(APC)就是通过调节绕组供电的开通和关断来改变绕组电流的大小,从而改变转矩波形来实现控制,对于导通角的调节,开通角和关断角都可以进行调整,改变开通角可以调节绕组电流的幅域和有效值,改变关断角可以改变电流的宽度,进而影响电流的波形。开通角和关断角也可以影响临相的互感,进而影响其他相的电流波形。要使运行得到最优,要对每一相的开通角θon、关断角θoff都进行调节。
最优开通角的选取比较复杂,导通角是否最优主要取决于电流和转矩波形。转矩脉动最小,产生的负转矩也很小是衡量开通角是否最优的关键指标之一[7-9]。通常认为通过转矩对开通角求导,当转矩有效值最大时的开通角即为最优开通角,但其忽略了转矩脉动因素,转矩对开通角的求导不但计算繁琐而且对最优导通角选取也不一定准确,所以一般情况最优开通角选择都是通过寻优来获得的[5]。采用磁共能来计算开通角,当电流一定时,磁共能依赖开通角和关断角。去磁面积为充磁面积之差,充磁与关断角无关,去磁与开通角无关。寻找最优开通角就变成磁共能对其求导数的过程。图6为磁共能曲线。

图3 静态磁链特性曲线

图4 静态转矩特性曲线

图5 静态电感特性曲线

图6 磁共能曲线
开通角控制规律公式为[6]
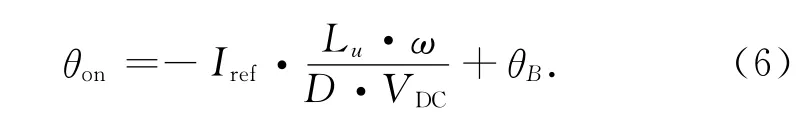
式中:Iref为参考电流,Lu为不对其位置的电感,D为经PI调节得到的电流。
以电机出力最大为原则,将关断角固定在某一位置,只调节开通角,若固定关断角太靠前,相电流将提前截止,出力减小,若固定关断角靠后,会产生负转矩,也就会影响总的出力。开通角的调节也要适中,开通角前移越多,则电流越大,开通角后移越多,会使主功率器件导通时间减少,影响相电流幅值大小,进而影响转矩和出力。
采用固定关断角调节开通角这种控制策略要考虑效率、转矩脉动和电机控制灵活简便等因素。
3.1 SRD建模仿真
SRD模型主要包含开关磁阻电机本体的模型、功率变换器的模型、控制策略模型和控制信号。开关磁阻电机本体的模型主要有磁链-电流-角度的函数模型或电感-电流-角度函数模型,功率变换器的模型主要是功率器件的开关,控制策略主要是PI、电流斩波控制策略、模糊控制策略和神经网络控制策略等,控制信号为给定的速度信号、负载转矩信号、转动惯量信号[10-12]。一相电机模型如图7所示。其包含电磁特性部分、转矩特性部分和机械特性部分。电磁特性部分和转矩特性部分都需要经过函数拟合计算。开关磁阻电机调速系统如图8所示,开关磁阻电机调速系统的仿真模型如图9所示。系统有两个闭环:外环速度环和内环电流环,速度环通过PI调节,电流环通过电流斩波控制。
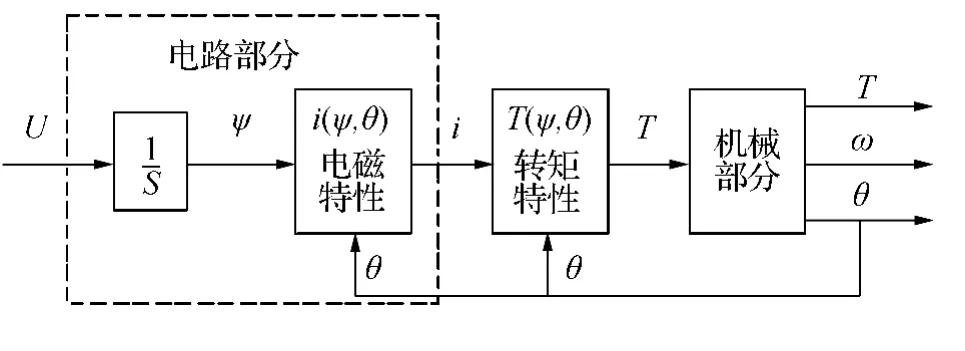
图7 一相电机模型
使用Matlab对样机进行仿真,电机的给定转速为3 000r/min,额定电压为514V,转动惯量为0.007 6kg·m2,摩擦系数为0.008N·m,负载为5.12N·m。电机由静止到转速为3 000r/min的全过程仿真波形如图10所示。
电机启动和低速的仿真波形如图11所示,可以看出在低速时采用电流斩波能够抑制启动时电流过大。

图8 开关磁阻电机调速系统

图9 开关磁阻电机调速系统的仿真模型
电机稳定在3 000r/min时的仿真波形如图12所示,此时采用电压斩波(CVC)控制。电机稳定运行时,波形保持相同,与常见的电机转矩、电流、磁链和位置波形相同。
3.2 最优开通角控制仿真
电机在转速为3 000r/min且负载为4N·m相同条件的情况下,以开关磁阻电机的B相为例,采用当前模型对电机进行角度位置控制(APC),本文采用固定关断角对开通角进行优化,最终选取三种导通模式进行仿真分析。第一种导通模式:开通角为13.1°,关断角为29°;第二种导通模式:开通角为15°,关断角为29°;第三种导通模式:开通角为17°,关断角为29°。三种导通方式的单相电流波形比较如图13所示。三种导通方式的单相转矩波形比较如图14所示。三种导通方式的合成转矩波形比较如图15所示。在此基础上对第一种导通模式额定负载5.12N·m进行仿真。图16为第一种导通模式下的位置和电流波形。从图中可以看出,仿真的一相电流相对于位置提前开通。
经分析可知:第一种导通模式相对于后两种导通模式在同样转矩和转速下其电流和转矩波形变宽,幅值变小,合成转矩脉动变小,是因为提前开通角增大,电机一相导通时间变长,所以电流变宽。因此,第一种导通模式对应的导通角就是最优导通角。通过仿真波形可以看出电流相对于转子位置提前开通,仿真的电流波形与实际的电流波形比较可以看出满足要求,同时验证了这种方法是可行的。

图10 电机运行(全程)仿真波形

图11 电机起动和低速运行仿真波形

图12 电机稳定运行(3 000r/min)仿真波形

图13 单相电流波形

图14 单相转矩波形

图15 三相合成转矩波形
4 结束语
开关磁阻电机的理论研究与工程应用始终是业界关注的热点,其中,作为相关理论应用验证的实验测试环节无疑是至关重要的,而针对开关磁阻电机调速系统(SRD)的建模与仿真正是实验测试前期的必备环节。本文采取固定关断角,通过确定最优开通角的控制策略进行系统仿真,通过设置不同模式进行仿真结果的观察并深入分析,发现相应转矩特性的规律,在有助于深化对SRM角度位置控制实现方法(APC)理解的同时,也为后续的SRD实验测试环节提供了数据预测基础。
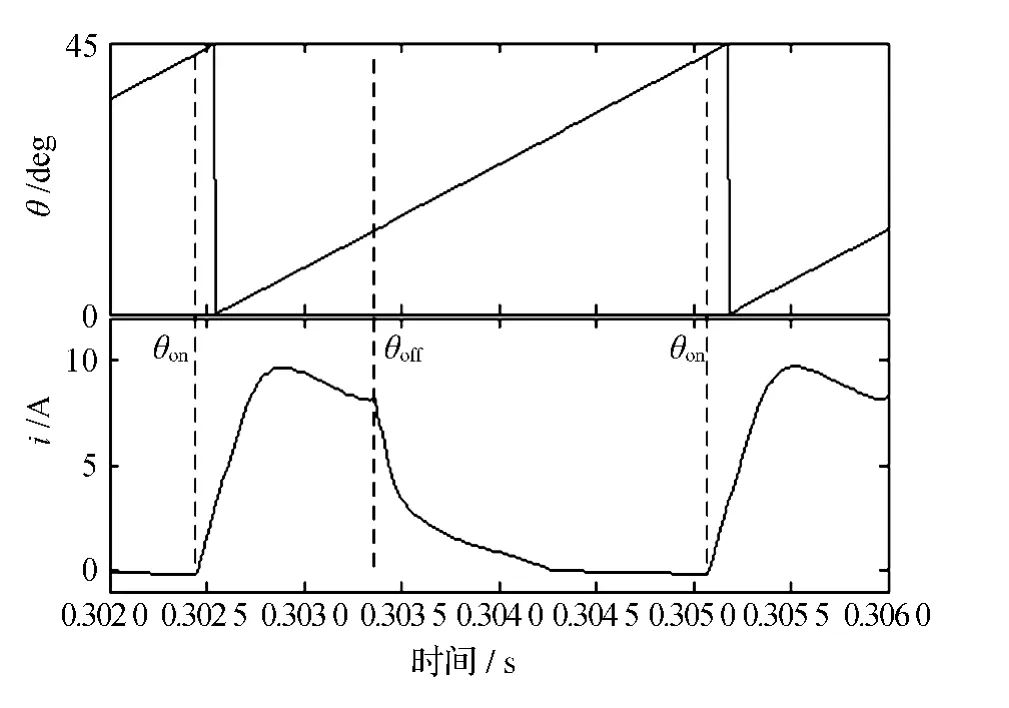
图16 导通模式1对应的位置和电流
[1] 吴红星.开关磁阻电机系统理论与控制技术[M].北京:中国电力出版社,2010.
[2] 吴建华.开关磁阻电机设计与应用[M].北京:机械工业出版社,2000.
[3] 吴红星,嵇恒,倪天,等.新型开关磁阻电机发展综述[J].微电机,2011,44(1):78-83.
[4] 王宏华.开关型磁阻电动机调速控制技术[M].北京:机械工业出版社,1995.
[5] 陈灵,黄运学,陈学.基于神经网络的SRM角度优化控制策略研究[J].电气传动,2011,41(3):46-50.
[6] AHN J W,PARK S J,LEE D H.Novel encoder for switching angle control of SRM[J].Industrial Electronics,IEEE Transactions on,2006,53(3):848-854.
[7] 王旭东.开关磁阻电动机开关角的在线最优控制[J].电机与控制学报,1999,3(4):211-214.
[8] 李景男,王旭东,周永勤.基于两相脉冲激励的开关磁阻电动机无位置传感器转子位置检测[J].电机与控制学报,2002,6(1):6-9.
[9] 王旭东,王喜莲.开关磁阻电动机电流双幅值斩波控制[J].中国电机工程学报,2000,20(4):83-86.
[10]边春元.开关磁阻电机驱动系统的理论和应用研究[D].沈阳:东北大学,2001:23-30.
[11]李晓艳.12/8极开关磁阻电动机调速系统的仿真分析与设计[D].哈尔滨:哈尔滨理工大学,2005:13-14.
[12]杨贵娟.基于DSP的开关磁阻电动机控制系统的研究[D].哈尔滨:哈尔滨理工大学,2009:10-12.
