太湖湖风指数阈值的计算

吕海龙，黄娟，王成林*，刘怡然，唐继顺

(1.解放军理工大学气象海洋学院，江苏 南京 210007；2.江苏省环境监测中心，江苏 南京 210036)



太湖湖风指数阈值的计算

吕海龙1，黄娟2，王成林1*，刘怡然1，唐继顺1

(1.解放军理工大学气象海洋学院，江苏 南京 210007；2.江苏省环境监测中心，江苏 南京 210036)

根据2012年8月17—23日的太湖湖风加密观测实验结果，将湖岸3个常规气象站和湖面2个浮标站观测的风速和气温资料代入经典的湖风指数公式，通过Fisher二级判别法和历史拟合率最大法确定了太湖湖风指数的阈值为3.0。该结论为研究太湖湖风的发生频率及其对蓝藻水华全湖输移的影响提供了理论依据。

太湖；湖风；湖风指数：阈值

0 引言

当前，太湖的水环境问题主要表现为蓝藻水华的大面积频发及其输移对饮用水源地水质安全的威胁。多数观点认同蓝藻水华的形成一般是由蓝藻本身的生理特点以及气象条件、营养盐、其他生物等诸多环境因素所引发的[1]。当太湖富营养化程度没有得到明显控制的情况下，气温较高、风速较小的气象条件适宜蓝藻生物单体的生长，并有利于其从水体上浮到表层，聚集形成水华[2-4]。这种气象条件同时也造成了较强的湖陆温差，相对于较弱的背景风场而言，此时湖风现象较明显，在湖面形成辐散风场[5-6]，这种风场必然改变水体流场形势，影响蓝藻水华的漂移路径，较长时间维持这种气象条件，往往出现大量的蓝藻在岸边或湖湾浅水区聚集。由此可见，夏季太湖出现大面积蓝藻水华现象时，常常伴有湖风现象发生。因此，在预测蓝藻水华漂移路径和聚集位置时，往往要考虑是否有湖风效应的影响。

随着观测资料的不断证实和湖风环流形成机理的逐渐清晰，为了利用尽可能少的观测资料判断和预测湖风的发生，各种指标和指数不断被提出和改进。1954年，HALL[7]是第一次提出芝加哥、伊利诺伊附近湖风的简单预测标准。这个标准包括：几乎碧空无云、微风和区域内有高压中心。BIGGS和GRAVES[8]应用尺度分析和相似理论研究发展了一种区分伊利湖西岸有无湖风现象的技术。他们的“湖风指数”如此定义：惯性力与浮力的比值，其中惯性力是由风速来计算，浮力是由湖陆温差来计算。LYONS[9]后来修改了他们定义的湖风指数，利用1966—1968年期间10个月中307 d的观测资料来分析确定芝加哥、伊利诺伊和格兰德、密歇根地区的湖风频率。ROEBBER[10]利用中尺度气象模式数值预报结果，结合BIGGS和GRAVES所定义的湖风指数对密歇根西岸的湖风进行了实时预测。LAIRD[11]根据BIGGS和GRAVES所定义的湖风指数，利用密歇根湖沿岸的地面观测资料分析了东岸和西岸从1982—1996年每年5—9月的湖风现象特征。但是，上述湖风指数阈值都是经验获得的，并不是通过严格的数学计算获得。

然而，至今没有相关研究开展太湖湖风指数及其判别阈值的计算。为此，笔者将根据观测事实，利用Fisher二级判别法和历史拟合率最大法确定太湖湖风指数的阈值。

1 数据与方法

1.1 观测数据介绍

2012年8月17日08时—23日05时开展了太湖湖风加密观测试验，获得56个时次湖面风场和大浦口岸边风廓线(图1中WP 01站点)。分析发现，其中10个时次湖面风场出现辐散特征，同时伴有垂直风切变，这表明观测期间共发生了10次湖风现象。将有湖风发生的情形记为事件A，没有湖风发生的情形记为事件B(表1)。

1.2 湖风指数的选择

由于湖风的水平尺度较小、垂直高度较低、形成至消亡过程的时间较短，其观测和数值模拟都较为困难。因此，利用水面和陆面有限的资料，通过湖风指数判断和预测湖风的发生被广泛应用。1962年，BIGGS与GRAVES利用尺度分析方法，提出了经典的湖风指数[8]：

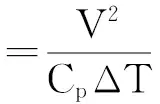
(1)

式中：Cp——干空气定压比热容，Cp=1.004J/(kg·K)；V——湖面风速；ΔT——湖岸地表气温和湖面水温的差。此后，很多学者采用了此指数公式研究湖陆风或是海陆风，但是这些研究在湖面风速V和湖陆温差ΔT的计算上各有不同，而且不同湖泊湖风指数σ的阈值也不相同[9-11]。

为了确定太湖湖风形成的阈值，对湖面风速V和湖陆温差ΔT的不同计算方法进行了一一检验，最终选择了湖面多个浮标站点风速平方的均值代表V2，选择湖岸多个站点地面气温与湖面多个浮标站水面气温的最大差值代表ΔT。为此，选择图1中BS01、BS03浮标站观测的湖面风速和气温，以及CS07(无锡站)、CS09(东山站)、CS19(湖州站)常规站观测的陆地气温，分别代入上述公式中，则：

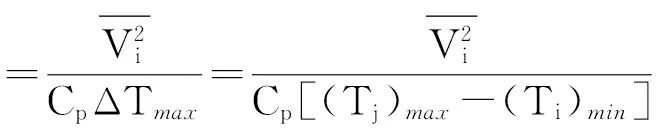
(2)

式中：Ti(i=1,2)——BS 01、BS 03浮标站观测的湖面气温；Vi(i=1,2)——BS 01、BS 03浮标站观测的湖面风速；Tj(j=1,2,3)——CS 07、CS 09、CS 19常规站观测的陆地气温。

2 太湖湖风指数阈值的计算

2.1 基本思路

(3)

Fisher二级判别的基本方法如下：

将湖风是否发生视为y，事件A与B的临界值设为yc，则判别函数：

yc=c1x1+c2x2

(4)

从而根据任一样本(x1,x2)可求出对应的y值，则对于任意y，有以下判别：

(5)

2.2c1，c2的计算

根据样本(x1,x2)的值(表1)，利用Fisher二级判别方法求出c1和c2：

则有：y=-0.001 6x1+0.004 8x2

(6)

此即为判别函数，据该式可求出每个样本的y值，见表1。

2.3 显著性检验

Fisher二级判别通常采用马氏距离构成F统计量检验，以此判别函数的显著性。构造方法如下：

(7)

图1 观测站点空间分布

(8)

(9)

式中：D2——马氏距离；m——样本总体分类数，在此取m=2。

A类和B类样本容量分别为nA=10、nB=46，则F=13.233 2。在信度α=0.05下，Fα(m,nA+nB-m-1)=Fα(2,53)=3.172。显然F>Fα,故判别函数显著。

2.4 yc的计算

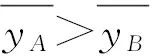
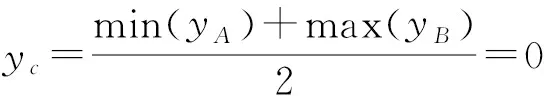
(10)

2.5 验证

依据新的判据yc=0.000 8≈0，判断56个样本的结果见表1。对比第5与第7列，可得出错判率为0。

另外，根据yc可以确定判别函数为：

0.000 8=-0.001 6x1+0.004 8x2

(11)

该式可近似转化为如下直线方程：

x1=3.0x2

(12)

在样本分布图中做出该判别直线，如图2所示，能够准确地区分两类事件。

2.6 总结

综上所述，可以近似确定σ的临界阈值为：

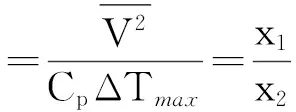
(13)

图2 太湖湖风指数阈值的确定

3 结论

在2012年8月17—23日连续1周的加密观测实验中，共观测得56组数据，其中共有10例湖风。为解决实际观测的诸多不便，采用BIGGS与GRAVES提出的经典湖风指数进行湖风判定。实际运用时，选取了湖岸3个常规气象站和湖面2个浮标站的风速和气温资料，利用Fisher二级判别法进行湖风指数阈值的计算。但由于有湖风现象与无湖风现象各自的样本容量相差较多， 采用通常的加权平均法求判据会造成较大误差，改用历史拟合率最大法，确定了太湖湖风指数的阈值为3.0，该结果通过了信度为0.05的F检验，同时，利用该指数及阈值对已有1周的观测数据进行回代检验，其结论与实际观测完全相符，即准确率为100%。据此结论分析长期连续观测的数据，就能发现太湖湖风发生的频率和持续时长等特征。

表1 Fisher判别法计算太湖湖风指数阈值

由此可见，当太湖湖风指数>3时，湖面风场往往不会出现明显辐散现象，湖面风场与周边岸基观测站测得的风场基本一致，此时可以不考虑湖风效应对蓝藻水华的输移；当湖风指数<3时，太湖湖面风场常常会出现明显辐散现象，湖面风场与周边岸基观测站测得的风场有明显差异，此时应考虑湖风效应对蓝藻水华的输移，不能简单地用岸基观测的风场来预警蓝藻水华的输移方向与聚集位置。

[1] 孔繁翔，高光.大型浅水富营养化湖泊中蓝藻水华形成机理的思考[J]. 生态学报, 2005，25(3):589-595.

[2] 王成林, 潘维玉，韩月琪，等.全球气候变化对太湖蓝藻水华发展演变的影响[J]. 中国环境科学, 2010，30(6):822-828.

[3] 吴晓东，孔繁翔.水华期间太湖梅梁湾微囊藻原位生长速率的测定[J]. 中国环境科学, 2008，28(6):552-555.

[4] 孙小静,秦伯强，朱广伟，等.风浪对太湖水体中胶体态营养盐和浮游植物的影响[J]. 环境科学, 2007(3).

[5] 王成林, 黄娟，钱新.高温微风条件下太湖流域风场时空特征分析[J]. 湖泊科学, 2011，23(1):122-128.

[6] 王成林,陈黎明，潘维玉，等.适宜太湖蓝藻水华形成的风场辐散特征及其形成机制[J]. 中国环境科学, 2010，30(9):1168-1176.

[7] HALL C.Forecasting the lake breeze and its effects on visibility at Chicago Midway airport[J]. Bull.Amer.Meteor.Soc.,1954，35:105-110.

[8] BIGGS W G，GRAVES M E. A lake breeze index[J]. Journal of Applied Meteorology, 1962(1):474-480.

[9] LYONS W A.The climatology and prediction of the Chicago lake breeze[J]. Journal of Applied Meteorology, 1972，11:1259-1270.

[10] ROEBBER P J，GEHRING M G.Real-time prediction of the lake breeze on the western shore of Lake Michigan[J]. Weather and Forecasting, 2000，15(3):298-312.

[11] LAIRD N F. Lake Michigan lake breezes:Climatology, local forcing, and synoptic environment[J]. Journal of Applied Meteorology, 2001，40(3):409-424.

[12] WILKS D S.Statistical methods in the atmospheric sciences[M]．Academic press,2011.

(栏目编辑 周立平)

Calculation on the Threshold of Taihu Lake Breeze Index

LU Hai-long1，HUANG Juan2，WANG Cheng-lin1*，LIU Yi-ran1，TANG Ji-shun1

(1.PLAUniversityofScienceandTechnology，Nanjing，Jiangsu210007，China；2.JiangsuEnvironmentalMonitoringCenter，Nanjing，Jiangsu210036，China)

Based on intensive observation results of Taihu Lake Breeze between August 17, 2012 and August 23, 2012, wind speed and temperature data from three conventional stations at shore and two buoy stations on lake was substituted into classic lake breeze index formula.By Fisher second level classification and history max-matching method, the threshold of Taihu Lake Breeze index was determined as 3.0. The conclusion provided a theoretical basis for the study on the frequency of lake breeze occurrence and its impact on the blue-green algae bloom transport in the whole lake.

Taihu Lake;Lake breeze;Lake breeze index;Threshold

2014-03-20；

2014-11-01

中国自然科学基金重点项目(41230421)；中国自然科学基金青年基金项目(41105075)；中国博士后基金项目(2013M532206)；中国江苏省自然科学基金面上项目(BK20131452)；中国人民解放军理工大学基础理论研究基金项目(KYQYZL001209)。

吕海龙(1991—)，男，本科，主要从事海洋气象研究工作。

*通讯作者：王成林 E-mail:chenglinwang@126.com

X524

A

1674-6732(2015)01-0010-05