汽车紧急避让情况下驾驶员心理负荷的研究*

刘英杰，赵又群，陈雪梅

(1.潍坊学院机电与车辆工程学院，潍坊 261061； 2.南京航空航天大学能源与动力学院，南京 210016；3.北京理工大学机械与车辆工程学院，北京 100081)



2015187

汽车紧急避让情况下驾驶员心理负荷的研究*

刘英杰1,2，赵又群2，陈雪梅3

(1.潍坊学院机电与车辆工程学院，潍坊 261061； 2.南京航空航天大学能源与动力学院，南京 210016；3.北京理工大学机械与车辆工程学院，北京 100081)

为从车辆行驶安全的角度出发，揭示紧急避让情况下驾驶员心理负荷的变化，利用动态心电分析仪、Frecord数据采集系统和动态GPS，进行紧急避让情况下驾驶员生理反应的试验。基于多元线性回归统计方法，对试验数据进行拟合，建立了同一车道上汽车距前方障碍物距离、汽车行驶速度、紧急制动时最大制动踏板速度、为避障而突然转向时最大转向盘角速度和驾驶员心率变化量之间的多元线性回归模型，对诸参数之间的关系进行了分析。结果表明，车距障碍物距离对最大转向盘角速度和最大制动踏板速度的影响大于汽车行驶速度的影响，且随着行车速度的增加和车距障碍物距离的减小，驾驶员心理负荷增大。

汽车；紧急避让；多元线性回归；驾驶员；心理负荷

前言

交通事故发生率居高不下，早已引起汽车行业的广泛关注。

驾驶员的行为被认为是从驾驶员感官信息到驾驶员操纵的映射，例如转向、制动或转向-制动相结合的操纵方式[1-4]。当遇到紧急情况时，驾驶员往往处于紧张状态，这时驾驶员的操纵准确性大为降低，严重影响车辆的行驶安全。通常情况下，车与障碍物之间的距离越近，车辆行驶速度越高，驾驶员操纵汽车的紧张程度就会越大。紧急情况下驾驶员准确的操纵行为对于保证交通安全具有重要意义[5-10]。

文献[11]和文献[12]中建立了包括车辆与障碍物之间的距离、车辆行驶速度、紧急情况下驾驶员生理反应变化量等因素的混合效应模型，分别对驾驶员转向行为和制动速度与生理反应间的关系进行了研究。

但在紧急避让情况下，驾驶员心理负荷与驾驶员转向行为和车辆制动速度是相互关联的。因此有必要对这三者之间的关系进行研究。

回归分析是现代应用统计学的一个重要分支，是研究事物间量变规律的一种科学方法。它研究一个因变量与一个或多个解释变量之间的相互依存关系，并估计或预测解释变量对因变量的影响，是研究变量之间非确定关系的多元统计分析方法。回归分析不仅能够分析解释变量对因变量影响的大小，还可以通过回归方程对因变量进行预测和控制[13]。

本文中基于多元线性回归分析方法，分别建立车辆紧急避让情况下最大转向盘角速度与车距障碍物距离和行车速度之间的线性回归模型、最大制动踏板速度与车距障碍物距离和行车速度之间的线性回归模型、驾驶员心理负荷与最大转向盘角速度和最大制动踏板速度之间的线性回归模型，并进行分析研究。

1 多元线性回归模型的基本理论

多元线性回归模型[14]为

y=Xβ+e

(1)

式中：y为n×1的观测向量；X为n×p的设计矩阵；β为未知参数向量；e为n×1随机误差向量。

参数向量β的估计值为

(2)

为了方便地进行模型的参数估计，通常对式(1)做如下假设。

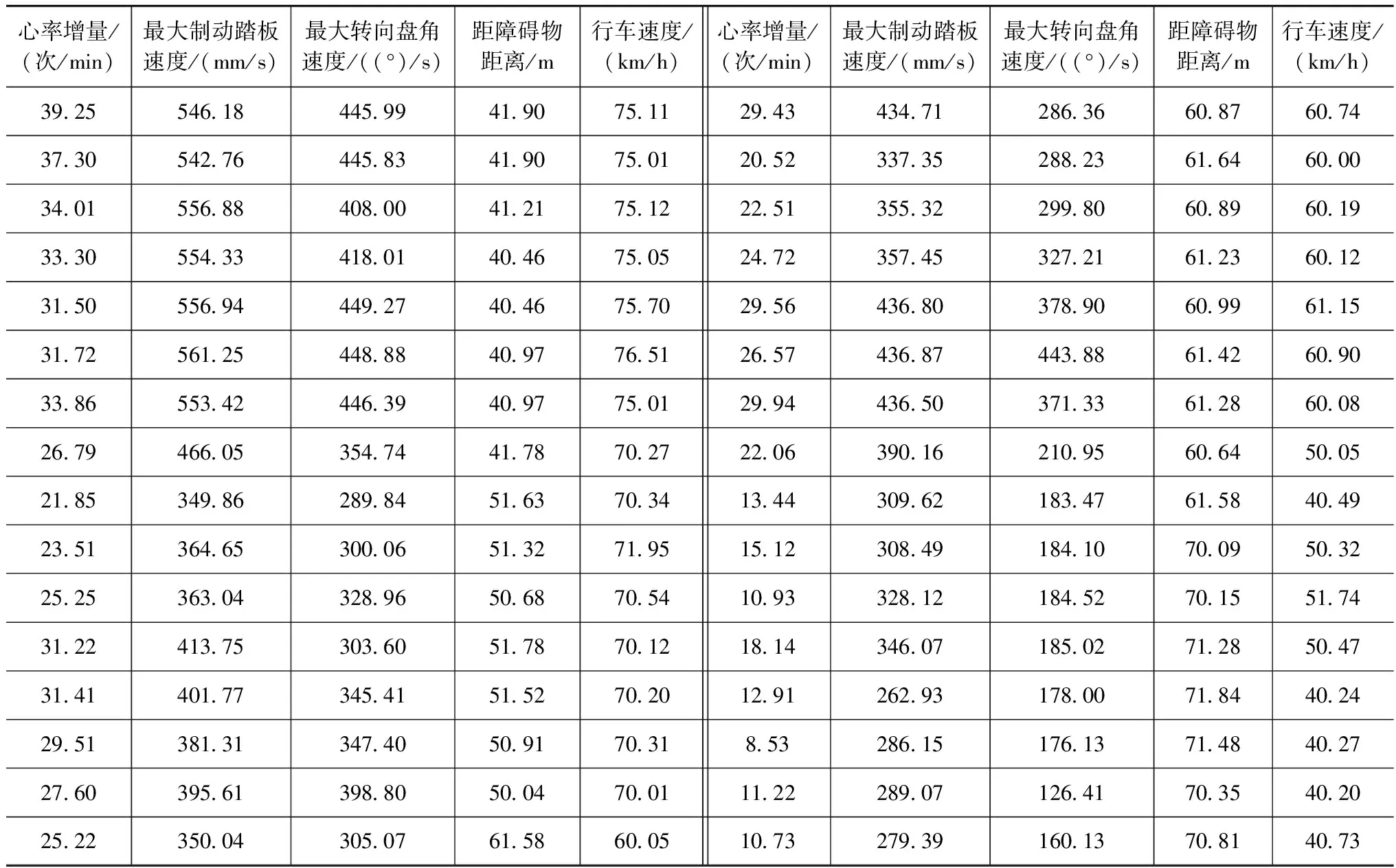
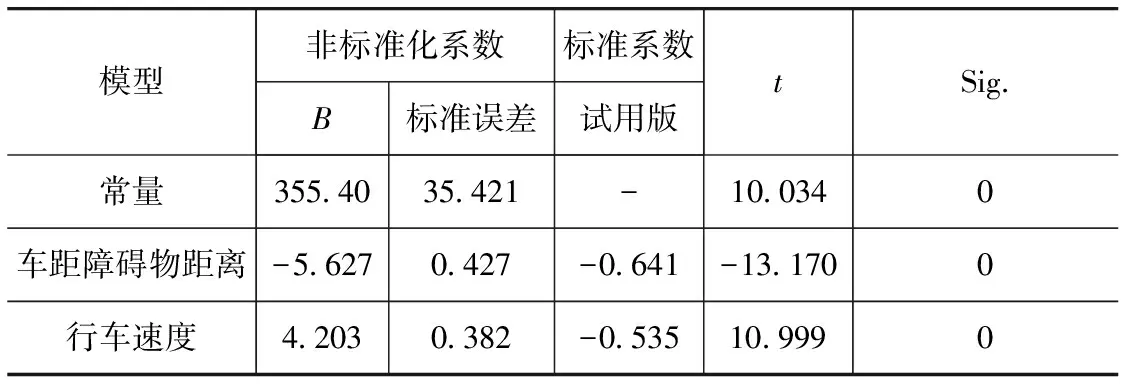
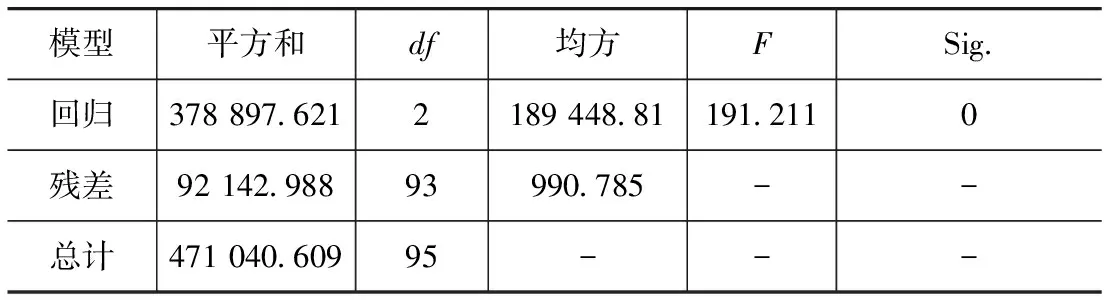
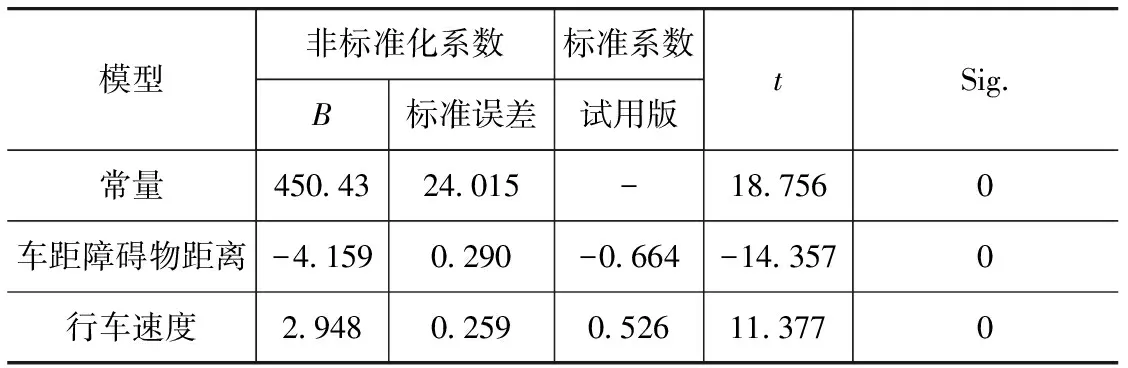
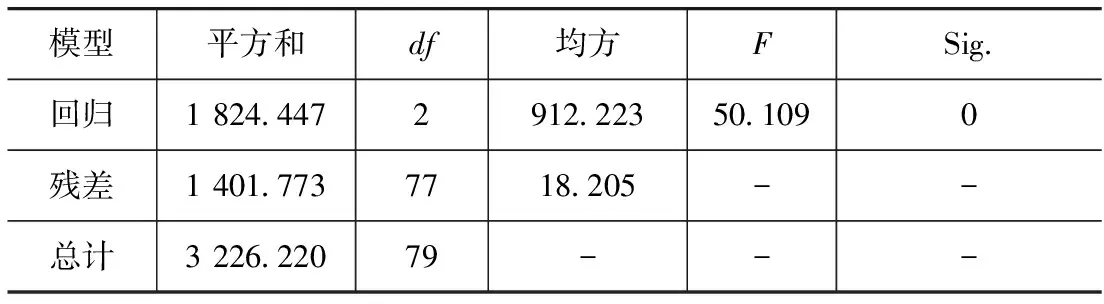
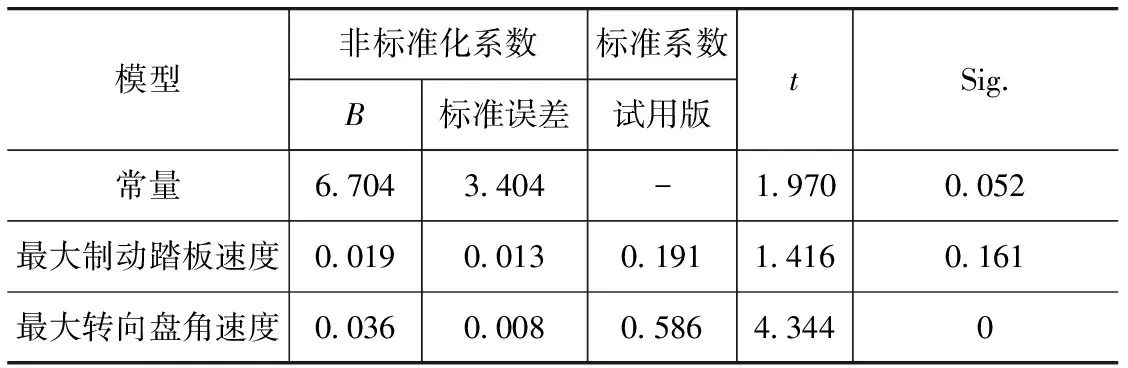
(1) 自变量x1,x2,…,xp是确定性变量，不是随机变量，且要求rank(X)=p+1

(2) 随机误差项具有0均值和等方差，即

(3)

式中：ei为对应的随机误差；σ2为方差。

(3) 正态分布的假定条件为

e～N(o,σ2In)

(4)

式中：o为零矩阵；In为n阶单位矩阵。

由以上假设和多元正态分布的性质可知，随机向量y遵从n维正态分布，即

y～N(Xβ,σ2In)

(5)

2 多元线性回归模型的建立

2.1 紧急避让试验设计

2.1.1 试验基本要求

研究路段要选择易于设置突发场景的路段；突发事件的设置要尽可能地逼近真实；障碍物的形状和状态要参考相应文献精心设计；测量车辆操纵指标要尽可能选用精度高的传感器，并要保证各个信号采集同步；要选择身体健康、反应正常和技术较熟练的驾驶员作为测试样本。

2.1.2 紧急避让试验方案

采用的道路如图1所示。在距长直路段与曲线路段衔接中点分别为40，50，60和70m的车道中心处放置固定障碍物，固定障碍物为长1m、宽0.5m和高1.5m的纸箱。由于直线路段与曲线路段的衔接点旁边种植很多树木，影响了驾驶员的视野，是产生突发场景的理想地点。设定初始行驶车速分别为40，50，60，70和75km/h。因为试验场地比较开阔，为制造突发场景采用试验人员与驾驶员聊天的方式人为干扰驾驶员的注意力获得突发状况。

2.2 试验数据的获取

选取8位有一定驾驶经验的驾驶员在紧急状况下进行驾驶行为试验，试验框图如图2所示。测量得到不同的车距障碍物之间的距离和车辆行驶速度条件下的驾驶员心率变化量、紧急制动时最大制动踏板速度和突然转向时最大转向盘角速度的变化，如表1所示[12,15]。

2.3 多元线性回归模型

2.3.1 最大转向盘角速度与车距障碍物距离和行车速度线性回归方程

分别绘制最大转向盘角速度与车距障碍物距离和最大转向盘转角与行车速度关系图，如图3和图4所示。由图可见，最大转向盘角速度与车距障碍物距离和最大转向盘转角与行车速度之间的关系近似为一条线性相关的直线，这说明采用多元线性回归方法进行定量分析是可行的。

表1 驾驶员心率增量、车距障碍物距离和车辆行驶速度部分试验数据

用统计分析软件SPSS进行分析。表2～表4分别为回归方程拟合度检验结果、方差分析结果和多元线性回归系数结果。

表2 最大转向盘角速度随行车速度和车距障碍物距离变化回归方程拟合度检验结果

表4 最大转向盘角速度随行车速度和车距障碍物距离变化多元线性回归系数结果

由表4可知，最大转向盘角速度变化量y1对自变量车距障碍物距离x11和行车速度x12的线性回归经验方程为

(6)

因式(6)为经验方程，故还须进行回归方程显著性的F检验和回归系数显著性的t检验。

当F>Fα(p,n-p-1)时，拒绝原假设，即认为在显著水平α下，y1对x11和x12有显著的线性关系，也即回归方程是显著的。也可以根据P值检验，表3中的Sig就是P值。P值与F值的关系为P(F>F值)=P值[13]，即F>167.974的概率为0，P值越小，F值越大；P值越大，F值越小。当P值<α时，回归方程是显著的，否则认为回归方程不显著。

利用表3中的Sig即P值，对回归系数x11和x12的显著性进行检验。它与t值的关系为P(|t|>|t值|)=P值。当P值≤α时，|t值|≥tα/2，此时认为该自变量与因变量之间有显著线性关系，否则，认为自变量的变化对因变量没有影响。

假设显著水平α=0.05，即认为“自变量全体对因变量y产生线性影响”这一结论错误的概率不超过5%。由上述分析及表3和表4的结果可知，最大转向盘角速度y1对自变量车距障碍物距离x11和行车速度x12的线性回归方程为

y1=355.40-5.627x11+4.203x12

(7)

由式(7)可以看出：在车距障碍物距离x11不变的情况下，行车速度x12增大，最大转向盘角速度随之呈直线关系增加，即驾驶员急于摆脱环境变化带来的危险，忙碌程度越大；在行车速度x12不变的情况下，车距障碍物距离x11增加，最大转向盘角速度随之呈直线关系减小，即驾驶员忙碌程度减小。并且可以看出，车距障碍物距离x11对最大转向盘角速度影响较大。

2.3.2 最大制动踏板速度与车距障碍物距离和行车速度线性回归方程

分别绘制最大制动踏板速度与车距障碍物距离和行车速度关系图，如图5和图6所示。由图可见，最大制动踏板速度与车距障碍物距离和行车速度之间的关系近似为一条线性相关的直线，因此可采用多元线性回归方法进行定量分析。

用统计分析软件SPSS进行分析。表5～表7分别为回归方程拟合度检验结果、方差分析结果和多元线性回归系数结果。

假设显著水平α=0.05。由表6和表7的结果可知，最大制动踏板速度变化量y2对自变量车距障碍物距离x21和行车速度x22的线性回归方程为

y2=450.43-4.159x21+2.948x22

(8)

表5 最大制动踏板速度随行车速度和车距障碍物距离变化回归方程拟合度检验结果

表6 最大制动踏板速度随行车速度和车距障碍物距离变化方差分析结果

表7 最大制动踏板速度随行车速度和车距障碍物距离变化多元线性回归系数结果

由式(8)可以看出：在车距障碍物距离x21不变的情况下，行车速度x22增大，最大制动踏板速度随之呈线性关系增加；在行车速度x22不变的情况下，增大车距障碍物距离x21，最大制动踏板速度随之呈线性关系减小。并且可以看出，车距障碍物距离x21对最大制动踏板速度影响较大。

2.3.3 心率变化量与最大制动踏板速度和最大转向盘角速度线性回归方程

分别绘制驾驶员心率变化量与最大制动踏板速度和最大转向盘角速度关系图，如图7和图8所示。由图7和图8可以看出，驾驶员心率变化量与紧急制动时的最大制动踏板速度和突然转向时的最大转向盘角速度之间的关系近似为一条正相关的直线，这说明可采用多元线性回归方法进行定量分析。

用统计分析软件SPSS进行分析。表8～表10分别为回归方程拟合度检验结果、方差分析结果和多元线性回归系数结果。

表8 心率变化量随最大制动踏板速度和最大转向盘角速度变化回归方程拟合度检验结果

表9 心率变化量随最大制动踏板速度和最大转向盘角速度变化方差分析结果

表10 心率变化量随最大制动踏板速度和最大转向盘角速度变化多元线性回归系数结果

假设显著水平α=0.05。由表9和表10的结果可知，心率变化量y对自变量最大制动踏板速度x1和最大转向盘角速度x2的线性回归方程为

y=6.704+0.019x1+0.036x2

(9)

由式(9)可以看出：在最大制动踏板速度x1不变的情况下，最大转向盘角速度x2增大，驾驶员心率变化量随之呈线性关系增加，即驾驶员心理负荷越大；在最大转向盘角速度x2不变的情况下，最大制动踏板速度x1增加，驾驶员心率变化量随之呈线性关系增加，亦即驾驶员心理负荷越大。并且可以看出，最大转向盘角速度x2对驾驶员心率变化量影响较大。

3 结论

(1) 在紧急避让情况下，制动踏板速度和转向盘角速度都反映出驾驶员心率即驾驶员心理负荷的变化。相对于最大制动踏板速度，最大转向盘角速度的变化对驾驶员的心理负荷影响作用较大。

(2) 一定行车速度条件下最大制动踏板速度和最大转向盘角速度与车距障碍物距离呈负相关的线性函数关系；一定车距障碍物距离条件下最大制动踏板速度和最大转向盘角速度与行车速度呈正相关的线性函数关系。

(3) 车距障碍物距离、行驶车速对转向盘角速度具有明显影响作用，且车距障碍物距离对转向盘角速度的影响作用大于行车速度对转向盘角速度的影响作用。

(4) 本文中提供的方法可以定量地分析紧急避让情况下驾驶员心理负荷与各影响因素之间的关系，也可为分析驾驶员对行车紧急程度的主观评价奠定基础。

[1] Morita K, Mashiko J, Okada T. A Study on Delay in Braking Operation when Drivers Looking Aside from Road Ahead[J]. Trans. Soc. Automotive Eng. Japan,2002,33(3):161-166.

[2] Takubo N, Fujioka T. Analysis of Glance Away in Driving[J]. Trans. Soc. Automotive Eng. Japan,2003,34(2):107-112.

[3] Lin C T, Wu R C, Liang S F, et al. EEG-based Drowsiness Estimation for Safety Driving Using Independent Component Analysis[J]. IEEE Transaction on Circuits and Systems,2005,52(12):2726-2738.

[4] José E Naranjo, Carlos González. Lane-Change Fuzzy Control in Autonomous Vehicles for the Overtaking Maneuver[J]. IEEE Transactions on Intelligent Transportation Systems,2008,9(3):438-450.

[5] Sun Li, Fang Liang, He Guoping. An Active Strategy Based on the Multiplier Function or the Gradient[J]. Application of Mathematics,2010,55(4):291-304.

[6] 李克强,王跃建,高峰.基于ITS的行车安全辅助系统[J].江苏大学学报,2005,26(4):294-297.

[7] 王昊.汽车视野安全的研究进展[J].江苏理工大学学报(自然科学版),2001,22(2):46-50.

[8] 刘英杰,赵又群,许健雄,等.基于Gauss伪谱法的紧急避让汽车操纵逆动力学[J].机械工程学报,2012,48(22):127-132.

[9] Chris L, Mohamed A A. Presence of Passengers: Does It Increase or Reduce Driver’s Crash Potential[J]. Accident Analysis and Prevention,2008,40(5):1703-1712.

[10] Jessica S, Jermakian. Crash Avoidance Potential of Four Large Truck Technologies[J]. Accident Analysis and Prevention,2012,49:338-346.

[11] 陈雪梅,魏中华,高利.驾驶员转向行为与生理反应的混合效应模型[J].北京工业大学学报,2009,35(2):230-234.

[12] 陈雪梅,高利,魏中华.紧急避障时驾驶员制动操纵特性研究[J].北京工业大学学报,2007,33(6):603-607.

[13] 刘顺忠.数理统计理论、方法、应用和软件计算[M].武汉:华中科技大学出版社,2005.

[14] 王松桂,陈敏,陈立萍.线性统计模型[M].北京:高等教育出版社,1999.

[15] 陈雪梅,魏中华,高利.驾驶员制动速度与生理反应的混合效应模型[J].江苏大学学报,2008,29(3):214-217.

A Research on Driver’s Psychological Burden Under theCondition of Vehicle Emergent Obstacle Avoidance

Liu Yingjie1,2, Zhao Youqun2& Chen Xuemei3

1.SchoolofMechanical-ElectronicandVehicleEngineering,WeifangUniversity,Weifang261061; 2.CollegeofEnergyandPowerEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016; 3.SchoolofMechanicalEngineering,BeijingInstituteofTechnology,Beijing100081

To reveal the change in driver’s psychological burden under the condition of emergent obstacle avoidance, starting from the angle of vehicle operation safety, tests on driver’s physiological responses under emergent obstacle avoidance are conducted by using Holter monitor, Frecord data collection system and dynamic GPS. Based on multivariate linear regression statistics, test data are fitted to get the multivariate linear regression models of driver’s heart rate variation against the distance between vehicle and front obstacles in the same lane, vehicle speeds, the maximum braking pedal velocity and the maximum steering wheel angular velocity with the relationships between parameters analyzed. The results indicate that the distance between vehicle and obstacle has larger effects on the maximum steering wheel angular velocity and the maximum braking pedal velocity than vehicle speed has, and the driver’s psychological burden increases with the rise in vehicle speed and the reduction in distance between vehicle and obstacle.

vehicle; emergent obstacle avoidance; multivariate linear regression; driver; psychological burden

*国家自然科学基金(11072106)资助。

原稿收到日期为2013年9月25日，修改稿收到日期为2014年4月17日。