Articial bee colony algorithm with comprehensive search mechanism for numerical optimization

Mudong Li,Hui Zhao,Xingwei Weng,and Hanqiao Huang

Department of Aeronautics and Astronautics Engineering,Air Force Engineering University,Xi’an 710038,China

Mudong Li*,Hui Zhao,Xingwei Weng,and Hanqiao Huang

Department of Aeronautics and Astronautics Engineering,Air Force Engineering University,Xi’an 710038,China

The articial bee colony(ABC)algorithm is a simple and effective global optimization algorithm which has been successfully applied in practical optimization problems of variouselds.However,the algorithm is still insufcient in balancing exploration and exploitation.To solve this problem,we put forward an improved algorithm with a comprehensive search mechanism. The search mechanism contains three main strategies.Firstly,the heuristic Gaussian search strategy composed of three different search equations is proposed for the employed bees,which fully utilizes and balances the exploration and exploitation of the three different search equations by introducing the selectivity probability Ps.Secondly,in order to improve the search accuracy,we propose the Gbest-guided neighborhood search strategy for onlooker bees to improve the exploitation performance of ABC.Thirdly,the selfadaptive population perturbation strategy for the current colony is used by random perturbation or Gaussian perturbation to enhance the diversity of the population.In addition,to improve the quality of the initial population,we introduce the chaotic oppositionbased learning method for initialization.The experimental results and Wilcoxon signed ranks test based on 27 benchmark functions show that the proposed algorithm,especially for solving high dimensional and complex function optimization problems,has a higher convergence speed and search precision than ABC and three other current ABC-based algorithms.

articial bee colony(ABC),function optimization, search strategy,population initialization,Wilcoxon signed ranks test.

1.Introduction

However,thereisstill muchinsufciencyoftheABCalgorithm about its solution search mechanism which brings a premature convergence and low search accuracy when solving complex multimodal problems and a poor convergence for handling unimodal problems[12].As we know, the search strategy of ABC performs better in exploration but weaker in exploitation[13].The‘exploration’and‘exploitation’[14]play the decisive role in the swarm intelligence optimization algorithm in terms of efciency and accuracy.Here,exploration means the ability of exploring different regions in the search space tond a better solution,while exploitation is the capacity of searching in a specic area in order to pick up a candidate solution.

Consequently,how can we keep a better exploration and improve exploitation of the search strategy for ABC becomes a key issue for current research.Scholars have put forward many strategies to improve the performance of the ABC algorithm for the problem.Rosenbrock’s rotational direction method was used in the exploitation phase of ABC in order to promise its convergence speed[15]. The Gbest-guidedsearch strategy was proposedas the new solution search equation of ABC to balance the ability to a certain extent in Gbest-guided ABC(GABC)[12].The neighborhoodsearch equation inspired by the behaviors of onlooker bees was put forward to improve the local search ability of the quick ABC(qABC)algorithm[16].Combining the differential evolution algorithm,namely differ-ential evolution(DE)[17]and ABC algorithm,the modied ABC(MABC)introduced the selective probability P to balance the exploration and exploitation of the solution equation[18].The above improved algorithms have enhanced different aspects of the performance for the ABC algorithm.However,it is difcult to make a better balance between both.

To solve this problem,we propose a comprehensive search mechanism for the ABC algorithm(CSABC).The search mechanism includes three strategies for different processes of ABC.Firstly,for the employed bees process, we introduce a selectivity probability Psto choose one of the three equations including the Gbest-guided search equation,optimal guidance equation and standard search equation of ABC,namely the heuristic Gaussian search strategy.This strategy is used to achieve the purpose of balancing the performance of the three different equations so as to utilize the exploration capability as well as improving the exploitation capability of ABC.Secondly,for the onlooker bees process,inspired by the neighborhood search method,we put forward the global optimal guided neighborhoodsearch equation so as to further improve the exploitation of the algorithm.This strategy uses the current best solution to control the search direction of onlooker bees in its neighborhood.Thereafter,for the current colony,the self-adaptive perturbation strategy which contains random perturbation and Gaussian perturbation is used to adjust the location around the colony slightly in order to avoid precocious phenomena appearing in the process of convergence.In addition,the chaos oppositionbased learning method is used for initialization to enhance the quality of the initial colony.

The rest of this paper is organized as follows.In Section 2,the ABC method is briey introduced.Section 3 describes the improvedABC algorithm in detail.Section 4 presents and discusses the experimental results based on 27 benchmark functions.Finally,Section 5 is devoted to conclusions and future work.

2.A brief introduction to ABC

In the ABC algorithm,the bee colony consists of three parts,namely employed bees,on looker bees and scout bees[1].The number of employed bees,which is half of the colony,is equal to that of onlooker bees.Each employed bee is associated with one food source,and the amount of food sources corresponds to the quality(tness) of the associated solution.The following is a list of major phases of the ABC algorithm.

At the beginning,the initial colony of solutions is generated by SN randomly generated D-dimensional realvalued vectors,namely food sources.Let Xm= {xm,1,xm,2,...,xm,D}represent the mth food source in the colony,and each food source is generated by theowing equation:

where m=1,2,...,SN,i=1,2,...,D.Liand Uiare the lower and upper bounds for the search space.Then evaluate and calculate thetness of each solution by(2), meanwhile record the global optimal value.

where fmis the target function of Xm.

Thereafter,each employed bee Xmgenerates a new food source Vmby(3)which we call standard food source search equation as follows:

where m,k∈{1,2,...,SN},k is a randomly chosen index meanwhile k/=m and i∈{1,2,...,D}.ϕm,iis a randomnumbergeneratedfromthe range[−1,1].Through calculating thetness values,better solutions are chosen by using a greedy selection mechanism.

Then each onlookerbee selects a foodsource Xmby its probability value pmas the following equation,and generates the modication on Xmby using(3).

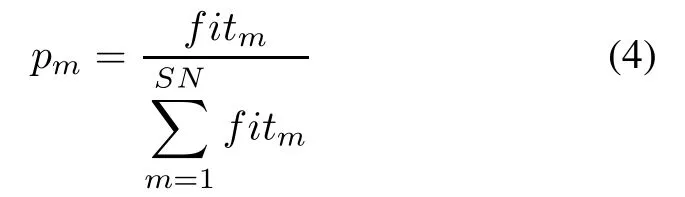
where fitmis thetness value of solution m.

Finally,forthescoutphase,ifasolutiondoesnotchange over a certain number(limit)of generations,the food source is to be abandoned and the associated employed bee becomes a scout.Then the scout bee produces a food source randomly by(1).

3.ABC with comprehensive search mechanism

3.1Initialization method

As an intelligent search algorithm based on the swarm optimization,ABC uses the method that randomly generates a food source to initialize the populationin the search range.The study found that the dispersion degree of the population initialization position in the search space has greateffectsontheperformanceofaswarmintelligencealgorithm in population diversity[19].The experience from different algorithms shows that the dispersion degree of this method needs to be further improved[20,21].Therefore,thechaossystem combinedwiththeopposition-based learning method was used for initialization in[18].In thispaper,we introduce the logistic mapping for producingthe chaos factor and apply it to the population initialization phase so as to improve the population quality.The algorithm for the initialization is described in Algorithm 1.

Algorithm 1Chaotic opposition-based learning method of initialization

01:Set the population size SN and chaotic iteration number M

//Logistic chaos phase//

02:form=1 to SNdo

03:fori=1 to Ddo

04: Randomly generate the initial chaos factor

ζj=1,i∈(0,1)

05:forj=1 to Mdo

06: ζj+1,i=4ζj,i(1−ζj,i)ζj,i

07:end for

08: xm,i=Li+ζj+1,i(Ui−Li)

09:end for

10:end for

//Opposition-based learning method//

11:form=1 to SNdo

12:fori=1 to Ddo

13: Oxm,i=Li+Ui−xm,i

14:end for

15:end for

3.2Heuristic Gaussian search strategy for employed bees

According to the standard search equation of ABC,the algorithm has strong ability of exploration because of random selection of the search equation,where the better or worse individuals have the same probabilityto be selected. However,the poor exploitation of ABC is also due to the search equation,leading to the problems of slow convergence speed and low search precision.Aiming at the insufciency,inspired by the search equation of PSO,the Gbest-guided search equation(5)was proposed in[13]:

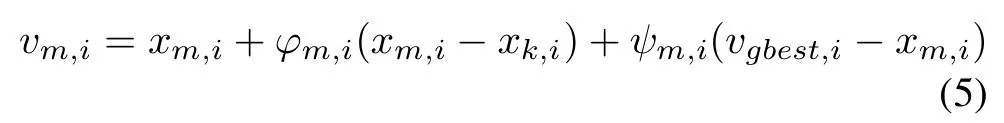
where m,k∈{1,2,...,SN}and k is a randomly chosen index and k/=m,and i∈{1,2,...,D}.ψm,iis a uniform random number in[0,1.5].vgbest,iis the ith element of the global best solution.This equation,which takes advantageof the informationfor global best solution to guide the search direction of new candidate solutions,improves the exploitation of ABC to some extent.

Based on the method in[13]and inspired by the Gaussian perturbation factor used for improving ant colony optimization(ACO)[22],we propose the heuristic Gaussian search strategy as follows,which is to make full use of the threesearchequationstobalancethecapabilityofexploitation and exploration:

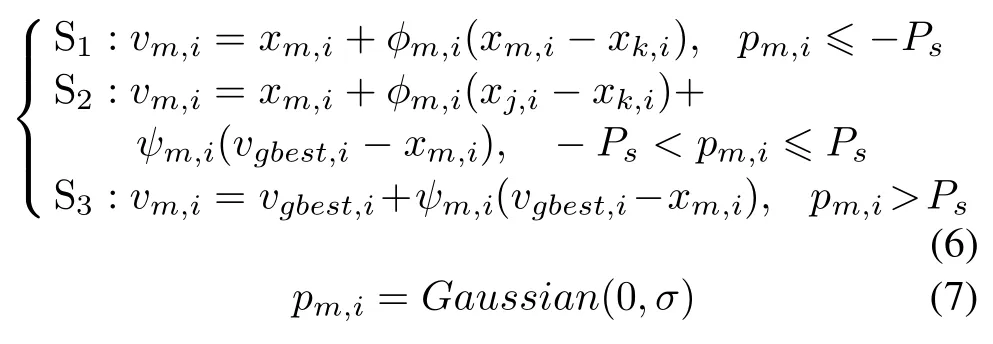
wherem,j andk are mutuallydifferentrandomintegerindices selected from{1,2,...,SN}and i∈{1,2,...,D}. pm,iis a random Gaussian factor from a Gaussian distribution where σ is a control parameter to balance the equations S2and S1,S3.S1is a standard ABC search equation which uses the random search method.This equation in the algorithm has a good performance for exploration. S2is a Gbest-guided equation which controls the search direction by(xj,i−xk,j)and(vgbest,i−xm,i).This equation improves the exploitation of ABC but at the cost of the exploring ability.S3is a global best guidance equation aiming at a local search around the best solutions.So,it has a better capability of exploitation.In this paper,we introduce a parameter Psto control the selection of the three different search equations so as to make full use of them.

Psis a constant.If σ takes a bigger value from(0,1), S1and S3will be chosen with a high probability.While σ takes a smaller value,S1will be chosen with a high probability.Depending on the experimental results,CSABC can achieve a better optimization performance when σ is 0.6.

Through the above search strategy,employed bees can choose three different search equations in probability, which can enhance the exploration performance as well as improvingthe exploitation of candidate solution search. Obviously,the search selection probabilityPsplays an important role in balancing the exploration and exploitation in the strategy.Note that when Psis equal to 0,S2in(6) does not work.When Pstakes 1,S2plays a major role in the strategy.As a result,the value of Psshould be selected in order to make full use of the proposed strategy and the experimentis used to investigate the inuence of this parameter Psin Section 4.The brief description for the search strategy of employed bee colony is shown in Algorithm 2.

Algorithm 2Heuristic Gaussian searching strategy

01:Set the search selection probability Ps

02:form=1 to SNdo

03: Produce the Gaussian factor pm,iusing(7)

04:ifpm,i≤−Psthen

05: vm,i=xm,i+φm,i(xm,i−xk,i)

06:if−Ps＜pm,i≤Psthen

10:end if

11:end if

12:end if

13: Apply a greedy selection process between Vmand Xm

14:ifsolution Xmdoes not improve,trialm= trialm+1

15:elsetrialm=0

16:end if

17:end for

3.3Gbest-guided neighborhood search strategy for onlooker bees

In the real world,an onlooker bee chooses a food source region,while the employed bee exploits the food source that she visited before,and tries to make a furtherexploitation tond a rich food source.In other words,the way of conducting the food source is different between employed bees and onlooker bees.The employed bees pay more attention to exploringmore food sources,while the onlooker bees focus on the exploitation of the food source that the employedbees foundbefore.However,employedbees and onlooker bees in the standard ABC algorithm have the same search equation to determine the new sources.Obviously,the search strategy contradicts the behavior of onlooker bees.Hence,Karaboga proposed a neighborhood search equation[16]as follows:

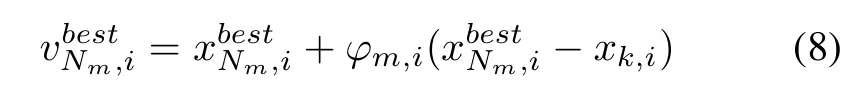
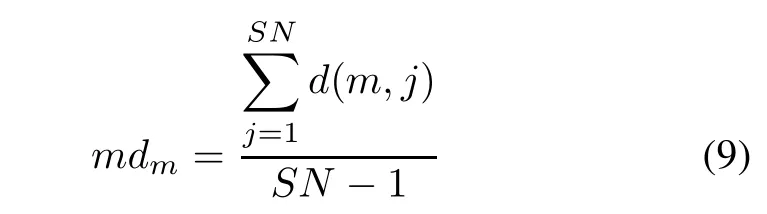
where d(m,j)is the Euclidean distance between Xmand Xj.Xjis the neighbor of Xmwhen d(m,j)is less than rmdm.r is the neighborhood radius and equal to 1 generally.IfthereareS solutionsin NmwhichincludesXm, the best food source in Nmcan be calculated as follows:

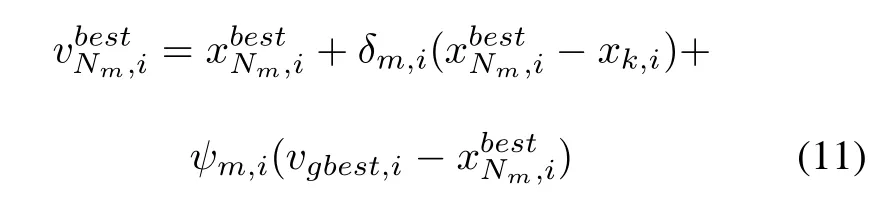
where δm,iis a random number from a Gaussian distribution N(0,1).ψm,iis a uniform random number in[0,1.5]. vgbest,iis the ith element of the global best solution.In (11),the current best solution is used to control the search direction so as to make a deep search around the bees’neighborhood.It not only enhances the local search accuracy,but also improves the convergence speed.The main procedure-codeis introduced in Algorithm 3.

Algorithm 3Gbest-guided neighborhood searching strategy

01:Set t=0 and i=1

02:Calculate the pmvalue by(4)

03:whilet＜SNdo

04:ifrandom＜pmthen

05: t=t+1

06: Calculate the mean distance by(9)

07: Determinetheneighborhoodsearchingfoodby (10)

09: Greedy selection is used betweenand

10:ifsolutiondoes not improve

11:thentriali=triali+1

12:elsetriali=0

13:end if

14:end if

15:i=i+1

16:end while

3.4Self-adaptiveperturbation strategyforbee colonyIt is the last and necessary strategy in the comprehensive mechanism of CSABC for improving the performance of ABC.It is used to prevent the algorithm from falling into the local optimum and enhance the diversity of population by Gaussian perturbation or random perturbation for the beecolonyat theendofeachiteration.Themainmethodof the strategy is to disturb the location of the current colony slightly.Firstly,calculate the average global optimal solution as follows:where m refers to the mth food source and SN is the food number.ObjValmis the best objective value of Xmin the ith cycle.Then,chose the appropriate strategy by comparing ObjValmwith ObjVali,mean.If the current optimal solutionis worse thanObjVali,mean,the followingoperation, i.e.Gaussian perturbation for the population in a larger area,will be applied to improve its search precision and exploitation.

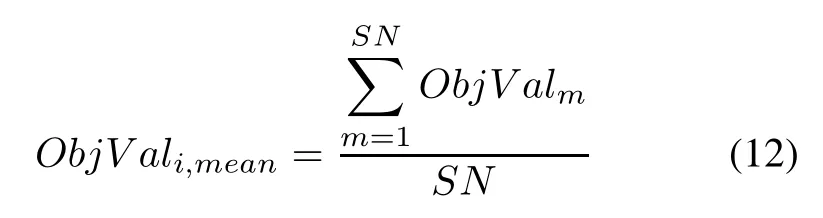
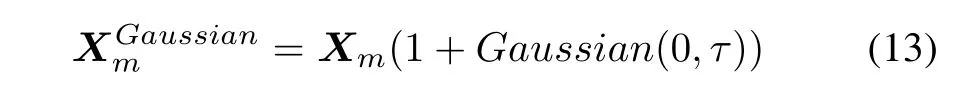
where Xmis the mth food source in the bee colony.Experimental results show that the improved algorithm can getbetteroptimizationperformancewhenτ takes0.5.Otherwise,the following random disturbance is to be used to disturb the location of Xmslightly in a smaller area.

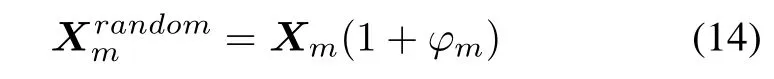
where ϕmis a randomnumber in[−1,1].The perturbation strategy for the bee colony is shown in Algorithm 4.

Algorithm 4Self-adaptive colony perturbation strategy

01:Calculate the ObjVali,meanby(12)

02:form=1 to SNdo

03:ifObjVali,mean＞ObjValmthen

04: Apply the Gaussian perturbation by(13)

05:else

06: Apply random perturbation by(14)

07:end if

08:end for

3.5Main steps of CSABC

Based on the aboveexplanationof improvedstrategies,the main steps of CSABC are given in Algorithm 5.

Algorithm 5The CSABC algorithm

01:Set the parameterSN,MaxCycle,Limit and ErrGoal

02:Perform Algorithm 1 to create the initial bee colony

04:whilethe halting criterion is not satiseddo

05:form=1 to SNdo

06: Generate a new food source Vmby Algorithm 2

07: Evaluate the food source Vm

08:end for

09: Perform Algorithm 3 for onlooker bees phase

10: Memorize the best food souse

11: Generate the scout bee by(1)

12: Apply self-adaptive perturbation strategy

13:end while

4.Experiments

In order to validate the performance of the CSABC algorithm on function optimization,27 benchmark functions described in Table 1[6,18]are used,where‘Min’is the minimum value of the functions and‘R’is the search range.f1−f7are continuous unimodal functions.f8is a discontinuous step function and f9is a noisy quartic function.f10−f15are low-dimensional functions which have onlyafew localminimums.f16−f27arehigh-dimensional multimodal functions.The numbers of local minimums for f16−f27increase exponentially with the dimensions [24].Theabovedifferentbenchmarkfunctions,whichhave good test performance,are difcult and complex unconstrained optimization problems.They can effectively validate the performance of CSABC in terms of convergence rate,global convergence accuracy and multimodal optimization.

Table 1 The 27 benchmark functions used in the experiments

Continued

In addition,in order to analyze the difference between the CSABC and other compared ABC algorithms,a popularstatistical methodnamelyWilcoxonsignedranks test [25]is usedintheexperiments.TheWilcoxonsignedranks test is a pairwise test that aims to detect signicant difference between two algorithms.The global best values of K independent runs are used as the samples for Wilcoxon signed ranks test.The signicance level of the test is set as 0.05.

In this section,we have carried out six different experiments and the usage of CSABC in the experiments is according to Section 3.5,namely main steps of CSABC. Meanwhile the parameters’settings of the experiments are stated at the beginning of each experiment in subsequent chapters.All the algorithms are implemented in Matlab and the experiments are done on an Intel Core i5-23102.9 and 2.89 GHz machine with 3.34 GB RAM under the WIN-XP platform.

4.1Parameters analysis of CSABC algorithm

4.1.1 Impact of selection probability Pson the performance of CSABC

According to the explanation of the selective probability Psin the employed bees process of CSABC,we note that it plays an important role for the performance of CSABC. In order to select a suitable Psof the CSABC for a better balance between exploitation and exploration,ve different kinds of 30 dimensional benchmark functions are used to investigate the inuence of the parameter.The functions are Sphere(f1),Rosenbrock(f18),Rastrigin(f20), Griewank(f22)and Ackley(f24)[13].We set the population size SN=80,limit=500,maximum number of function evaluations MaxCycle=5 000,objective search accuracy ErrGoal=e-50(values of function error less than 1e-50 are reported as 0).

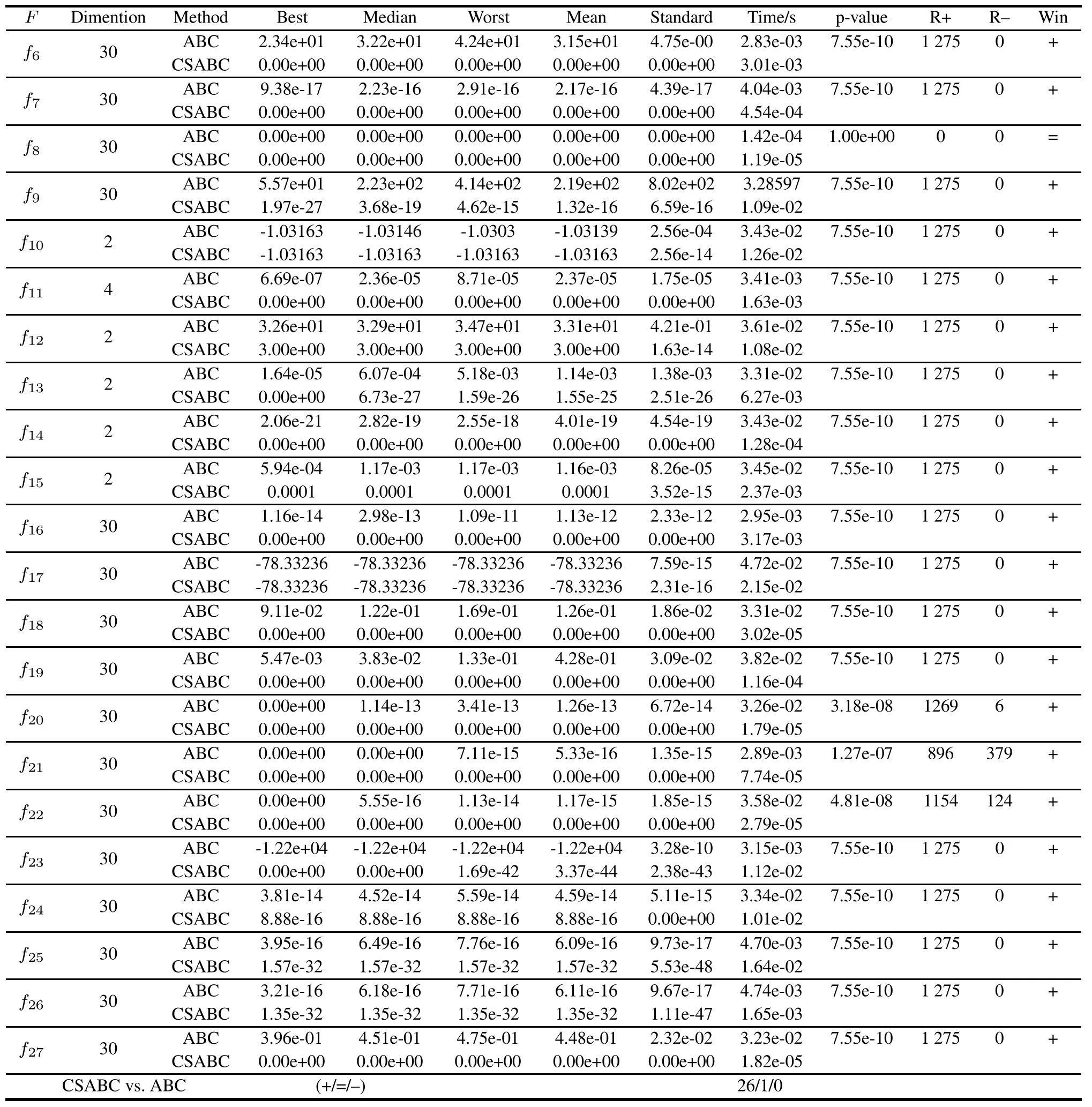
The results of mean and standard deviation values are summarized in Table 2 through 30 independent runs of each function.From Table 2,wend that Pscan inuence the results.When Psis around 0.5,CSABC has a faster convergencespeed and better results on Rosenbrock and Ackley functions.For the other three functions,it can achieve the optimal solution whatever Psis.In order to illustrate the inuence of Psfor the algorithm more evidently,convergence curves of CSABC for the rest three functions are shown in Fig.1.It can be observed that CSABC has less generation to reach the better results and faster convergence speed when Psis 0.5 in the evaluation process of the three functions.As a result,Psis set to 0.5 for all other experiments so as to get the best performance for CSABC.

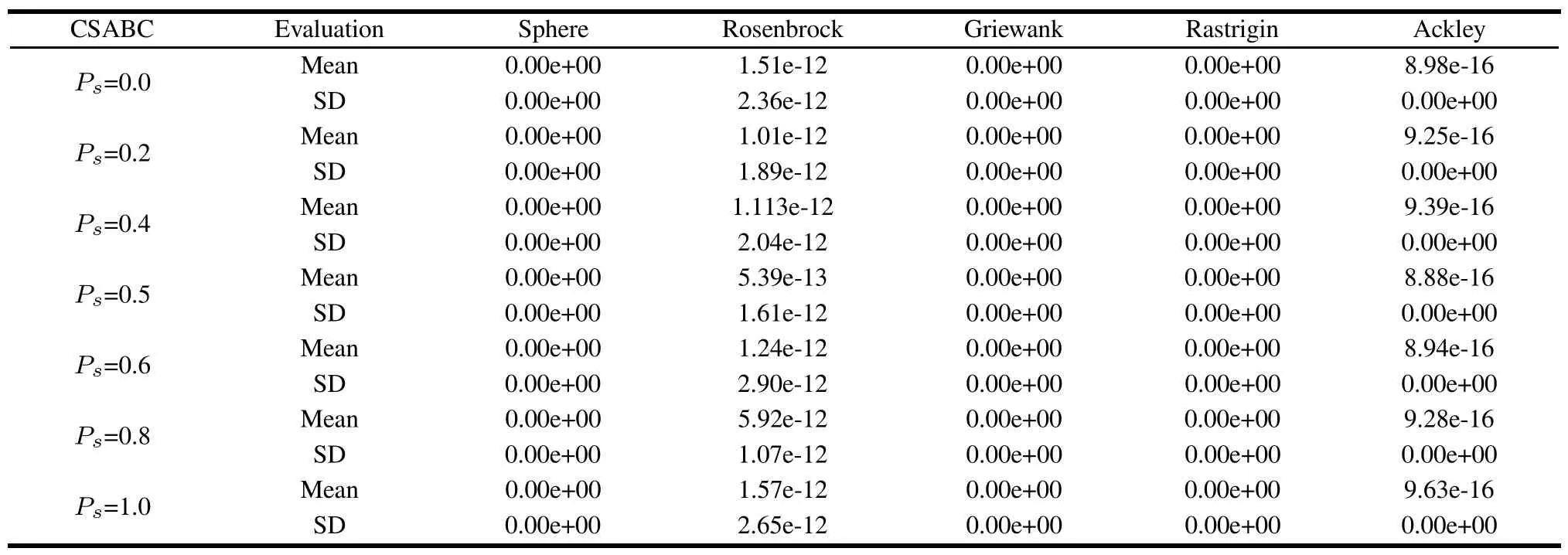
Table 2 Infuence of different values of Pson the performance of CSABC

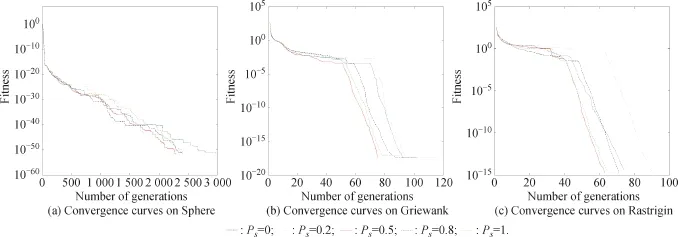
Fig.1 Convergence curves of CSABC with different Pson functions Sphere,Griewank,and Rastrigin

In this experiment,we discuss the inuence of different population sizes SN on the performance of CSABC.The results are summarized in Table 3 in terms of the best, worst,mean,standard deviation of the solutions and mean time of the solutions for each test functions obtained inthe 50 independent runs.We set limit=100,MaxCycle= 500,ErrGoal=1e-50,Ps=0.5 and D=30.The convergence curves of CSABC with different population sizes are presented in Fig.2.As can be seen from Table 3,the convergence speed,stability and robustness of the CSABC algorithm are all increasing along with the increase of the population size,but the time consumption also dramatically increases.In Fig.2,we cannd that the convergence curves of the algorithm are similar when SN is larger than 100.For the algorism’s performance and operation efciency concern,we set SN=100 so as to get more ideal optimization performance.

Fig.2 Convergence curves of CSABC with different SNs on functions f9,f19and f27

Table 3 Infuence of different numbers of population on the performance of CSABC with f9,f19and f27

4.2Comparison with standard ABC algorithm

In

this experiment,the performance of CSABC is comparedwith that of ABC.We set SN=100,MaxCycle=5000, ErrGoal=1e-50,limit=100 and Ps=0.5.

The statistical and Wilxcon singed ranks test results are summarized in Table 4 obtained by 50 independent runs. In addition,if p-value in Table 4 is less than 0.05(5%signicance level),it is a strong evidence against the null hypothesis,indicating that the compared two algorithms are statisticallydifferentandhavenotoccurredbychance[25].‘R+’represents the sum ranks for the problems in which CSABC outperform the compared algorithm while‘R–’indicates the sum of ranks for the opposite.‘Win’represents the winner algorithm in the pairwise comparison.‘+’indicates the winner algorithm is CSABC,‘–’represents the winner algorithm is the compared algorithm and‘=’illustrates that there has no signicant difference between the two algorithms.

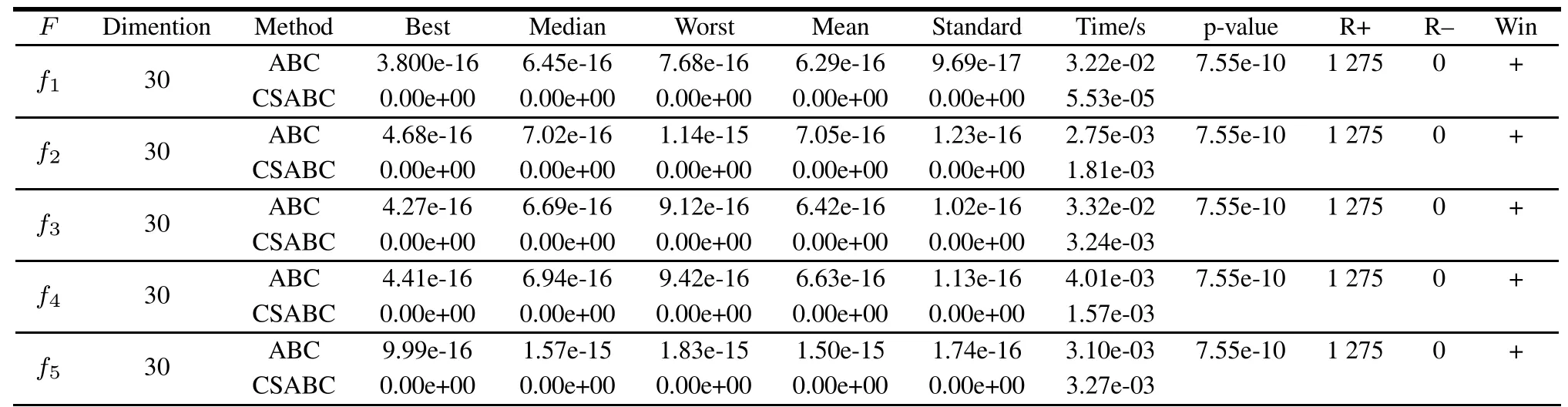
Table 4 Comparison between ABC and CSABC based on 27 test benchmark functions(α=0.05)

Continued

The statistical results from Table 4 suggest that the convergence precision and speed of CSABC are better than ABC.Particularly,CSABC can nearlynd the global optimal solutions on all functions expected for f24,f25and f26,while the results in terms of the best,median,worst, mean,and standard of CSABC are obviously better than those of ABC on the three test functions.Meanwhile,the mean runningtime of CSABC is less than that of ABC.On the other hand,when the(+/=/–)values are examined from Table4,itcanbesaidthatCSABC isstatistically moresuccessful than ABC in solving the 27 benchmark functions.

Furthermore,in order to illustrate the different performances of ABC and CSABC,four representative graphs presenting the comparison on convergence characteristics of the evolutionary process are shown in Fig.3.It can be seen that the convergence speed of CSABC is faster than that of ABC as Fig.3 indicates.In short,the superiority in terms of search accuracy and efciency of CSABC should be attributed to a better balance between exploitation and exploration.

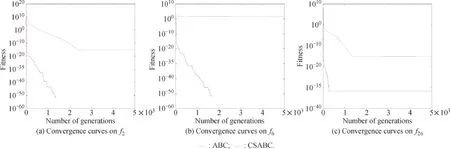
Fig.3 Convergence curves of CSABC and ABC on the four test functions with D=30

4.3Comparison with ABC-based algorithms

In order to further illustrate the superiority of CSABC, the performanceof CSABC is compared with GABC[13], qABC[16]andMABC[18].Thevetestfunctionswith30 and 60 dimensions respectively are selected from Table 1 as[13]indicated.And the statistical results are summarized in Table 5 and Fig.4.All the parameter settings are the same as those of GABC in[13],i.e.SN=80,Max-Cycle=5 000,ErrGoal=1e-20 and 30 runs.It can be seen from Table 5 that the standard statistical results including best,median,worst,mean and standard of CSABC show obvious superiority compared with qABC,GABC and MABC,especially for the optimization of functions Sphere,Griewank and Schaffer.Meanwhile,the mean running time of CSABC is less than the compared algorithms except the Rosenbrock function.When the(+/=/–)values for Table 5 are examined,it can be conrmed that CSABC has provided statistically better solutions than the compared algorithms.As can be seen from Fig.4,CSABC has a signicantly faster convergence speed than the other three ABCs algorithms.In a word,CSABC works better in all cases and has a superior optimization ability than qABC,GABC and MABC from Table 5 and Fig.4 on the basis of above parameters settings.

Table 5 Comparison with qABC,GABC,MABC and CSABC on fve test functions(α=0.05 and NA indicates CSABC vs.CSABC)

Continued

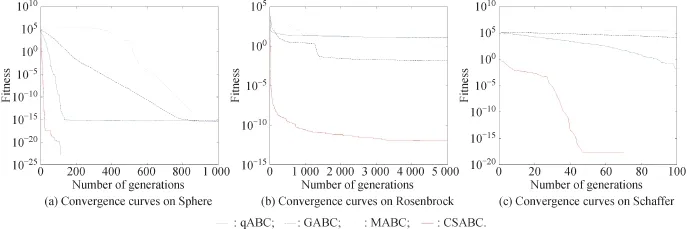
Fig.4 Convergence curves of different ABC-based algorithms on the three test functions

4.4Comparison for high dimensional functions

In this experiment,we compare the optimization quality of the CSABC with qABC,GABC and MABC in different high dimensions with low population sizes.We set the SN=50 and other parameter settings are invariant as described in Section 4.3.The mean results of 30 independent runs and Wilxcon singed ranks test are summarized in Table6(NAindicatesCSABC vs.CSABC).Furthermore,we present two representative cases of the convergencecurves for MABC and CSABC with 2 000 dimension benchmark functions for function f3and f19,which are shown in Fig.5.

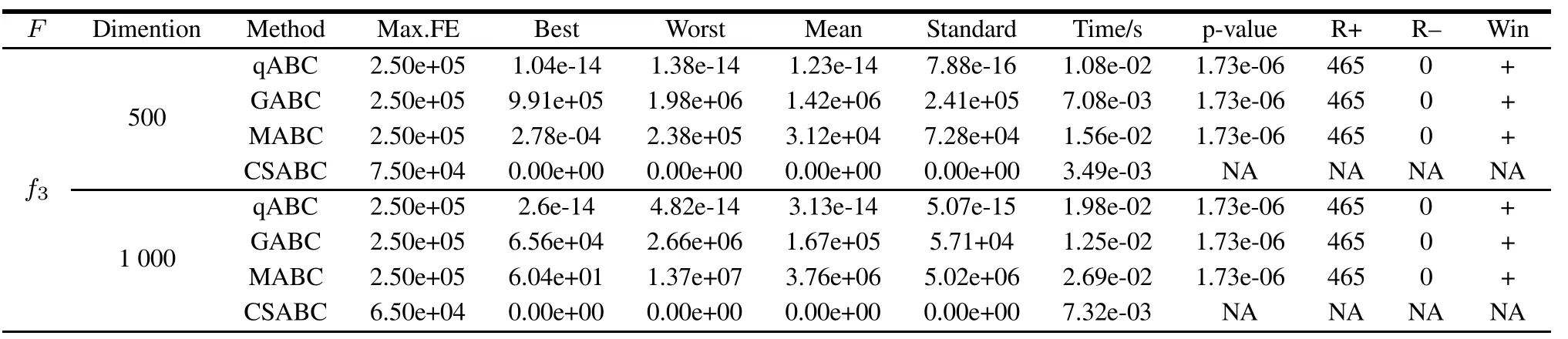
Table 6 Comparison between different ABC algorithms on f3,f17and f19with high dimensions(α=0.05)

Continued

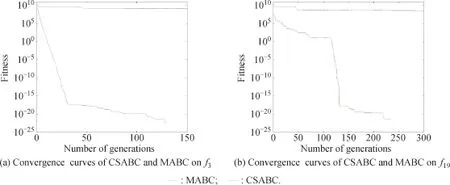
Fig.5 Convergence curves of MABC and CSABC for benchmark functions with 2 000 dimensions on f3and f19

As seen from Table 6,the advantages in terms of best, median,worst,mean,standard and mean time of CSABC are very outstanding among the four ABCs.Especially for f3,f17and f19with 2 000 dimensions,the mean of CSABC gets the theoretical optimal value.Meanwhile, CSABC can solve the three problems of different high dimensions in all 30 runs while the other three improved ABC algorithms cannot.Moreover,CSABC requires less mean Max.FE than the other three ABC-based algorithms in f3and f19.When examining the value of(+/=/–)from Table 6,it can be illustrated that the CSABS has statistically better solutions that the compared ABC-based algorithms.In Fig.5,it can be observed that CSABC has a better performance on the convergence speed within less generationthan MABC.In a word,the results fromTable 6 and Fig.5 illustrate that the CSABC algorithm is superiorto other three kinds of improved ABC in the aspects of convergence accuracy,speed and stability for optimizing the high dimensional functions.

4.5Comparison for the multimodal functions

In order to analyze the optimization performance for multimode functions,CSABC is compared with qABC and MABC basedon the fourmultimodalfunctions.Thestatistical results and Wilxcon singed ranks test are summarized in Table 7,where ratio refers to the percentage of searching all the global optimal solutions for the functions.In the experiment,we set the parameters as those in Section 4.2.

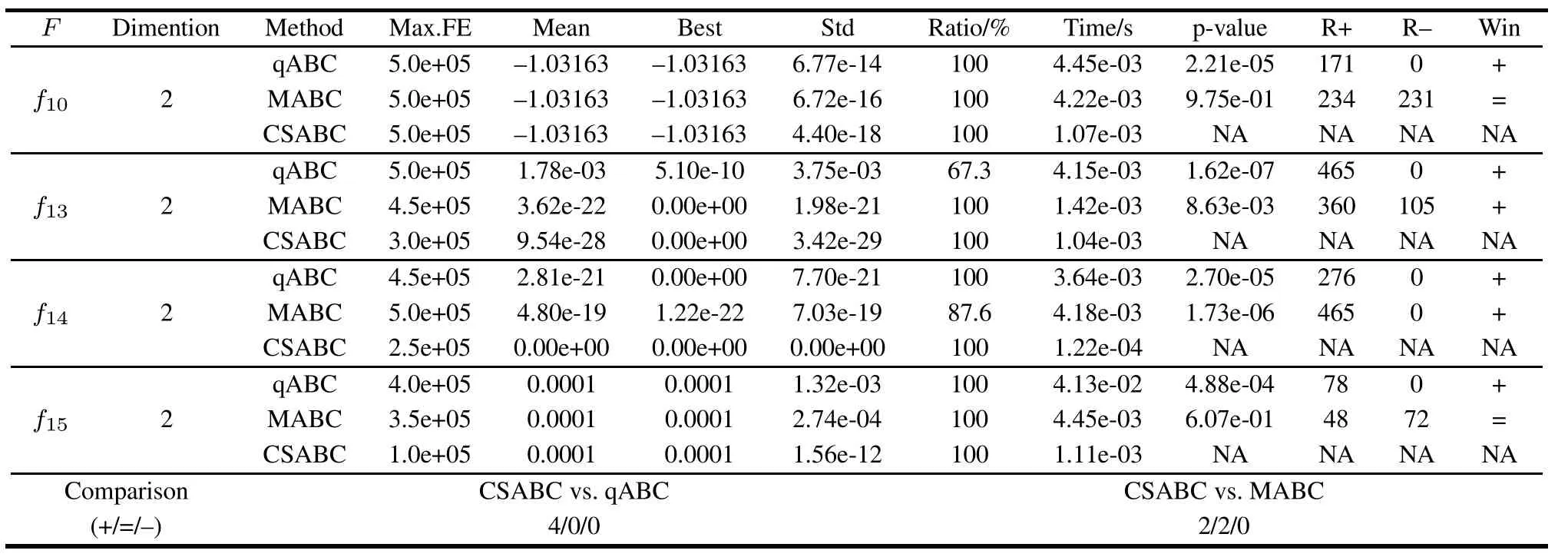
Table 7 Comparison with qABC,MABC and CSABC for multimodal functions(α=0.05)

From Table 7,we see that the CSABC can get all the theoretical optimal values for the multimodal functions with low time consumption compared with other two algorithms.Moreover,CSABC gives smaller standard deviations of function values.It means that the solution quality of CSABC is more stable than qABC and MABC.In addition,in the three functions,CSABC requires less mean Max.FE.When the values of(+/=/–)are examined,it can be indicated that the CSABC is statistically better than the compared algorithms for optimization of the four multimodal functions.

4.6Analysis of the population diversity

The populationdiversityis directly related to the optimization performance of ABCs[26]and it can be calculated as follows:

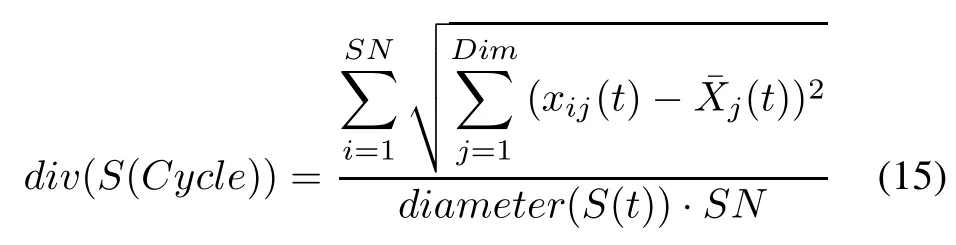
where diameter(S(t))is the diameter of the bee colony, namely the Euclidean distance between the most remote individuals,¯xj(t)is the mean jth location of X and t is the current cycle number.

Inthis experiment,weset theErrGoal=1e-100andother parameters settings are the same as those in Section 4.2. The mean diversity curves of CSABC and MABC with 30 independent runs for f1and f24are shown in Fig.6.

Fig.6 Comparison on the diversity performance

It can be observed that the MABC algorithm keeps better population diversity at the beginning of the evolution, but it turns weak with the increasing number of generation.However,the CSABC algorithm keeps a better performance in the process of evolution,thus it is able tond the global optimal value at a large probability.

5.Conclusions

In this paper,we propose an efcient optimization algorithm named CSABC through explaining the heuristic Gaussian search strategy for employed bees,the global best-guided neighborhood search equation of onlooker bees,and the self-adaptive perturbation method for bee colony and introducing the chaos opposition-based learning method for population initialization.By these means, CSABC achieves a better balance between explorationand exploitation.The experimental results and Wilxcon signed ranks test based on 27 benchmark functions show that the performanceof the CSABC algorithmis superior to that of ABC,qABC,GABC andMABCalgorithms,especiallyfor the high-dimensional complex functions and multimode optimization problems.

[1]D.Karaboga.An idea based on honey bee swarm for numerical optimization.Kayseri:Erciyes University,2005.

[2]J.Kennedy,R.Eberhart.Particle swarm optimization.Proc.of the IEEE International Conference on Neural Networks,1995: 1942–1949.

[3]K.S.Tang,K.F.Man,S.Kwong,et al.Genetic algorithms and their applications.IEEE Signal Processing Magazine,1996, 13(6):22–37.

[4]M.Dorigo,T.Stutzle.Ant colony optimization.Cambrige: MA MIT,2004.

[5]D.Karaboga,B.Basturk.A powerful and efcient algorithm for numerical function optimization:articial bee colony (ABC)algorithm.Journal of Global Optimization,2007, 39(3):459–471.

[7]D.Karaboga,C.Ozturk.Anovel clustering approach:articial bee colony(ABC)algorithm.Applied Soft Computing,2011, 11(1):652–657.

[8]K.Chandrasekaran,S.P.Simon.Multi-objective unit commitment problem with reliability function using fuzzied binary real coded articial bee colony algorithm.IET Generation, Transmission&Distribution,2012,6(10):1060–1073.

[10]Y.M.Huang,J.C.Lin.A new bee colony optimization algorithm with idle-time-basedltering scheme for open shopscheduling problems.Expert Systems with Applications,2011, 38(5):5438–5447.

[11]T.J.Hsieh,H.F.Hsiao.Forecasting stock markets using wavelet transforms and recurrent neural networks:an integrated system based on articial bee colony algorithm.Applied Soft Computing,2010,11(2):2510–2525.

[12]D.Karaboga,B.Akay.A comparative study of articial bee colony algorithm.Applied Mathematics and Computation, 2009,214(1):108–132.

[13]G.P.Zhu,S.Kwong.Gbest-guided articial bee colony algorithm for numerical function optimization.Applied Mathematics and Computation,2010,217(7):3166–3173.

[14]J.F.Schutte,A.A.Groenwold.Sizing design of truss structures using particle swarms.Structural and Multidisciplinary Optimization,2003,25(4):261–269.

[15]F.Kang,J.J.Li,Z.Y.Ma.Rosenbrock articial bee colony algorithm for accurate global optimization of numerical functions.Information Sciences,2011,181(6):3508–3531.

[16]D.Karaboga,B.Gorkemli.A quick articial bee colony (qABC)algorithm and its performance on optimization problems.Applied Soft Computing,2014,23:227–238.

[17]R.Storn,K.Price.Differential evolution-a simple and efcient heuristic for global optimization over continuous spaces.Journal of Global Optimization,1997,11(4):341–359.

[19]D.Gehlhaar,D.Fogel.Tuning evolutionary programming for conformationallyexible molecular docking.Proc.of the FifthAnnual Conference on Evolutionary Programming,1996: 419–429.

[20]B.Liu,L.Wang,Y.H.Jin,et al.Improved particle swarm optimization combined with chaos.Chaos,Solutions&Fractals, 2005,25(5):1261–1271.

[21]Z.H.Zhan,J.Zhang,Y.Li,et al.Adaptive particle swarm optimization.IEEE Trans.on Systems,Man,and Cybernetics-Part B:Cybernetics,2009,39(6):1362–1381.

[22]P.Korosec,J.Silc.The differential ant-stigmergy algorithm applied to dynamic optimization problems.Proc.of the IEEE Congress on Evolutionary Computation,2009:407–410.

[23]W.Y.Gong,Z.H.Cai,L.X.Jiang.Enhancing theperformance of differential evolution using orthogonal design method.Applied Mathematics and Computation,2008,206(1):56–69.

[24]Y.W.Leung,Y.Wang.An orthogonal genetic algorithm with quantization for global numerical optimization.IEEE Trans. on Evolutionary Computation,2001,5(1):41–53.

[25]J.Derrac,S.Garcia,D.Molina,et al.A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evolution Computation,2011(1):3–18.

[26]J.Riget,J.S.Vesterstrom.A diversity-guided particle swarm optimizer-the ARPSO.Aarhus:Unversity of Aarhus,2002.

Biographies

Mudong Li was born in 1987.He received his M.S.degree in circuits and system from Air Force Engineering University in 2010.He is now studying in Air Force Engineering University to pursue his Ph.Ddegree ofweapon science andtechnology. His research interests are articial intelligence optimization algorithms and optimal control.

E-mail:modern lee@163.com

Hui Zhao was born in 1973.He received his Ph.D. degree in weapon science and technology from Air Force Engineering University,in 2011.He is currently a professor in Department of Aeronautics and Astronautics Engineering,Air Force Engineering University.He has been engaged in teaching and researching on weapon systems and application engineering and optimal control.

E-mail:zhaohui kgy@163.com

Xingwei Weng was born in 1978.He received his Ph.D.degree in weapon science and technology from Air Force Engineering University in 2009.He is currently an instructor and working in Department of Aeronautics and Astronautics Engineering,Air Force Engineering University.His research interests are weapon systems and application engineering and optimal control.

E-mail:weng kgy@163.com

Hanqiao Huang was born in 1982.He received his Ph.D.degree in Navigation,guidance and control from Northwestern Polytechnical University in 2010.He is currently an instructor and working in Department of Aeronautics and Astronautics Engineering,Air Force Engineering University.His research interests are optimal control and control science and engineering.

E-mail:cnxahhq@126.com

10.1109/JSEE.2015.00068

Manuscript received May 23,2014.

*Corresponding author.

This work is supported by the Aviation Science Foundation of China(20105196016)and the Postdoctoral Science Foundation of China (2012M521807).