Signal difference-based deadband H∞control approach for networked control systems with limited resources

Yingying Liu,Weiwei Cheand Yunkai Chu

1.School of Information Engineering,Shenyang University,Shenyang 110044,China;

2.Key Laboratory of Manufacturing Industrial Integrated Automation,Shenyang University,Shenyang 110044,China;

3.Shenyang Institute of Automation Chinese Academy of Sciences,Shenyang 110016,China

Signal difference-based deadband H∞control approach for networked control systems with limited resources

Yingying Liu1,*,Weiwei Che2and Yunkai Chu3

1.School of Information Engineering,Shenyang University,Shenyang 110044,China;

2.Key Laboratory of Manufacturing Industrial Integrated Automation,Shenyang University,Shenyang 110044,China;

3.Shenyang Institute of Automation Chinese Academy of Sciences,Shenyang 110016,China

This paper investigates a signal difference-based deadband H∞control approach for networked control systems(NCSs) with limited resources.The effects of variable network-induced delays,sampling intervals and data transmitting deadbands are considered simultaneously and the model of the NCS is presented. A Lyapunov functional is adopted,which makes full use of the network characteristic information including the bounds of network delay(BND),the bounds of sampling interval(BSI)and the bounds of transmission deadband(BTD).In the meanwhile,the new H∞performance analysis and controller design conditions for the NCSs are proposed,which describe the relationship of BND, BSI,BTD and the system’s performance.Three examples are used to illustrate the advantages of the proposed methods.The results have shown that the proposed method not only effectively reduces the data trafc,but also guarantees the system asymptotically stable and achieves the prescribed H∞disturbance attenuation level.

networked control system(NCS),H∞control,variable network-induced delay,variable sampling interval,transmission deadband.

1.Introduction

Networked control systems(NCSs)are such control systems where the control loop is closed via communication networks[1].NCSs have great advantages,for example,low cost,reduced weight and power requirements, simple installation and maintenance,and high reliability [2,3].However,NCSs also introducemany new challenges in control system design such as time-varying networkinduced delays,limited network resources or data packet congestion,and these disadvantages might be main resources for inuencing the stability and the performance degradation of the NCSs[4–7].Recently,some works have discussed the control problem of NCSs with delays and dropout packets[8–12].However,the effect of sampling intervals has not been investigated in the aforementioned papers.In NCSs,the limitation of the network resources is primarily caused by the limited bandwidth of the communication network,then the limited bandwidth of the network produces a situation,where a smaller samplingperiodmaynot result in a better system performance. A small sampling period will produce too many sensing data in the network channel,and this will bring about the overloading and congestion of the network,and result in more data packet dropouts and longer delays,and thus degrade the system performance[1,13].Presently,Wang and Yang proposed the H∞controller design approach for the NCSs by using an active-varyingsampling period method. Cloostermal et al.[15]presented a discrete-time model for the NCSs that incorporates all network phenomena: time-varyingsamplingintervals,packetdropoutsandtimevarying delays,and gave stabilizing controller design.To the best of the author’s knowledge,the control problem of NCSs with time-varying sampling has not been fully investigated and still remains challenging.

On the other hand,a large amount of data packets transmitin thelimitednetworkbandwidth,so,theprobabilityof congestion increases,which may lead to higher transmission delay and packet loss[16].Therefore,some scheduling methods have been proposed in the past years such as try-once-discard(TOD)protocol and round-robin(RR) protocol.Both protocols allow only one output to be transmitted via the channel at a time.Walsh et al.[17]used the TOD protocol to deal with the packets scheduling and obtained the maximum allowable transfer interval.Xu et al. [18]applied a conventionalRR scheduling to deal with thecommunication constraints for NCSs,wherein the packets were transmitted in axed order.Liu et al.[19]investigated the exponential stability and the induced L2-gain of NCSs that were subject to time-varying transmission intervals,time-varying transmission delays and communication constraints,wherein the scheduling of sensor information towards the controller is ruled by the classical RR protocol.However,in the works mentioned above,it can be found that the total data information over the network channelhas not been reducedat each samplinginstant,and the inuences of the amount of data transmission on system performance were not considered.Transmission data losses and communication delays strongly affect the stability and performanceof the closed-loop systems.The most effective way to improve system performance is to reduce network transmission[20].In[21]and[22],the transmission data in networked control systems were reduced by applying deadband control.In these communication networks,the data packets were sent over only if the signal value changed more than a given threshold.These results have showed that the deadbandcontrol could reduce effectively the amount of the transmission data.Recently,Zhao et al.[23]proposed a packet-based deadband control approachforinternet-basedNCSs,buttheproposedapproach only reduced the transmission of control input signals,and it did not consider the inuences of the transmission of state signals in NCSs.However,for the NCSs with variable network-induced delays,variable sampling intervals and signal transmission deadbands,fewer results are available to study the consequences of all these phenomena in a common framework.It is therefore necessary to conduct an analysis on the network-induced delay,sampling interval and transmission deadband,and study how much these effects work on the overall performance of NCS.

In contrast with the above previous works,this paper explores a signal difference-based deadband H∞control approach to decrease the data transmission in the NCSs.By using the input delay approach,the effects of network-induced delays,sampling intervals and transmission deadbands are included in the NCS model.By employing a Lyapunov functional which takes full advantages of the information of network-induced delays,sampling intervals and transmission deadbands,the condition of H∞controller design is given.The obtained condition is dependent on the bounds of sampling interval(BSI),the bounds of network delay(BND)and the bounds of transmission deadband(BTD).Finally,numerical examples are provided to validate the proposed control strategy.

2.Problem formulation

The NCSs with two transmission deadbands can be described as in Fig.1.

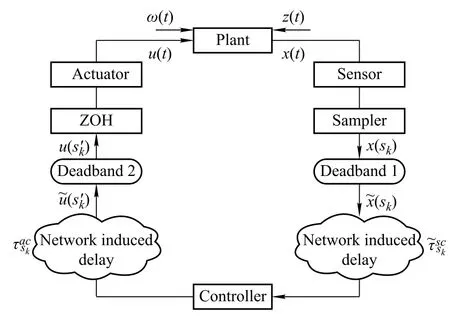
Fig.1 Structure of the NCS with two transmission deadbands

In the NCSs,transmission deadband 1 is set up in the side of the sensor to controller and transmission deadband 2 is set up in the one of the controller to the actuaor.The plant is a continuous-timesystem whose state-space representation is given by

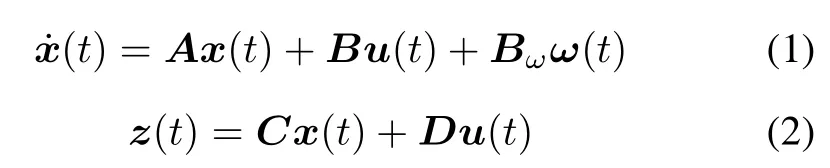
where x(t)∈Rnis the system state,ω(t)∈Rmis the disturbance,u(t)∈Rpisthecontrolinput,andz(t)∈Rqis the controlled output.A,B,Bω,C,D are some constant matrices of appropriate dimensions.

In this paper,both the state and the control input signals are processed by transmission deadbands before they are sent to the controller and the actuator respectively.At the sametime,it is assumedthat thesensorandthe samplerare clock-driven,while the controller,the zero-order holder, and the actuator are event-driven.The implementation of deadbandcontrolwillleadtonetworkdatatransmissionreductionwhilemaintainingacceptablesystemperformance. In Fig.1,we denote the input signal of transmission deadband 1 as x and its output signal as˜x.At the same time, the input signal and the outputsignal of transmissiondeadband2 are˜u and u,respectively.The samplinginstants are denoted as sk(k=0,1,...,∞).A node with the transmission deadband compares the previous value˜x(sk)to the most recent value x(sk+1).The data packets are sent over the communication network only,if the signal value changes more than a given threshold.Thus,transmission deadband 1 can be described as

where i=1,2,...,n,and δ1i|xi(sk+1)|is the threshold of the deadband.δ1iis the weighting of the deadband threshold.

Remark 1If the absolute value of the difference between xi(sk+1)and˜xi(sk)is within the threshold of the deadband,then no update data are sent to the network.It can be seen that δ1iinects the size of the deadband,and as δ1iincreases,the node broadcasts fewer messages.

Implementing deadbands to reduce network trafc produces uncertainty in the state of the NCSs(1)and (2).Dene Δ1(sk+1)= diag{Δ11(sk+1),Δ12(sk+1), ...,Δ1n(sk+1)},Δ1i(sk+1)∈[−δ1i,δ1i],then(3)can be included in the following equality:

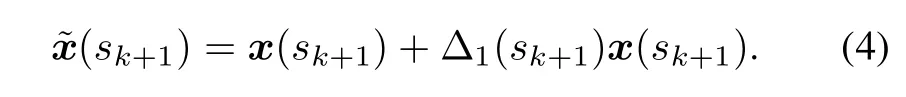
The sampling interval Tk=sk+1−skis time-varying and its lower bound and upper bound are known:

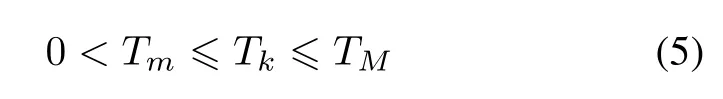
where Tmand TMdenote the lower boundof the sampling interval and the upper bound of the sampling interval,respectively.

In this paper,we consider the case of sk+τk＜sk+1, thatis,thenetworkdelayisless thanonesamplinginterval. Then at the instant sk,we have

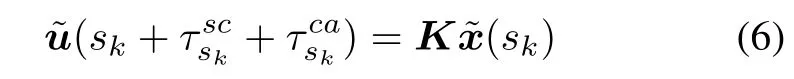
where K is the state-feedback gain to be determined later. For convenience,denote sk′=sk+τscsk+τcask.

In the following,the relation between the input signal˜u and the output signal u in the transmission deadband2 can be described as

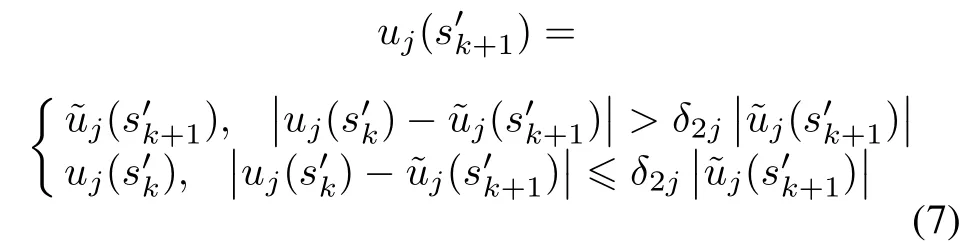
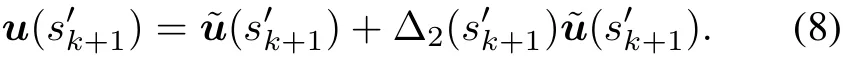
Combining(4)and(8),the controlinputsignalcanbewritten as

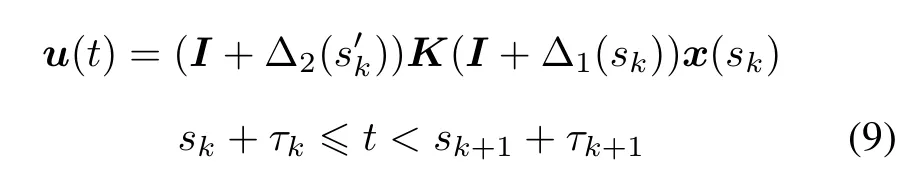
where I denotes the identity matrix of appropriate dimensions.|Δ1i(sk)|≤δ1iand|Δ2j(s′k)|≤δ2j.For the sake of simplicity,it is assumed that δ1i=δ1and δ2j= δ2. Then,it is not difcult to get Δ1i(sk)∈[−δ1,δ1]and Δ2j(s′k)∈[−δ2,δ2].In the following,for the sake of simplicity,we denote Δ1(sk)and Δ2(s′k)as Δ1and Δ2,respectively,and we call δ1and δ2as the BTD.It is clear that in the same network conditions,with the value of BTD increasing,fewer data are sent in the network channel.

Modeling of continuous-time systems with discretetime control inputs was investigated in[24].The digital control law may be represented as follows by using the input delay approach:

Denote d(t)=t−sk,the piecewise-constant control law(10)can berepresentedas acontinuous-timecontroller with a time-varying piecewise continuous delay:

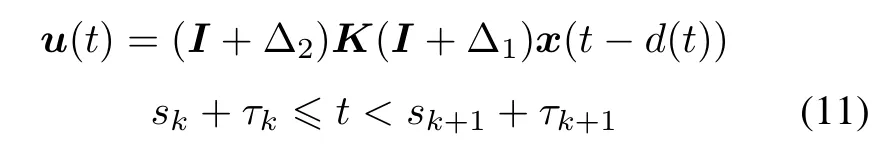
where d(t)=t−skis piecewise linear with the derivative ˙d(t)=1 for t/=sk+τk.

At the same time,we have

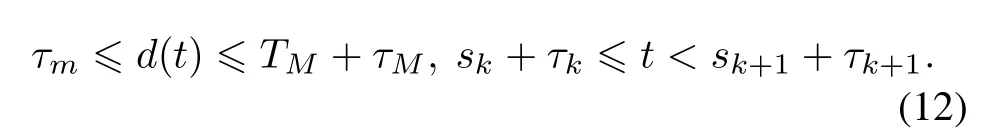
Since thenetworkcommunicationdelayis smaller thanthe sampling interval,we obtain τm≤τM≤Tm≤TM.Let τM/Tm≤ρ≤1,then we can write(12)as

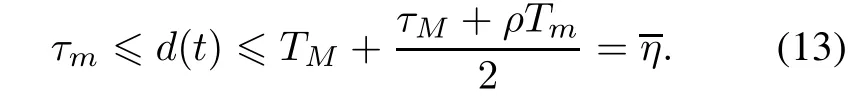
We call η the maximum allowable equivalent delay bound (MAEDB)[11].It is clear that in the same network conditions,the larger the value of MAEDB is,the larger the allowable networked communication delays and sampling intervals are in NCSs.

Substituting the controller(11)into NCSs(1)and(2), we can obtain the closed-loop networked control system:

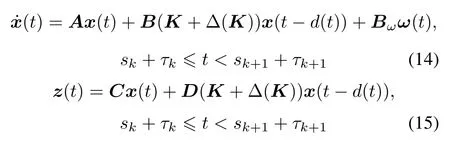
for x(0)=0 and all ω(t)/=0.The scalar γ is a prescribed positive scalar and indicates an H∞disturbance attenuation level.

Remark 2By the input delay approach,we give a general framework for the linear matrix inequality(LMI) approachto derivethe H∞performanceanalysis condition for the NCSs with networkdelays,variablesampling intervals and signal transmission deadbands.It should be noted that the delay d(t)is piecewise linear with˙d(t)=1 for t/=sk+δk,and it integrates the information of network communication delays and sampling intervals.

3.Main results

3.1RobustH∞performance analysis for the NCSs with transmission deadbands

Given the bounds of network delays τmand τM,the bounds of sampling intervals Tmand TM,and transmission deadband bounds δ1and δ2,assuming that the matrices A,B,C,D,Bωand the control gain K in systems(14)and(15)are known,we will formulate the conditionsunderwhichtheclosed-loopnetworkedcontrolsystem with signal transmission deadbands is robustly stable with an H∞disturbance attenuation level γ.

Theorem 1Consider the NCS in Fig.1.For given scalars τm,τM,Tm,TM(0≤τm≤τM≤Tm≤TM), δ1＞0,δ2＞0,0≤α＜1,τM/Tm≤ρ≤1,andamatrix K,the closed-loop NCSs(14)and(15)are asymptotically stable with an H∞disturbance attenuation level γ if there exist matrices P=PT＞0,Qi=QiT＞0(i=1,2,3), Uj=UjT＞0(j=1,2),and Nl,Tl,Ml,El(l=1,2, 3,4,5)of appropriate deimensions,such that

ProofConsider the following piecewise Lyapunov functional:

where

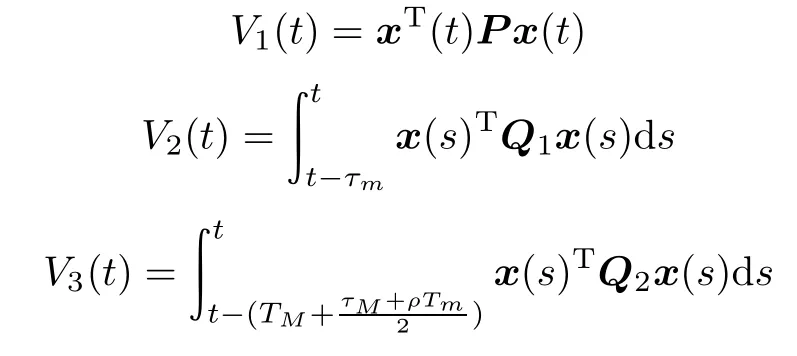
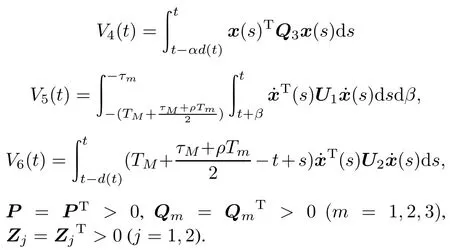
Obviously,V(t)is discontinuous.NotethatV(t)is continuous and positiveexcept the instantssk+δk.Therefore, we consider the following two cases:

(i)For sk+τk＜ t＜ sk+1+τk+1,calculating the derivative of V(t)with respect to t along the solutions of the system and using the Leibniz-Newton formula,yield that

where

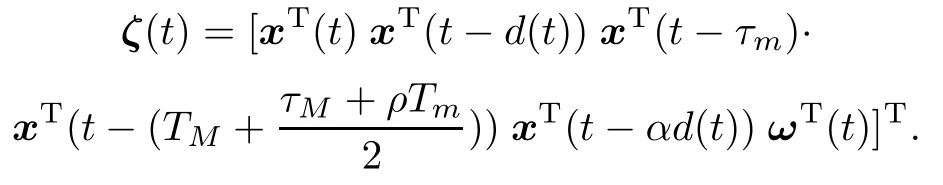
By the Schur complements,combining(17)to obtain ˙V(t)+zT(t)z(t)−γ2ωT(t)ω(t)＜0 for tk＜t＜tk+1(In the following,we denote tk=sk+τkfor k= 0,1,2,3,...).On the other hand,it is clear that˙V(t)＜0 when ω(t)=0.This implies that system(14)with ω=0 is asymptotically stable for tk＜t＜tk+1.

(ii)It is noted that d(t)is discontinuous at the instants sk+τk.There exist:for t=sk+τk,d(t)=τk,∀k∈N; for t=(sk+τk)−,d(t)=sk+τk−sk−1,∀k∈N.

Note that the value of the state x(t)before and after the instants sk+τkremains unchanged(since x(t)is continuous).Then,we have Vi((sk+τk)−)=Vi(sk+τk)(i= 1,2,3,5)inLyapunovfunctional(19).Moreover,forV4(t) and V6(t),there exist V4((sk+τk)−)≥ V4(tk)and V6((sk+τk)−)≥V6(sk+τk).Thus,V((sk+τk)−)≥V(sk+τk)for k=0,1,2,3,....For t∈[tk,tk+1),we have follows that

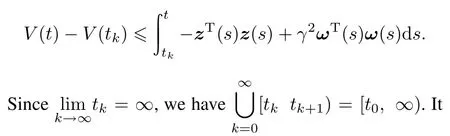
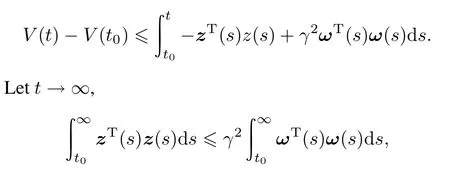
which means‖z(t)‖2≤γ‖ω(t)‖2. □

Remark 3Theorem 1 presents an H∞performance analysis condition of the networked control system with time-varying delays,time-varying sampling intervals and signal transmission deadbands,which is an LMI condition when the controller gain K is given.Theorem 1 describes the relationship between BND,BSI,BTD and the H∞disturbance attenuation level γ.Note that d(t)is a piecewiselinear function and satises˙d(t)=1.We choose a Lyapunov functional with discontinuities at the jump instants (sk+τk,k=0,1,2,3...)which takes full consideration of the characteristic information of the system state x(t) and the derivative of delay term d(t).In the process of calculating the derivative of V(t),we use the delay partitioning approach and a positive scal the interval[t−d(t),t]in terminto two subintervals,that is,[t−d(t),t−αd(t)]and [t−αd(t),t].This can make full use of more information of the state.Moreover,in the proceedings of eliminatingthe integralterms such aswe use the Leibniz-Newton formula and introduce some free weighting matrices to express the links between the terms in the formula.This has the potential to yield less conservative results.

Remark 4The networked control systems(14)and (15)without transmission deadbands naturally become the following NCSs subject to time-varying delays and timevarying sampling intervals:

3.2RobustH∞controller design for the NCSs with transmission deadbands

This section is devoted to solving the problem of H∞controller design for NCSs(14)and(15).The following theorempresentsconditionsfortheexistenceofthedesired controller.

Theorem 2Consider the NCS in Fig.1.For given scalars τm,τM,Tm,TM(0≤τm≤τM≤Tm≤TM), δ1＞0,δ2＞0,0≤α＜1,τM/Tm≤ρ≤1,the closedloop NCSs(14)and(15)are asymptotically stable with an H∞disturbance attenuation level γ if there exist matricesappropriate dimensions,such that

where

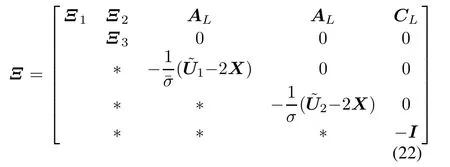
In this case,the state-feedback gain is given by

ProofDene

From(17),we have

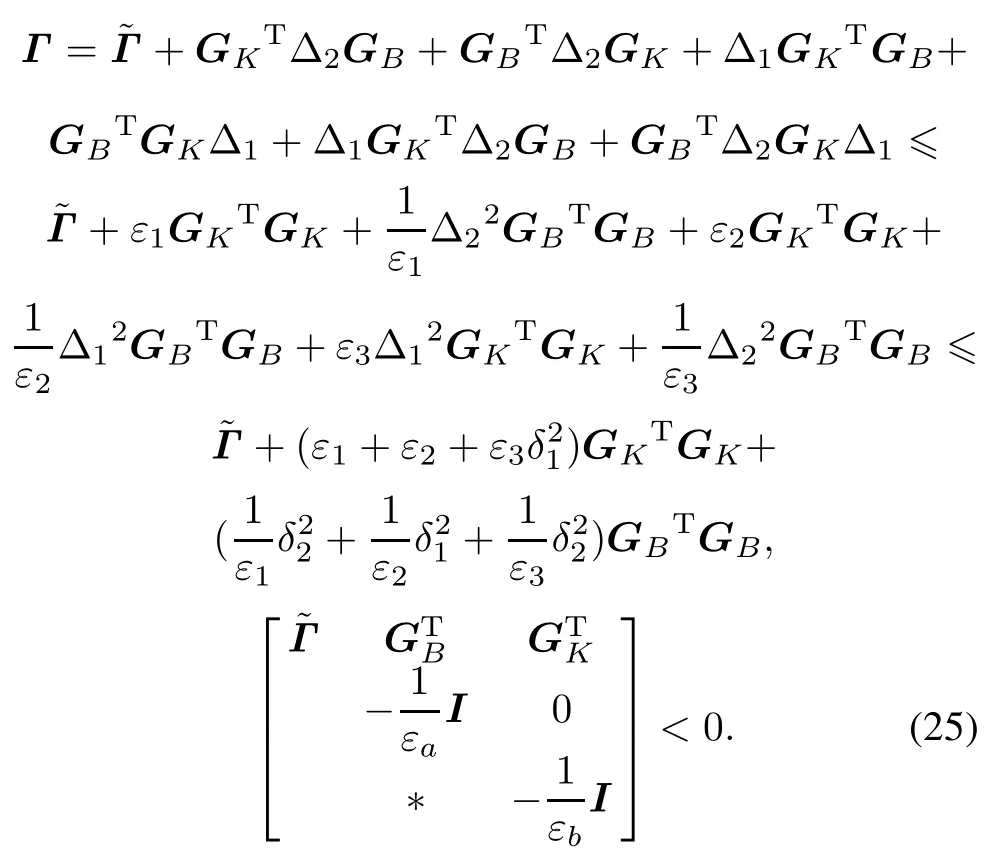
It can be shown that if(17)holds,there exists Γ＜0, that is,˙V(t)＜0 for all sk+τk＜t＜sk+1+τk+1.

Pre-and post-multiplying both sides of(26)by J,and denoting.Then,we have

where

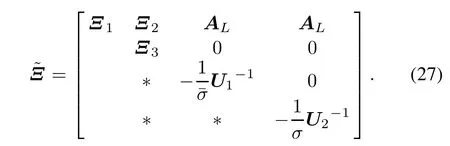
The conditions in above inequality(27)are not LMI because of the nonlinear termsIt is noted thatIn order to solve this non-convex problem,the inequalities in the following are needed.

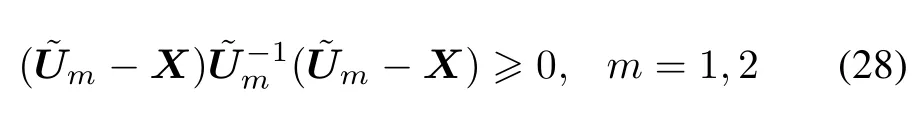
which is equivalent to

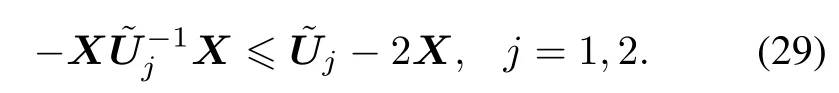
Then,we can obtain(22). □

Remark 5Consider the NCSs(20)and(21)with timevarying delays and sampling intervals.From Theorem 2 (for Δ(K)=0),we can easily obtain the H∞controller design condition of systems(20)and(21).

4.Examples

In the following,three examples will be given to illustrate the effectivenessand applicabilityof the proposedapproaches.

Example 1Consider the following system[25,26]:

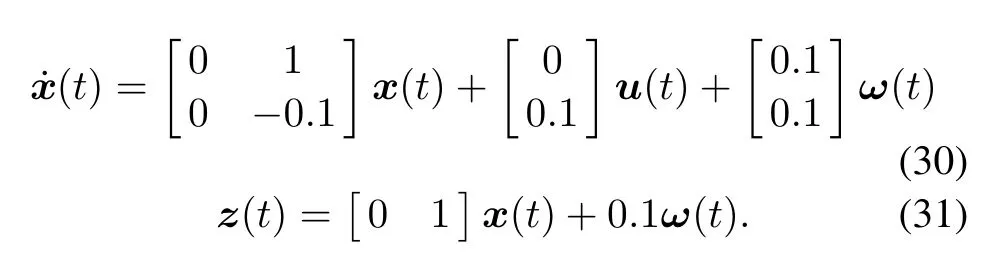
Consider the NCS in Fig.1,wherein no transmission deadbands exist.Choosing the low bound of communication delays τm=0 s,the MAEDB σ=0.869 5 s,by using Remark 5,we can achieve the minimum H∞disturbance attenuation level γ=0.22,while the result in [25]and[26]is γ=1.00.In this case,the controller is K=[−0.000 0−4.615 5].From this example,one can see that this papers provides a less conservative result than [25]and[26].

Example 2Considera simplied modelof the inverted pendulum process[27]as

Consider the NCS in Fig.1,wherein no transmission deadbands exist.Choosing the bounds of communication delays τm=0.1 s,τM=0.15 s,the bounds of sampling intervals Tm=0.18 s and TM=0.48 s,the scalars α=0.36,and ρ=0.85,by using Remark 5,we can achieve the minimum H∞disturbance attenuation level γ=7.703 4.In this case,one can obtain the following solution:

and thestatefeedback controllergain isK = [−0.226 9 −0.074 2].

Example 3Consider the following system[28]:

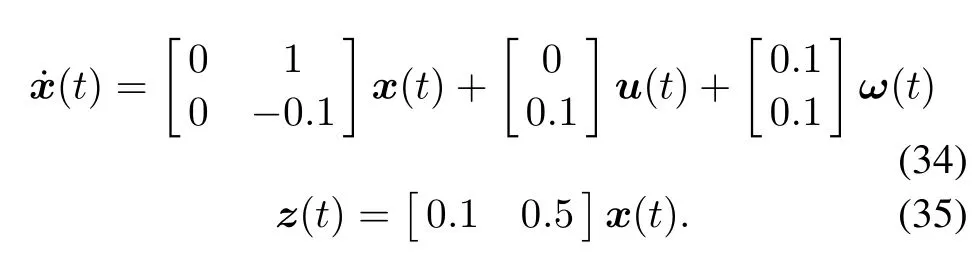
Case 1Consider the NCS in Fig.1,wherein no transmission deadbands exist.Choosing the low bound of communication delays τm=0 s,the MAEDB σ=0.3 s, by using Remark 5,we can achieve the minimum H∞disturbance attenuation level γ=0.051 2,while the result in[28]is γ=0.903 8.In this case,the controller is K=[−3.529 9 −18.439 4].

Case 2Consider the case that there are two transmission deadbands in NCSs.Choosing the bounds of the network-induced delays τm=0 s and τM=0.1 s,the bounds of sampling intervals Tm=0.12 s and TM= 0.2 s,deadband bounds are δ1=0.4 and δ2=0.2,and the scalars α=0.2,ρ=0.9.By using Theorem 3,solving the LMI problem(22),one can obtain the following solution:

Hence,the state feedback controller gain K = ?−2.041 2 −13.099 8?,and the H∞disturbance attenuation level γ=0.656 3.The disturbance signal ω(t) is given as

Fig.2 shows the state response and the control input under deadband control,where the initial state of the NCS is x0=[0,0]T.It can been seen that the closed-loop NCSis asymptotically stable with the above obtained control gain.Table 1 gives the minimum H∞disturbance attenuation level γ for different bounds of the deadband,wherein the bounds of the network-induced delays are chosen as τm=0 s,τM=0.1 s and the bounds of sampling intervals are chosen as Tm=0.12 s and TM=0.2 s.

Fig.2 State response and control input of the closed-loop NCS with two transmission deadbands

Table 1 H∞disturbance attenuation level γ with given τm=0 s, τM=0.1 s,Tm=0.12 s and TM=0.2 s

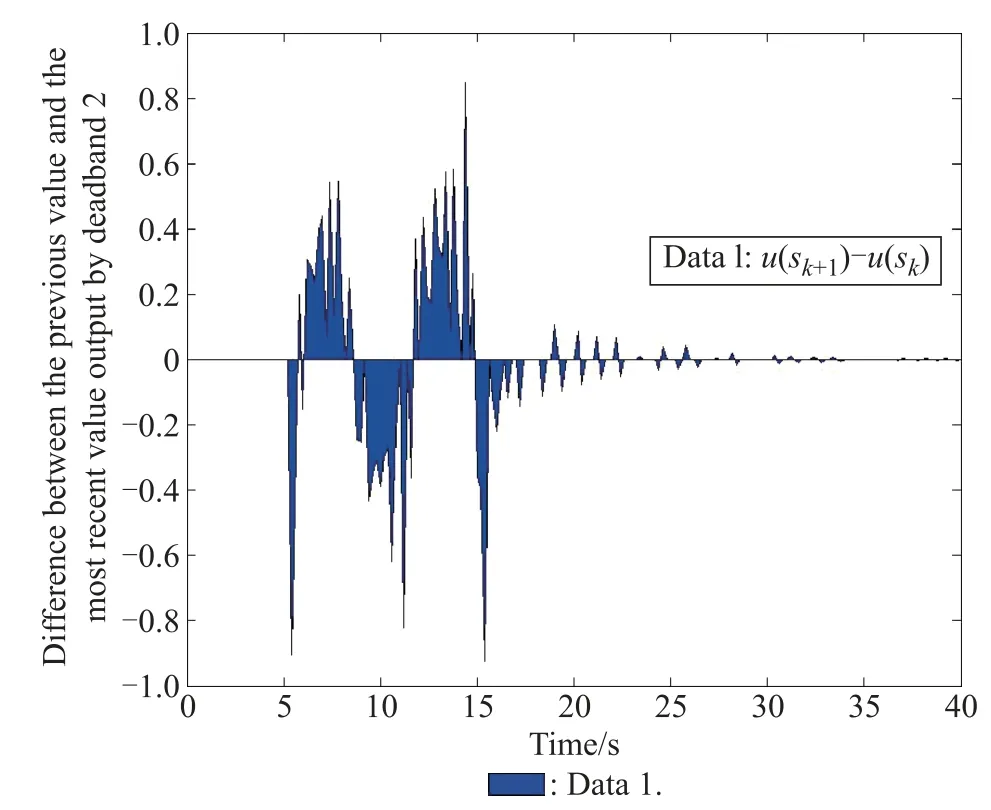
Fig.3 Transmitting situation of the state for δ1=0.2,δ2=0.1

Fig.3 shows the difference between the previous valueand the most recent valueof the output signals from transmission deadband 1 for δ1=0.2 and δ2=0.1,wherein the curve output is not zero,which indicates the state signals are transmitted in the network channel.FromFig.3,it canbefoundtheareaofzeroshows the state signal of the networked systems is not sent in the channel.One can see that the amount of data transmission canbereducedbyadoptingthedeadbandcontrolapproach. Fig.4 shows the output situation of transmission deadband 1 for δ1=0.4 and δ2=0.2.It can be seen that the quantity of data transmission can be reduced more compared to the case of δ1=0.2 and δ2=0.1.

From Fig.4,for the whole simulation time t ranging from 0 s to 40 s,the transmitting time of the state signal mainly focuses on 5 s to 25 s,so,the quantity of the data transmission is about 50%for this time interval.

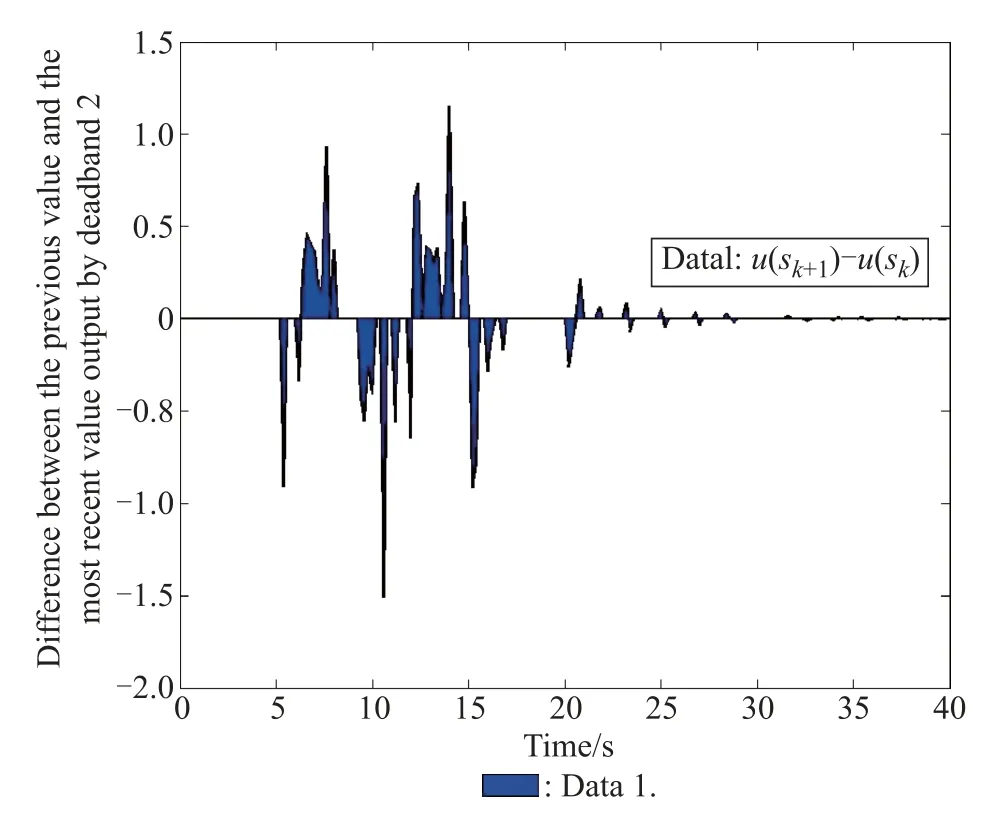
Fig.4 Transmitting situation of the state for δ1=0.4,δ2=0.2

The transmitting situations of the control input signal for δ1=0.2,δ2=0.1 and δ1=0.4,δ2=0.2 have been shown in Fig.5 and Fig.6,respectively.

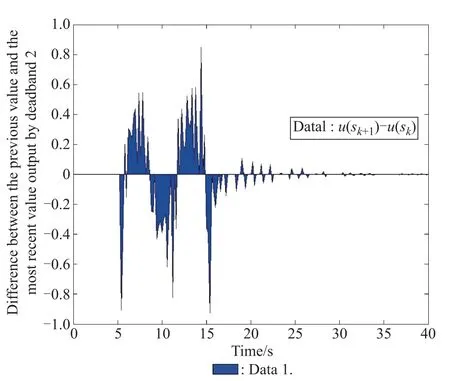
Fig.5 Transmitting situation of the control input for δ1=0.2, δ2=0.1

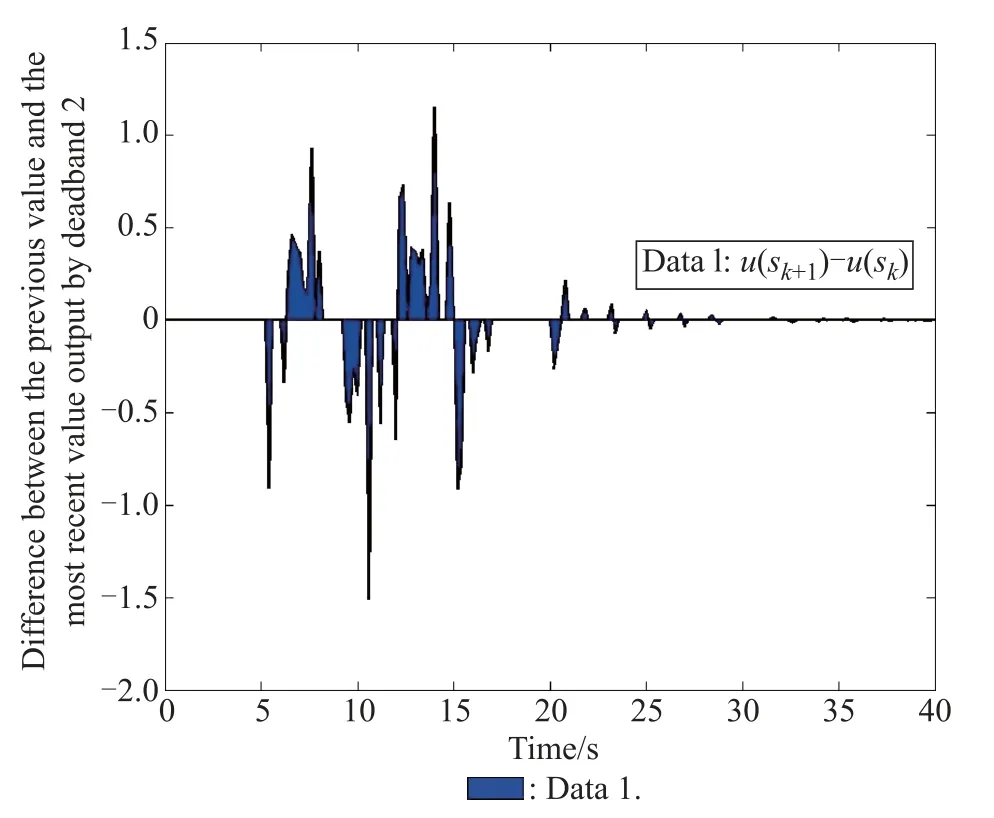
Fig.6 Transmitting situation of the control input for δ1=0.4, δ2=0.2

Notice that the transmitting number of the control input signal for the case δ1=0.4,δ2=0.2 is less than the one of the case δ1=0.2,δ2=0.1.These have shown that the proposed signal difference-based deadband H∞control approach can effectively reduce the data transmission in the network channel,and the designed H∞controller can guarantee the system asymptotically stable and obtain a certain disturbance attenuation level.

5.Conclusions

This paper provides a signal deadband H∞control approach to reduce network data trafc in the view of limited network resources and high network collision in NCSs. Considering network-induced delays,sampling intervals and transmitting deadbands,the NCSs model is presented. By using a Lyapunov-functional approach,a less conservative H∞performance analysis condition of such NCSs is proposed.Moreover,the given deadband H∞controller design condition is in term of LMI.Three examples are usedtoindicatetheeffectivenessofthegivenmethods.The results of simulative experiments show that the data trafc in the NCSs is obviously reduced,and the H∞control performance of the systems is guaranteed by the provided approach.

[1]G.P.Liu,J.Sun,Y.B.Zhao.Design,analysis and real-time implementation of networked predictive control systems.Acta Automatica Sinica,2013,39(11):1769–1776.

[2]J.D.Sun,J.P.Jiang.Delay and data packet dropout separately related stability and state feedback stabilisation of networked control systems.IET Control Theory and Applications,2013, 7(3):333–342.

[3]W.W.Che,J.L.Wang,G.H.Yang.H∞control for networked control systems with limited communication.European Journal of Control,2012,18(2):103–118.

[4]R.N.Yang,P.Shi,G.P.Liu,et al.Network-based feedback control for systems with mixed delays based on quantization and dropout compensation.Automatica,2011,47(12):2805–2809.

[5]Y.Ishido,K.Takaba,D.Quevedo.Stability analysis of networked control systems subject to packet-dropouts andnitelevel quantization.Systems and Control Letters,2011,60(10): 325–332.

[6]F.Rasool,D.Huang,S.K.Nguang.RobustH∞output feedback control of discrete-time networked systems with limited information.Systems and Control Letters,2011,60(10):845–853.

[7]B.Liu,Y.Xia,M.S.Mahmoud.New predictive control scheme for networked control systems.Circuits,Systems,and Signal Processing,2012,31(3):945–960.

[8]H.Li,Z.Sun,H.Liu,et al.Stabilisation of networked control systems using delay-dependent control gains.IET Control Theory and Applications,2012,6(5):698–706.

[9]T.Wang,C.Wu,Y.Wang,et al.Communication channel sharing-based networkinduced delay and packet dropout compensation for networked control systems.IET Control Theory Applications,2013,7(6):810–821.

[10]D.Yue,Q.L.Han,J.Lam.Network-based robustH∞control of systems with uncertainty.Automatica,2005,41(6):999–1007.

[11]J.Dai.A delay system approach to networked control systems with limited communication capacity.Journal of the Franklin Institute,2010,34(7):1334–1352.

[12]H.J.Gao,T.W.Chen,J.Lam.A new delay system approach to network-based control.Automatica,2008,44(1):39–52.

[13]Y.Suh.Stabilityand stabilization of nonuniform sampling systems.Automatica,2008,44(1):3222–3226.

[14]Y.L.Wang,G.H.Yang.H∞controller design for networked control systems via active-varying sampling period method. Acta Automatica Sinica,2008,34(7):814–818.

[15]M.Cloosterman,L.Hetel,N.de Wouwa,et al.Controller synthesis for networked control systems.Automatica,2010, 46(10):1584–1594.

[16]S.Hirche,P.Hinterseer,E.Steinbach,et al.Towards deadband control in networked teleoperation systems.Proc.of International Federation of Automatic Control World Congress,2005.

[17]G.Walsh,H.Ye,L.Bushnell.Stability analysis of networked control systems.IEEE Trans.on Control Systems Technology, 2002,10(3):438–446.

[18]Y.Xu,H.Su,Y.J.Pan.Stability analysis of networked control systems with round-robin scheduling and packet dropouts. Journal of the Franklin Institute,2013,350(8):2013–2027.

[19]K.Liu,E.Fridman,L.Hetel,et al.Stabilityand L2-gain analysis of networked control systems under round-robin scheduling:atime-delayapproach.Systems andControl Letters,2012, 61(5):666–675.

[20]Z.H.Huo,Y.Zheng,C.Xu.A robust fault-tolerant control strategy for networked control system.Journal of Networkand Computer Applications,2011,34(2):708–714.

[21]J.Yook,D.Tilbury,H.Wong,et al.Trading computations for bandwidth:state estimators for reduced communication in distributed control systems.Proc.of the Japan-USA Symposium on Flexible Automation,2000.

[22]P.Otanez,J.Moyne,D.Tilbury.Using deadbands to reduce communication in networked control systems.Proc.of American Control Conference,2002:3015–3020.

[23]Y.B.Zhao,G.P.Liu,D.Rees.Packet-based deadband control for internet-based networked control systems.IEEE Trans.on Control Systems Technology,2010,18(5):1057–1067.

[24]E.Fridman,U.Shaked,V.Suplin.Input/output delay approach to robust sampled-dataH∞control.Systems and Control Letters,2005,54(3):271–282.

[25]X.Jiang,Q.Han,S.Liu,et al.A newH∞stabilization criterion for networked control systems.IEEE Trans.on Automatic Control,2008,53(4):1025–1032.

[26]X.L.Zhu,G.Yang.RobustH∞performance analysis for continuous-time networked control systems.Proc.of American Control Conference,2008,5204–5209.

[27]E.G.Tian,D.Yue.A new state feedbackH∞control ofnetworked control systems withtime-varying network conditions. Journal of the Franklin Institute,2012,349(3):891–914.

[28]J.Wang,H.Yang.H∞control of a class of networked control systems with time delay and packet dropout.Applied Mathematics and Computation,2011,217(18):7469–7477.

Biographies

Yingying Liu received her B.S.and M.S.degrees in Shenyang University of Technology,China,in 2003 and 2006,respectively,and Ph.D.degree in control theorem and control engineering from Northeastern University,China,in 2011.She is currently a lecturer at the College of Information Engineering,Shenyang University.Her research interests include networked control systems and time delay systems.

E-mail:lyy3636@163.com

Weiwei Che received her Ph.D.degree in control engineering from Northeastern University,China,in 2008.She joined the EEE of Nanyang Technological University from 2008 to 2009 as a postdoctoral fellow.She is currently an associate professor of Shenyang University.Her research interests include non-fragile control,quantization control and their applications to networked control system design.

E-mail:cwwemail1980@126.com

Yunkai Chu received his B.S.and M.S.degrees in Shenyang University of Technology,China,in 2003 and 2006,respectively.He is currently an assistant researcher at Shenyang Institute of Automation of Chinese Academy of Sciences.His research interests include automatic-controlelds such as automobile and aviation industries.

E-mail:chuyunkai@sia.cn

10.1109/JSEE.2015.00065

Manuscript received March 15,2013.

*Corresponding author.

This work was supported by the National Natural Science Foundation of China(61104106;61473195),the Natural Science Foundation of Liaoning Province(201202156),and the Program for Liaoning Excellent Talents in University(LJQ2012100).