Control synthesis of linear distributed parameter switched systems

Leping Bao,Shumin Fei,and Lin Chai

1.School of Automation,Southeast University,Nanjing 210096,China;

2.Department of Automation,Taiyuan Institute of Technology,Taiyuan 030008,China

Control synthesis of linear distributed parameter switched systems

Leping Bao1,2,∗,Shumin Fei1,and Lin Chai1

1.School of Automation,Southeast University,Nanjing 210096,China;

2.Department of Automation,Taiyuan Institute of Technology,Taiyuan 030008,China

The control synthesis for switched systems is extended to distributed parameter switched systems in Hilbert space.Based on semigroup and operator theory,by means of multiple Lyapunov method incorporated average dwell time approach,sufcient conditions are derived in terms of linear operator inequalities framework for distributed parameter switched systems.Being applied to one dimensional heat propagation switched systems,these linear operator inequalities are reduced to linear matrix inequalities subsequently.In particular,the state feedback gain matrices and the switching law are designed,and the state decay estimate is explicitly given whose decay coefcient completely depends on the system’s parameter and the boundary condition.Finally,two numerical examples are given to illustrate the proposed method.

distributed parameter switched systems,multiple Lyapunov method,stabilization,linear operator inequalitie,average dwell time.

1.Introduction

During the last decade,the study of switched systems has attracted increasing attention because of its signicance in both theoretical research and practical applications[1–13].A switchedsystem is adynamicalsystemthatincludes a family of subsystems and a logical rule generates switching signals(law)between these subsystems at each instant of time.It is pointed out that there are three basic problemsinstabilityanalysisandcontrolsynthesisforswitched systems:(i)tond the conditions for stability(stabilizing)under arbitrary switching law;(ii)to identify the stability(stabilizing)switching signals;and(iii)to construct a stability(stabilizing)switching signal[3].Many efcient approaches have been developed to deal with these three basic problems in the existing literature.Among them, average dwell time has been shown as an effective technique[5,10,11].

On the other hand,there are several works concerning with distributed parameter switched systems(DPSS) whichare describedby partial differentialequations(PDE) or a combination of ordinary differential equations(ODE) andPDE[12–24].For example,Amol et al.used the common Lyapunovfunction approachto investigateinnite dimensional switched systems under arbitrary switching law [15,19,20].El-Farra used Galerkin’s method(the system is reducedto anite-dimensionalmodel)to controlsynthesis for quasi-linearparabolic equationin which the state equation isxed and the controller is switched[14].Ouzahra consideredfeedbackstabilizationofxeddistributedsemilinear systems using switching controls which did not requiretheknowledgeofthestate ofthesystem[24].Mostly, the existing works relating to DPSS concentrate on problem(i)[15,19–21].Muchfewerresults havebeenreported on the problem(ii)[22,25,26]and problem(iii)for DPSS. Problem(ii)is concerned withnding stability(stabilizing)switching signals on the condition that all the individual subsystems of the switched systems are stable,and we know that dwell time and average dwell time are two effective methods to specify slow switching of the switching law.However,it is worth mentioning that,up to now,little effort has been devoted to stability analysis and control synthesis by using average dwell time scheme for DPSS [26].

Motivated by the above considerations,in this paper, based on semigroup and operator theory,we investigate the exponential stabilization of DPSS via multiple Lyapunov function that incorporates average dwell time approach.The main idea using semigroup and operator theoryis that theyplaya centralrole andprovidea uniedand powerfultool for the study of PDE systems[27].The main contribution of this paper is as follows.Firstly,under the average dwell time switching rule,the stabilization condi-tions for the overall distributed parameterswitched control system are established in terms of linear operator inequalities(LOIs)framework,which is differentfromthe existing work on DPSS.Due to the multiple variable,the behavior of switched heat propagation systems is much more complicated than that of the ODE switched systems.It is difcult to transform the innite dimensional LOIs into thenite dimensional linear matrix inequalities(LMIs).Here, we use Wirtinger’s inequality to overcome the difculty. Secondly,being applied to one dimensional heat propagationswitchedsystem,these LOIsarereducedto LMIs.Particularly,the state feedback gain matrices and the switching law are designed by using Matlab software,and the state decay estimate is explicitly given for DPSS whose decay coefcient completely depends on the system’s parameter and the boundary condition.Finally,two numerical examples are presentedto illustrate the proposedresult.

The rest of this paper is organized as follows.In Section 2,some preliminary works and problem formulation are given.Section 3 investigates control synthesis for DPSS determined by semigroups.The one dimensional switched heat equations are applied in Section 4 andnumericalexamplesaregiventoillustratetheproposed method in Section 5.Conclusions are summarized in Section 6.

2.Preliminaries and problem formulation

Throughout this paper,let R=(−∞,+∞),R+= [0,+∞).Rndenotes the n-dimensional Euclidean space with the norm|·|.For a real n×n matrix Q(i.e.Q ∈Rn×n),notation Q ＞0 means that Q is symmetric and positive denite.λmax(Q)(λmin(Q))denotes the maximum(minimum)eigenvalue of the matrix Q.Let I stand for the identity operator on H or appropriate dimensional identity matrix in different situation.The superscript“T”represents matrix transposition.

Let H be a Hilbert space equipped with the inner product〈·,·〉,‖·‖denote the norm.In this case,the norm of x∈H is given by‖x‖=〈x,x〉12.Let L(U,H)denote the space of bounded linear operator from U to H,L(H) denote the space of bounded linear operator from H to H.

C([a,b],H)denotes the space of the continuous H-value functions x:[a,b]→ H with the induced norm

C1([a,b],H)denotes the space of continuously differentiable H-value functions x: [a,b] →H with the induced norm ‖x‖C1([a,b],H)= max(‖x‖C([a,b],H),‖˙x‖C([a,b],H)).

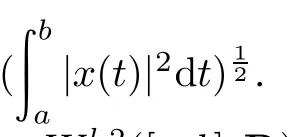
Wl,2([a,b],R)is the Sobolev space of absolutely continuous scalar functions on[a,b]with square integrable derivatives of the order l≥1.

Defnition 1[28]Let P:H→H with a densedomain D(P)⊂H be self-adjoint,then P≥0(positive)if

whereasP＞0(strictly positive),iff it is self-adjointin the sense that P∗=P and there exists a constant m＞0,such that

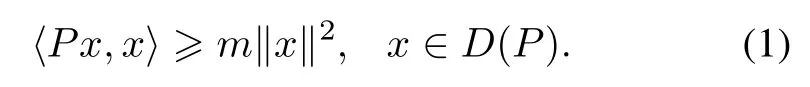
Defnition 2[28] An operator M ∈L(H)is called invertible if there exists an operator N∈L(H),such that MN=NM=I.We write N=M−1to denote the inverse of operator M.

Lemma 1[29]Wirtinger’s inequalities

Let z ∈ W1,2([a,b],R)be a scalar function with z(a)=z(b)=0.Then

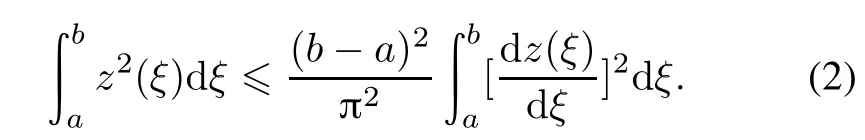
If additionally z∈W2,2([a,b],R),then

In this paper,we consider a general form of linear switched control systems determined by semigroup:

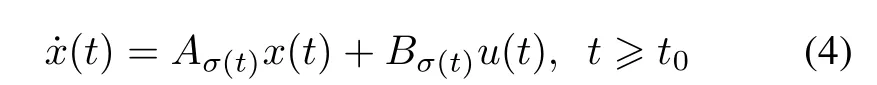
with the initial condition

where x∈H is the state of the system,u∈U is the control.σ:R+=[0,∞)→ Θ is the switching signal mapping time to anite index set,Θ={1,2,...,m}. The switching signal σ is a piecewise continuous(fromthe right)functiondependingon time or state or both.The discontinuities of σ are called switching times or switching instants.m is the number of models(called subsystems) of the switched system.Aiare innitesimal generator of semigroup Ti(t)(i∈Θ)respectively,and Biare operators.

The switching signal σ can be characterized by a switching sequence(called switching law):

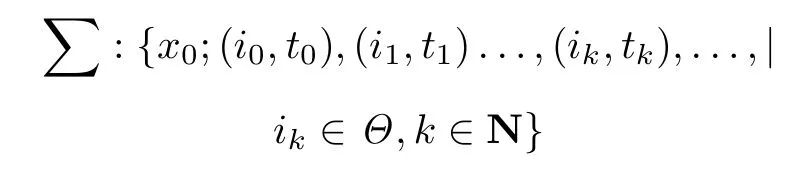
in which t0is the initial time,x0is the initial state and N is the set of nonnegative integers.Switching time t0＜when t∈ [tk,tk+1),σ(t)=ik,that is,the ikth subsystem is active.Therefore,the trajectory x(t)of the switched system(4)is the trajectory of the ikth subsystem when t∈[tk,tk+1).

The objective of this paper is to design state feedback control

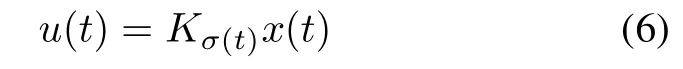
and a switching law.Ensuring exponentially stabilize the overall closed-loop DPSS

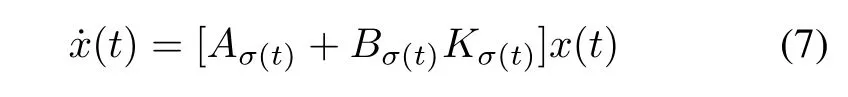
where K1,K2,...,Kmare a family of gain operators to be determined.

Defnition 4[6]DPSS(4)and(5)are said to be state feedback exponentiallystabilizable,if there exist a switching signal σ,and a piecewise linear state feedback control input(6)such that the closed-loop switched system(7)is exponentially stable.

Defnition 5DPSS(4)and(5)can be exponentially stabilized by the state feedback controller(6)at the equilibrium point 0 under switching signal σ(t)if there exist constants K≥1 and γ＞0,such that the solution x(t)of close-loop systems(5)and(7)satises

3.Control synthesis for DPSS determined by semigroup

It is a common fact that even when all the subsystems are stable,the switched system(whether it is governed by ODE or PDE)may be unstable for certain switching signals[1,3,20,22].It is also known that a switched system is stable if all individual subsystems are stable and the switching is sufciently slow,so as to allow the transient effects to dissipate after each switch[1].In this section,we discuss how the exponential stabilization property can be preserved for DPSS in Hilbert space by using semigroup.

Without loss of generality,we make the following assumptions.

Assumption1[1](i)Thereis nostatejumpataswitching instant,i.e.,the trajectory x(t)is everywhere continuous.(ii)σ has anite number of switching on anynite interval of time,that is,there is no Zeno behavior.

Assumption 2(i)Operator Ai(i∈ Θ)generates a strongly continuous semigroup Ti(t)and the domain D(Ai)⊂H of the operatorAiis dense in H.(ii)Operator Bi∈L(U,H)and Ki∈L(H,U).(iii)x0∈H.

Given ϕ(·,t0,x0)denote the solution of closed-loop DPSS(7),for every function Vi∈C(H×[t0,+∞),R+), we dene the upper right-hand derivative of Vi[30]with respect to t along the solution of system(7)as follows:

Choose the multiple Lyapunovfunctioncandidateof the form

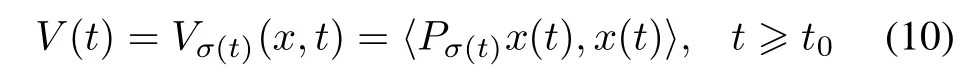
for the closed-loop system(7)in corresponding Hilbert space D(Ai)(i∈Θ),where Pσ(t)is switched in accordance with the piecewise constant switching signal σ(t).Assumption 3Operators Pi:D(Ai)→H satisfying

for some positive constants γpi,γPi.

Theorem 1Consider systems(4)and(5)under the state feedback control(6),for given constant β＞0,suppose that Assumptions 1 and 2 are satised,if there exist operators Pi＞0,subject to(11)such that the following operator inequalities

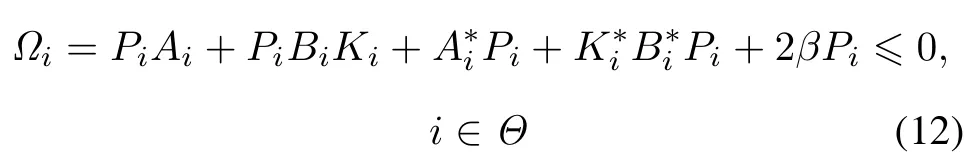
holdin the Hilbert space D(Ai)(i∈Θ)in the sense of(1), and there exists a constant μ≥1 such that the Lyapunov function(10)satises

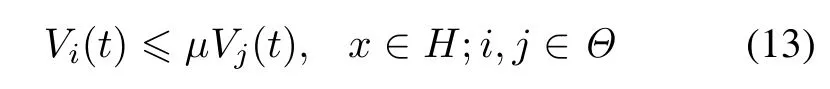
Moreover,a state decay estimate for closed-loop systems(5)and(7)is given by

ProofSuppose Assumptions 1 and 2 hold,it can be proved that systems(5)and(7)have a unique mild solution for every x0∈H.i.e.,systems(5)and(7)turn to be well-posed on time interval[t0,∞)because the state does not jump at the switching instants.(see,e.g.[31]for details)

Choosethe multiple Lyapunovfunctioncandidateas the form of(10)for system(7)in the Hilbert space D(Ai)(i= 1,2,...,m),where operatorsPi＞0 satisfy(11)and(12).

Similar to the proof of Theorem 1 in[26],it is not difcult to obtain

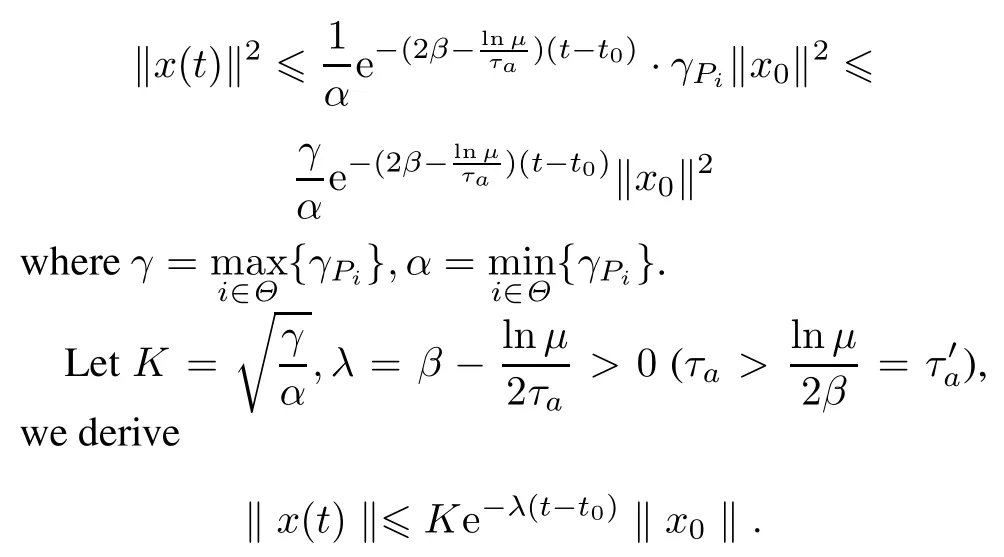
Theorem 2Consider systems(4)and(5)under the state feedback control(6),for given constant β＞0,assumethat the conditionsin Theorem1 aresatised,if there exist linear operators Xi＞0 and Yisuch that the following LOIs:

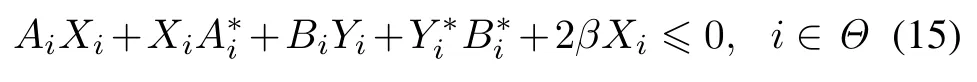
hold in the Hilbert space D(Ai)in the sense of(1),whereL(H)).Then the overall DPSS(4)and(5)can be exponentially stabilized by the state feedback controller(6)for arbitrary switching signal σ(t)with average dwell time satisfying τa＞

ProofThe equivalence between(12)and(15)can be easily shown by left-and right-multiplying

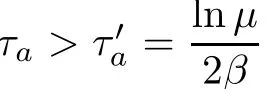
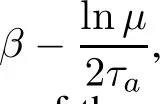
4.Application to one dimensional heat propagation switched systems

Consider the following switched one dimensional heat propagation equations:

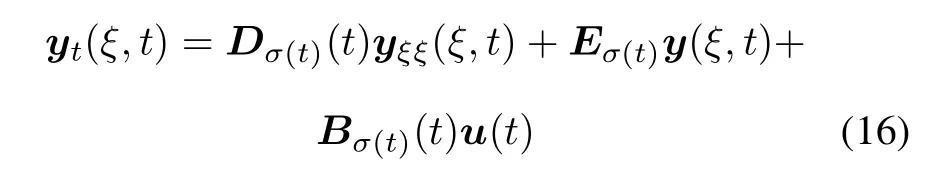
with the initial value

and the boundary condition

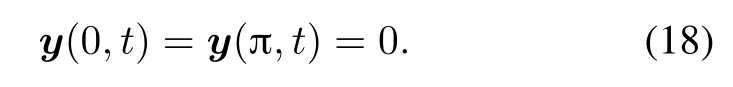
We are interesting in designing the static state feedback

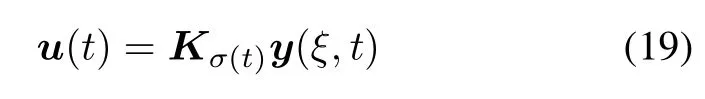
and a switching law such that the overall closed-loop system

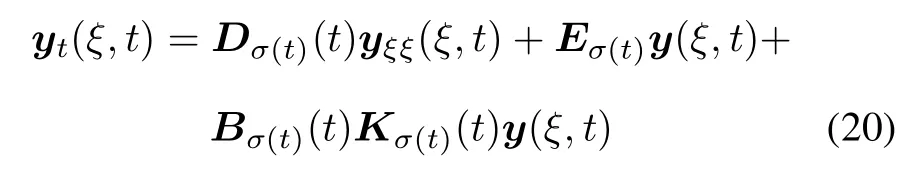
is exponentially stabilizable.

Where y=(y1,y2,...,yn)∈Rnis an n-dimensional state vector(the“state”vector of the system),u = (u1,u2,...,ul)∈Rlis an l-dimensional control vector (the“control”),y depends on spatial variable ξ and time variable t,0≤ξ≤π,t≥t0.Diare positive constants. Bi,Ei(i=1,2,...,m)are known appropriate dimensional constant matrices,Kiare family of gain matrices to be determined.

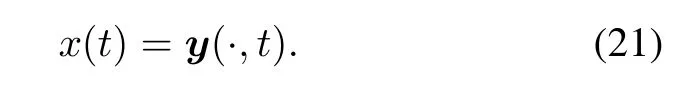
Then the system(20)has the form of system(7)in Hilbert space H with the operators A1,A2,...,Amas A1=Emhave the domain

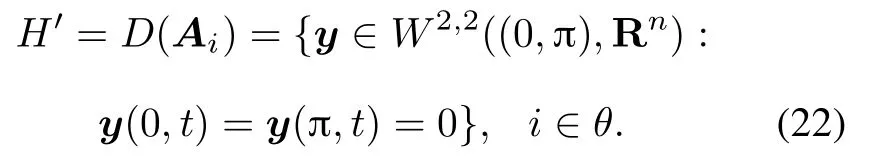
It is known that the operators A1,A2,...,Amgenerate analytical semigroups T1(t),T2(t),...,Tm(t)respectively.Foreveryinitialvaluey0∈H′,thereexistsaunique classical solution for system(20)(see,e.g.,[29]for details).

Choose the multiple Lyapunov function

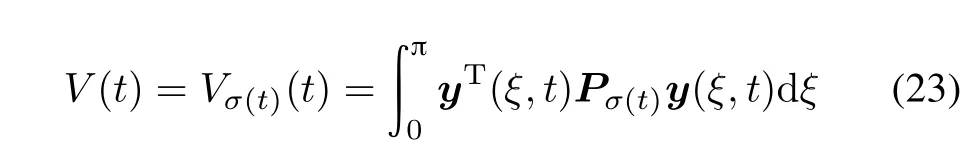
with positive constant symmetric matrices Pi. Differentiating(23),wend that

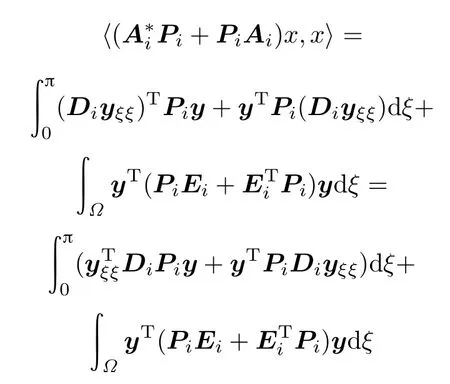
hold for x∈H′.

BecauseDiareconstants,weknowthatPiDi=DiPi.

Integrating by parts,we have

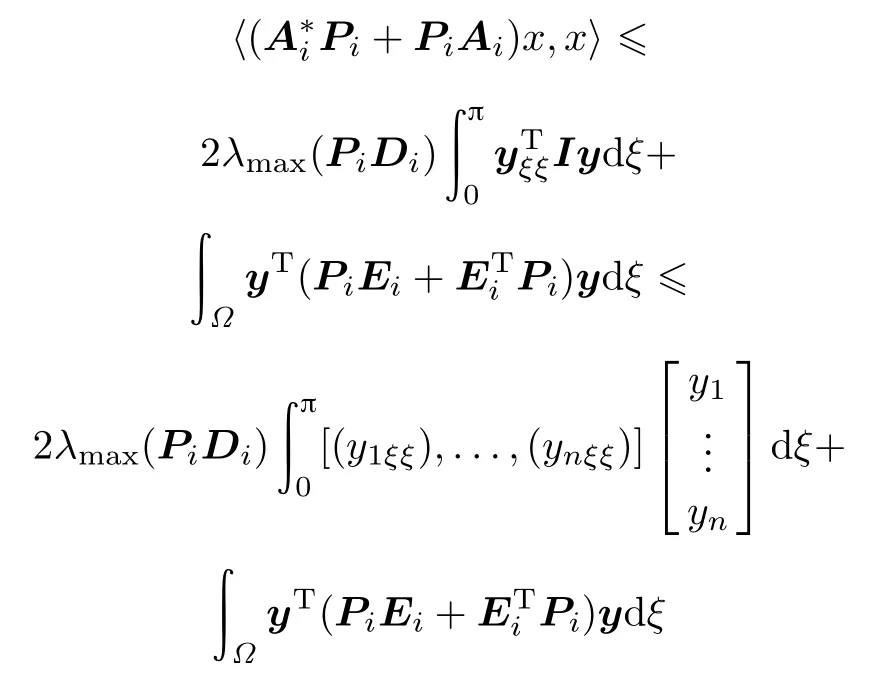
hold in H′.

CombiningWirtinger’sinequality(2)andtakingintoaccount the boundary condition(18)result in the following inequalities

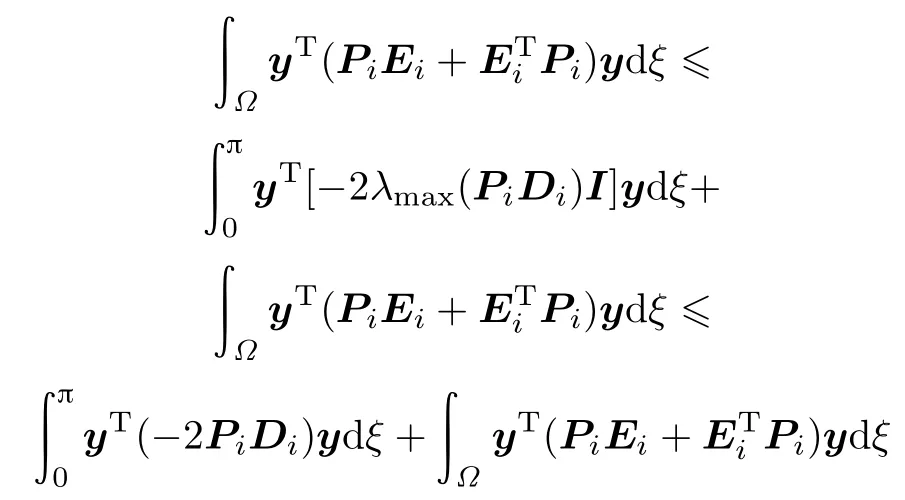
We have

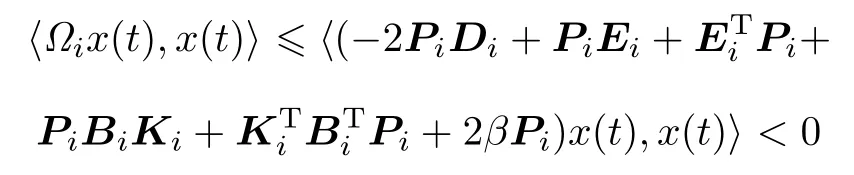
Provide that the following LMIs

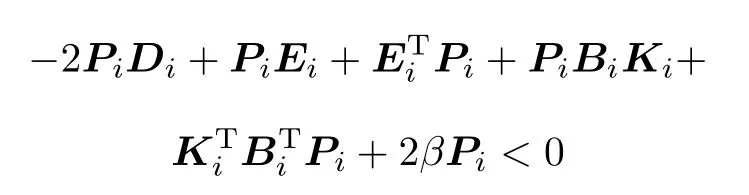
Furthermore,the inequalities(13)hold,then we can conclude the following result.

Theorem 3Consider systems(16)–(18)under the state feedback controller(19),for given constant β＞0, if there exist symmetric matrices Pi＞0 and a set of feedback matrices Ki(i=1,...,m),such that the following inequalities

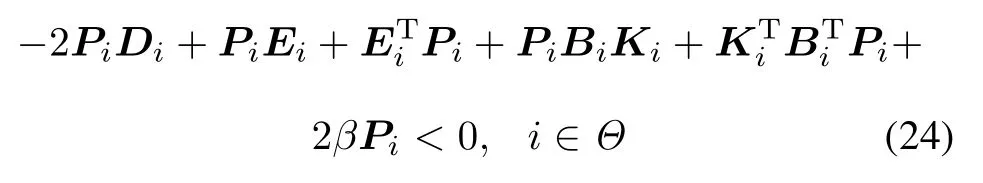
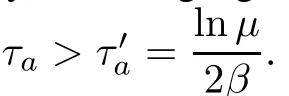
Moreover,a state decay estimate for closed-loopsystem (20)is given by

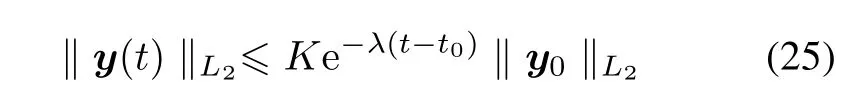
In the following,we transform inequalities(24)into LMIs which can be solved by the Matlab software.By the similar argument that used in Theorem 2,we obtain the following theorem which is the main result of the present paper.

Theorem 4Consider systems(16)–(18)under the state feedback controller(19),for given constant β＞0,if there exist symmetric matrices Xi＞0 and matrices Yi, such that the following LMIs

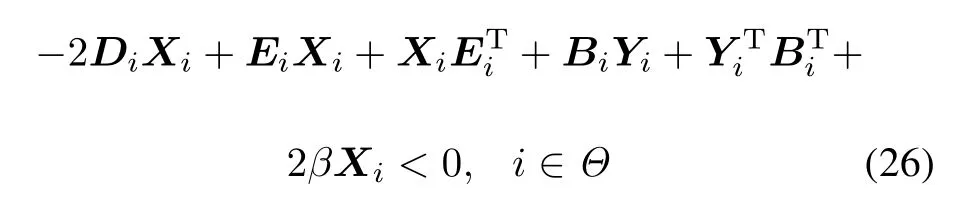
are feasible,and there exists a constant μ≥1 such that the inequalities(13)hold,whereThen the overall DPSS(16)–(18)can be exponentially stabilized by state feedback controller(19)for arbitrary switching signal σ(t)with average dwell time satisfying

Moreover,a state L2norm estimate for closed-loopsystem(20)is given by(25).

Remark 3The idea of applying LOIs to the study of distributed parameter systems has appeared in[32,33].As is shown,these LOIs are subsequently reduced to standard LMIs,which provides a new insight into the control theoryofdistributedparametersystems.Inspiredbytheabove works,here,we utilize LOIs framework to innite dimensional switched systems,and generalize the stability result of ODE switched systems[5]to DPSS.

Remark 4Compared with the existing work in[21],it should be pointed out that the advantagein this work is our stabilization conditions completely depend on the system’parameterandboundarydata.Ontheotherhand,compared with the existing works without considering switching in [32],the switching system we consider here is fairly general in which the system is matrix distributed parameter system.

5.Illustrative examples

In this section,we give two numerical examples to illustrate the proposed method.

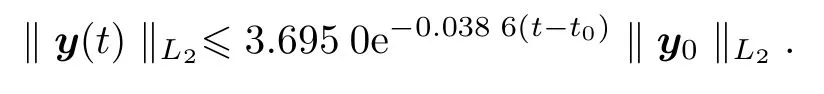
Let system(20)start with initial condition for(y1,y2)= (1.6,0.9),ξ∈[0,π],the exponential bound of(20)with L2norm under average time τa=5 is shown in Fig.1.

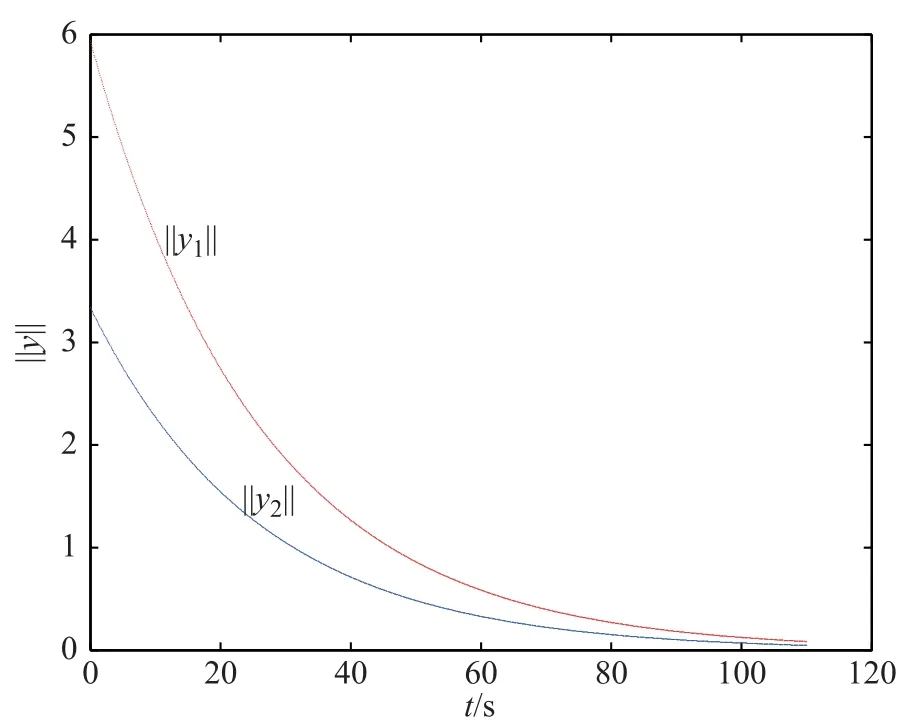
Fig.1 Exponential bound of‖ y(t)‖L2under average time τa=5

Example 2Consider switched heat propagation equation(16)–(18)with state feedback control(19),and let

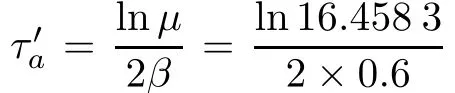
Using Theorem 4,by resolving LMI(26),we obtain the state feedback matrices

The state decay for closed-loop DPSS(20)is given by

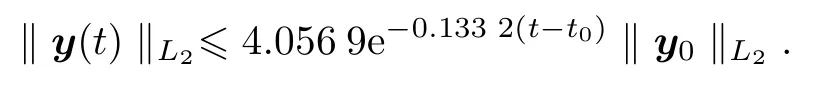
For example 2,if the initial condition is as the same as that of in Example1,we plot the exponentialboundof system(20)with L2norm in Fig.2.

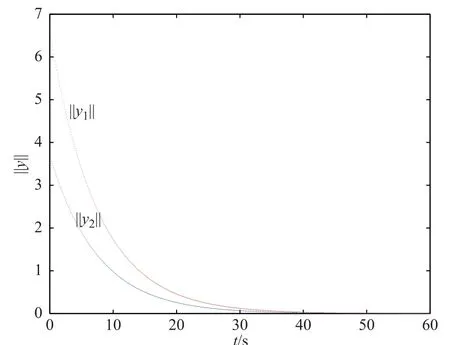
Fig.2 Exponential bound ofin Example 2 obtained in Theorem 4

6.Conclusions

In this paper,based on semigroup and operator theory, some sufcient conditions of exponential stabilization for a class of linear DPSS are developed in a LOIs framework that incorporates with average time scheme.Being applied toswitchedheatpropagationequations,wetransformLOIs into LMIs which has the advantage of being numerically well tractable by using Matlab software and the state decay estimate is explicitly given for DPSS.In particular,the state feedback controller and switching law have also been designed.Finally,two examples are given to illustrate the proposed method.

[1]D.Liberzon.Switching in systems and control.Boston,MA: Birkhauser,2003.

[2]Z.Sun,S.S.Ge.Switched linear systems:control and design. Berlin:Springer-Verlag,2004.

[3]D.Liberzon,A.S.Morse.Basic problems in stability and design of switched systems.IEEE Control System Magazine, 1999,19(10):59–70.

[4]J.P.Hespanha,A.S.Morse.Stabilityof switched systems with average dwell time.Proc.of the American Control Conference, 1999:2655–2660.

[5]G.Zhai,B.Hu,K.Yasuda,et al.Piecewise Lyapunov functions for switched systems with average dwell time.Asian Journal Control,2000,2(3):192–197.

[6]Z.Sun,S.S.Ge.Switched stabilization of higher-order switched linear systems.Proc.of the 44th IEEE Conference on Decision and Control,2005.

[7]L.Zhang,C.Wang,H.Gao.Delay-dependent stabilityand stabilization of a class of linear switched time-varying delay systems.Journal of Systems Engineering and Electronics,2007, 18(2):320–326.

[8]H.Lin,P.J.Antsaklis.Stability and stabilizability of switched linear systems:a survey of recent results.IEEE Trans.on Automatic Control,2009,54(2):308–322.

[9]J.Lin,S.Fei,J.Shen.Robust stability and stabilization for uncertain discrete-time switched singular systems with timevarying delays.Journal of Systems Engineering and Electronics,2010,21(4):650–657.

[10]X.M.Sun,J.Zhao,D.J.Hill.Stability and gain analysis for switched delay systems:a delay-dependent method.Automatica,2006,42(10):1769–1774.

[11]W.A.Zhang,L.Yu.Stability analysis for discrete-time switched time-delay systems.Automatica,2009,45(10): 2265–2271.

[12]X.Li,Z.R.Xiang,H.R.Karimi.Asynchronously switched control of discrete impulsive switched systems with time delays.Information Sciences,2013,249(1):132–142.

[13]M.Xiang,Z.R.Xiang.Stability,L1-gain and control synthesis for positive switched systems with time-varying delay.Nonlinear Analysis:Hybrid Systems,2013,9(1):9–17.

[14]N.H.El-Farra,P.D.Christodes.Coordinating feedback and switching for control of spatially distributed processes.Computers and Chemical Engineering,2004,28:111–128.

[15]A.Sasane.Stabilityof switching innite-dimensional systems. Automatica,2005,41(1):75–78.

[16]A.N.Michel,Y.Sun,A.P.Molchanov.Stability analysis of discontinuous dynamical systems determined by semigroups. IEEE Trans.on Automatic Control,2005,50(9):1277–1290. [17]A.N.Michel,Y.Sun.Stability of discontinuous cauchy problems in Banach space.Nonlinear Analysis,2006,65:1805–1832.

[18]O.V.Iftime,M.A.Demetriou.Optimal control of switched distributed parameter systems with spatially scheduled actuators.Automatica,2009,45(2):312–323.

[19]F.M.Hante,M.Sigalotti.Existence of common Lyapunov functions for innite-dimensional switched linear systems. Proc.of the 49th IEEE Conference on Decision and Control, 2010.

[20]F.M.Hante,M.Sigalotti.Converse Lyapunov theorems for switched systems in Banach and Hilbert spaces.SIAM Journal on Control and Optimization,2011,49(2):752–770.

[21]X.Dong,R.Wen,H.Liu.Feedback stabilization for a class of distributed parameter switched systems with time delay.Journal of Applied Sciences-Electronics and Information Engineering,2011,29(1):92–96.

[22]S.Amin,F.Hante,A.Bayen.Exponential stability of switched linear hyperbolic initial-boundary value problems. IEEE Trans.on Automatic Control,2012,57(2):291–301.

[23]F.Castillo,E.Witrant,C.Prieur,et al.Dynamic boundary stabilization of hyperbolic systems.Proc.of the 51th IEEE Conference on Decision and Control,2012.

[24]M.Ouzahra.Global stsbilization of semilinear systems using switching controls.Automatica,2012,48(2):837–843.

[25]Y.P.Luo,W.H.Xia,G.R.Liu,et al.An LMI approach to expontienal stabilizationofdistributedparameter control systems with delay.Acta Automatica Sinica,2009,35(8):299–304.

[26]L.P.Bao,S.M.Fei,L.Yu.Exponential stability of linear distributed parameter switched systems with time-delay.Journal of Systems Science and Complexity,2014,27(2):263–275.

[27]N.U.Ahmed.Semigroup theory with applications to system and control.New York,MA:Longman Scientic Technical, 1991.

[28]M.Tucsnak,G.Weiss.Observation and control for operator semigroups.Basel:Birkhauser Verlag,2009.

[29]T.X.Wang.Stability in abstract functional differential equations.Part II.Applications.Journal of Mathematical Analysisand Applications,1994,186:835–861.

[30]A.N.Michel,L.Hou.Stability of dynamical system.New York,MA:Springer,2008.

[31]R.F.Curtain,H.Zwart.An introduction to infnite dimensional linear system theory.New York,MA:Springer,1995.

[32]E.Fridman,Y.Orlov.Exponential stability of linear distributed parameter systems with time-varying delays.Automatica,2009,45(1):194–201.

[33]Z.Tai,S.Lun.Absolute mean square exponential stability of Lur’e stochastic distributed parameter control systems.Applied Mathematics Letters,2012,25:115–119.

Biographies

Leping Bao was born in 1968.She received her M.S.degree in the Department of Mathematics from Guizhou University in 2006,the Ph.D.degree in control theory and control engineering from Southeast University in 2014.She is now a lecture in the Department of Automation,Taiyuan Institute of Technology.Her main research direction is distributed parameter switched systems.

E-mail:jsll68@126.com

ShuminFei was bornin 1961.He received hisPh.D. degree from Beihang University in 1995.He is now a professor in the School of Automation,Southeast University.His research interests include nonlinear systems,robust control,adaptive control,and distributed parameter switched systems.

E-mail:smfei@seu.edu.cn

Lin Chai was born in 1978.She is now an associate researcher in the School of Automation,Southeast University.Her research interests include nonlinear systems,robust control,and adaptive control.

E-mail:chailin1@seu.edu.cn

10.1109/JSEE.2015.00064

Manuscript received November 04,2013.

*Corresponding author.

The work was supported by the National Natural Science Foundation of China(61273119;61374038;61473079;61473083),and the Natural Science Foundation of Shanxi Province(2012011002-2).