Bayesian optimal design of step stress accelerated degradation testing

Xiaoyang Li,Mohammad Rezvanizaniani,Zhengzheng Ge, Mohamed Abualiand Jay Lee

1.Science and Technology on Reliability and Environmental Engineering Laboratory,Beihang University,Beijing 100191,China;

2.NSF Industry/University Cooperative Research Center on Intelligent Maintenance Systems, University of Cincinnati,OH 45221,USA;

3.Beijing Institute of Electronic System Engineering,Beijng 100854,China

Bayesian optimal design of step stress accelerated degradation testing

Xiaoyang Li1,*,Mohammad Rezvanizaniani2,Zhengzheng Ge3, Mohamed Abuali2and Jay Lee2

1.Science and Technology on Reliability and Environmental Engineering Laboratory,Beihang University,Beijing 100191,China;

2.NSF Industry/University Cooperative Research Center on Intelligent Maintenance Systems, University of Cincinnati,OH 45221,USA;

3.Beijing Institute of Electronic System Engineering,Beijng 100854,China

This study presents a Bayesian methodology for designing step stress accelerated degradation testing(SSADT)and its application to batteries.First,the simulation-based Bayesian design framework for SSADT is presented.Then,by considering historical data,specic optimal objectives oriented Kullback–Leibler (KL)divergence is established.A numerical example is discussed to illustrate the design approach.It is assumed that the degradation model(or process)follows a drift Brownian motion;the acceleration model follows Arrhenius equation;and the corresponding parameters follow normal and Gamma prior distributions.Using the Markov Chain Monte Carlo(MCMC)method and WinBUGS software,the comparison shows that KL divergence is better than quadratic loss for optimal criteria.Further,the effect of simulation outliers on the optimization plan is analyzed and the preferred surfacetting algorithm is chosen.At the end of the paper,a NASA lithium-ion battery dataset is used as historical information and the KL divergence oriented Bayesian design is compared with maximum likelihood theory oriented locally optimal design.The results show that the proposed method can provide a much better testing plan for this engineering application.

accelerated testing,Bayesian theory,KL divergence, degradation,optimal design,battery.

1.Introduction

The acceleration degradation testing(ADT)technique is commonlyusedtoobtaindegradationdataofproductsover a short time period,to help extrapolate lifetime and reliability under usage conditions.Constant stress accelerated degradation testing(CSADT)and step stress ADT (SSADT)are the two types of ADT that are commonly performed.In CSADT,the samples are divided into different groups and each group is tested under different constant stress levels.For SSADT,all samples are tested with same stress conditions to begin with and the stress levels increase with time.SSADT has the advantages of smaller sample size and shorter testing time than CSADT.Researchon SSADT has rapidlyincreasedin the past decades [1–3].

Traditional optimal design of SSADT is based on a known degradation model and specied values of model parameters.If the deviation between the specied value andthetruevalueislarge,anoptimaltestingplanis usually hard to obtain.Consequently,the plan will not provide the most effective testing data.If prior information or similar data of products are available before testing,the design of SSADT using the Bayesian method will be more reliable and efcient than using the traditional method.

Park et al.[1]tested designs for SSADT with destructive performance measurements.Based on the cumulative effects of exposure,they established a degradation model withlognormaldistributionanda constantdegradationrate for the performance.They minimized the asymptotic variance of the maximum likelihood estimator of the 100th percentile of the lifetime distribution under the usage condition.Then,they determined the optimal stress levels,the number of units measured at each test point,and the stress changingtime.The cost of testing is also an important factor that affects the testing design plan.Tang et al.[2]proposed an optimal design for SSADT and determined the sample size,testing duration and inspection times considering the testing cost.By using the Weiner process and the Gamma process respectively,Liao and Tseng[3]and Tseng[4]also proposed the optimal design for SSADT considering the testing cost.Li[5]also provided opti-mal solutions for SSADT considering competing failure causes.According to the competing failure rule,Li used the drift Brownian motion to establish a reliability model and minimized the asymptotic variance of the estimated 100th percentile of the competing reliability model under normal conditions with a constraint that the total experimental cost is below a pre-determined budget.Based on the analysis of the optimal plans with different budgets, stress levels and stress steps,Li[5]summarized the guidelines for stress loading principles of SSADT.

Typically,some information,e.g.,some laboratory testing data andeld operating data for similar products,is usually available prior to the experiments on a specic product.Therefore,Bayesian methods can play an important role.Chaloner and Verdinelli[6]and Clyde[7]reviewed the Bayesian experimental designs and indicated that it is difcult to obtain a posterior distribution in a closed form.There are two ways to solve this problem[7]. One is based on simulation and the other is based on the large-sample theory.

Research on Bayesian accelerated testing design mostly is based on accelerated life testing(ALT).Erkanli and Soyer[8]studied the Bayesian design for constant stress accelerated life testing(CSALT)using the Markov chain Monte Carlo(MCMC)method.To avoid computational issues,a curvetting approach was used to facilitate preposterior analysis andnd an optimal design.Zhang and Meeker[9]used large-sample approximation to obtain the Bayesian criterion.In this method,the general equivalence theorem(GET)was used tond out an optimal plan for this kind of non-linear problem.Liu and Tang proposed a scheme of sequential CSALT[10].In this scheme,testing under the highest stress isrst conducted to quickly acquire failures.Then,based on the failure data,prior distributions for lower stress levels are established using the Bayesian inference method.Theyrst came up with two Bayesian inferences,and then categorized them into all-at-one prior-distribution construction(APC)and full sequential prior-distribution construction(FSPC).Under their scheme,using large-sample approximation and failure informationcollectedunderthe highest stress level,the prior of lower stresses is obtained.By choosing the optimality criterion as minimizing the pre-posterior expectation of the asymptotic posterior variance at a percentile of interest under the normal stress level,the testing plan can be optimized.In other words,the remaining sample size and testing duration on each stress level can be specied.

There is limited published literature on Bayesian research for the ADT plan.Hamada et al.[11]used a mixed effect model with normal and inverse Gamma distributions as the priors for the parameters and proposed the optimal design for degradation testing.In this optimization,the objective was to minimize the total number of inspections,and the constraint was that the length of the credible interval should not exceed a given value.Liu and Tang[12]presenteda BayesianoptimaldesignforCSADT using quadratic loss as the optimality criterion,and used simulation combined with surfacetting as the stochastic optimizationmethod.Theircomparisonshowedthatthe Bayesiandesignapproachcouldsignicantlyhelpwith enhancementofrobustnessofanADT planagainsttheuncertainty[13].Shi and Meeker[14]studied the Bayesian optimal design for accelerated destructive degradation testing in which the estimation precision of a failure time distribution quantile under usage conditions was the optimal objective.They also used the nonlinear regression model to describe the degradation process and the simplied posterior distribution was obtained by a large-sample approximation.

From the above introduction,it could be known that the twoexistedADTBayesiandesignsfocusonconstantstress loading.And in[13],the objective is quadratic loss of special parameters in the accelerated model which might not be a good measure for the optimality of the testing plan. With regard to[14],the large-sample approximation was used to derive the simplied posterior distribution of parameters,and that means the sample size is large.But Chaloner and Verdinelli[6]have pointed out that when the sample size is large,the posterior distribution will be driven by the data and will not be sensitive to the prior distribution.Consequently,Bayesian design has little impact on the testing plan.Therefore,we investigate a new Bayesian optimal design for SSADT in which KL divergence will be as the optimality criterion to entirely measure the distance between prior and posterior distributions. Since KL divergence can be also known as measure of the information provided by testing,it is better than quadratic loss which only takes one aspect of testing into consideration.

The remaining paper is organized as follows.In Section 2,the frameworkof Bayesian optimal design for ADT is presented.In Section 3,drift Brownian motion and Arrheniusequationare used as the degradationmodeland the acceleration model,respectively,to illustrate the proposed procedures.In Section 4,KL divergenceorientedBayesian design and locally optimal design are both applied to battery’s SSADT.Finally,the conclusions are made and the future work is pointed out.

2.Framework of Bayesian optimal design for SSADT

The Bayesian testing plan is essentially a Bayesian decision problem.The objective of the experiment is to maximize the expected utility or minimize the expected loss.Since the testing plan needs to be designed before sample data collected,the expected utility should be integrated over possible outcomes in the sample space Ω.And considering the uncertainty of parameter vector θ,the utility also needs to be the expectation in the parameter space Θ. Therefore,for any design η,the expected utility function Λ(η)of the best decision[6]is expressed as

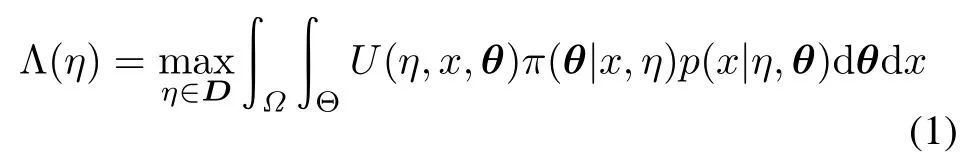
where π(θ)is the prior distribution of parameter θ; π(θ|x,η)is the posterior distribution under the design η, data x and prior π(θ);U(η,x,θ)is the utility function which depends on the data x of a future experiment with designη andparametervectorθ;p(x|η,θ)is thelikelihood function with the condition of design η and parameter vector θ.

2.1Surface ftting based Bayesian optimal design for SSADT

The basic optimization steps using surfacetting are presented below and aow chart is shown in Fig.1.

Fig.1 Flow chart of basic steps for SSADT Bayesian design based on surface ftting

When the sample size is given and the measurement interval is constant in SSADT,the magnitudes of stress levels and the number of measurements need to be optimized,i.e.these two factors are decision variables which span the decision space of the testing design.In order to reduce the computation time,it is necessary to reparameterize stress levels and measurement numbers.For klevel SSADT,S is a vector of the accelerated stress level, S=(s1,...,sl,...,sk),where the element slmeans the magnitude of the lth stress level.M is a measurement vector,M=(m1,...,ml,...,mk),where the element mlmeans there are mldegradation data collected on the lth stress level.Here,we normalize these two vectors,S and M.With regard to S,we introduce the stress ratio ξ=(ξ1,...,ξl,...,ξk)(ξl∈[0,1])to simplify the specied stress values:

Corresponding to M,the measurement allocation ratio ρ=(ρ1,...,ρl,...,ρk)(ρl∈(0,1))denotes the number of measurements assigned to the lth stress level:

In this way,our design space involves the stress ratio ξ and the allocation ratio ρ.For the case of two stress levels(also known as 2-point design),the highest stress level could bexed as smax,i.e.s2=smaxand ξ2=1,then only ξ1=(s1−smin)/(smax−smin)needs to be optimized.Similarly,we only need to determine ρ1,because of the given total measurements and ρ2=1−ρ1.

In addition,it is hard to specify the exact structure of the surface regression model.Therefore,a non-parametric method such as Kernel smoother is preferred.For comparison,both locally weighted polynomial(e.g.locally weighted scatterplot smoothing)and polynomial regression methods are used in this paper.

2.2KL divergence

Many researchers prefer to use asymptotical approximation as the optimization criterion.If asymptotical approximation is used for optimality,then historical information can play a little role in parameter estimations.On the other hand,asymptotical approximationis reasonableonly when thesamplesizeislarge,butthisrequirementishardtomeet in real world.

In the Bayesian theory,KL divergence is always used as a measure of distance between a prior distribution and a posterior distribution.From the perspective of Shannon information,it also represents the information gain contributed by an experiment,also known as relative entropy. Based on this fact,to the process of designing the optimalSSADT with respect to maximizing KL divergence is presented in this paper.

Accordingto Lindley[16],the informationcontained in the prior distribution is

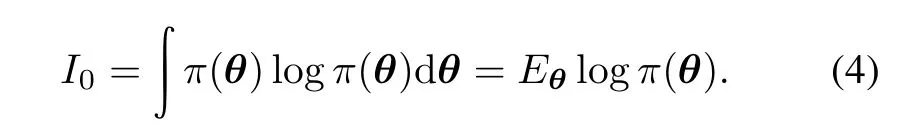
The amount of information taken with posterior distribution is expressed as

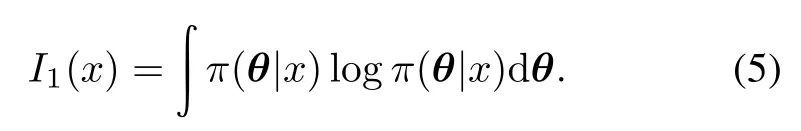
The information provided by experiment η was dened by Lindley[16]as follows:

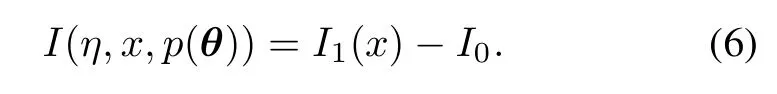
Based on the Bayesian theorem,the expectation of experimental information can be written as

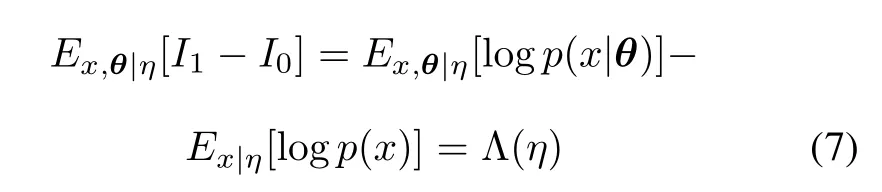
where p(x)is the marginal likelihood and also a normalizing constant expressed as

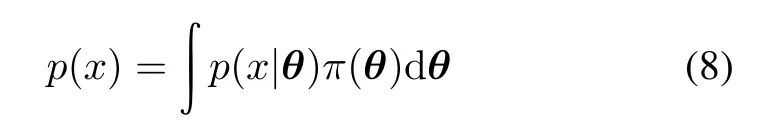
Equation(7)is known as KL divergenceand it is the expected utility of our Bayesian optimal design for SSADT. For most of the posterior distributions,it is hard to get a closed form analytical solution.In this situation,the best choice to compute KL divergence is the Monte Carlo method.

Since p(x|θ)is the likelihood function,it is relatively easy to calculate Ex,θ|η[logp(x|θ)]using Monte Carlo simulation.However,the marginal likelihood function p(x)presents a signicant challenge,which is a topic of ongoing research.The MCMC sampling method is one of thesolutionsto solvethis problemandcanbeimplemented using a software called WinBUGS[17,18].The following Laplace-Metropolis algorithm will be used to estimate the marginallikelihoodEx|η[logp(x)],basedonguidanceprovided by Ntzoufras[18].

Since KL divergence represents the information gained fromthe experiments,theoptimalproblemofBayesian design for SSADT could be

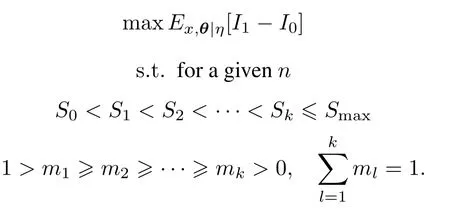
The steps for KL divergencebased on surfacetting are shown as below:

Step 1Divide design space D=ξ1×ρ1into equal segments in the direction of the stress ratio ξ1and the allocation ratio ρ1.Then,there will be RDsimulating points in the design space with boundaries.

Step 2Draw the design ηr(r=1,...,RD)from D, and simulate parameter θrfrom their corresponding prior distributions.Based on the simulated θr,generate degradation data xrqfrom sampling distribution pdf(x|θrh)for R1times(q=1,...,R1).Then use the MCMC algorithm to estimate the posterior means¯θqand Σqfor the qth simulated xrq.

Step 3Calculate the marginal likelihood p(xrq)using

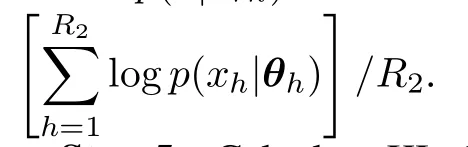
Step 5Calculate KL divergence Urbased on(7)for the design ηr.

Step 6Go to Step 1 and repeat Steps 1–5 for every feasible design in the design space.

Step 7Based on the pair(ηr,Ur),the surface can betted.

Step 8The optimal plan for SSADT is obtained by taking the maximum of this surface.

3.Illustration

In this section,we will narrow down to a specic degradation model and an acceleration model based on some assumptions.Then,the process of optimal design will be discussed.

3.1Assumptions and models

3.1.1 Assumptions

Brownian motion is one of the most powerful stochastic processes in continuous time and space.It has wide applications in many disciplines such as physics,economics, communication theory,and reliability theory.Therefore, it is used herein tot the accelerated degradation process [19].

The following assumptions are made in the analysis [3,20]:

Assumption 1Degradation is irreversible.

Assumption 2Degradation mechanism will not change with stress.

Assumption 3Under the normal condition S0and klevel accelerated conditions,s1＜s2＜···＜sk,performance degradation process Ylfollows the drift Brownian motion(DBM)with drift d(sl)＞0 and dispersion σl＞0 (l=1,...,k):

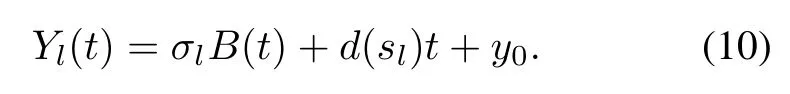
Assumption 4Dispersion parameter σldoes not change with stress,i.e.σ0=σ1=···=σk=σ.

Assumption 5The drift parameter can be called as the degradation rate and regarded as the function of stress conditions,i.e.the drift parameteris an accelerationmodel

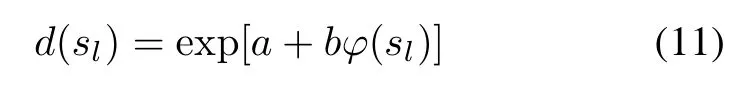
where slis the accelerated variable and ϕ(sl)is the function of sl,e.g.ϕ(s)=1/T,when the accelerated variable is absolute temperature T.

Assumption 6The prior distributions for parameters a,b and 1/σ2are independent of each other,where y0=0 and the unknown parameter vector θ={a,b,υ},υ= 1/σ2.

3.1.2 Likelihood function

Let Δt be the non-overlapped interval of performance inspection,then the test time on the lth stress level is tland tl=mlΔt,and the total test time is t and t=mΔt.

Meanwhile,tiljis the time of the jth inspection of the ith item on the lth stress level(i=1,...,n;l= 1,...,k;j=1,...,ml),and the corresponding inspection result is yilj.

The Brownian motion is a Gaussian process,so the increment x over non-overlappedinterval Δt is independent and normally distributed with mean d(s)Δt and variance σ2Δt.The probability density function of the independent increment can be expressed as

Accordingtothecumulativeexposuremodel,thatis,the remaining life of test items depends only on the current cumulative damage and current stress,the likelihood function of SSADT for all degradationincrements of n items is given by

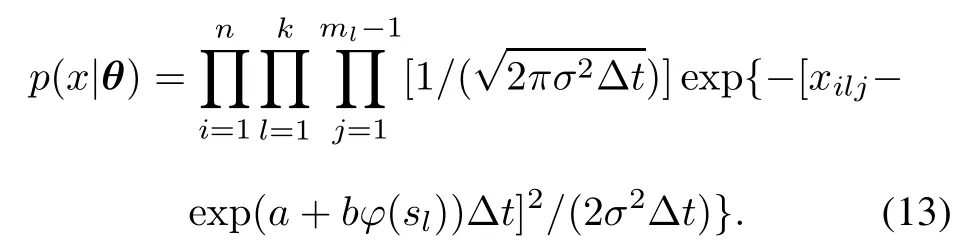
Its log-likelihood function is

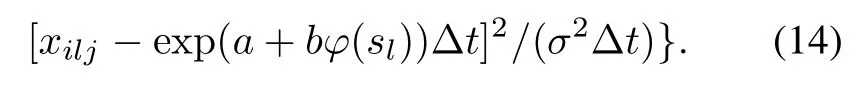
3.1.3 Bayesian model for SSADT

Let π(a),π(b)and π(υ)be the prior distributions of parametersa,b and υ,respectively,then their posteriordistributions could be obtained based on the Bayesian theorem as

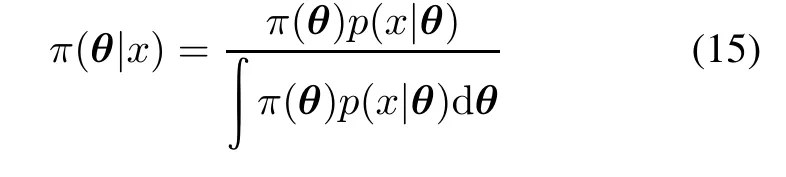
3.2Example for Bayesian design of SSADT

Based on the above framework,assumptions and models,a numerical example is presented herein to illustrate the Bayesian planning of the SSADT procedure.In this example,the acceleration model is based on the Arrhenius equation,ϕ(s)=1/T.

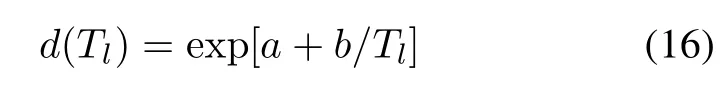
where b= −Ea/k,k is Boltzmann’s constant,k= 8.617 1×10−5eV/K and Eais the activation energy with unit eV.

According to the increment x∼N(d(s)Δt,σ2Δt)and the conjugate prior distribution theory,it is known that parametersa andbindependentlyfollownormaldistributionswith means μa,μband variances σa,σb,respectively,and υ follows Gamma distribution with scale α and shape β, i.e.a∼N(μa,σa),b∼N(μb,σb)and v∼Γ(α,β).In order to derive an optimal plan,the hyper-parameters are needed and are summarized in Table 1.

Table 1 Settings of the numerical example

3.2.1 KL divergence oriented optimal design

With the above settings,the specied optimal problem for Bayesian design of SSADT is

Afterdividingthedesignspaceintonineequalsegments in the direction of the stress ratio and the allocation ratio,there will be RD=100 different candidate plans in the design space D,including boundaries.The surfacetting algorithms are quadratic polynomial based on locally weighted quadratic regression.Let R1=40 and R2=80, then the smoothed results are shown in Fig.2 following the steps mentioned in Section 2.2.Locally weighted scatterplot smoother(LOWESS)in Matlab is used to realize locally weighted quadratic regression in Fig.2.

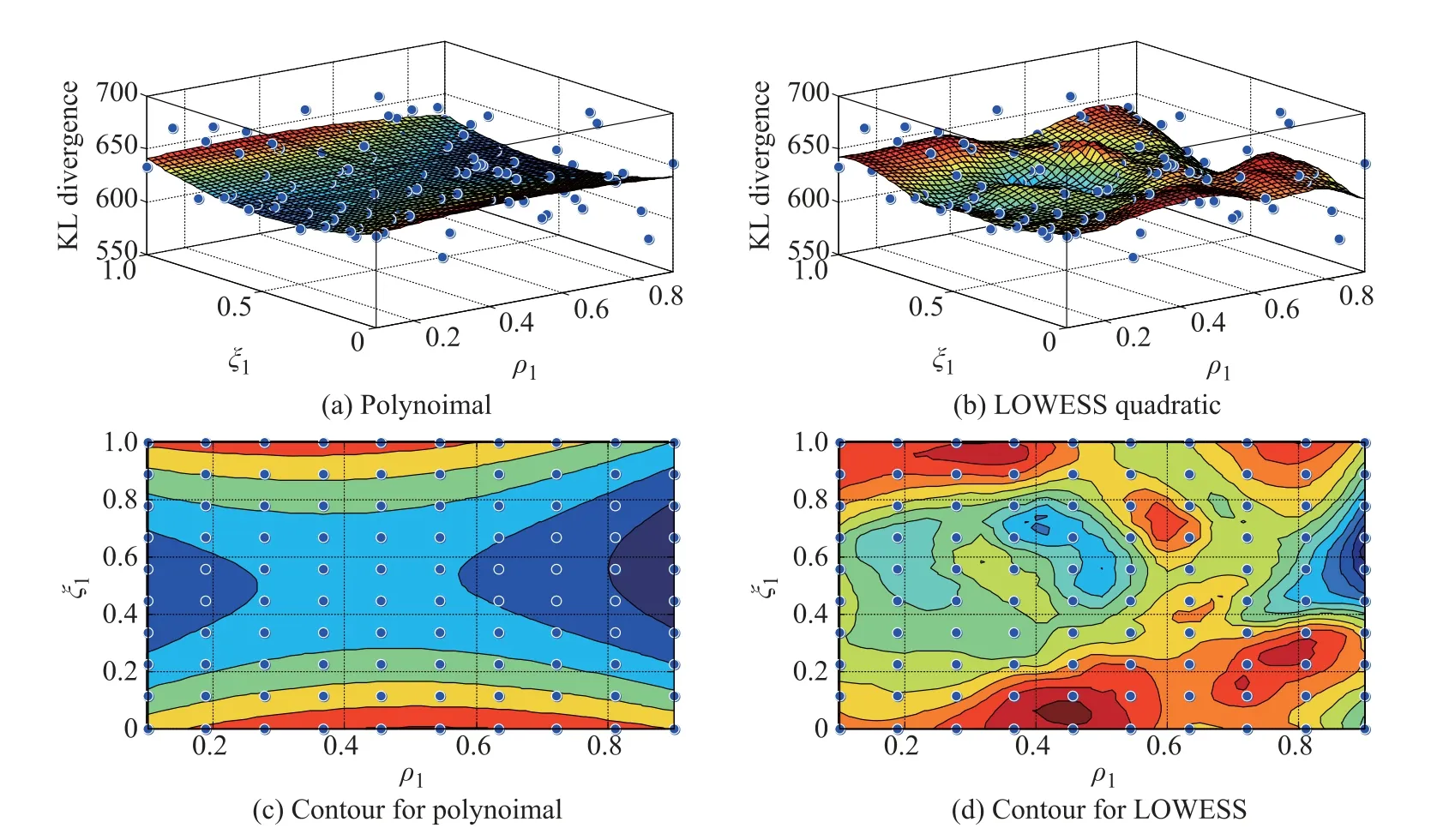
Fig.2 Two-point optimal design(KL divergence oriented)

From Fig.2,the appropriate plan is around(ξ1,ρ1)= (0.05,0.45),and the optimal plan is shown in Table 2.

Table 2 Optimal plan using KL divergence as optimal criteria

3.2.2 Quadratic loss oriented optimal design

Similar to KL divergence,another typical quadratic function is quadratic loss[21].Quadratic loss is popular because of its straightforward computation and similarity to the classical least square method.The quadratic loss function can be written as

where,‖·‖is the Euclidean norm.

Therelationshipbetweentheexpectedutilityandthe expected loss function is

Similar to KL divergence,steps for optimal design involve dividing design space,drawing design η,generating degradationdata,andestimatingthequadraticlossL.Aftertting surface of pair(η,L),the optimal plan for SSADT is obtained by taking the minimum of the surface.

Let R1=40,the optimal design results for the case of quadratic loss as the objective are presented below.In this example,surfacetting algorithms of quadratic polynomial and locally weighted quadratic regression are both utilized and the results are shown in Fig.3,respectively.

Fig.3 Two-point optimal design with smoothing outliers(n=3)

In the case of KL divergence,the difculty of choosing an appropriate solution according to the importance of parameters can be avoided,while tradeoff should be considered when quadratic loss is considered as the optimal criterion.The results indicate that the KL divergence method is a better choice than the quadratic loss method for optimal design.

Table 3 Optimal plans using quadratic loss as optimal criteria

4.Validation and application

Recently,rechargeablebatteries have becomecritical com-ponents in various applications,ranging from laptops to electric vehicles,as well as the key sub-system component of smart grids for energy storage.High performance batteries that have long life and high reliability are used in various applications.In order to quickly and efciently predict the battery’s remaining useful life(RUL),a cost-effective and time-saving testing plan should be designed.This can be accomplished using ADT.In this section,the proposed method will be applied to optimize the testing plan for Liion battery by using NASA battery data[23]as historical information.

4.1Prior distributions of batteries

There are 24 batteries degradation data from NASA.To have similar discharging proles and temperature conditions,batteries B0005,B0006,B0007 and B0018 are selected and the parameterpriors are determined.The details of these four batteries are shown in Table 4 and degradations of the capacity are shown in Fig.4.

Table 4 Testing details of four batteries

Fig.4 Capacity degradation

In practice,the discharging capacity is more important than the charging capacity.Therefore,the discharging capacity is considered in determining the priors of parameters.The assumptions and models presented in Section 3.1 are followed in this analysis.

Generally,the battery’s discharging capacity decreases with time.However,to meet the requirement of DBM wherethedriftshouldbegreaterthan0,thecapacitydegradation is converted to depict how much degradation has occurred.For example,there is no degradation at the startingpoint,but degradationaccumulateswith time.The converted and normalized capacity are shown in Fig.5.

Fig.5 Capacity converted degradation

With regard to simplicity and validity,a linear model p1t+p2,is chosen to describe the capacity degradation trend with time.The estimations of p1and p2for each battery are shown in Table 5.

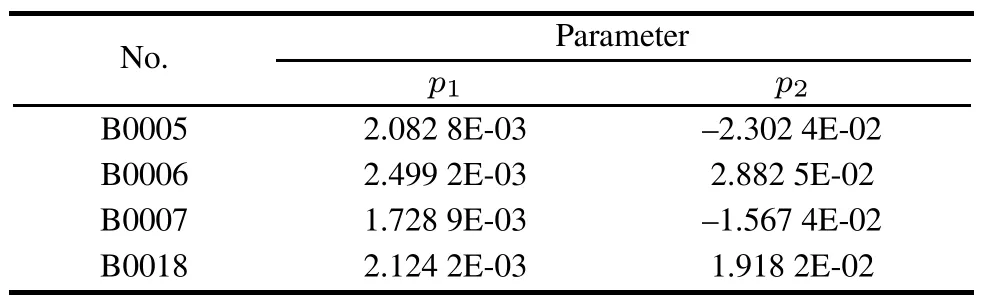
Table 5 Coeffcients of linear model

Using the assumptions in Section 3.1,the expectation of DBM is E(Y(t))=d(s)t+y0.Therefore,p1= d(s)=exp(a+b/T)=exp(a−Ea/kT),b=−Ea/kT, p2=y0.For lithium-ion battery,it is appropriate that the mean of Eais assumed as 0.5 eV.Consequently,the mean of the parameter b can be–5 802.Based on engineering judgment,its variance can be assumed as 10, then b∼ N(−5 802,10).In order to specify the prior of the parameter a,the mean of the parameter a is determined as a=13.365 5 based on the average of degradation rate p1and Ea=0.5 eV.The parameter a ranges from 13.166 9 to 13.535 4,which corresponds to the maximum and minimum of the degradation rate p1,respectively.Assuming a follows a normal distribution,based on the 3-sigma rule,the variance of a is around 0.06 and then a∼N(13.365 5,0.06).The prior of the parameter σ2is assumed as 1/σ2∼Γ(1.3,1).

4.2Bayesian and locally optimal design for batteries

4.2.1 Bayesian optimal design

Based on the analysis in Section 3,KL divergence is used as the optimal objective.Table 6 summarizes the details on the Bayesian optimal design of the battery.

Table 6 Bayesian optimal design details of batteries

Smoothed results based on polynomial and LOWESS surfacetting algorithmswith two differentcases in which R1equals 20 and 40 times are shown in Fig.6,respectively.These results indicate that:

(i)The outliers caused by simulation indicate that the results are unstable and optimal designs from these two different cases are not consistent.

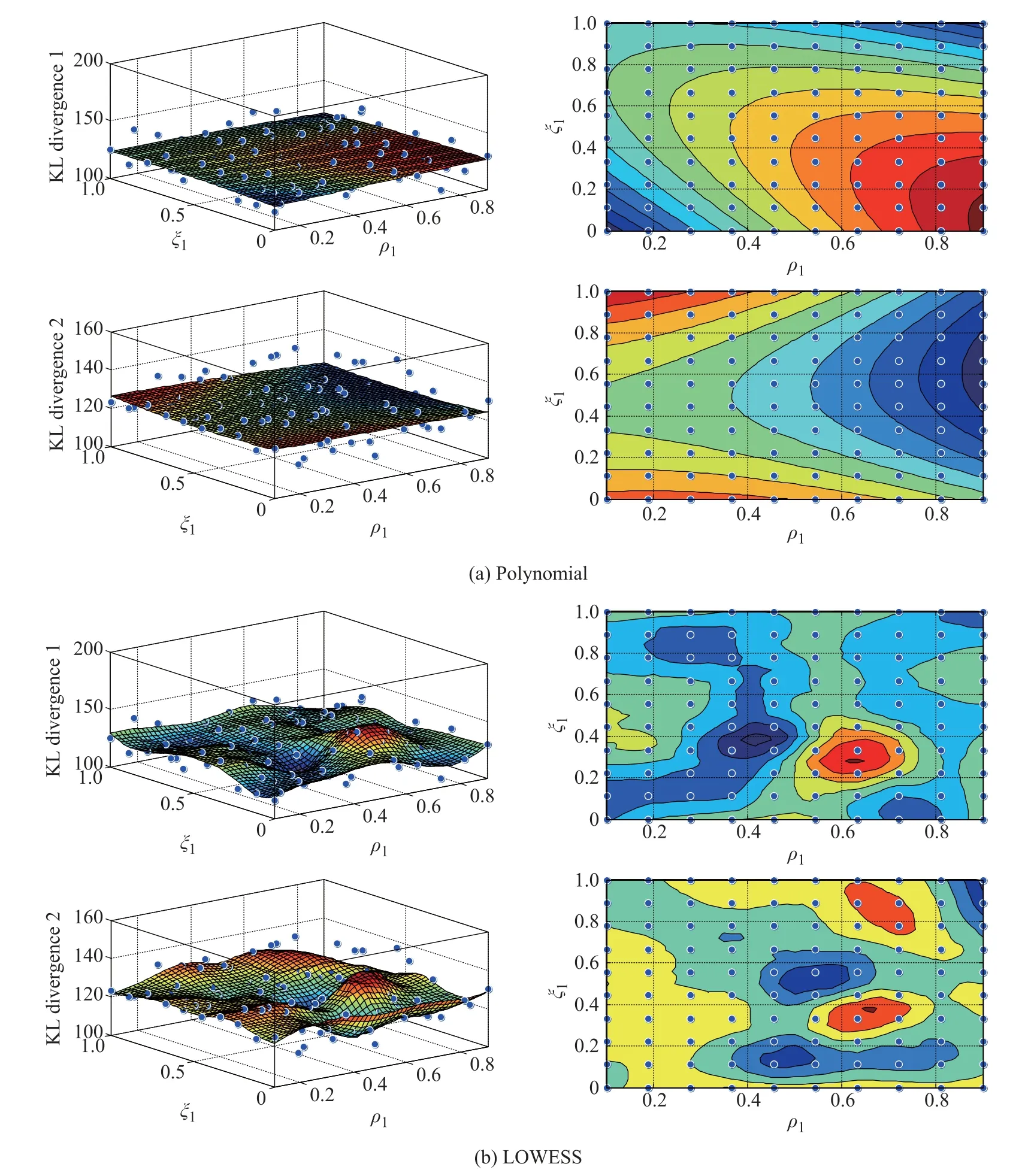
Fig.6 Two-point optimal design for batteries

(ii)Whenthepolynomialmethodis usedtot theresults fromthe two differentcases,a completelyoppositesurface trendis observed(seeFig.6(a)).Therefore,the polynomial (quadratic in this case)based surfacetting cannot satisfy the relationship between the KL divergence and the two independent variables,stress and measurement.

(iii)When the LOWESS method is used tot the results,the optimal solutions are almost in the same area(see Fig.6(b)).The appropriate solution is around (ξ1,ρ1)=(0.3,0.65).Therefore,it can be concluded that the LOWESS method is a better choice for the optimal design of SSADT.

According to the analysis above,i.e.s1is 0.3 and m1is 0.65,the optimal plan is shown in Table 7.

Table 7 Optimal plan for SSADT using Bayesian optimal design

4.2.2 Locally optimal design for batteries

Similar to KL divergence,D-optimality based on information is used as the optimal objective in locally optimal design(non-Bayesiandesign).It is importantto minimizethe estimation uncertainty of model parameters,i.e.to minimize the variance of model parameters,and at the same time maximize the determinant of the Fisher informationmatrix,as the information matrix has a reciprocal relationship with the variance-covariance matrix.Hence,the objective function for D-optimality in this case is as follows [24]:

where F(θ)is the Fisher information matrix,and its element Fij=E[−(∂2logp(x|θ,η))/(∂θi∂θj)].According to the priors of the acceleration model parameters,a and b are set as the means of their distributions.That is (a,b)=(13.655,−5 802.5).The dispersion parameter σ is set based on the variance of the observed accelerated degradation data,σ=0.151 7.

The details of this locally optimal design are shown as follows:

(i)The number of units is three,and the total number of measurements are 100;

(ii)The temperature range ranges from 30°C to 50°C, s2=50°C,and 30°C≤s1＜s2;

(iii)Measurement m1ranges from 10 to 90,m2= 100−m1;

(iv)Design space S×M=[30,50]×[10,90],s1and m1are integers;

(v)For every design η in the space,calculate the determinant of the Fisher information matrix|F(θ)|;

(vi)The optimal plan for SSADT is obtained by taking the maximum of|F(θ)|.

The results are shown in Fig.7.

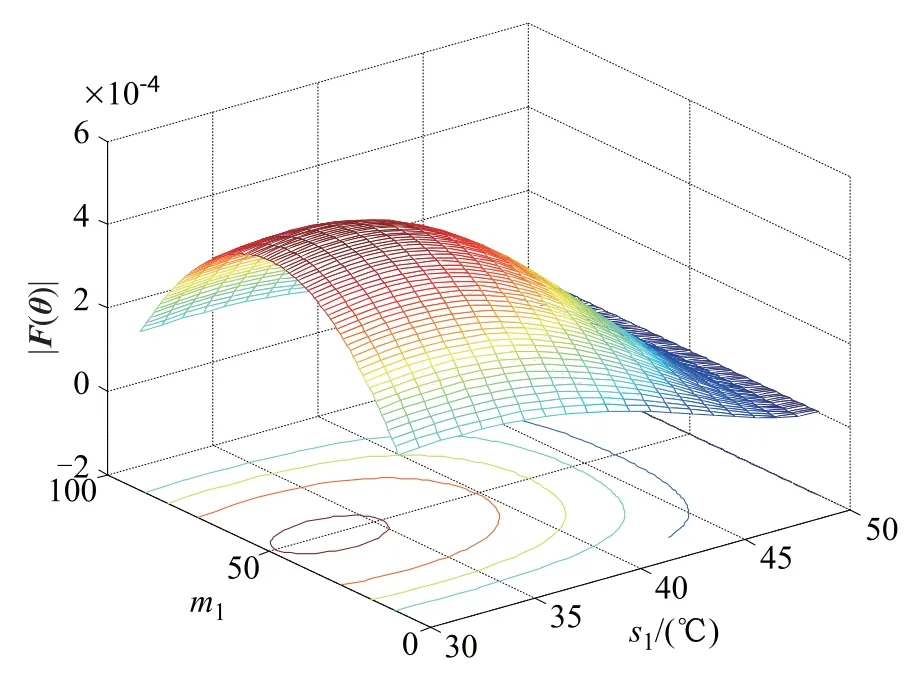
Fig.7 Two-point locally optimal design

The optimal solution is shown in Table 8.

Table 8 Optimal plan for SSADT using locally optimal design

4.3Comparison

From Table 7 and Table 8,it can be seen that the Bayesian optimal plan and the local one are similar to each other. From a stress level point of view,there is no signicant differencebetweenthe localoptimizationandtheBayesian optimization,because the temperature range of the former is[33,50]and the latter is[36,50](both in°C).However,the 3°C is insignicant in real world.With low stress levels and slow degradation rates,more performance measurements should be assigned at lower stress levels.Therefore,it is concluded that the results in Table 7 are more reasonable.

According to Chaloner and Verdinelli[6],the differences between the Bayesian design and the non-Bayesian design are of less importance if the sample size n is large. When n is large,the posterior distribution will be driven by the data and will not be sensitive to the prior distribution.On the contrary,when n is small,the prior distribution will have more inuence on the posterior distribution and the testing plan.For the battery case study presented in this paper,the sample size is three,so Bayesian design is a better choice.

5.Conclusions

Inthis paper,aBayesiandesignframeworkforADTis proposed,in which information based KL divergence is used as the optimal objective.The following conclusions can be drawn from this study:

(i)Numerical analysis results show that KL divergence oriented optimization can provide a more reasonable testing plan because it can comprehensively depict utilities contributed by experiments,while quadratic loss can only focus on one aspect.

(iii)The battery application presented in this study validates that the proposed method is more efcient and practical than local optimization.

This paper provides details about how to optimize stress levels and measurements for SSADT with only two stress levels.In practice,the number of stress levels may vary anywhere between three tove levels and additional research is warranted to validate the proposed approach for over two stress levels.The testing cost is a signicant constraining factor which cannot be neglected.It is also important that the choice and sensitivity analysis of prior distribution should be conducted in the Bayesian design and interference.In future,the proposed method should be extended to those applications.

[1]S.J.Park,B.J.Yum,S.Balamurali.Optimal design of stepstress degradation tests in the case of destructive measurement. Quality Technology&Quantitative Management,2004,1(1):105–124.

[2]L.C.Tang,G.Yang,M.Xie.Planning of step-stress accelerated degradation test.Proc.of the Reliability and Maintainability Symposium,2004:287–292.

[3]C.M.Liao,S.T.Tseng.Optimal design for step-stress accelerated degradation tests.IEEE Trans.on Reliability,2006,55(1): 59–66.

[4]S.T.Tseng,N.Balakrishnan,C.C.Tsai.Optimal step-stress accelerated degradation test plan for gamma degradation processes. IEEE Trans.on Reliability,2009,58(4):611–618.

[5]X.Li,T.Jiang.Optimal design for step-stress accelerated degradation testing with competing failure modes.Proc.of the Reliability and Maintainability Symposium,2009:64–68.

[6]K.Chaloner,I.Verdinelli.Bayesian experimental design:a review.Statistical Science,1995,10(3):273–304.

[7]N.J.Smelser,P.B.Baltes.International encyclopedia of the social&behavioral sciences.Oxford:Pergamon,2001.

[8]A.Erkanli,R.Soyer.Simulation-based designs for accelerated life tests.Journal of Statistical Planning and Inference,2000, 90(2):335–348.

[9]Y.Zhang,W.Q.Meeker.Bayesian methods for planning accelerated life tests.Technometrics,2006,48(1):49–60.

[10]X.Liu,L.C.Tang.Asequential constant-stress accelerated life testing scheme and its Bayesian inference.Quality and Reliability Engineering International,2009,25(1):91–109.

[11]M.S.Hamada,A.Wilson,C.S.Reese,et al.Bayesian reliability.New York:Springer,2008.

[12]X.Liu,L.C.Tang.A Bayesian optimal design for accelerated degradation tests.Qualityand ReliabilityEngineering International,2010,26(8):863–875.

[13]Y.Shi,W.Q.Meeker.Bayesian methods for accelerated destructive degradation test planning.IEEE Trans.on Reliability, 2012,61(1):245–253.

[14]Y.Shi,W.Q.Meeker.Bayesian methods for accelerated destructive degradation test planning.IEEE Trans.on Reliability,2012,61(1):245–253.

[15]P.Mller,G.Parmigiani.Optimal design via curvetting of Monte Carlo experiments.Journal of the American Statistical Association,1995,90(432):1322–1330.

[16]D.V.Lindley.On a measure of the information provided by an experiment.The Annals of Mathematical Statistics,1956, 986–1005.

[17]D.J.Lunn,A.Thomas,N.Best,et al.WinBUGS-a Bayesian modelling framework:concepts,structure,and extensibility. Statistics and Computing,2000,10(4):325–337.

[18]I.Ntzoufras.Bayesian modeling using WinBUGS.Hoboken: John Wiley&Sons,2011.

[19]H.T.Liao,E.A.Elsayed.Reliability inference foreld conditions from accelerated degradation testing.Naval Research Logistics,2006,53(6):576–587.

[20]H.Lim,B.J.Yum.Optimal design of accelerated degradation tests based on Wiener process models.Journal of Applied Statistics,2011,38(2):309–325.

[21]C.P.Robert.The Bayesian choice:from decision-theoretic foundations to computational implementation.New York: Springer,2007.

[22]X.Li,T.Jiang,F.Sun.Constant stress ADT for superluminescent diode and parameter sensitivity analysis.Eksploatacja I Niezawodnosc-Maintenance And Reliability,2010,46(2):21–26.

[23]B.Saha,K.Goebel.Batterydataset.http://ti.arc.nasa.gov/tech/ dash/pcoe/prognostic-data-repository/.

[24]Z.Ge,T.Jiang,S.Han,et al.Design of accelerated degradation testing with multiple stresses based on D optimality.Systems Engineering and Electronics,2012,34(4):846–853.(in Chinese)

Biographies

Xiaoyang Li received her B.S.degree from Beihang University(BUAA)in quality and reliability,in 2002 and Ph.D.degree from BUAA in systems engineering of aeronautics and astronautics, in 2007.She is an associated professor in the Science and Technology on Reliability and Environmental Engineering Laboratory,BUAA,where she has been afliated since 2007.She hasbeen to NSF Industry/University Cooperative Research Center on Intelligent Maintenance Systems(IMS),University of Cincinnati,as a visiting professor for one year.Her research interests focus on life prediction,design of experiment,and accelerated testing.

E-mail:leexy@buaa.edu.cn

Mohammad Rezvanizaniani received his B.S.degree from Iran Science and Technology University, Tehran,Iran,in mechanical engineering,in 2002 and M.S.degree from Lule˚a University of Technology,Lule˚a,Sweden,in maintenance management and engineering,in 2008.He is a Ph.D.student in IMS.He has the deep knowledge in theeld of smart battery,electric vehicle,applying prognostics &health management tools,reliability analysis and preventive maintenance.

E-mail:rezvansd@mail.uc.edu

Zhengzheng Ge received her B.S.degree and Ph.D. degree in automation in 2006 and 2012 respectively from Hebei University of Technology.She is now a senior engineer in Beijing Institute of Electronic System Engineering.Her recent work is on optimal design for accelerated degradation testing.Her research interests include reliability testing,accelerated test modeling and test designing.

E-mail:gezhengzheng1983@163.com

Mohamed Abuali received his B.S.degree in systems engineering from University of Arizona in 2003,M.S.degree in industrial engineering from The American University in Cairo in 2005,and Ph.D.degree in industrial engineering from the Center for Intelligent Maintenance Systems(IMS)at the University ofCincinnati in 2010.He isnow the CEO of FORCAM and responsible for leading and growing FORCAM operations in the Americas.He is also a project management professional (PMP),a six sigma green belt(SSGB)and a certied quality engineer (CQE).

E-mail:abualima@mail.uc.edu

Jay Lee is an Ohio Eminent Scholar and L.W.Scott Alter Chair Professor at the University of Cincinnati and is the founding director of National Science Foundation(NSF)Industry/University Cooperative Research Center(I/UCRC)on Intelligent Maintenance Systems.His current research focuses on dominant innovation design tools and smart infotronics technologies forservice andmaintenance automation applications.

E-mail:jay.lee@uc.edu

10.1109/JSEE.2015.00058

Manuscript received April 09,2014.

*Corresponding author.

This work was supported by the National Natural Science Foundation of China(61104182).