Opportunistic maintenance for multi-component systems considering structural dependence and economic dependence

Junbao Geng,Michael Azarian,and Michael Pecht

1.College of Power Engineering,Naval University of Engineering,Wuhan 430033,China;

2.Center for Advanced Life Cycle Engineering,University of Maryland,College Park 20742,USA

Opportunistic maintenance for multi-component systems considering structural dependence and economic dependence

Junbao Geng1,*,Michael Azarian2,and Michael Pecht2

1.College of Power Engineering,Naval University of Engineering,Wuhan 430033,China;

2.Center for Advanced Life Cycle Engineering,University of Maryland,College Park 20742,USA

Although opportunistic maintenance strategies are widely used for multi-component systems,all opportunistic maintenance strategies only consider economic dependence and do not take structural dependence into account.An opportunistic maintenance strategy is presented for a multi-component system that considers both structural dependence and economic dependence. The cost relation and time relation among components based on structural dependence are developed.The maintenance strategy for each component of a multi-component system involves one ofve maintenance actions,namely,no-maintenance,a minimal maintenance action,an imperfect maintenance action,a perfect maintenance action,and a replacement action.The maintenance action is determined by the virtual age of the component,the life expectancy of the component,and the age threshold values. Monte Carlo simulation is designed to obtain the optimal opportunistic maintenance strategy of the system over its lifetime.The simulation result reveals that the minimum maintenance cost with a strategy that considers structural dependence is less than that with a strategy that does not consider structural dependence.The availability with a strategy that considers structural dependence is greater than that with a strategy that does not consider structural dependence under the same conditions.

opportunistic maintenance,multi-component system, structural dependence,Monte Carlo simulation,maintenance cost.

1.Introduction

Maintenance strategies can be classied as corrective maintenance,preventive maintenance,opportunistic maintenance,condition-based maintenance,and predictive maintenance[1].Opportunistic maintenance comprises a set of maintenance activities that are performed on a component when an opportunityexists during the performance of maintenance activities on other components in a multicomponent system.Because of the dependencies among the components in a multi-component system,opportunistic maintenance can be used to obtain an optimal maintenance strategy.

Three types of interactions among the components of a multi-component system exist:economic dependence, structuraldependence,andstochasticdependence[2].Economicdependencemeansthat the costs of replacementand maintenance are different when applying different maintenance strategies for a multi-component system.Structural dependence means that other components have to be disassembled or taken apart in order to maintain a particular component.Although maintenance strategies are widely used for multi-component systems in the existing literature,all opportunistic maintenance strategies are based on economic dependence.However,structural dependence among the components greatly impacts the maintenance cost and maintenance time for a multi-component system withstrongstructuraldependence.Ifstructuraldependence is not considered,an opportunistic maintenance strategy willnotbeanoptimalstrategy.Inthispaper,anopportunisticmaintenancestrategyforamulti-componentsystemthat considersbothstructuraldependenceandeconomicdependence is presented.

The rest of this paper is organizedas follows.In Section 2,a literature review of opportunistic maintenance is presented.Section 3 develops an opportunistic maintenance strategy for a multi-component system that considers both structural dependence and economic dependence.Section 4introducesa MonteCarlo simulationprocessanddemonstrates it in an example.Conclusions are provided in Section 5.

2.Literature review

Opportunistic maintenance wasrst studied by Radner and Jorgenson[3]and McCall[4].Since then,opportunistic maintenance strategies have been improved.The mod-eling methodology adopted in opportunistic maintenance strategies can be classied into two approaches:analytical and simulation[5].In the analytical approach,the objective function is expressed in an analytical form with parameters.Many methods have been employed to develop opportunistic maintenance models,such as dynamic semi-Markov programming[6,7],renewal theory[8],coupling method[9],Gamma process[10],universal generating function[11],fuzzy theory[12],the maximum likelihood estimation[13].These analytical approaches become highly complex as the number of components increases. The simulation approach is one way to solve this complex problem.Using the simulation approach,a system with many components can be modeled with relative ease. TheMonteCarlosimulationmethodcanbeusedtoachieve an optimal solution for a complex system.Simulation has been used to obtain the optimal opportunistic maintenance strategies in many studies[14–20].

Summing up the existing literature,there are four kinds of methodsto obtain an optimalopportunisticmaintenance strategy.Therst method is for the maintenance cost to be minimized without other constraints,such as availability and reliability.For example,the optimal strategy is that the maintenance cost is the lowest,which does not consider the values of other performance[5,6,21–23].The second method is for the maintenance cost to be minimized with some constraints,such as availability and reliability.For example,a maintenance strategy has been made to achieve the minimum maintenance cost within the constraints of time and system availability requirements[24,25].The thirdmethodisforthesystemavailabilitytobemaximized, while the cost is less than some predetermined value.For example,a simulation algorithm based on an opportunistic maintenance strategy has been designed to maximize the total availability[15].The fourth method is for the life cycle cost to be minimized with some constraints[26].For example,the impact of opportunistic maintenance on the life cycle cost of a reciprocating compressor has been simulated.The simulation results showed that the life cycle cost of a reciprocatingcompressor was greatly reduced after opportunistic maintenance,and the operational availability was within the predetermined range[19].For any specic case,one of the abovefour methods can be chosen to obtain an optimal maintenance strategy.

Several factors should be considered in making an opportunistic maintenance strategy,including the maintenance action classication,effect of the maintenance action,maintenance cost breakdown structure,and choice of maintenance action.There are different maintenance action classications in the existing literature.For example, Pham and Wang classied the maintenance actions as minimal repair,imperfect preventive maintenance,and perfect preventive maintenance[27].Wang and Pham classied the maintenance actions as imperfect repair,imperfect preventive maintenance,and perfect preventive maintenance[28].Ding and Tian[16]classied preventive maintenanceinto perfect,imperfect,and two-level actions. Tambe et al.[24]classied opportunistic maintenance actions into replacementaction,repair action,andno maintenanceaction.Thesedifferencesinmaintenanceactionclassicationswill causediversityinthechoiceofmaintenance action in an opportunistic maintenance strategy.The effect of maintenanceaction is used to estimate the age of a component after one maintenance action.The restoration factor has been used to describe the effect of one maintenance action on a component[16,19,24].The maintenance cost breakdown structure has a signicant impact on the accuracy of the maintenance cost estimate.If a maintenance costelementis omitted,thenthe maintenancecost estimate is not accurate.Thus,a detailed maintenance cost breakdown structure should be established to obtain an accurate cost estimate.Tambe et al.stated that the maintenancecost breakdown structure consisted of the replacement cost,repair cost,downtime cost,residual cost,and failure cost [24].Hu et al.considered that the cost breakdown structure comprised the repair cost,set-up cost,and production loss[17].The above cost breakdown structures are not detailed enough,so a more detailed cost breakdown structure should be established that combines the results from the existing literature.The choice of maintenance action is used to determine which component should undergo.Differentmaintenanceactionchoices havebeenproposed.For example,maintenance action choices based on age or time are commonly used[18,19].The reliability or failure rate can also be used to determine the choice of the opportunistic maintenance[29,30].The maintenance action choice based on age or time is more popular than that based on the reliability or failure rate.

Neither analytical approaches nor simulation approaches to opportunistic maintenance include structural dependence.None of the optimization methods considers structural dependence.Structural dependence is not considered to be a factor in making an opportunistic maintenance strategy.In particular,none of the cost breakdown structures includes the cost caused by structural dependence.However,structural dependence among components impacts both the maintenance cost and the availability of a multi-component system.Thus,an opportunistic maintenance strategy will not be an optimal strategy if the structural dependenceamong componentsis not considered in an opportunistic maintenance strategy.

3.Opportunistic maintenance strategy

This section develops the details of models and methodsused in an opportunistic maintenance strategy for a multicomponent system considering structural dependence and economic dependence.

3.1Structural dependence

There are three possible structural dependencies between component A and component B.One is that there is no structural dependence;that is,the components do not affect each other.The second dependence is single dependence.For example,component A is restricted by component B,but component B is not restricted by component A.The third dependence is a relation where both components are restricted by each other:component A is restricted by componentB,and component B is restricted by component A.

Suppose that the components are marked by an integer,e.g.,i is denoted as the ith component and j is denoted as the jth component).Then,Cjiis the cost of the ith componentrestricted by the jth componentbecause of structural dependence.Therst dependence is described by Cji=Cij=0.The second dependence is described by Cji＞0 and Cij=0.The third dependence is described by Cji＞0 and Cij＞0.As with the cost structural dependence,the time dependence among the components restricted by structural dependence is such that tjiis the time of the ith component restricted by the jth component.

3.2Virtual age of the component after one maintenance action

When one component fails,the component can undergo a minimal maintenance action,imperfect maintenance action,perfect maintenance action,or replacement action.A component that does not fail can undergo a nomaintenance action,imperfect maintenance action,perfect maintenance action,or replacement action.Minimal maintenance actions,imperfect maintenance actions,and perfect maintenance actions can be called repair actions in order to distinguish them from replacement actions.

A minimal maintenance action indicates that the component is“as bad as old”after maintenance,i.e.,the component has the same age it had at the time of failure. A minimal maintenance action only enables the component to work again.A perfect maintenance action restores the component to its original condition after the previous maintenance action.An imperfect maintenance action is betweena minimal maintenanceaction and a perfectmaintenance action,where it improves the performance of the component,but the component is not restored to the condition that was in after the previous maintenance action. After a replacement action,the component is new and its age is zero.With no-maintenance action,the component’s age and performance remain unchanged.

Kijima[31]developed the concept of the virtual age to describe the effect of maintenance wherein a component accumulates age during each period of operation.Each maintenance action“removes”some of the accumulated age for the component.Consider a component in a system such that at any point in time,it is in either of two states, functioning or maintenance,and assume that the component is initially functioning(at time t=0).Assume that n is the number of the components in the system.Let Xndenote the period from the time of the(n−1)th maintenance completionto the start time of the nth maintenance, and let Vndenote the virtual age of the component at the time of the nth maintenance completion.Kijima’s model of the virtual age is given as

where a is some constant,known as the restoration factor,which captures the degree of component restoration achieved through the maintenance action.Using(1),the virtual age can be determined after one maintenance action.The minimal maintenance and no-maintenance actions are denoted as a=0;perfect maintenance is denoted as a=1;imperfect maintenance is denoted as 0＜a＜1; and replacement is denoted as Vn=0.

3.3Choice of maintenance action

The choice of maintenance action depends on the virtual age of the component,the life expectancy of the component,and the age threshold values.Let Vadenote the virtual age of the component,MTBF denote the mean time between failures(i.e.,the life expectancy),and p1,p2denote the age threshold values,0＜ p1≤ p2＜ 1.Set M1=MTBF×p1,M2=MTBF×p2.The process to choose a maintenance action is summarized in Fig.1.

Fig.1 Flowchart of maintenance action choice

3.4Residual life model

Residual life is the remaining lifetime of a component that has survived for a certain amount of time(t′).The mean residual life of any component at a given time is obtained from Tambe[24]and Ebeling[32].The mean residual life of the ith component at a certain duration of time(t′),denoted as MRLi(t′),is given as

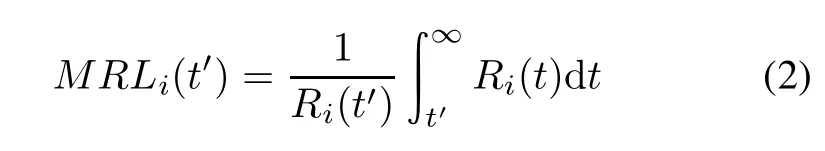
where Ri(t)is the reliability function of the ith component.

The mean time between failures of the ith componentis obtained from

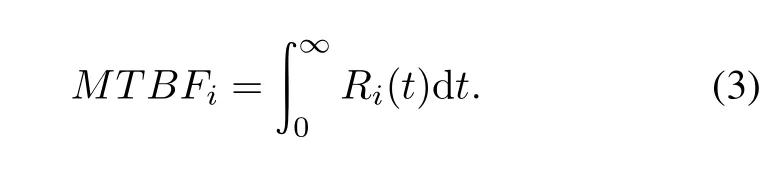
3.5Effect of structural dependence on system downtime and maintenance cost

When many components are maintained together,the system downtime is not simply the sum of the maintenance time of each component.Rather,the system downtime is the sum of the maintenancetimes of the componentsthemselves and the times restricted by the structural dependence.

The maintenancetime for each componentincludes two factors.Oneisthetimerequiredtomaintainthecomponent itself.The other is the times restricted by the structural dependence of the other components.In the case that several components may be restricted by the same single component,if the maintenance strategy considers the structural dependence,only the maximum value of the disassembly times for the same component is counted.If the maintenancestrategydoesnotconsiderthestructuraldependence, the value of the disassembly times for the same component may be repeatedly counted.Let tstibe the maintenance time for the ith component itself,not including the times restricted by the structural dependence.The set Ω ={1,...,i,...,n}is all the components of the system.In a maintenanceproject,let the set G1be the components that need to be maintained,where G1is a subset of Ω.From G1and the structural dependenceamong components denedin Section 3.1,we can obtainthe components in set G2that restrict the components in set G1,where G2is a subset of Ω.

In a maintenance project,taking into consideration the structural dependence,the downtime of the system,denoted by tDW,is determined by(4).The cost that is restricted by the structural dependence,denoted by CSTR, is determined by(5).

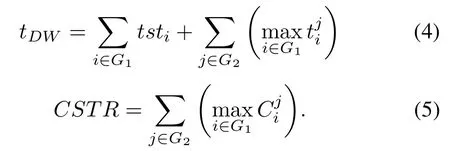
When not considering the structural dependence,the downtime of the system,denoted by tDW,is determined by(6).The cost that is restricted by the structural dependence,denoted by CSTR,is determined by(7).

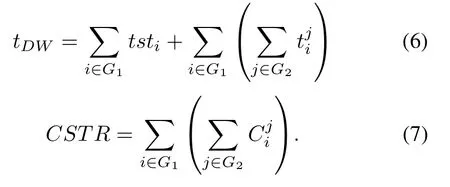
3.6Maintenance cost model for a maintenance project

For a maintenance project,the maintenance cost consists of the constant costs and other varying costs.The constant costs include trafc cost,repairmandispatch,and common tool usage cost.The varying costs include material cost, labor cost,residual life loss,production loss,and cost restricted by the structural dependence.

Let k be the index of the maintenance action.For the kth maintenance project,andare used to denote whether the ith component will be repaired or replaced, respectively.If the ith component will be repaired,then γki=1;otherwise,γki=0.If the ith component will be replaced,then hki=1;otherwise,hki=0.

The kth maintenance project cost is calculated as

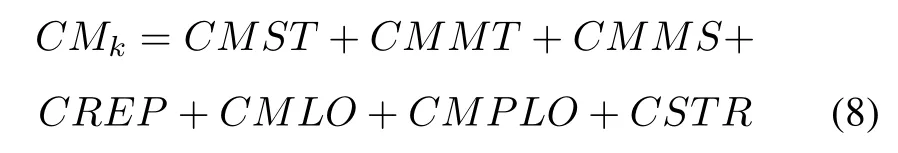
where CMST is the constant cost for one maintenance project,and CMMT is the material cost of all components in the kth maintenance project,which is given as

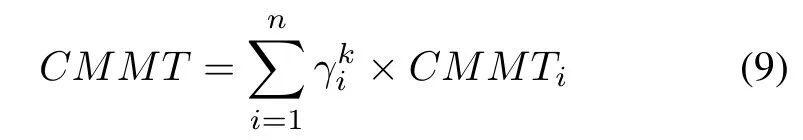
where CMMTiis the material cost for the ith component in one maintenance action.

Thelaborcost ofall componentsinthekth maintenance project,CMMS,is given as

where CMMSRiis the mean labor cost of the ith component in one repair action,and CMMSPiis the mean labor cost of the ith componentin one replacement action.

The purchase cost of the components for the replacement action in the kth maintenance project,CREP,is given as

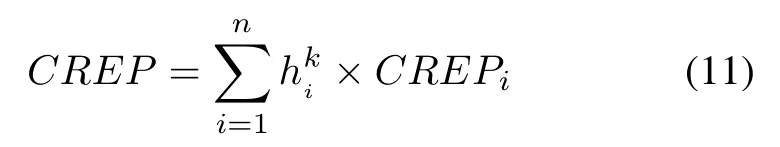
where CREPiis the purchase cost of the ith component.

The residual life loss of all components,CMLO,is given as

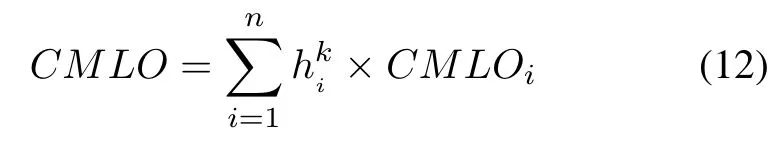
where CMLOiis the residual life loss of the ith component when it is replaced.It can also be expressed as

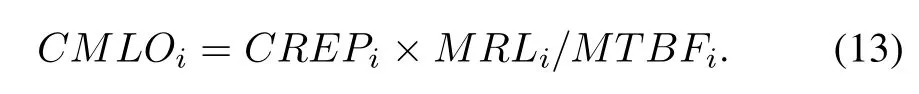
The production loss,CMPLO,is given as

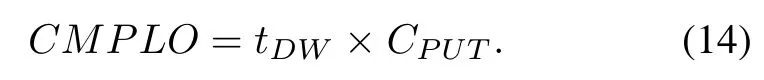
To considerthe structural dependence,the valueof tDWcan be determined by using(4).If the structural dependence is not being considered,the value of tDWcan be determined by using(6).CPUTis the production loss for the system per unit time,which is given in advance.

The cost restricted by structural dependence is CSTR. To consider the structural dependence,the value of CSTR can be determined by using(5).If the structural dependence is not being considered,the value of CSTR can be determined by using(7).

3.7Maintenance strategy optimization

The second method of obtaining an optimal maintenance strategy is chosen in this paper.In an optimal maintenance strategy,the maintenance cost is minimized while the operation availability is not less than some predetermined value.Set the lifetime of the system at Tsim,and U is the numberof maintenanceprojectsoverthelife ofthe system. The maintenance cost over its life is given by

where CMkis the kth maintenance project cost.

The operational availability,A0,is given as

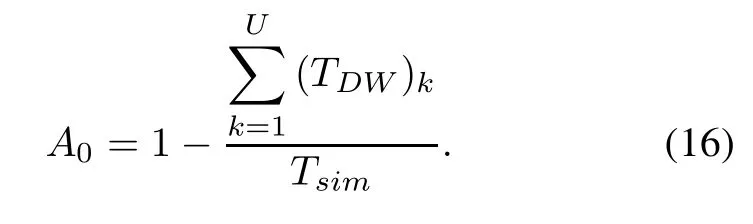
Theoptimalmaintenancestrategyistomakethemaintenancecost,CMT,be the lowest when the operationalavailability,A0,is not less than the minimum operational availability required for the system,AReq.

4.Simulation process and example

In order to illustrate the developed strategy,the Monte Carlo method is used to simulate the maintenance process and obtain the optimal maintenance strategy.The simulation analyzes the differences in the maintenance cost and availability of the system when considering and not considering the structural dependence.

4.1Simulation method

The Monte Carlo method is used to produce the random life of each component and determine the failure time of the system.The maintenance action for each component can be determined according to the virtual age,the life expectancy,and the age threshold values described in Section 3.3.The maintenance cost model described in Section 3.6 can be used to calculate the maintenance cost for a maintenance project.The maintenance strategy optimization method described in Section 3.7 is used to obtain an optimal maintenance strategy.

Firstly,we specify the value of the variables.We specify some global variables,such as n,CMST,CPUT, Tsim,SN,and AReq,where SN is the simulation number needed.For the ith component,we assume that its failure follows a Weibull distribution with a scale parameter αiand a shape parameter βi.For each component,we specify the variables,such as αi,βi,CMMTi,CMMSRi, CMMSPi,and CREPi.We specify the value of Cjiand tji.

Secondly,we make the simulation of maintenance projects for a multi-components system over its life under the given values of a,p1,and p2.

The n random numbers between 0 and 1 are obtained in one simulation of maintenance project.The ith random number in the kth simulation is ξki.The expected time to the next failure from the end of the(k−1)th maintenance projectfortheith componentis denotedbyψki.For a component with a Weibull distribution,ψkican be obtained by

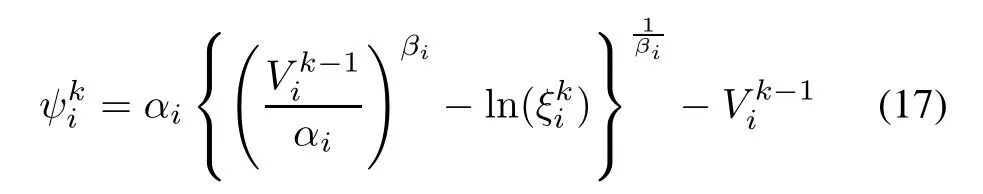
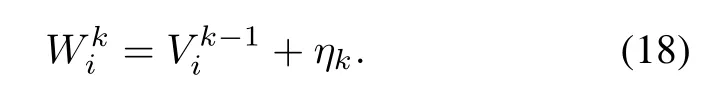
The mean time between failures of the ith component, MTBFi,can be obtained by using(3).The maintenance action of the ith component is determined by the method described in Section 3.3,where Va=Wki,MTBF= MTBFi,and p1,p2are given in advance.

In the initial state,the age of each component is zero; that is,After one maintenance project,the age for each component is updated by

From(8)–(14),constant cost,material cost,labor cost, residual life loss,production loss,and cost affected by structural dependence for the kth maintenance project can be obtained.The total maintenance cost for the kth maintenance project,CMk,can be calculated.

When the system life in the simulation process exceeds Tsim,thesimulationofthemaintenanceprojectsinthesystem’s life stops;otherwise,the n randomnumbersbetween 0 and 1 are obtainedagainforthe nextmaintenanceproject simulation.The abovesimulation process is the simulation process for all maintenance projects in the life of the system.It can be executed multiple times to get more accurate simulation results.For each a,p1,and p2,the total simulation process is summarized in Fig.2.

Finally,an optimal maintenance strategy can be obtainedbythesimulation.Thetotalmaintenancecost within the life of the system is given by(15).The operation availability,A0,is given by(15).To get the optimal maintenance strategy,let a change from 0.1 to 0.9,let p1change from 0.1 to 0.9,and let p2change from p1to 0.9.The lowest maintenance cost with the restraint,A0,that considers or does not consider the structural dependence can be obtained.

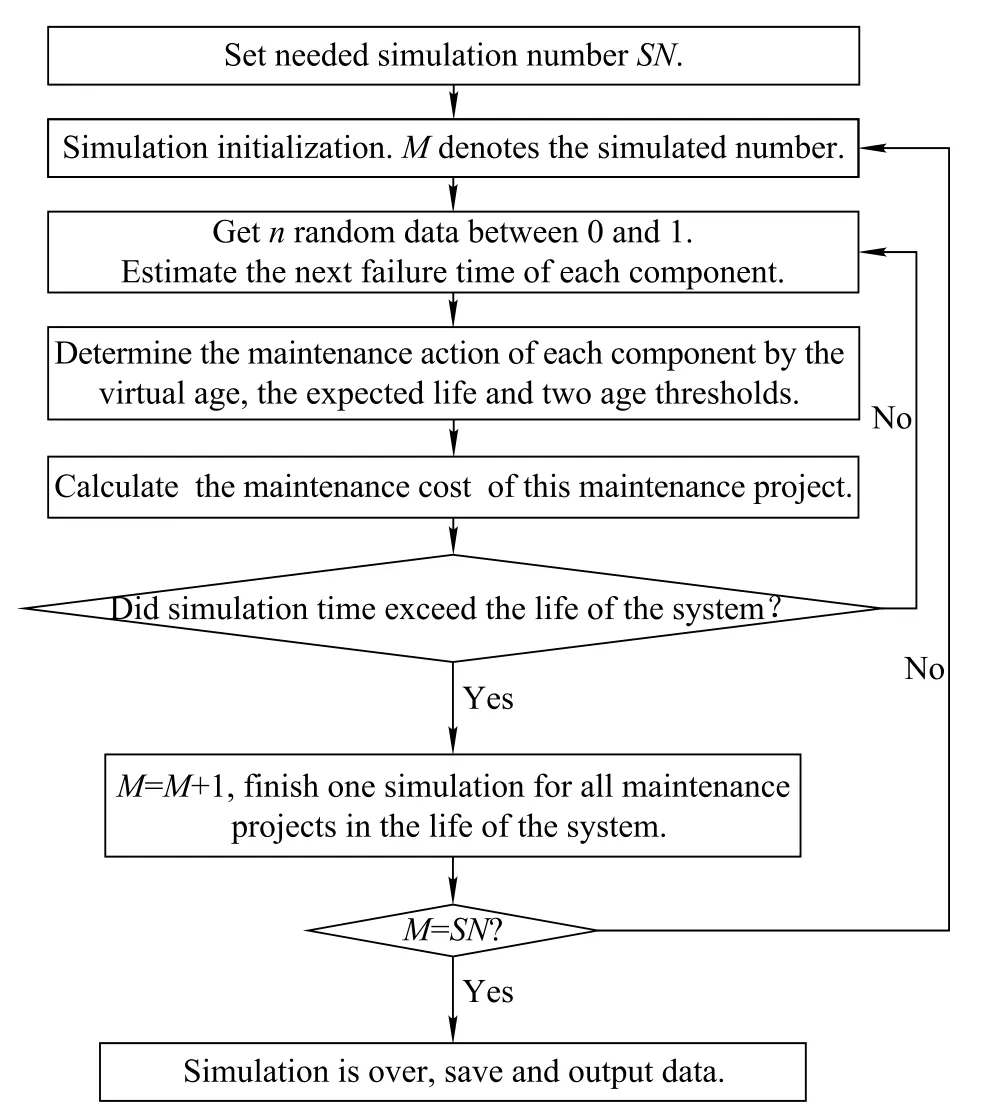
Fig.2 Flowchart of the simulation

4.2Simulation example

The structure of an example system is shown in Fig.3.

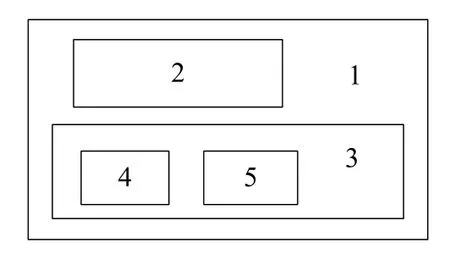
Fig.3 The structure of an example system

The structural cost and the structural time among the components are as follows:C12=C13=100 dollar, C34=C35=200 dollar,t12=t13=1 h,and t34=t35= 2 h.Basic parameters for each component of the system are described in Table 1.

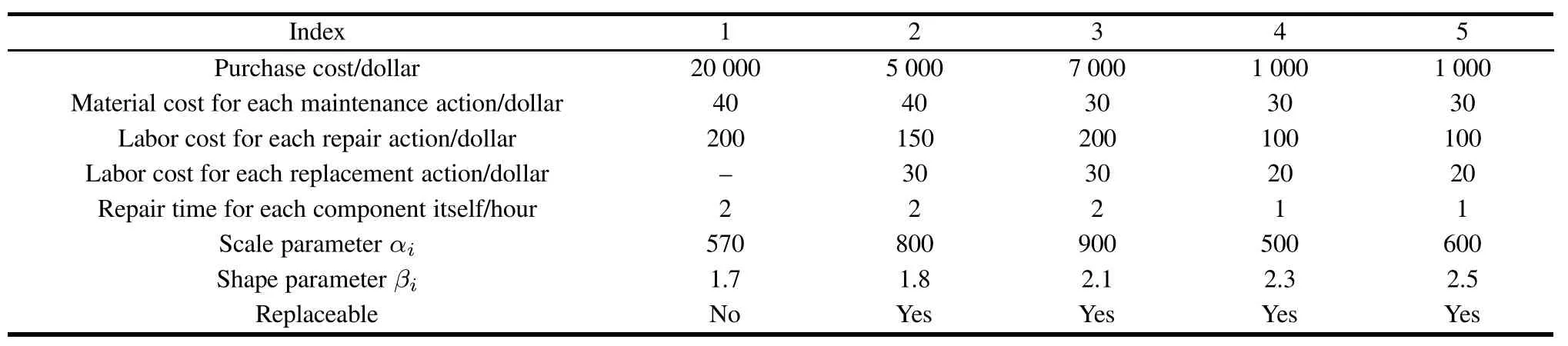
Table 1 Basic parameters of each component of the system

The constant cost for each maintenance project was 100 dollar.The availability of the system was no less than 0.95. Theloss ofproductionin unittime was 500dollarper hour. The life of the system was set at 10 000 h.Using Microsoft Excel 2007 and Microsoft Visual Basic to simulate the opportunistic maintenance process,the values of p1,p2,and a wererst determined from the domain of the parameters of p1,p2,and a.The degree of variance was 0.1 for the parameters p1,p2,and a.For each maintenance strategy with respect to p1,p2,and a,1 000 Monte Carlo simulations were performed that considered the structural dependence and 1 000 Monte Carlo simulations were performed that did not consider the structural dependence.This resulted in two mean maintenance cost values of the system in its lifetime.

For a constant restoration factor value,if we change the values of p1and p2,the minimum maintenance cost under the constant restorationfactor value can be obtained.Fig.4 describes the relation between the minimum maintenance cost and the restorationfactor.The simulation results show that the maintenancecost is greater when the structural dependence is not considered than when it is.

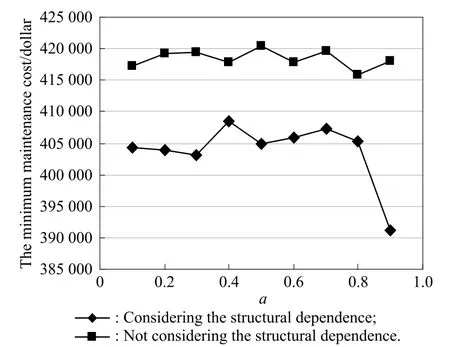
Fig.4 The minimum maintenance costs at different restoration factors

When we make a=0.6 and p1=0.2,and p2changes from 0.2 to 0.9,we can obtain the different maintenance costs with changes in p2.Fig.5 describes the relation between the maintenance cost and p2at constants a and p1. The maintenance cost is greater when the structural dependenceis notconsideredthanwhenit is.Whenp2＜0.6,for thecomponent,theageofwhichis less than0.6×MTBF, an imperfect maintenance action would require the lower maintenance cost than a replacement action,because more than 60%of its residual life is lost in a replacement action. With an increase in p2,the probability of imperfect maintenance increases,and the probability of a replacement action decreases;thus,the maintenance cost decreases.At p2=0.6,the cost value reaches a minimum.However,a component whose age is more than 0.6×MTBF would benet more from a perfect maintenance or replacement action than an imperfect maintenance action.With a continuous increase in p2,the probability that some componentswithgreateragewouldbe selectedtoundergoperfect maintenance or replacement decreases;thus,the maintenance cost of the system increases slowly over its life.

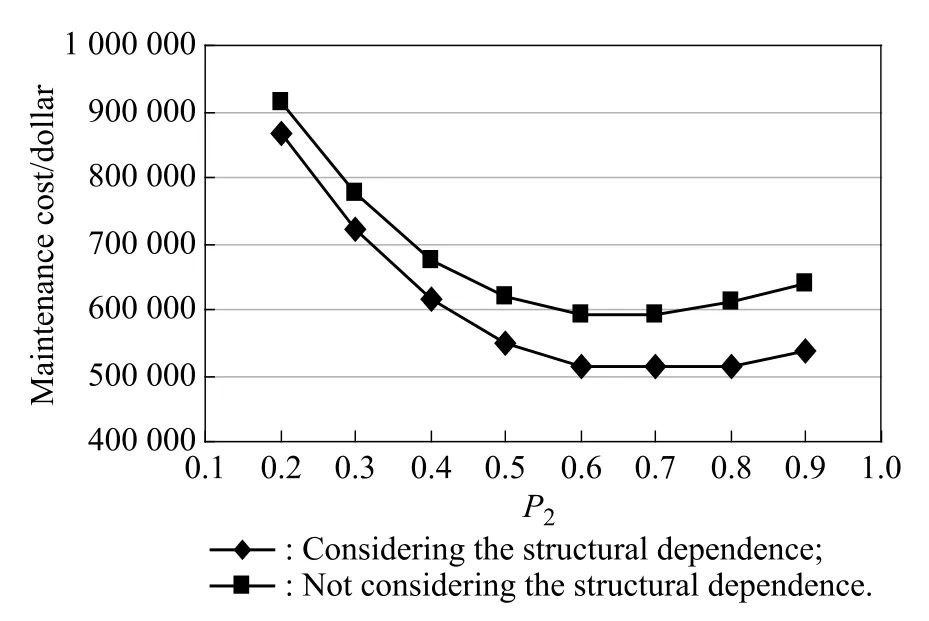
Fig.5 Maintenance costs with p2at constants a and p1

When we make a=0.6 and p2=0.9,and p1changes from 0.1 to 0.9,we can obtain the different maintenance cost with changes in p1.Fig.6 describes the relation between the maintenance cost and p1at constants a and p2. The maintenance cost is greater when structural dependence is not considered than when it is.Both curves decrease with an increase in p1.This indicates that increasing the probability of a minimal maintenance action or nomaintenance for components in an opportunistic maintenance strategy can decrease the maintenance cost of the system.

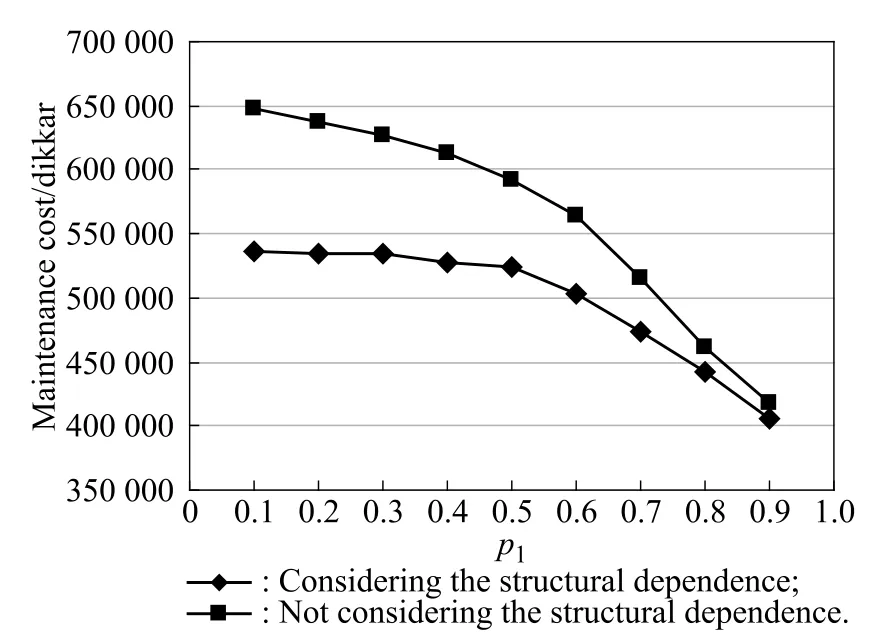
Fig.6 Maintenance costs with p1at constants a and p2

Fig.7 Availability with p1at constant aand p2

5.Conclusions

An opportunistic maintenance strategy that considers the structural dependence and economic dependence for a multi-component system is developed in this paper.The cost relation and time relation among components based on structural dependence are developed,and these relations are put into an opportunistic maintenance strategy. The choice of a maintenanceaction for a componentbased on the virtual age of the component,the life expectancy of the component,and the age threshold values is established.Combiningthe results from several studies,a maintenance cost breakdown structure is established,which includes material cost,labor cost,residual life loss,production loss,cost restricted by the structural dependence,and the constant cost for each maintenance project.

The Monte Carlo simulation process is utilized to obtain an optimal opportunisticmaintenance strategy.The simulation shows that the minimum maintenance cost is less when the structural dependence is considered than when it is not considered at the same restoration factor,and the correspondingavailability is larger when the structural dependenceisconsiderediftheotherconditionsarethesame. The results show that the developed opportunistic maintenancestrategythatconsidersstructuraldependenceismore accurate and cost-effective than one that does not,which can help optimize an opportunistic maintenance strategy.

Acknowledgements

The authors would like to thank Kelly Smith and Mark Zimmerman for their edits and to acknowledge the anonymous reviewers for their constructive comments,which have made it possible to improve the quality of this paper.

[1]M.Bevilacqua,M.Braglia.The analytic hierarchy process applied to maintenance strategy selection.Reliability Engineering and System Safety,2000,70(1):71–83.

[2]L.C.Thomas.A survey of maintenance and replacement models of multi-item systems.Reliability Engineering,1986, 16(4):297–309.

[3]R.Radner,D.W.Jorgenson.Opportunistic replacement of a single part in the presence of several monitored parts.Management Science,1963,10(1):70–84.

[4]J.J.McCall.Operating characteristics of opportunistic replacement and inspection policies.Management Science, 1963,10(1):85–97.

[5]A.N.Rao,B.Bhadury.Opportunistic maintenance of multiequipment system:a case study.Quality and Reliability Engineering International,2000,16(6):487–500.

[6]M.Berg.Optimal replacement policies for two-unit machines withincreasing running costs 1.Stochastic Processes and their Applications,1976,5(1):89–106.

[7]G.Kumar,V.Jain,O.P.Gandhi.Steady-state availability analysis of repairable of repairable mechanical systems with opportunistic maintenance by using Semi-Markov process.International Journal of System Assurance Engineering Management,2014.doi:10.1007/s13198-014-0231-8.

[8]D.A.Savic,G.A.Walters,J.Knezevic.Optimal opportunistic maintenance policy using genetic algorithms,1:formulation. Journal of Quality in Maintenance Engineering,1995,1(2): 34–49.

[9]L.Cui,H.Li.Opportunistic maintenance for multi-component shock models.Mathematical Methods of Operations Research, 2006,63(3):493–511.

[10]Z.Cheng,Z.Yang,B.Guo.Optimal opportunistic maintenance model of multi-unit systems.Journal of Systems Engineering and Electronics,2013,24(5):811–817.

[11]Y.Zhou,Z.Zhang,T.Bin,et al.Maintenance optimization of a multi-state series-parallel system considering economic dependence and state-dependent inspection intervals.Reliability Engineering and System Safety,2013,111:248–259.

[12]W.Derigent,E.Thomas,E.Levrat,et al.Opportunistic maintenance based on fuzzy modeling of component proximity. CIRP Annals-Manufacturing Technology,2009,58(1):29–32.

[13]T.Bedford,I.Dewan,I.Meilijson,et al.The signal model:a model for competing risks of opportunistic maintenance.European Journal of Operational Research,2011,214(3):665–673.

[14]T.Bedford,B.M.Alkali.Competing risks and opportunistic informative maintenance.Proceedings of the Institution of Mechanical Engineers–Part O:Journal of Risk and Reliability, 2009,223(4):363–372.

[15]J.Cai,H.Zuo,D.Lv.Availability simulation of multicomponent system based on opportunity maintenance policy. Transactions of Nanjing University of Aeronautics and Astronautics,2009,26(3):219–223.

[16]F.Ding,Z.Tian.Opportunistic maintenance optimization for wind turbine systems considering imperfect maintenance ac-tions.International Journal of Reliability,Quality and Safety Engineering,2011,18(5):463–481.

[17]J.Hu,L.Zhang,W.Liang.Opportunistic predictive maintenance for complex multi-component systems based on DBNHAZOP model.Process Safety and Environmental Protection, 2012,90(5):376–388.

[18]F.Ding,Z.Tian.Opportunistic maintenance for wind farms considering multi-level imperfect maintenance thresholds.Renewable Energy,2012,45(1):175–182.

[19]M.Asjad,S.Mohite,M.S.Kulkarni,et al.Opportunistic action for subassemblies of a reciprocating compressor:an LCC based approach.International Journal of Performability Engineering,2013,9(3):273–285.

[20]J.P.Varghese,G.Kumar.Availability analysis with opportunistic maintenance of a two component deteriorating system. International Journal of Materials,Mechanics and Manufacturing,2014,2(2):155–160.

[21]R.Laggoune,A.Chateauneuf,D.Aissani.Opportunistic policy for optimal preventive maintenance of a multi-component system in continuous operating units.Computer and Chemical Engineering,2009,33(9):1499–1510.

[22]J.Hu,L.Zhang.Risk base opportunistic maintenance model for complex mechanical systems.Expert Systems with Applications,2014,41(6):3105–3115.

[23]J.Koochaki,J.A.C Bokhorst,H.Wortmann,et al.Condition based maintenance in the text of opportunistic maintenance. International Journal of Production Research,2012,50(23): 6918–6929.

[24]P.P.Tambe,S.Mohite,M.S.Kulkarni.Optimizationof opportunistic maintenance of a multi-component system considering theeffect of failures onqualityand production schedule:acase study.International Journal of Advanced Manufacturing Technology,2013,69(5/8):1743–1756.

[25]D.Ait-Kadi,J.B.Menye,H.Kane.Resources assignment model in maintenance activities scheduling.International Journal of Production Research,2011,49(22):6677–6689.

[26]B.K.Lad,M.S.Kulkarni.Optimal maintenance schedule decision for machine tools considering the user’s cost structure. International Journal of Production Research,2012,50(20): 5859–5871.

[27]H.Pham,H.Z.Wang.Optimal(τ,T)opportunistic maintenance of a k-out-of-n:G system with imperfect PM and partial failure.Naval Research Logistics,2000,47(3):223–239.

[28]H.Z.Wang,H.Pham.Reliability and optimal maintenance. New York:Springer,2006.

[29]X.Zheng,N.Fard.A maintenance policy for repairable system based on opportunistic failure-rate tolerance.IEEE Trans. on Reliability,1991,40(2):237–244.

[30]W.Hou,Z.Jiang.An opportunistic maintenance policy of multi-unit series production system with consideration of imperfect maintenance.Applied Mathematics and Information Sciences,2013,7(1):283–290.

[31]M.Kijima.Some results for repairable system with general repair.Journal of Applied Probability,1989,26(1):89–102.

[32]C.E.Ebeling.An introduction to reliability and maintainability engineering.New Delhi:MaGraw-Hill,2010.

Biographies

Junbao Geng was born in 1973.He received his Ph.D.degree in thermal engineering from the Huazhong University of Science and Technology, Wuhan,China,in 2007.He is currently an associate professor in College of Power Engineering at the Naval University of Engineering,Wuhan, China.His research interests mainly include life cycle costing,reliability and maintainability.

E-mail:gengjb2002@163.com

Michael Azarian received his Ph.D.degree in materials science and engineering from Carnegie Mellon University.He is currently a research scientist of the Center for Advanced Life Cycle Engineering at the University of Maryland,College Park,USA.His interests mainly include materials science,photonic devices,and reliability.

E-mail:mazarian@calce.umd.edu

Michael Pecht received his Ph.D.degree in engineering mechanics from the University of Wisconsin at Madison.He is currently a chair professor in Mechanical Engineering and a professor in applied mathematics at the University of Maryland,College Park,USA.His interests mainly include prognostics and health management,reliability and supply chain policies.

E-mail:Pecht@calce.umd.edu

10.1109/JSEE.2015.00057

Manuscript received June 30,2014.

*Corresponding author.

This work was supported by the Postdoctoral Science Foundation of China(20080431380).