Fast multi-parameter estimation and localization for MIMO radar

Lingyun Xu,Xiaofei Zhang,and Miao Yu

1.College of Science,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;

2.Nanjing Telecommunication Technology Institute,Nanjing 210007,China

Fast multi-parameter estimation and localization for MIMO radar

Lingyun Xu1,2,*,Xiaofei Zhang1,and Miao Yu2

1.College of Science,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;

2.Nanjing Telecommunication Technology Institute,Nanjing 210007,China

This paper addresses the problem of four-dimensional angle and Doppler frequency estimation for bistatic multiple-input multiple-output(MIMO)radar with arbitrary arrays in spatial colored noise.A novel method for joint estimation of Doppler frequency,two-dimensional(2D)direction of departure and 2D direction of arrival based on the propagator method(PM)for arbitrary arrays is discussed.A special matrix is constructed to eliminate the inuence of spatial colored noise.The four-dimensional(4D)angle and Doppler frequency are extracted from the matrix and the threedimensional(3D)coordinates of the targets are then calculated on the basis of these angles.The proposed algorithm provides a lower computational complexity and has a parameter estimation very close to that of the ESPRIT algorithm and the DOA-matrix algorithm in the high signal to noise ratio and the Cram´er-Rao bound (CRB)is given.Furthermore,multi-dimensional parameters can be automatically paired by this algorithm to avoid performance degradation resulting from wrong pairing.Simulation results demonstrate the effectiveness of the proposed method.

four-dimensional(4D)angle estimation,Doppler frequency estimation,propagator method(PM),multiple-input multiple-output(MIMO)radar,arbitrary array,spatial colored noise.

1.Introduction

Multiple-inputmultiple-output(MIMO)radar is an emergingtechnologythat is attractingtheattentionofresearchers and practitioners alike[1–4].An MIMO radar system can transmit multiple probing signals via its antennas that may bechosenquitefreely.This waveformdiversityenablessuperior capabilities compared with a standard phased array radar[5–8].By exploiting the spatial diversity,the statistical MIMO radar,whose transmit(or both transmit and receive)antennas are spaced far away from each other,can overcomeperformancedegradationscaused by target scintillations.UnlikethestatisticalMIMOradar,theco-located MIMO radar whose elements in transmit and receive arrays are closely spaced,can achieve the coherent processing gain.Furthermore,the coherent MIMO radar includes monostatic MIMO radar and bistatic MIMO radar based on the placement geometry of transmit and receive antennas.In this paper we mainlydiscuss a bistatic MIMO radar architecture,whose parameter estimation is considered extensively.

Angle estimation algorithms for MIMO radar have been studied which contain estimation of signal parameters via the rotational invariance techniques(ESPRIT)algorithm, multiple signal classication(MUSIC)algorithm,Capon algorithm,propagator method(PM)algorithm,parallel factor(PARAFAC)algorithm and so on[8–14].However,the mentioned papers did not discuss the Doppler frequency estimation,and the noise was supposed to be the Gaussian white noise.The direction of departuredirection of arriral(DOD-DOA)and Doppler frequency estimation for the MIMO radar was investigated in[15–18].Eigenvaluedecompositionofthecross correlationmatrix was required to obtain signal subspace or noise subspace in[15,16].Li and Zhang proposed the quadrilinear decomposition algorithm for angle and Doppler frequency estimation,and the algorithm includes iterative methods,which require a higher complexitythan subspace methods[17].Unfortunately,they cannot remove the effect of spatial colored noise.Although Xu et al.proposed the angle and Dopplerfrequencyestimationalgorithm[18] which can eliminate the inuence of spatial colored noise, it was aimed at a uniform linear array model.In practical applications the geometric structure of the array is often varied and irregular.The aim of this paper is to develop a low-complexity PM-based angle and Doppler frequency estimation algorithm based on arbitrary arrays forthe MIMO radar.The three-dimensional(3D)coordinates of the targets are then obtained by the estimated fourdimensional(4D)angle.The proposedalgorithmhas lower computational complexity and very close parameters estimation performance compared to the ESRPIT algorithm in a high sinal to noise ratio(SNR).And it pairs the parameters automatically without array aperture loss and the inuence of the spatial colored noise can be eliminated. We also present numerical results for different targets and a variety of data lengths.Simulation results illustrate the performance of the proposed algorithm.

The operation(.)†,(.)T,(.)H,(.)−1and vec[.]denote pseudo-inverse,transpose,conjugate-transpose,inverse operations and vectorization operator,respectively.‖ ‖Frepresents Forbenius norm;IKis a K×K identity matrix;⊗and⊙aretheKroneckerproductandKhatri-Rao product.

2.Data model

Consider a narrowband bistatic MIMO radar system with botharbitraryarraysfor its transmit/receivearrayas shown in Fig.1,in which M sensors are arranged in the transmit array with half-wavelength spacing.The structure of the receive array is similar with that of the transmit array,and N sensors are arranged.We dene the location of the mth sensor in the transmit array as(xtm,ytm) (m = 1,2,...,M),and the location of the nth sensor in the receive array as(xrn,yrn)(n=1,2,...,N). The transmit sensors transmit M orthogonal coded signals.The transmitted baseband coded signals are denoted by sm∈C1×P,where m denotes the mth transmitter,and P is the length of the transmitted code.We assume that there are K uncorrelated targets,and the received array through reections of the target can be expressed as

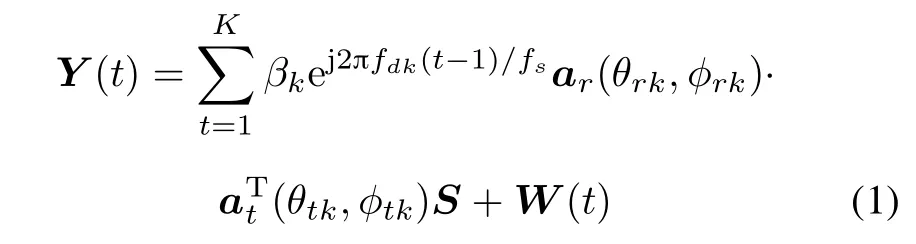
where fdkand βkdenote Doppler frequency and radar cross section(RCS)of the kth target respectively,fsis the pulse repeat frequency,and ar(θrk,φrk)and at(θtk,φtk) are the receive steering vector and the transmit steering vector of the kth target.

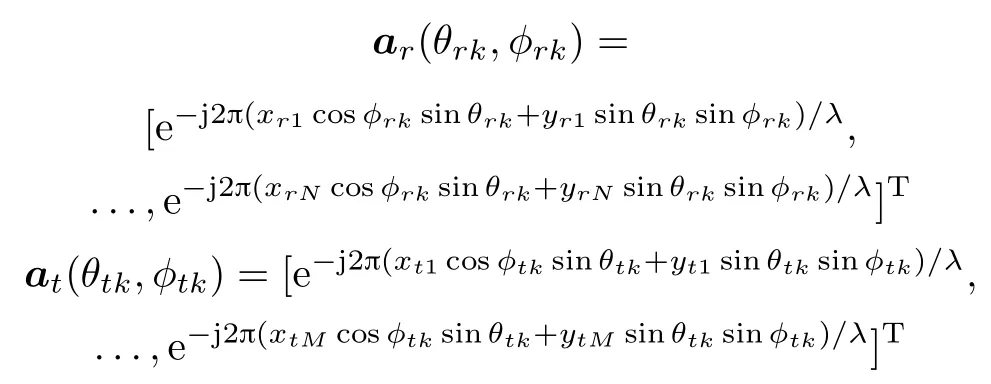
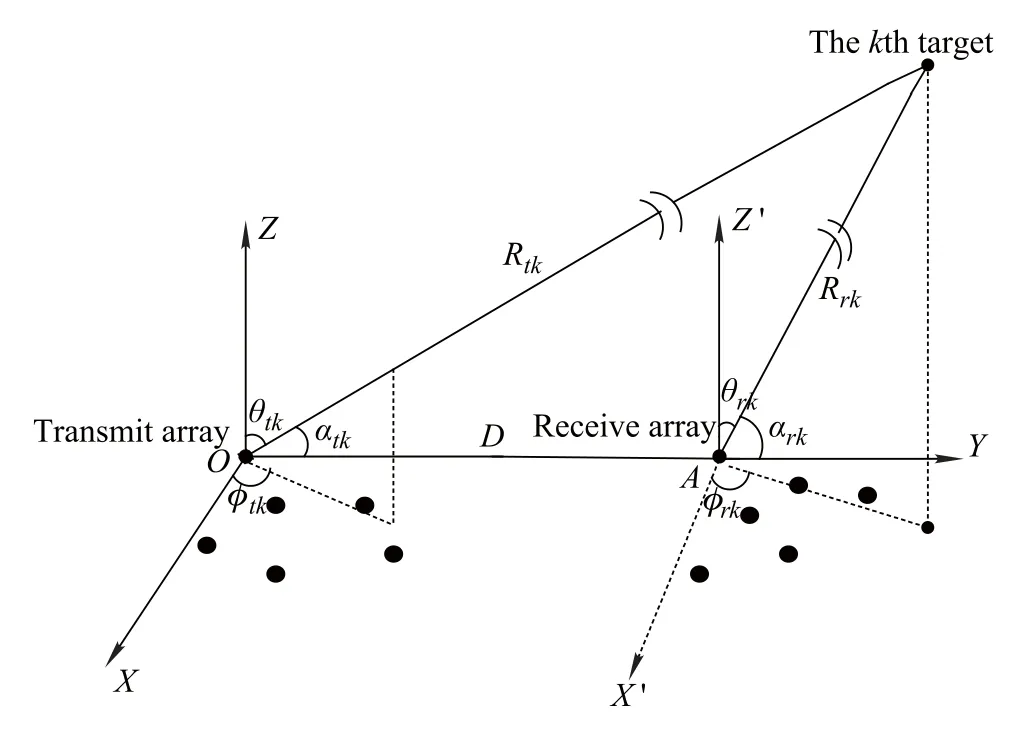
Fig.1 Bistatic MIMO radar scenario

O and A are the reference points of the transmit array and the receive array.The length of the baseline OA is D.αtkand αrkare the angles between the target connected to the transmit/receive station and the Y axis positive direction respectively.S=[s1,s2,...,sM]Tanddenotes a Gaussian noise ofzeromeanwithunknowncovariancematrixQw.Matchingthereceiveddatawiththesignalweobtain

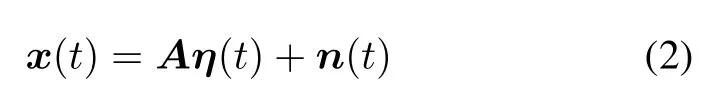
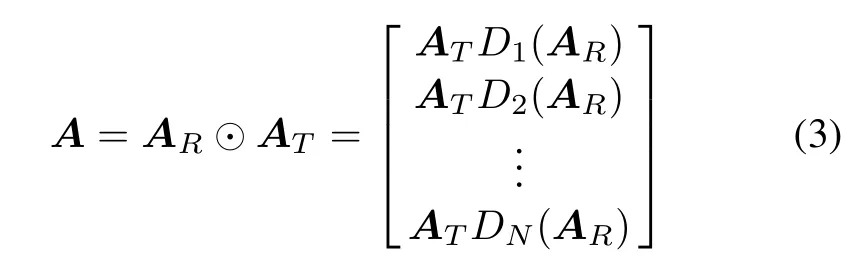
where Dn(.)is to extract the nth row of its matrix argument and construct a diagonal matrix out of it[13].AT= [at(θt1,φt1),at(θt2,φt2),...,at(θtK,φtK)]∈ CM×K, AR=[ar(θr1,φr1),ar(θr2,φr2),...,ar(θrK,φrK)]∈CN×K.We assume at(θtk,φtk)and ar(θrk,φrk)are constant for L samples,and denex(2),...,x(L)],which can be expressed as

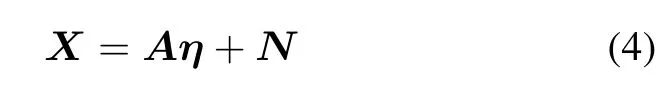
where η = [η(1),η(2),...,η(L)],N = [n(1), n(2),...,n(L)]is the noise matrix.

3.Multi-dimensional parameters estimation algorithm in spatial colored noise

Let X1=[x(1),x(2),...,x(L−1)]=Aη1+N1, X2=[x(2),x(3),...,x(L)]=Aη2+N2,where η1=[η(1),η(2),...,η(L−1)],η2=[η(2),η(3),..., η(L)],N1=[n(1),n(2),...,n(L−1)],N2=[n(2), n(3),...,n(L)].The covariance matrix of n(t)is as follows:

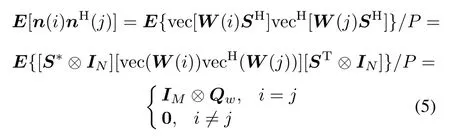
which shows that the cross-covariancematrix of noise is 0. This characteristic will be utilized in this paper to improve the estimate performance.

Note that η2= Φη1,Φ =diag[ej2πfd1/fs,ej2πfd2/fs, ...,ej2πfdK/fs],N2NH1/(L−1)=0.The covariancematrix of X1and X2can be written as follows:

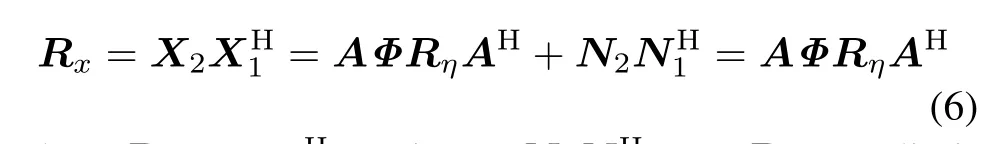
where Rη=η1ηH1.Owing to N2NH1=0,Rxcan eliminatetheinuenceofspatialcolorednoise.Sinceand the relationshipwe construct the special matrix R by utilizing(6),

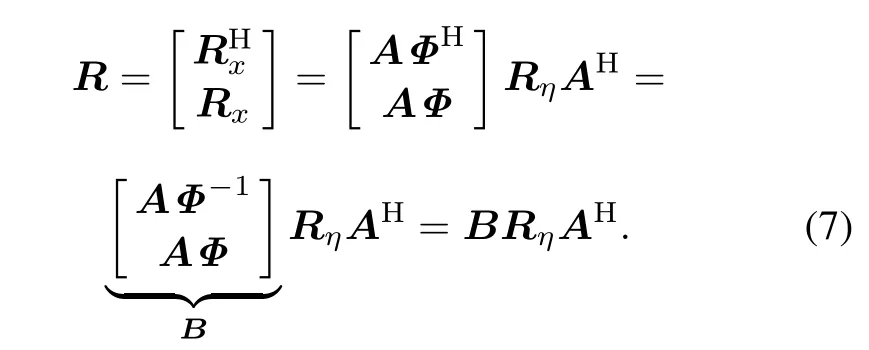
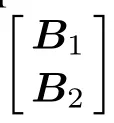
The optimal solution of the propagator matrix V is given by V =(R1RH1)−1R1RH2.We dene a new matrix ˜V =[IK,VH]T,where IKis the identity matrix.According to˜V and(8),we obtain

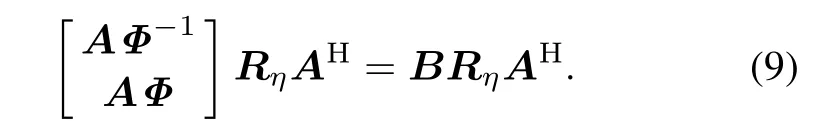
Equation(9)can be rewritten as

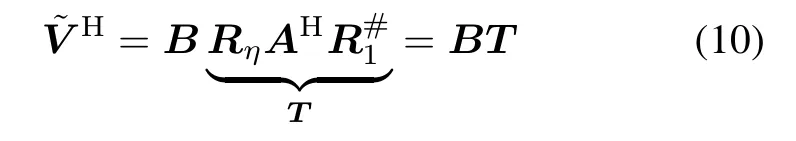
where R#1is the pseudo inverse of R1,and T is a nonsingular matrix.From(10),the columns inspan the same signal subspace as the column vectors in B.Thus the signal subspace can be obtained by avoiding the eigendecomposition of the sample covariance matrix.Then the matrixcan be partitioned into two submatrices,i.e.Thus we get

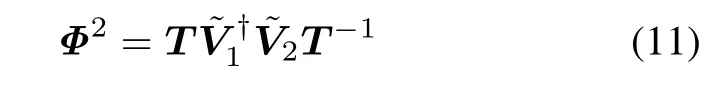
which shows that the main diagonal elements of Φ2equal the eigen-values obtained via the eigen-decomposition ofwith T as the corresponding eigenvectors.Thus we can calculate the Doppler frequency of the kth target as follows:

where ϕkis the kth diagonal element of Φ2,angle(·)denotes the phase of a complex.Then we can get the matrix ˆA from

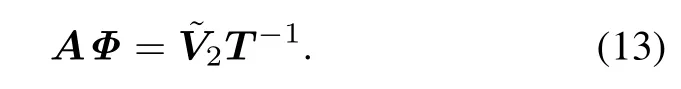
Because Φ is the diagonal matrix,it cannot affect the estimation of 2D-DOD and 2D-DOA using the least square method from the matrix.We note that the 4D angle and Doppler frequencies are given through the corresponding eigenvectors.Thus the multi-parameters pairing is automatically obtained.

3.1Estimation of 4D angle

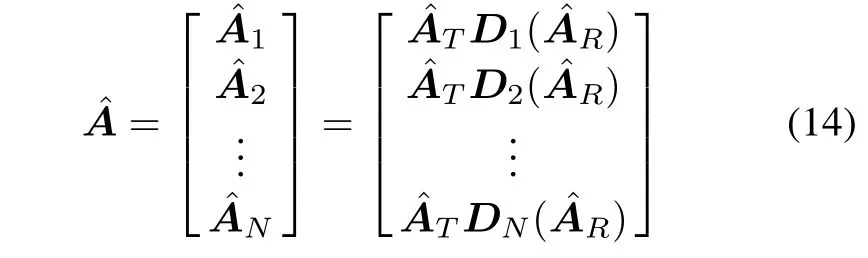
where Φ1= diag[exp(j2πmr1w21+nr1v21)/λ,..., exp(j2πmrKw21+nrKv21)/λ],mrk=sinθrkcosφrk, nrk=sinθrksinφrk,w21=xr1−xr2,v21=yr1−yr2. Φ2= diag[exp(j2πmr1w32+nr1v32)/λ,..., exp(j2πmrKw32+nrKv32)/λ],w32=xr2−xr3,v32=yr3−yr2.The eigenvalueofWe take the diagonal elements ofto construct a vectorcan be obtained viaand we take the diagonal elements ofto construct a vectorSimilarly,we can also getand form the following matrix

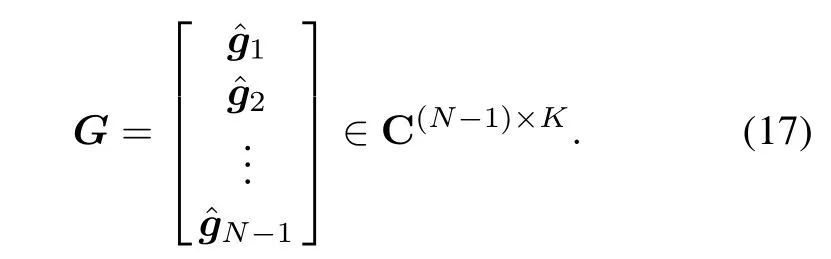
rkis the kth column of G,and C=angle(rk).Assuming the spacing between adjacent elements of the receive array is no more than half wavelength,C will be in(−π,π),and there will be no phase ambiguity with

C can also be denoted as

where

We can use the least square principle to get the solution of ˆmrk,ˆnrk:

Then 2D-DOA can be estimated via

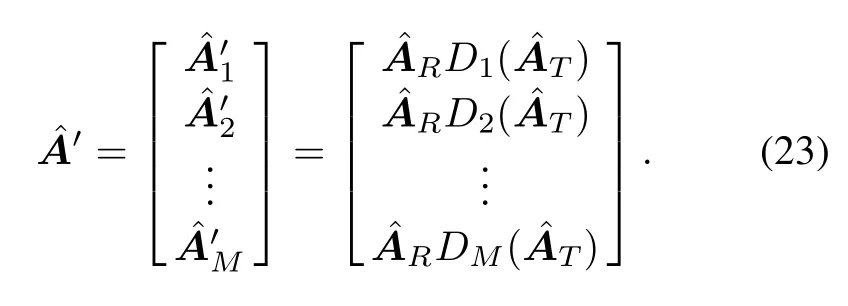
Similarly,we can imitate the process(14)–(22).Thus the 2D-DOD can be estimated via

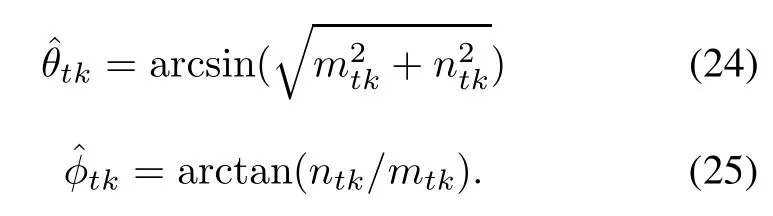
Now we show the major steps of the proposed algorithm as follows:

(i)Compute the covariance matrix of the received data through(6)and construct a new matrix according to(7).

(ii)Estimate the propagator V from(8).

(iii)Compute the Doppler frequency according to(11) and(12).

(iv)Estimate the matrix A from(13),then use the least square method to estimate DOD and DOA.

(v)The 2D-DOA can be estimated from(14)–(21)and similarly the 2D-DOD can be obtained through(24)–(25).

3.23D coordinates of the targets

The relationship between the estimated 4D angle and 3D coordinates of the target(xk,yk,zk)(k=1,2,...,K)is as follows according to Fig.1:

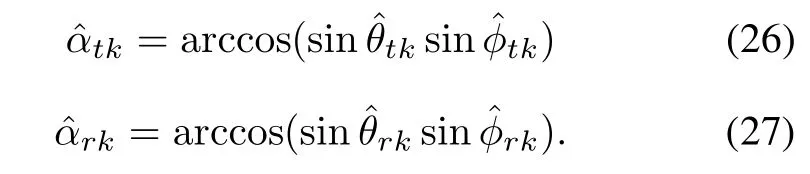
According to the law of sine,we can get

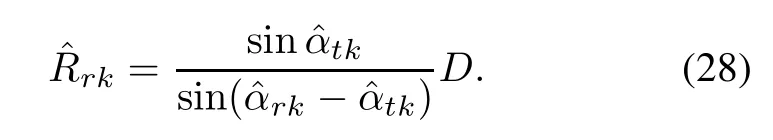
Then the coordinate of the target can be obtained.

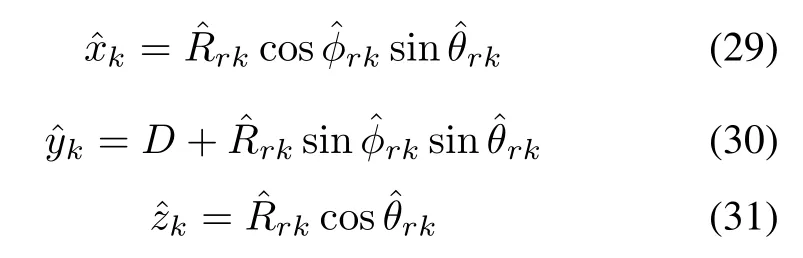
It can be observed that 3D coordinates of the targets are determinedby the4D anglesestimated aboveandthebaseline of the bistatic radar.

3.3Complexity analysis

In contrast to the ESPRIT algorithm[15],our algorithm has a low computational load.The main computational cost of our algorithm is the estimation of the matrix˜VH, which takes O(2M2N2K+MNK2+K3).The computational complexity of our algorithm is O((L−1)M2N2+ 2M2N2K+3MNK2+2K3−MK2−NK2),while the ESPRIT algorithm[15]requires O((L−1)M2N2+ 12M3N3+MNK2+M(N−1)K2+N(M−1)K2), and the DOA matrix algorithm[16]requires O(3(L−

2)M2N2+2M3N3+(N−1)MK2+(M−1)NK2).Fig.2shows the complexity comparison with M=9,N=9, K=3 and different Ls.From Fig.2 wend that our algorithm has much a lower computational load than the ESPRIT algorithm[15]and the DOA matrix algorithm of Cao[16].

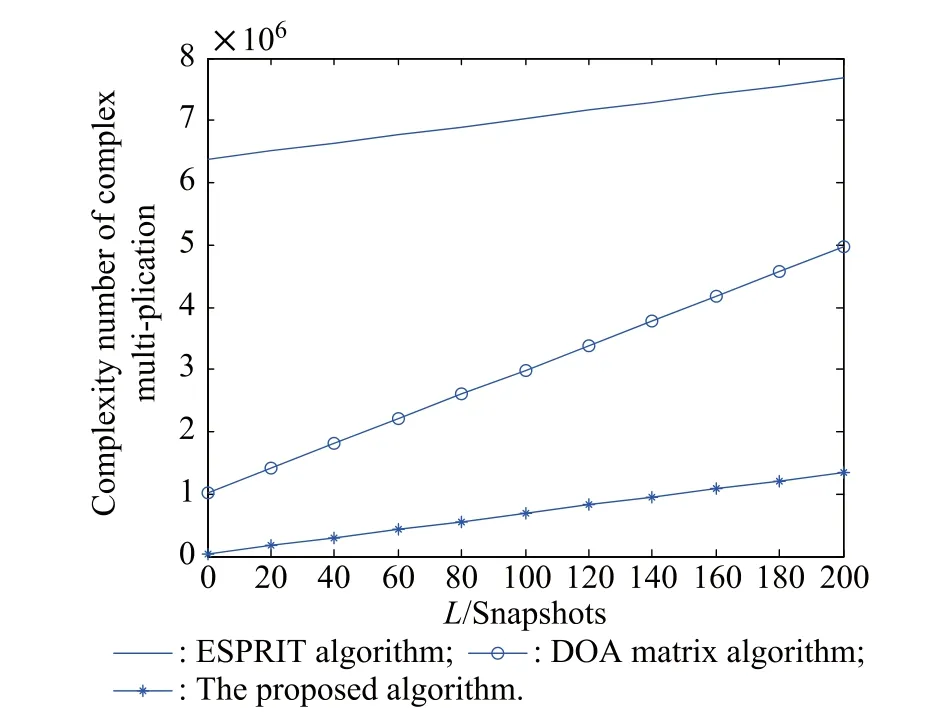
Fig.2Complexity comparison with M=9,N=9,K=3 and different Ls

4.Simulation results

We present the Monte Carlo simulations to assess the parameter estimation performance of our algorithm.Dene the root mean squared error(RMSE)as

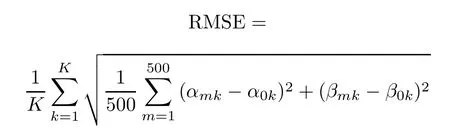
where αmkand βmkare the estimates of elevation angle α0kand azimuth angle β0kof the kth target relative to the transmit/receive array of the mth Monte Carlo trial.

Note that M,N,L and K are the number of transmit sensors,the receive sensors,the snapshots of the targets,respectively.We assume that there are K=3 non-coherenttargets,which are located atangles (θt1,φt1,θr1,φr1) = (25°,20°,30°,30°), (θt2,φt2, θr2,φr2)= (50°,30°,40°,35°),(θt3,φt3,θr3,φr3)= (70°,40°,50°,45°),respectively.The Doppler frequencies of the three targets are 1 000 Hz,1 500 Hz and 2 100 Hz,respectively,and their RCSs are given by β1=β2= β3=1.The pulse repeat frequency fsis 10 kHz for an M=9 and N=9 bistatic MIMO radar.The length of baseline D is equal to 50 km.Figs.3–4 shows the estimation results with 50 Monte Carlo trials at L=100 and SNR=20 dB.The performance of the estimated parameters is plotted in Fig.3.Fig.4 shows the 3D coordinates estimate performance.As seen in Figs.3–4,the 2D-DOD, 2D-DOA and Doppler frequencies of all three targets are paired correctly and well localized.

Fig.3 Angle and Doppler frequency estimation at SNR=20 dB

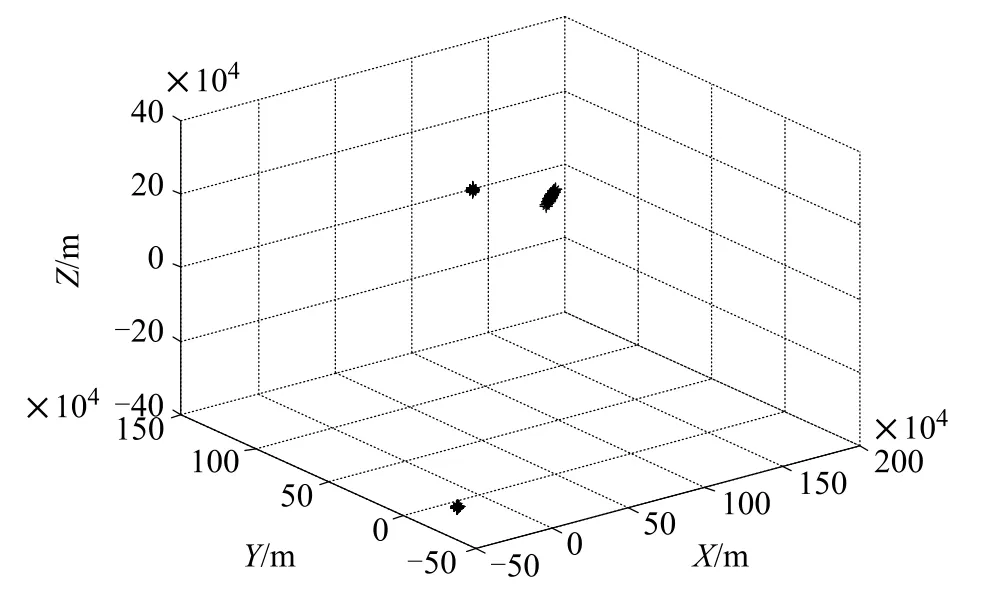
Fig.4 Coordinates of the three targets

Figs.5–7 present the angle and Doppler frequency es-timation performance comparison with M=9,N=9, K=3 and L=100,where we compare our algorithm with the ESPRIT algorithm[15],the DOA matrix algorithm of Cao[16]and Cramer-Rao bound(CRB).It is indicated in Figs.5–7 that our algorithm has a parameter estimation performance very close to that of the ESPRIT algorithm and the DOA matrix algorithm in a high SNR condition.

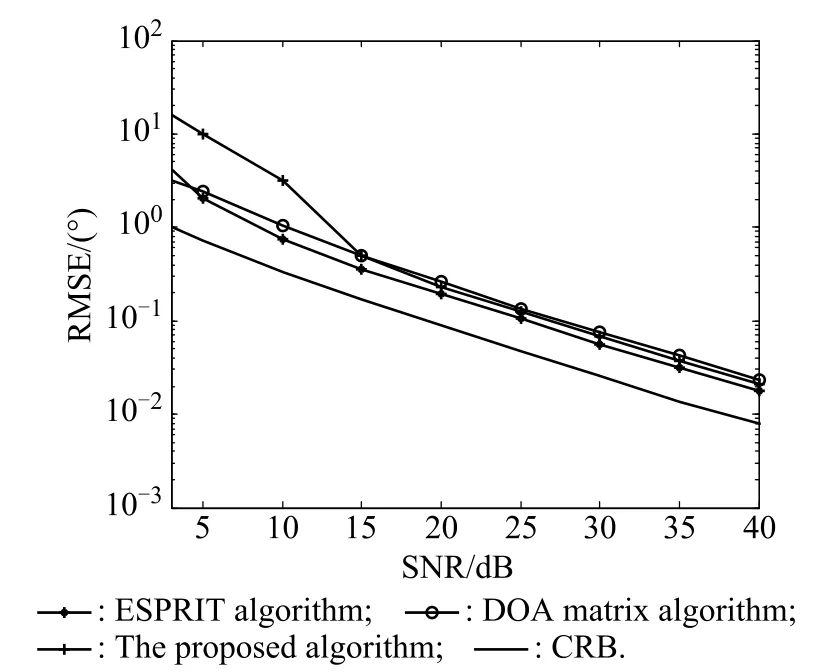
Fig.5 Angle estimation comparison for three targets of the receive array

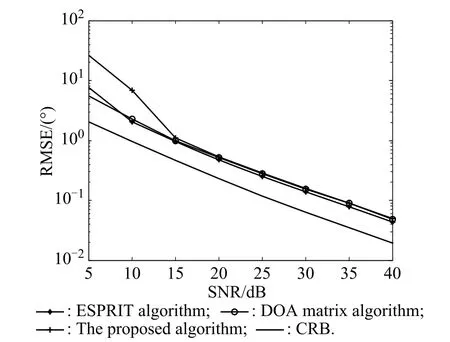
Fig.6 Angle estimation comparison for three targets of the transmit array

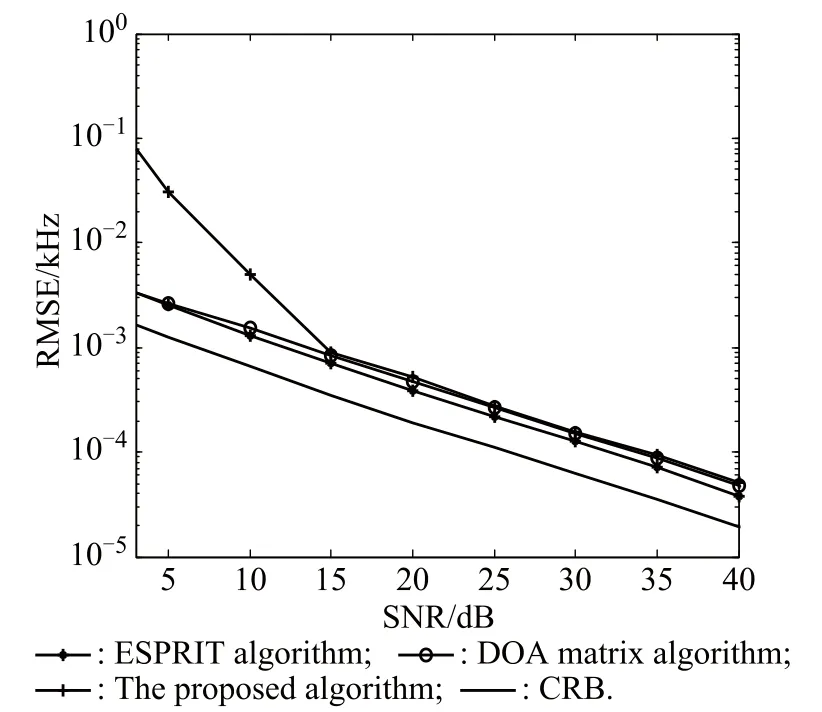
Fig.7 Doppler frequency estimation comparison

Figs.8–10 give parameter estimation performance of our algorithm with M=9,N=9,K=3 and different values of L.It is indicated in Figs.8–10 that the angle estimation performance of our algorithm is improved with L increasing.

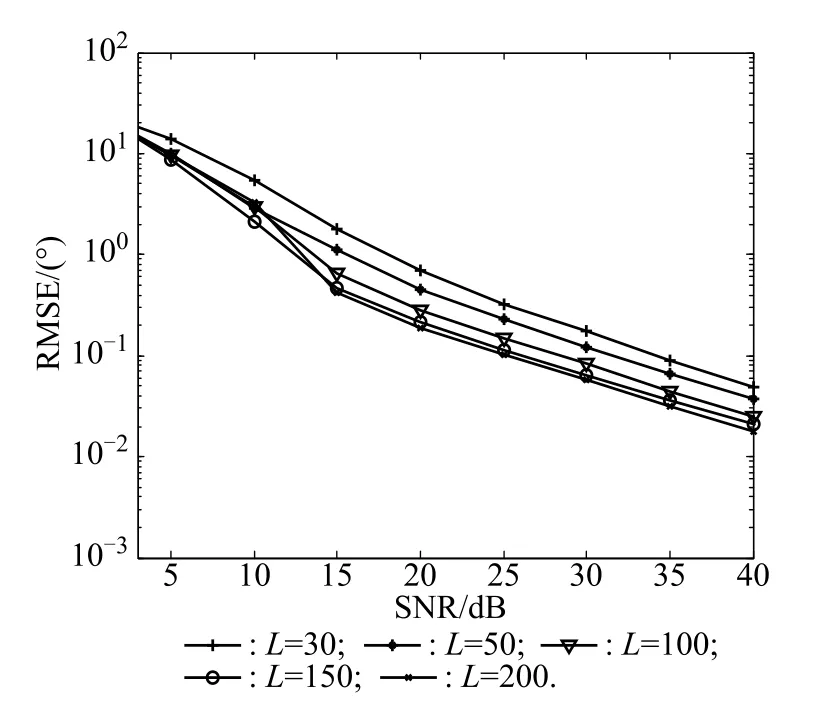
Fig.8 Angle estimation for three targets of the receive array with different values of L

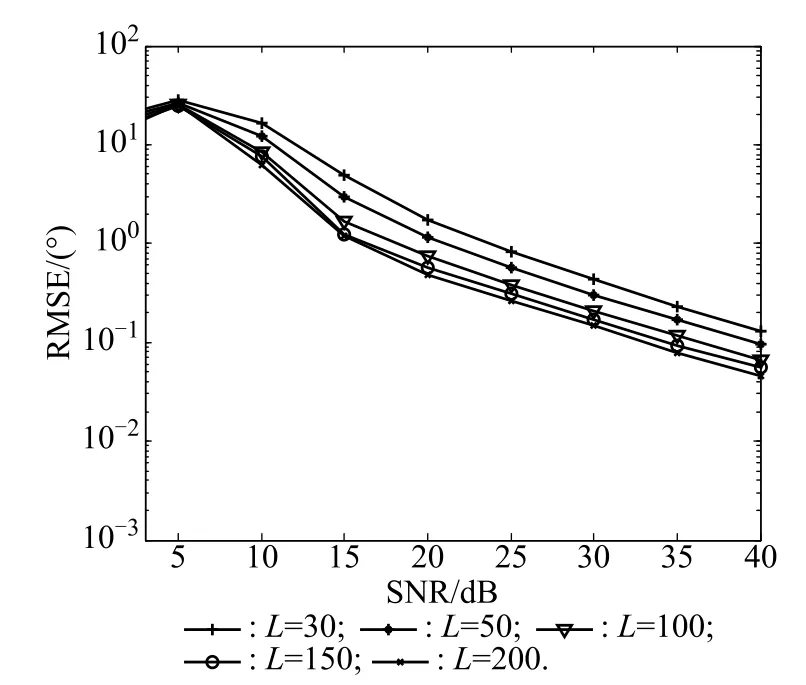
Fig.9 Angle estimation for three targets of the transmit array with different values of L

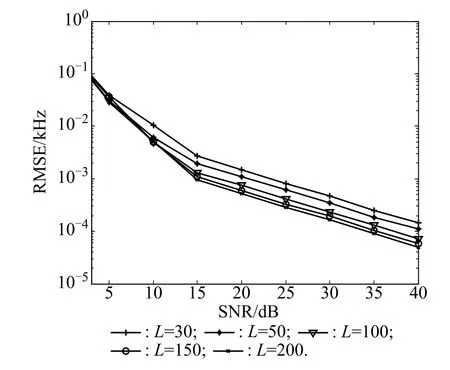
Fig.10 Doppler frequency estimation for three targets with different values of L

5.Conclusions

In this paper we present a low-complexity Doppler frequency,2D-DOD and 2D-DOA estimation for bistatic MIMO radar with arbitrary arrays in spatial colored noise. The proposed algorithm can obtain automatically paired transmit and receive angle estimations and eliminate the spatial colored noise.Then the 3D coordinates of the targets can be obtained from the estimated angle.Furthermore,it provides a lower computational complexity and has parametersestimation veryclose to that of the ESPRIT algorithm and the DOA matrix algorithm in a high SNR. How to improve the parameters estimation performance in a low SNR is the focus of our future work.

[1]E.Fishler,A.Haimovich,R.S.Blum,et al.MIMO radar:an idea whose time has come.Proc.of the IEEE Radar Conference,2004:71–78.

[2]J.Li,P.Stoica.MIMO radar–-diversity means superiority. Proc.of the 14th Adaptive Sensor Array Processing Workshop, 2006:2–6.

[3]E.Fishler,A.Haimovich,R.S.Blum,et al.Spatial diversity in radars models and detection performance.IEEE Trans.on Signal Processing,2006,54(3):823–838.

[4]D.R.Fuhrmann,G.S.Antonio.Transmit beamforming for MIMO radar systems using partial signal correlation.Proc.of the 38th Asilomar Conference on Signals,Systems and Computers,2004:295–299.

[5]L.Xu,J.Li,P.Stoica.Adaptive techniques for MIMO radar. Proc.of the 4th Workshop on Sensor Array and Multichannel Signal Processing,2006:258–262.

[6]J.Li,P.Stoica,L.Xu,et al.On parameter identiability of MIMO radar.IEEE Signal Processing Letters,2007,14(12): 968–971.

[7]L.Xu,J.Li,P.Stoica.Target detection and parameter estimation for MIMO radar systems.IEEE Trans.on Aerospace and Electronic Systems,2008,44(3):927–939.

[8]A.M.Haimovich,R.S.Blum,L.J.Cimini.MIMO radar with widely separated antennas.IEEE Signal Processing Magazine, 2008,25(1):116–129.

[9]X.F.Zhang,D.Z.Xu.Angles estimation in bistatic MIMO radar using improved reduced dimension Capon algorithm. Journal of Systems and Engineering and Electronics,2013, 24(1):84–89.

[10]J.Chen,H.Gu,W.M.Su.Angle estimation using ESPRIT without pairing in MIMO radar.Electronics Letters,2008, 44(24):1422–1423.

[11]X.F.Zhang,L.Y.Xu,L.Xu,et al.Direction of departure and direction of arrival estimation in MIMO radar with reduced dimension MUSIC.IEEE Communications Letters, 2011,14(12):1161–1163.

[12]X.Zhang,Z.Xu,L.Xu,et al.Trilinear decomposition-based transmit angle and receive angle estimation for multiple-input multiple-output radar.IET Radar,Sonar&Navigation,2011, 5(6):626–631.

[13]C.Chen,X.F.Zhang.A low-complexity joint 2D-DOD and 2D-DOA estimation algorithm for MIMO radar with arbitrary arrays.International Journal of Electronics,2013,100(10): 1455–1469.

[14]J.Li,H.Li,B.L.Li,et al.Multiple target three-dimensional coordinate estimation for bistatic MIMO radar with uniform linear receive array.The European Association for Signal Processing(EURASIP)Journal onAdvances inSignal Processing, 2013(81):1–11.

[15]W.B.Fu,T.Su,Y.B.Zhao,et al.Joint estimation of angle and Doppler frequency for bistatic MIMO radar in spatial colored noise based on temporal-spatial structure.Journal of Electronics&Information Technology,2011,33(12):2858–2862.

[16]Y.H.Cao.Joint estimation of angle and Doppler frequency for bistatic MIMO radar.Electronics Letters,2010,46(2):170–172.

[17]J.Li,X.Zhang.Joint estimation of angle and Doppler frequency in bistatic MIMO radar based on quadrilinear decomposition.ActaAeronautica et Astronautica Sinica,2012,33(8): 1474–1482.

[18]L.Y.Xu,G.B.Zhang,X.F.Zhang,et al.Low complexity direction and Doppler frequency estimation for bistatic MIMO radar in spatial colored noise.International Journal of Antennas and Propagation,2014(2014):1–8.

[19]P.Stoica,L.R.Moses.Spectral analysis of signals.New Jersey:Prentice Hall,2005:387–393.

Biographies

Lingyun Xu was born in 1971.She received her M.S.and Ph.D.degrees in information and communication system from Nanjing University of Aeronautics and Astronautics(NUAA)in 2004 and 2012,respectively.Since 2004,she has been a teacher in NUAA and has published more than 20 papers on IEEE journals and conferences and two books.Her research interests are array signal processing,parameter estimation and wireless communication.

E-mail:xlyun@nuaa.edu.cn

Xiaofei Zhang was born in 1977.He received his M.S.and Ph.D.degrees in information and communication system from Nanjing University of Aeronautics and Astronautics(NUAA)in 2002 and 2005, respectively.He is now a professor and Ph.D.supervisor in NUAA.His research interests focus on array signal processing.

E-mail:zhangxiaofei@nuaa.edu.cn

Miao Yu was born in 1975.He received his Ph.D. degree in 2009 from Zhejiang University.Now he is a senior engineer in Nanjing Telecommunication Technology Research Institute.His main researchelds are wireless communication,blind signal processing and antijamming technology.

10.1109/JSEE.2015.00056

Manuscript received March 17,2014.

*Corresponding author.

This work was supported by the National Natural Science Foundation of China(61371169;61179006),the Jiangsu Postdoctoral Research Funding Plan(1301013B),and the Nanjing University of Aeronautics and Astronautics Funding(NZ2013208).