基于分布型电力系统的PSO优化设计
2015-04-11刘凡齐李学生潘俊涛王君瑞
刘凡齐,李学生,潘俊涛,王君瑞
(北方民族大学电气信息工程学院,宁夏银川 750021)
基于分布型电力系统的PSO优化设计
刘凡齐,李学生,潘俊涛,王君瑞
(北方民族大学电气信息工程学院,宁夏银川 750021)
优化了传统粒子群算法,运用了混沌算法对粒子做初始化,优化了传统粒子群算法的收敛特性,并在算法的优化过程中,增加了混沌干扰元素对整体最优化极值做混沌干扰,将符合杂交几率的优化粒子做杂交处理,提高了粒子群的种类,增强了粒子群算法的搜寻水平。并通过IEEE33节点的分布型电力系统做无功优化仿真验证,通过比较,验证了优化算法的优越性与准确性。
电力系统;粒子群;杂交策略;无功补偿;混沌算法
1 混沌算法优化粒子群算法
基于传统粒子群算法初始化步骤为任意选取这一特点,本文拟提出应用混沌算法优化初始化,混沌即利用特定的方程求解出具有混沌特性的变量(混沌变量)。混沌原理的特性如下:混沌变量和随机变量非常接近,体现其任意性;在空间方面,混沌可以设定为无重复经历全部状态的总和;由方程式可得,混沌变量的求解过程是通过特定方程的迭代计算而出的,具有一定的规律性。通过混沌算法改进电力系统无功优化可以实现多方面的改进,如不论无功优化的计算函数连续与否,可以利用混沌算法中,混沌可以设定为无重复经历全部状态的总和这一特征实现非重复性的整体搜索功能。
2 杂交策略
算法优化的中心思想如下:采用混沌干扰因子对粒子群中整体最优位置做扰动处理,依据设定的杂交几率,通过杂交因子对剩余粒子做成对杂交处理,这样有效地增多了粒子群的种类,不仅避免了引起局部最优情况,又提高了具体算法的整体搜寻水平。具体步骤为:在算法的寻优环节中,针对杂交粒子群任意给定某一特定的杂交几率,且粒子群的适应度大小与杂交几率无关,因此每次迭代寻优的过程中,都会根据这一设定的几率去提取定量的粒子做成对杂交处理,杂交结束后,将产生孩子粒子,其数目等同于所提取的杂交粒子个数,为了保持粒子群中粒子数目的恒定性,应将粒子群中做杂交处理的全部粒子都由孩子粒子代替。孩子粒子位置的确定方法是通过父母粒子的具体位置做数学交叉求解得来。
3 基于优化算法的无功优化过程
(1)输入电力系统初始参数,即算法计算需要的原始数据;
(2)统计发电机组在不同阶段的输出功率值;
(3)通过混沌算法对粒子群做初始化;
(4)以给定电力系统为对象,做节点电压及线路功率分布分析,计算所有粒子的适应度值的大小,提取适应度较好的n个粒子作为初始值,随时刷新计算粒子的原始位置与速率,完成对刷新粒子群中整体最优值pg和个体最优值pi的计算;
(5)当符合迭代寻优过程的截止条件时,则结束迭代寻优过程,输出结果;
(6)判定算法状态是否为早熟状态,若算法处于早熟状态则继续,否则跳至步骤(8);
(7)对粒子群所处的最优位置 做混沌优化处理,得到一个混沌变量可行解序列
(9)依据初始化过程中所给定的杂交几率提取余下的粒子群,并对其做成对杂交处理,计算得出孩子粒子,且其个数等同于父母粒子个数,并确定其所处位置与速率;
(10)刷新全部粒子所处位置与速率,返回步骤(4)。
4 算例分析
本文通过建立分布型IEEE33节点电力系统模型,并采用优化的粒子群算法对系统做无功优化,含有分布式电源电力系统简易结构见图1。具体电力系统节点电压的取值范围:[0.95,1.05]。在1号节点处,添加唯一1台有载调压变压器,其共有11个电压分接头,实现可调变比功能。并在系统中10、14、17和31号节点处加装投切并联电容器。其中分布式电源布置在第33号节点上。
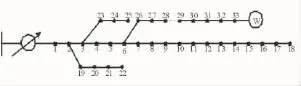
图1 IEEE33节点电力系统
设定发电机组工作条件相同即发电功率一致,表1、表2分别代表传统粒子群算法和整体混沌杂交粒子算法对已建立的分布型IEEE33节点电力系统做无功优化的仿真数据分析。从表中数据可知,利用本文优化的算法对电力系统做无功优化的结果相对于传统粒子群算法而言,其有功网损略有下降,且接入33节点的电压相对于传统粒子去算法的无功优化后的电压较高。
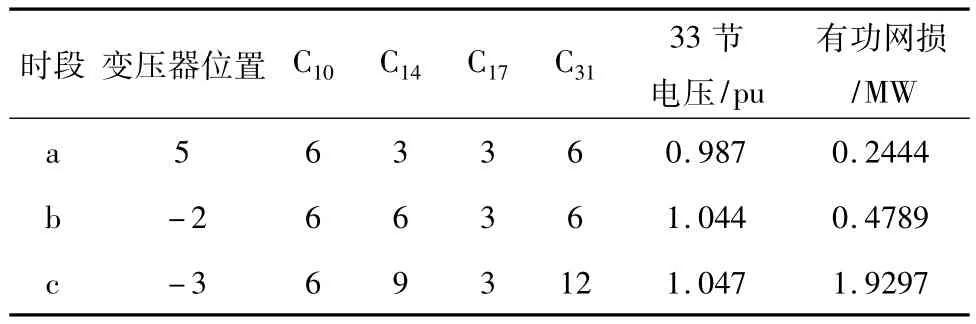
表1 基于粒子群算法的无功优化结果

表2 基于优化算法的无功优化结果
图2是在风速为6m/s情况下,电力系统有功功率损耗在迭代过程中的变化趋势,其中模型为IEEE33节点电力系统,分别应用传统粒子群算法和本文优化算法。从图2可知,采用整体混沌杂交粒子算法相对于传统算法而言,电力系统无功优化有功损耗量较少,说明了改进算法的优越性。
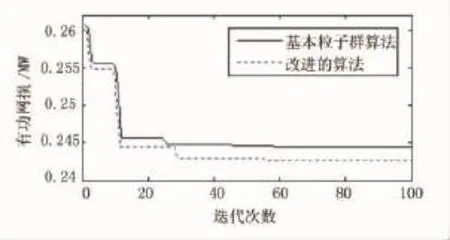
图2 目标函数

图3 风速为6m/s时节点电压

图4 风速为8m/s时节点电压

图5 风速为10.3m/s时节点电压
图3 、图4和图5分别是在不同风速情况下,分布型电源并入配电网前后,线路全部节点的电压情况。发电机组投切无功优化与否并不会产生过多的优势,系统中各节点的电压值都在稳定运行的电压范围内,但含有分布型电源的电力系统运行中,其电压幅值及频率即电能质量具有明显的优越性,其中通过整体混沌杂交算法的电力系统节点电压质量相对更为稳定。从计算结果可知,当风速过大即电机输出功率过大时,不含有分布型电源的电力系统在完成无功优化后,某些节点电压就不在电网正常运行的电压范围之内,严重影响了系统的稳定性与运行安全性,但含有分布型电源的系统运行过程中,节点电压相对稳定,保证了系统的稳定运行。
5 结语
优化了传统粒子群算法,在其中融合了混沌算法与杂交因子理论,利用混沌算法先对粒子做初始化,通过混沌干扰因子对整体最优极值做扰动处理,最后通过杂交因子对满足杂交几率的粒子做杂交处理,通过上述的优化处理,增多了粒子的种类,拓宽了粒子的寻优范围,提高了整体水平。搭建了IEEE33节点的电力系统模型,对传统粒子群算法与优化的算法做仿真比对,由仿真结果可得,优化算法具有较高的鲁棒性,且显著提升了整体寻优水平。
[1]Li T A,Long S C,Feng G.A novel robust adaptive fuzzy track controls for the class of nonlinear systems[J].IEEE Trans on Fuzzy Systems,2010,23(1):124-137.
[2]王施丹,徐力杰,王伟.分布型电力系统无功优化研究方法[J].华北电力大学学报,2012,28(2):41-55.
[3]杨光杰,郑华.分布型电力系统电压无功优化方法的改进与设计[J].现代电力,2012,29(2):45-56.
[4]陈书恒,党小强,李兴媛,等.含有DG装置与设备成本的电力系统无功优化[J].电力系统保护与控制,2012,38(21):37-55.
[5]刘炎华,田茹,张东映,等.风电发电平滑效果的研究[J].电网技术,2012,16(12):2-6.
[6]刘新东,方科,陈焕.利用弃风提高大容量风电消纳能力的浅析[J].电力系统保护与控制,2012,33(6):33-39.
[7]Mates A,Bessar R J.Setting the operae reserves using probabilistic power forecast[J].IEEE Transactions on the Power Systems,2011,526(2):594-601.
[8]Margano E,Faran J,Resande M L,et al.A new controlling strategies the effect compensations for autonomous induction generator speed range turbine[J].Energy Conversions Managements,2013,52(5): 2142-2155.
[9]丁玉凤,文劲宇.基于改进PSO算法的电力系统无功优化研究[J].继电器,2011,33(33):20-24.
[10]Peng,Lei,Zhang Jianping.Reactive power optimization of hybrid AC/HVDC power system based on genetic algorithm and particle swarm optimization[J].Gaodianya Jishu,2012,32(4):78-81.
[11]顾洁,陈章潮,张林.基于遗传算法的无功优化模型研究[J].电力系统及其自动化学报,2011,13(3):10-12.
[12]杨维,李歧强.粒子群优化算法综述[J].中国工程科学,2012,6 (5):87-94.
[13]李爱国,覃征,鲍复民,等.粒子群优化算法[J].计算机工程与应用,2012,38(21):1-3.
[14]谢晓锋,张文俊,杨之廉.微粒群算法综述[J].控制与决策,2013,18(2):129-134.
[15]Shi Y,Eberhart R.C.Empirical study of particle swarm optimization[C].Proceedings of the Congress on Evolutionary Computation.2010.
[16]Ho K L,Hsu Y Y,Yang C C.Short Term load Forecasting Using a Multilayer Neural Network with an Adaptive Learning Algorithm[J].IEEE Trans on Power Systems,2010,7(1):141-149.
[17]Li T S,Tong S C,Feng G.A novel robust adaptive fuzzy tracking control for a class of nonlinear MIMO systems[J].IEEE Trans on Fuzzy Systems,2012,18(1):150-160.
[18]吴汕,梅天华.分布式发电引起的电压波动和闪变[J].能源工程.2011(04):55-60.
[19]Angeline P J.Using selection to improve particle swarm optimization[C].Proceedings of IJCNN,Washington,2010.
[20]Fukuyama Y.Fundamentals of particle swarm techniques,Modern Heuristic Optimization Techniques with Applications to Power Systems[J].IEEE Power Engineering Society,2012.
[21]Eberhart R C,Shi Y H.Particle swarm optimization,developments,applications and resources[M].NJ:IEEE Press,2011.
[22]Chen Yan-qiu,Zhang Yao,Wei Ying-hua.Application of Improved Genetic Algorithm Combining Sensitivity Analysis to Reactive Power Optimization for Power System[C].IEEE Transactions on Restrictions Apply.Nanjing(China):2013.
[23]王世丹,徐丽杰,王 玮.含分布电源的配电系统无功优化研究[J].华北电力大学学报,2012.39(2):39-69.
Design on PSO of distribution network
It use chaos algorithm on the algorithm of the particle in the swarm initializing.The convergence of algorithm is improved.The algorithm add chaotic disturbance fact.In order to chaotic disturbances for the global optimal values,in addition to meet probability of cross the particle hybrid operations,increasing the diversity of particle,improving the global search ability of the PSO algorithm.It introduces the reactive power optimization background,to establish the power web without reactive power optimization models,and carry on the simulation of the IEEE33 system,showing the optimization operations of the distribution work is effective.
power system;PSO;hybrid strategy;reactive power compensation;Chaos algorithm
TM761
B
1674-8069(2015)03-054-03
2015-03-06;
2015-04-20
刘凡齐(1986-),男,硕士,助教,研究方向为电力系统电压稳定性分析。E-mail:liufanqi1986@126.com
国家自然科学基金项目(61463001);宁夏自治区自然科学基金项目(NZ14106)
