把握教材,促进学生有效复习——谈“比和比例的整理与复习”的教学
2015-04-11浙江台州市黄岩区北城街道中心小学318000黄康兵
浙江台州市黄岩区北城街道中心小学(318000) 黄康兵
一、复习中学生出现的一些现象
1.对复习课的学习兴趣不浓
由于教师没有认真备课,对复习课不够重视,照搬教材,认为复习课无非是做做练习再分析,从而导致学生对机械的练习没有兴趣,课堂中也懒得思考,注意力不集中。
2.对概念、公式经常用错
这类学生缺乏知识与技能的整合,没有完全理解所学的概念、公式,平时只是机械地套用公式解题,若题型稍作改变就不知所措。
3.对解决问题只会列式不会说理由
这类学生在平时练习中只会列式解答,如让其口述理由却回答不出来,或对简单的问题能很快解决,但对新课程下丰富、生动、多元的现实问题却束手无策。
4.基础知识没有掌握,学习态度不端正
班级中的后进生虽然心里也很想学习,但由于以前学习的知识没有理解、掌握,体验不到成功的喜悦,久而久之,就形成什么都无所谓、复习不关我的事的态度。
二、有效复习的策略
1.知识的梳理——建立知识结构网络
知识梳理就是让学生回顾基础知识、归纳要点,理清每部分知识的重、难点,全方位的查漏补缺。提高复习课效果的一个主要途径就是在系统原理的指导下,引导学生对所学知识进行系统的整合,从而让学生真正掌握所学知识。
例如,比和比例的横向知识结构。如下图:

比→比的意义→比的基本性质→比的应用↓↓坭坨比例尺按比例分配求比值 化简比 解比例↑比例→比例的意义→比例的基本性质→正(反)比例的意义→比例的应用坭坨图形的放大(缩小)用比例解决问题
在上述比和比例的横向知识结构图中,教师要处理好以下几个问题:第一,比和比例的联系与区别是什么?为什么要引入比?它是在哪些知识的基础上发展的?第二,对练习中的疑难问题怎样去处理?如求比值和化简比的方法容易混淆,怎样把握比例的本质属性?
2.技能的整合——沟通知识间的内在联系
在复习课中,教师不要进行单一的复习,关键要把前后知识串联起来,引导学生综合运用,通过多种方法解决问题。如解应用题时,同一道题,可以看成是归一问题,也可以看成是工程问题,还可以看成是关于比的问题。不同的思路,列式不同,结果相同。这样进行复习,既能给学生以启示,又培养了学生的解题能力。
例如,从比和比例的纵向知识结构网络看,知识点往往是孤立地分阶段进行教学的,所以教师在总复习中必须把它们串联起来,构成一条紧密联系的知识链条。如下图:

同类量的比→知识基础:几分之几(同倍)↓比的意义(比的外部发展)↑不同量的比→知识基础:除法归一、归总应用题 分数(百分数)应用题坼坭比和比例的应用(比的内在演化)
3.变式拓展——促进知识的灵活运用
(1)对生活原型的迁移与同化。
在“比的意义与应用”的复习中,可以选取比的生活知识——按比例分配,引导学生对生活中的知识进行迁移与同化。
①经历配比活动,探索变化规律。
对“牛奶60毫升、糖水15毫升”的饮料配方进行研究,探索如何使饮料口味不变、数量变化时牛奶和糖水共同变化的规律,让学生用翻倍、减半等方法解释饮料口味不变的原因。
②探索配方的多种表示方法,掌握用比表示配方的方法。
讨论:如果有人这样配制饮料,牛奶60毫升,糖水20毫升,口味会相同吗?改变一个数量,能变成4比1吗?在突出用比表示两个同类量之间的关系时,每份所含的具体量必须相同。
③给出具体的数量,要配制1000毫升的饮料,按照4∶1的口味配制,需要牛奶和糖水各多少毫升?现有糖水150毫升,按照4∶1的口味配制,需要牛奶多少毫升?
这样就把比和比例的知识融合在一起,使之形成一个较完整的知识体系,提高了学生对知识的掌握水平。
(2)选取合适的题材。
例如,“已知图形中的线段之比求面积”一直是学生学习平面图形知识的难点,复习中可以从简单的图形到复杂的图形进行拓展,把比例和平面图形面积的计算整合在一起,以此突破这一难点。
①知识再现。
例1.已知两底的关系和同高的图形,求它们面积的关系。
由于正(反)比例的意义比较抽象,学生不易理解,所以他们在具体的应用中是有困难的。因此,可借助图形的演变让学生真正建立起这一概念的本质。如下:
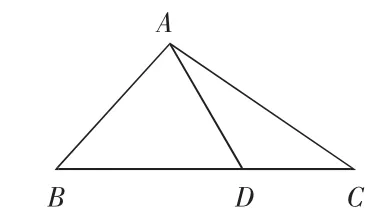
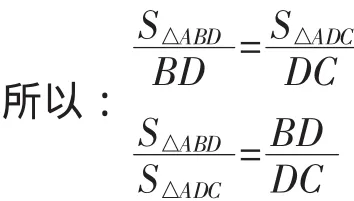
结合具体的图形这一表象,让学生在头脑中建立概念的本质属性:三角形的高一定,面积与底成正比例。也就是说,三角形的高一定,面积之比就是它们的底之比。
②变式拓展。
例2.已知三角形AED的面积是5平方厘米,D是AC的中点,EC与BE的比是1∶3,求三角形ABC的面积?
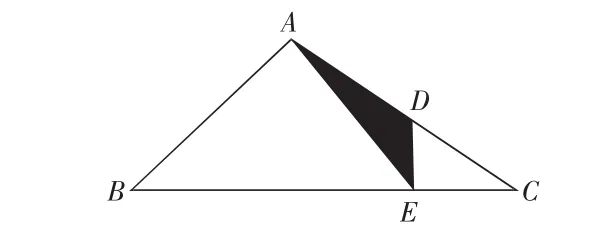
③应用提升。
例3.梯形的上、下底之比是10∶17,已知阴影面积是340平方厘米,求梯形的面积?
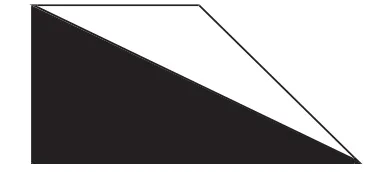
三、有效复习的几点体会
1.通过重复变式得到发展
变式训练有两种类型,即概念性变式和过程性变式。例如,复习“比例的意义”时,如果只是让学生记住比例的定义“表示两个比相等的式子叫做比例”,给出一些具体的概念性变式让学生判断,学生能够判断哪些是比例、哪些不是比例,但这时候学生对比例的理解是浅层次的,并没有真正理解概念的本质。因此,课堂教学中,教师应该采用过程性变式来帮助学生逐步建立比例的意义。过程性变式指用比例表示部分量与整体的关系。如“小明看了一本书的1/4”,看了的页数与总页数的比是 1∶4,写成比例就是“看了的页数∶总页数=1∶4”;剩下的页数与总页数的比是3∶4,写成比例就是“剩下的页数︰总页数=3∶4”。此过程不仅可以帮助学生体验到比与分数之间的关系,而且使学生建立了比例概念的具体模型,为比例的应用打好扎实的基础。
2.通过比较加深对易混淆概念、方法的理解
(1)理解生活中比的意义。
案例:学校购买了一批消毒液,产品的使用说明如下。
①瓜果、餐具、厨房用品 1∶500;
②衣服、用具、家具表面 1∶300;
③染病者的污染物1∶100。
师:说一说各个“比”的现实意义。你会建议学校选择第几种配制方法配制消毒水?
师:这个1∶300表示一份消毒液要加水300份,也就是水的体积是消毒液的300倍,消毒液是水的体积的 1/300。
师:消毒液是配制成的消毒水的1/301,水是配制成的消毒水的300/301。
……
这样教学,运用比较法帮助学生建立认知网络,把比、分数和除法互相转化的思想运用到解决问题之中,能使学生灵活运用所学知识解答有关问题,提高他们的解题能力。
(2)正(反)比例的意义比较。
解答比例关系的应用题(如归一、归总等应用题),可使学生真正认识正比例和反比例的关系。如果只注意正、反比例的概念外延,其实学生还没有真正理解正、反比例的意义。如:“从甲站到乙站,客车行完全程要6小时,货车行完全程要8小时。写出客车与货车所用的时间比与速度比。”时间比:6∶8=3∶4 ,速度比:1/6∶1/8=4∶3。因为路程一定,时间和速度成反比例,所以两个时间比等于相对应的两个速度比的反比。这样进行复习,既引导学生沟通了数学知识间的深层联系,又提高了学生的数学综合能力。
3.通过矫正、分析错例,落实“双基”
纠错教学,是数学教学中不可缺少的一部分。有的学生学习数学感到困难,常常经历失败的打击,很少有成功的体验,导致做题常出错,甚至连自己也不知道是什么原因。要抓好“双基”,首先要关注学生发生错误的现象和成因,切实制定矫正的对策。如在求比值和化简比中,有些学生经常出错,容易混淆,矫正时可让出错的学生明白化简比是把比化成最简单的整数比,比值的意义是比的前项除以比的后项的数值。对于解决问题中思路不清的错误矫正,可先让学生做练习,再让学生陈述解题的思路、过程和依据,还要注重问学生“你是怎样想的”,从而改变以前“不知道理,却会做题”的陋习。其次,学生的错误举不胜举、防不胜防,即使教师反复强调,学生还是反复出错,唯一的办法是提高学生学习数学的兴趣。最后,对集体性的错误整理成学生的错例集,选择适当的时机对这些错误资源加以利用,这对学生掌握基础知识、提高解题能力、完善认知结构有很大的帮助。
