汽轮机扩压调节阀的流体力学研究

崔增娥

（哈尔滨汽轮机厂有限责任公司，哈尔滨 150046）

汽轮机扩压调节阀的流体力学研究

崔增娥

（哈尔滨汽轮机厂有限责任公司，哈尔滨 150046）

对于汽轮机而言调节阀是非常重要的组成部分，文中对扩压调节阀进行详细的流体力学分析研究，得出不同类型扩压调节阀的使用范围。

汽轮机；扩压调节阀；损失系数；提升力

0 引言

汽轮机的启停和变功率是通过调节阀开度的变化，从而改变进入汽轮机的蒸汽流量或蒸汽参数来实现的。作为汽轮机进汽机构的重要组成部分，调节阀气动性能的好坏对整个机组的经济性产生直接影响。另外，调节阀中阀体的振动现象也存在于实际的运行中，曾经发生类似阀杆振动、阀杆断裂、阀座拔起等事故［1－2］，直接影响机组的安全工作。造成阀体振动的主要原因是调节阀内汽流流动的不稳定［3］，而汽流流动的不稳定与流动的边界有密切关系。

因此，无论是从经济性还是安全性来考虑，研究和分析调节阀的内部流场，优化其气动性能，减小流动损失和稳定汽流，提高调节阀的流动效率和安全性，最终设计出汽动性能良好的调节阀具有重要的工程实际意义。

本文将对扩压调节阀的特性进行流体力学研究分析，以便从中掌握其优点和最佳范围。

1 研究方法

本文专门针对有、无扩压器的圆型入口进行流体力学和提升力的研究。

在研究中采用损失系数ζ来表征阻力，

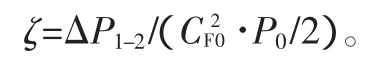
式中：△P1-2为调节阀前后的压力差；CF0为最小截面上的平均速度；P0为调节阀最窄截面上的绝对压力。

这是对于扩压器最小截面而言的，将最小截面上的平均速度CFo=G·vo/Fo，带入上式后得

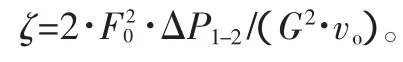
式中：F0为最小截面积；vo为最小截面上的比容；G为流过阀的流量。

当阀门全开时，也就是在扩压器喉部截面上流动速度比较小时若采用ζ的定义，用调节阀前的比容v1代替vo不会产生很大的误差。在没有扩压器的阀中ζ＞1，而在具有扩压器的阀中ζ＜1。所以损失系数必须是对出口截面F2而言的，可以用v1代替调节阀后的比容v2：

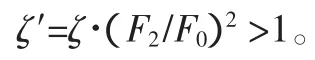
式中：ζ′为对于出口直径而言的损失系数；F2为出口截面积。

损失系数ζ′一方面与构造式样有关，另一方面取决于流动参数（临界马赫数、雷诺数）。

在阀中，提升力是升程的函数，对于任意的升程0≤H≤∞，提升力可以表示为

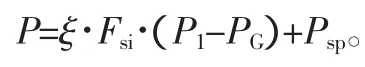
式中：ξ为在确定升程H时的力的系数；Fsi为主阀锥阀座截面积；P1为调节阀前的绝对压力；PG为关闭阀时的绝对出口压力；Psp为阀杆提升力。式中ξ值必须根据试验决定。该方程式对没有卸载和有卸载的阀均可适用。当系数ξ已知时，对于任意大小和几何相似的阀，在任意的阀前压力P1和背阀出口压力PG下，其提升力的变化均可被确定。

没有卸载的阀，当零点升程时ξ=1，在有卸载时，最大提升力产生在中间升程H*时，此时ξmax＜1。（1-ξmax）代表卸载度，用它可以确定在与尺寸相同而没有卸载阀的相反情况下必须使用的最大提升力（在阀杆直径Dsp=0时）。

2 研究描述

2.1 流动研究

本文研究的阀是圆型入口型面轮廓，具有扩压器相对长度（其中LD是扩压管长、D0是最窄直径）LD/D0=0～8，且相应扩压器面积比为F2/F0=1～8，扩压器的扩压角设计成 2θ=6°～14°。雷诺数在 10×105～25×105的范围内不能确定损失系数ζ或者ζ′与雷诺数之间的关系，但可表征临界马赫数的影响。

图1给出了两种不同流入口型面轮廓的损失系数ζ′与临界马赫数之间的关系曲线。在高的临界马赫数范围内可见ζ′的曲线上升。在运行时，马赫数M*a=0.2～0.3，所以在调节阀设计计算时，这种影响不必考虑。

从图1也可以看到流入口轮廓C的损失要小10%左右，但由于它有较大的密封面积，其最大提升力必须增大50%左右。由此估计密闭角小于45°，当密闭角小于45°时，阀杆有卡住的危险。鉴于最大提升力小，因此形式A被认为是最合适的，同时在后面连接一段短的均衡段后可以使气流速度分布均匀地进入扩压器。

图2给出了在不同扩压角下损失系数ζ′与扩压器面积比F2/F0的关系曲线。图中的数值是相应于马赫数M※a=0.25，但对于=0.2～0.3范围内也可以使用，且没有很大的误差。最有利的扩压角是2θ=8°，对于全开的阀所需要的最佳升程值是H/D0=0.33。

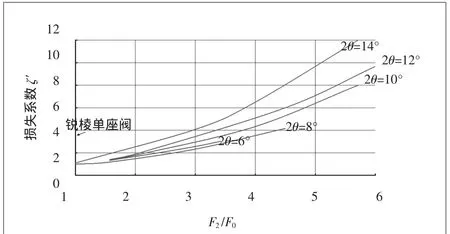
图2 扩压角2θ和面积比F2/F0对损失系数ζ′的影响（=0.25，A的流入口型线）

2.2 力的研究、流量特性曲线

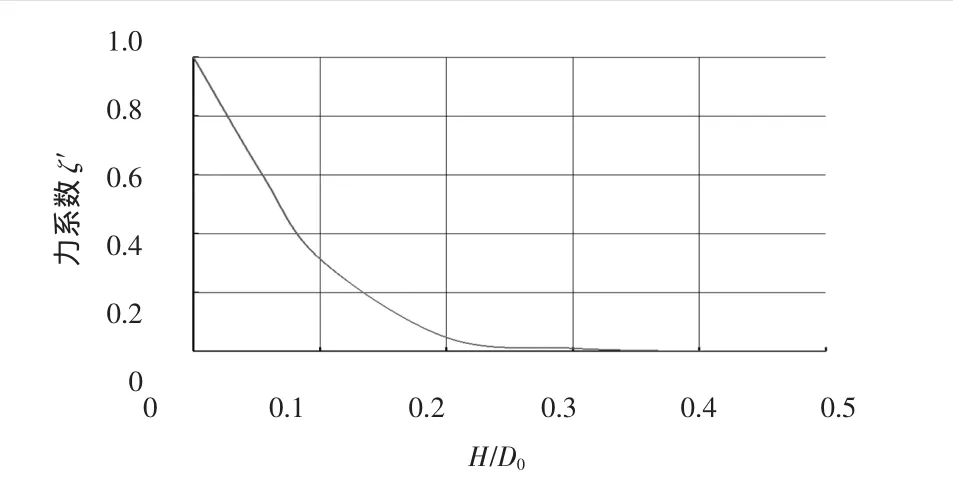
图3 没有卸载扩压阀的力系数ξ变化过程（形式A 的流入口，2θ=12°，F2/F0=2.63，mD=0.43）

力的系数ξ变化过程与比值mD（阀后喷管面积FD与阀的截面积F0之比，即mD=FD/F0）有关。图3给出了没有卸载扩压阀的ξ变化过程，该曲线是在压比P1/PG=10～3和最窄直径P1/PG=10～3和D0=30～60 mm的多次测量中得来的。对于大的mD比值曲线在图示的曲线之上；对于小的mD比值曲线在图示的曲线之下；对于mD=0的，ξ变化过程与坐标轴重合。

图4给出的是具有卸载扩压阀的ξ变化过程曲线。对于H/D=0，ξ0是由预启阀阀座处的截面与主阀阀座截面的比值来确定，即

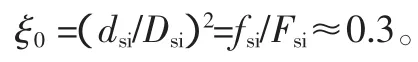
其中：dsi为预启阀锥阀座直径，Dsi为主阀锥阀座直径，Fsi为主阀锥阀座截面积，fsi为预启阀锥阀座截面积。

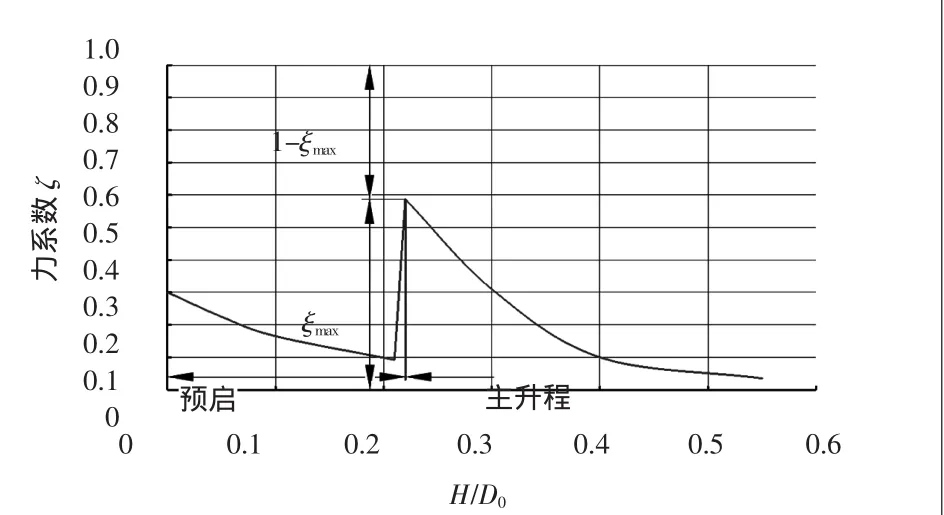
图4 卸载扩压阀的力系数ξ的变化过程（形式A的单流入口，2θ=12°，F2/F0=2.63，mD=0.43）

当阀杆直径很小时，其最大的数值ξmax在H/D=0.22时约为0.6，即卸载系数1-ξmax=40%。

3 结论

1）从流体力学的观点看，最有利的阀是具有圆型流入口轮廓的阀门。

2）最有利的没有卸载扩压阀的是形式A，流入口轮廓扩压角2θ=12°，具有半球形阀锥和面积比F2/F0=1.43～3.77，最大升程 H/D0=0.33。

3）没有卸载的扩压阀较易制造，不需要复杂的进汽室，此外还能保持很好的密封。

4）具有锐棱流入口的阀，由于流体力学和力的不良特性，应该避免采用。

5）在没有卸载的扩压阀上，若最大的力达到不允许的数值，必须采用卸载的扩压阀。

［1］郑绍臣，高福升.汽轮机调速汽门阀杆断裂原因及结构改进［J］.中国电力，1996，29（10）：63-65.

［2］李祥苓，林西奎，寒奎政，等.国产300MW机组高调节汽门阀杆断裂事故分析［J］.中国电力，2002，35（10）：21-24.

［3］毛靖儒，屠删，刘全恩，等.汽轮机调节阀内流动特性的试验研究［J］.工程热物理学报，2002，23（10）：687-690.

（编辑 昊 天）

TK264

B

1002-2333（2015）06-0238-02

崔增娥（1976—），女，工程师，工程硕士，主要研究方向为汽轮机设计及电站系统设计。

2014-10-30