风浪状态对海面粗糙度影响＊

史 剑 蒋国荣

(1.解放军理工大学气象海洋学院 南京 211101;2.解放军理工大学爆炸冲击防灾减灾国家重点实验室 南京 210007)

海面粗糙度是海气界面过程研究的重要参数,准确地估计海面粗糙度对模拟和预报海洋、大气环境要素和现象非常重要。波浪状态对海面粗糙度产生影响,由于测量的局限性,海浪状态对海面粗糙度的影响研究起初在中低风速条件下开展(Guan et al,2004;Shi et al,2011)。目前,运用在海浪数值模式和通量算法中的海面粗糙度均为中等风速条件下得出(Tolman et al,1996;Fairall et al,2003;Smith et al,2014)。Charnock(1955)在空气动力学粗糙度的基础上提出了无量度粗糙度,或称 Charnock数,科学家们经过研究认为 Charnock数与风浪状态有密切的关系,但该类型海面粗糙度考虑风浪状态的参数化方案一直存在争论,Donelan(1990)和 Drennan等(2003)认为Charnock数随波龄的增加而减小,而 Toba等(1990)认为Charnock数随波龄的增加而增大。

此外,采用何种风浪参数对中等风速条件下的海面粗糙度进行参数化也存在一定争议,Masuda等(1987)提出用波龄对无量纲粗糙度进行参数化,Taylor等(2001)提出了一个新的利用波陡参数的无量纲粗糙度参数化方案。最近,Guan等(2004)认为相对波龄、波陡参数能更好地描述中低风速下拖曳系数。Shi等(2011)利用现有实验室和外海测量数据详细分析了各种风浪参数对海面拖曳系数的参数化能力。可见,风浪状态与中等风速下海面粗糙度之间的确存在关系,但其关系的确定性存在争议,特别是采用何种风浪参数还需进一步的研究。

随着风速增加,海面产生飞沫水滴,影响海气界面处各种物理过程(Zhao et al,2006;赵栋梁,2012;史剑等,2013;Soloviev et al,2014)。Powell等(2003)指出海面粗糙度在风速大于 40m/s时粗糙度的值相对Charnock(1955)的值小。Moon等(2007)采用海浪边界层模式来研究台风条件下海浪对海气动量通量的影响,结果表明风速大于30m/s时海面粗糙度的值小于飓风模式中的值。高风速下海浪状态依然影响着海面粗糙度,Shi等(2009)利用新的飞沫生成函数重新计算了海气界面的动量通量,指出在风速大于30m/s时海气之间的动量通量依然受海浪状态的影响。刘斌(2007)推导出高风速下依赖波龄的海面粗糙度参数化方案,并指出 Powell等(2003)和 Donelan等(2004)测量的高风速下海面拖曳系数和粗糙度值相对离散,这主要是风浪引起。因此,在高风速条件下风浪状态对海面粗糙度的影响不可忽视。

1 海面粗糙度参数化方案

1.1 中等风速下海面粗糙度参数化方案

Charnock数为常数意味着海面粗糙度只与风速有关(Charnock,1955),即只考虑了风向海洋中输入能量,而忽略了构成海表面粗糙元的风浪。自由海面风浪的起伏,影响贴近海表面的空气动力场,改变海气界面处的动量通量。因此,不仅海面风速会影响海面粗糙度,风浪状态同样会影响海面粗糙度的大小。

Masuda等(1987)提出了关于Charnock数与波龄关系的一种简单的广义形式,

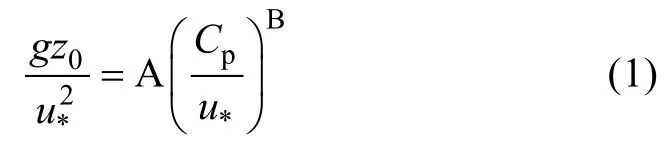
研究者们指出式(1)存在自相关效应(Drennan et al,2003,Shi et al,2011),因为在方程两边均存在摩擦速度u*,并且摩擦速度u*的变化要比Cp的变化快,所以该方程表示的波龄随无量纲粗糙度变化趋势很有可能主要是u*的变化造成的。为了克服这种由于摩擦速度u*产生的缺点,Donelan(1990)提出了一个新的参数-均方根波高σ来无量纲化海面粗糙度,

另有研究者利用有效波高Hs变量来无量纲化海面粗糙度(Drennan et al,2003),

在式(2)和式(3)中,在采用均方根波高和有效波高对海面粗糙度进行无量纲化时,由于波高随着波龄的增加而增加,则无量纲粗糙度必定会随波龄的增加而减小,因此,无量纲海面粗糙度随波龄的变化中波高起到了一定的作用。

Taylor等(2001)提出了一个新的无量纲粗糙度参数化方案,该方案利用波陡进行参数化,

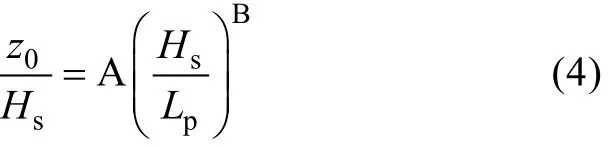
其中,Lp是海浪谱峰对应的波长,为风浪参数波陡,常以δ表示。

式(4)依然利用有效波高对海面粗糙度进行参数化,公式两边均存在有效波高参数,存在自相关效应,也就是说,Taylor等(2001)提出的由波高无量纲化的粗糙度随波陡参数的变化中波高也有贡献。对(2)、(3)和(4)式的分析表明,由波高对粗糙度进行无量纲化均可能存在虚假的自相关效应。

综上所述,风浪状态对海面粗糙度的影响是客观存在的,但无量纲海面粗糙度和风浪参数的参数化关系存在诸多不完善,为避免自相关效应的影响,本文建议海面粗糙度参数化方案采用式(5),

由于式(5)左右两边没有完全相同的参数,以该形式进行海面粗糙度参数化,不存在自相关效应。

1.2 高风速条件下海面粗糙度参数化方案

Makin(2005)给出了适用于高风速条件下的海面粗糙度,

其中 c=gh/ u*2与飞沫层厚度 h有关的参数,可看作无量纲的飞沫层厚度,α为Charnock数,ω为飞沫层中对数风廓线的修正参数,ω =1时说明飞沫对海面粗糙度无影响,ω越小则飞沫层对海面粗糙度的影响越大。将式(5)中 Charnock数代入式(6)中,可以得到考虑波陡影响的海面粗糙度,

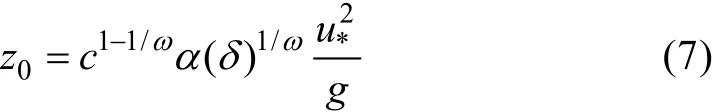
Makin(2005)认为飞沫层厚度 h为有效波高的十分之一,于是,

引入Toba(1972)的3/2指数律关系,

结合式(8)、(9)和(10),得到风浪条件下c与波陡参数之间的关系,

由此,可得到能够适用于高风速条件下的,考虑风浪状态影响的海面粗糙度参数化方案,

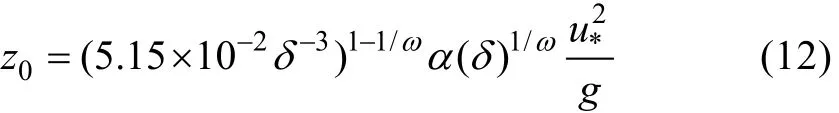
式(12)充分考虑了飞沫悬浮层影响,是式(6)在高风速条件下的应用,下一节中将利用实测数据对式(12)中考虑波陡参数影响的 Charnock数α(δ)进行参数化,并确定ω的取值,从而得到适于高风速条件下的海面粗糙度的具体表达形式。

2 结果与分析

2.1 基于测量测数据参数化海面粗糙度

为了确定(12)式中的α(δ)的具体形式,本文选取实验室和外海测量数据9个数据集进行参数化,来自实验室的数据有Hamada(1963)、Toba(1972)、Kunish(1963)、Kunish等(1966)、Banner等(1998),来自外海观测数据有 Kastaros等(1992)、Geernaert等(1986)、Janssen(1997)、Johnson等(1998)。利用最小二乘法对资料进行分析处理,如图1所示。

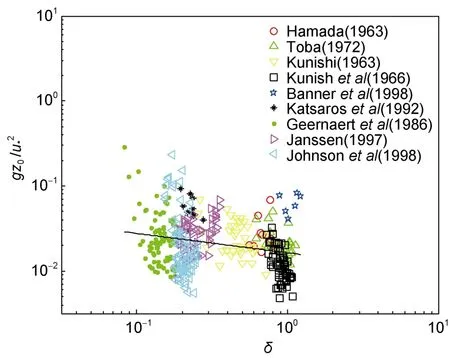
图1 无量纲海面粗糙度 gz0 /u*2与波陡参数δ的关系Fig.1 Relationship between dimensionless sea surface roughness gz0 / u *2 and wave slope parameter δ

经过分析,得到无量纲粗糙度 gz0/u*2与波陡参数δ的参数化关系式为,

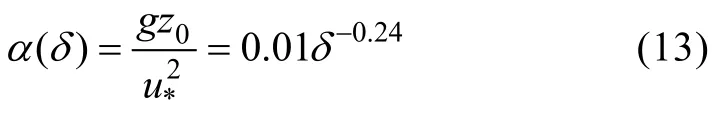
式(13)为中等风速下的无量纲粗糙度参数化方案,由公式可知无量纲海面粗糙度随着波陡的增加而减小,文中将该方案简称为S15M。为了检验S15M参数化方案的准确程度,以下将利用块体算法 COARE(Fairall et al,2003)和FETCH试验数据(Drennan et al,2003)对式(13)计算的摩擦速度进行验证。验证试验中利用 COARE算法中集成的 Taylor等(2001)(简称T01)、Oost等(2002)(简称 O02)提出的两种依赖风浪状态的海面粗糙度参数化方案进行比对,以评估S15M计算海气通量的效果,其中,T01方案具体形式如下,

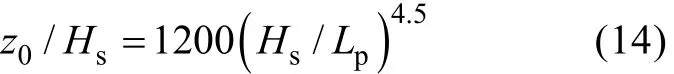
O02方案的具体形式如下:

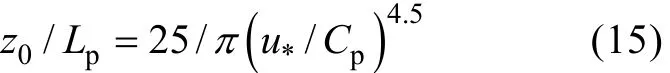
图2显示了COARE算法采用三种无量纲粗糙度参数化方案计算出的海面摩擦速度与测量值的散点对比情况。从图中可初步判断,O02方案计算出的结果与测量结果相差最大,T01和S15接近。

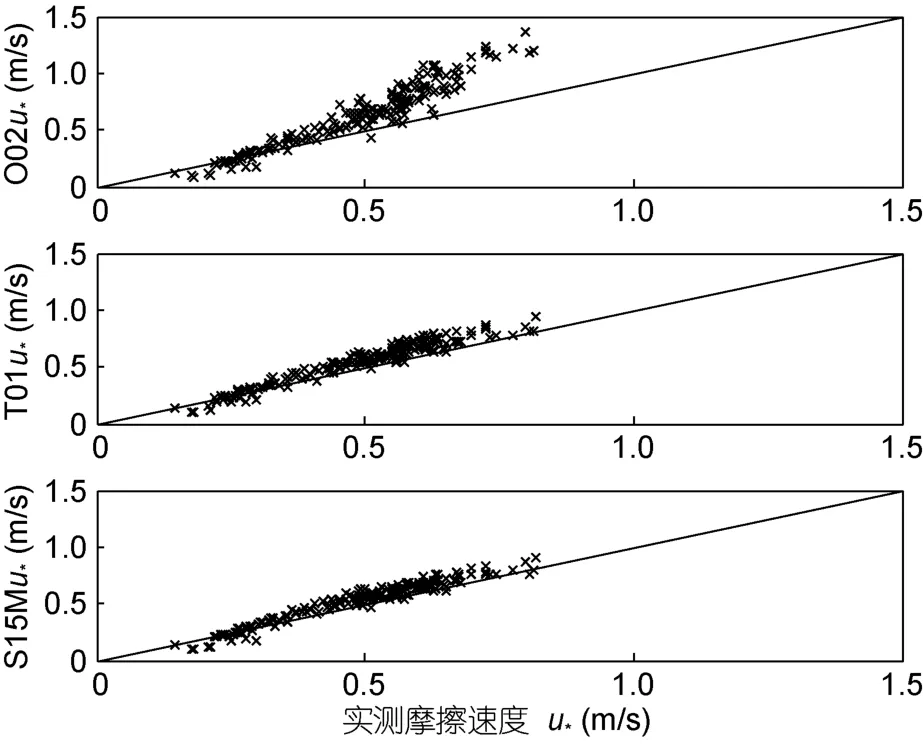
图2 计算出的海面摩擦速度(实线)与测量得到的海面摩擦速度(×号)的对比Fig.2 Calculation (solid line)and observation (symbol ×)of sea surface friction velocity

为了定量分析计算结果的误差,本文选择三个统计误差进行分析,即均方根误差 Root Mean Square Error(RMSE)、平均绝对误差 Mean Absolute Error (MAE)、平均相对误差Mean Relative Error(MRE),以及相关系数Correlation coefficient (CC),如表1所示,RMSE表示为ERMSE,MAE表示为EMAE,MRE表示为EMRE,CC表示为R。

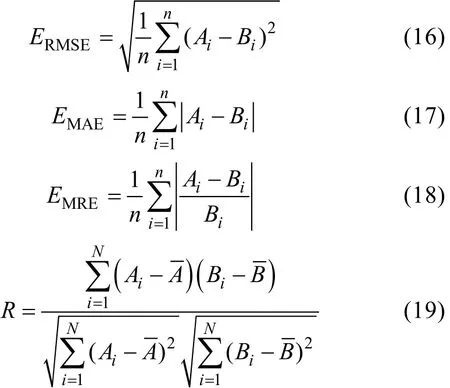
其中,iA是Bi的估计值。

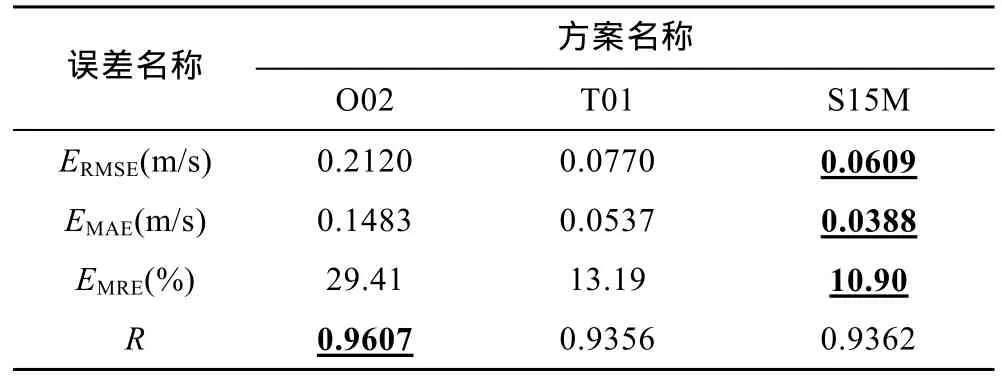
表1 COARE算法采用三种无量纲海面粗糙度方案计算出的海面摩擦速度的误差统计Tab.1 Statistics of error in sea surface roughness friction velocity calculated by COARE algorithm in three dimensionless sea surface roughness schemes

表 1列出三种海面粗糙度计算出的海面摩擦速度值误差,其中下划线表示为三个方案中最优结果。由表可知三种误差S15M方案表现最好,而它的相关系数较 O02方案差,但 O02方案的其他三种误差均最差。因此认为,S15M方案总体上要比COARE算法中的O02和T01更加适合计算海气之间动量通量。

2.2 高风速下海浪状态对海面粗糙度的影响

将参数化得到的式(13)代入式(12),可以得到适用于高风速下的海面粗糙度具体表达形式,

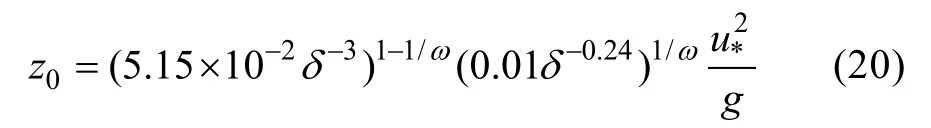
现将式(20)简称为S15H方案,S15H方案充分考虑了波陡对海面粗糙度的影响,其中ω函数来源于Barenblatt(1979)的理论,当风速较高时,海面上方由于飞沫水滴的存在会形成一个飞沫悬浮层,该飞沫悬浮层中的风速分布可表达为,

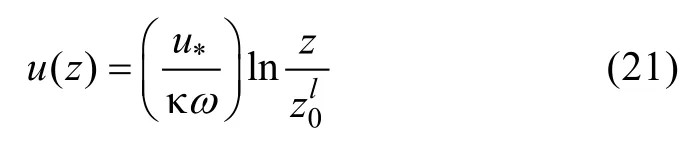
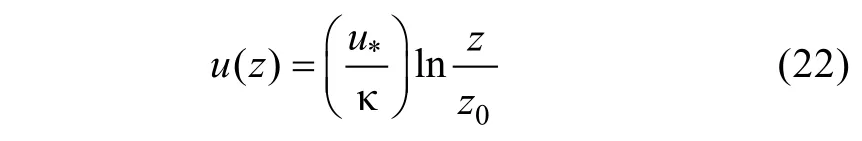
Makin(2005)认为ω= min（1,acr/κu*）,acr是 指在飞沫水滴开始对海面粗糙度产生影响时的飞沫水滴下落末速度,其根据Powell等(2003)的观测数据确定其估计值为 0.64m/s,Makin(2005)认为这是一个貌似合理的值,因为该值对应的仅仅是初始半径为80µm的飞沫水滴。为增强acr取值的理论支撑,本文采用 Andreas(1990)给出的飞沫水滴在接近海面时的下落末速度与飞沫水滴初始半径的关系式(23)计算acr,

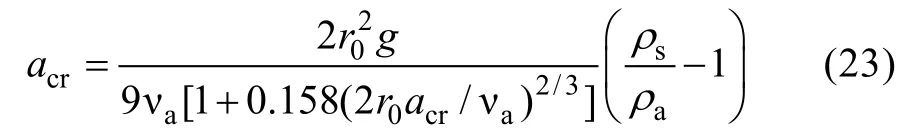
其中,r0是飞沫初始半径,ρs是海水密度,ρa是大气密度,νa=1.5× 10-5m2/s是空气运动学粘性系数。采用牛顿迭代法对水滴接近海面时的下落末速度与水滴初始半径的关系进行计算,当飞沫水滴初始半径为 80µm时,可以得到acr的值为 0.72m/s。由此可以得到S15H方案的完整表达形式。

图3显示了不同波陡条件下海面粗糙度z0随摩擦速度u*的变化情况,图中带有误差条的圆圈数值由Powell等(2003)中的图3a和图3b得来,考虑图3a中风速对应的摩擦速度值误差相对较小,在处理过程中暂不考虑这种误差带来的影响。由图3可知,Makin(2005)提出的粗糙度参数化方案没有考虑风浪状态对海面粗糙度的影响,式(20)在此基础上有了改进,在不同波陡条件下基本能够涉及Powell等(2003)的实测海面粗糙度值的覆盖范围,说明式(20)充分考虑了波浪状态的影响。海面粗糙度在摩擦速度为1.8m/s,对应 Powell等(2003)测量的风速约为 33m/s左右时,之后由于飞沫作用随着风速的增加,导致海面粗糙度开始减小。

值得注意的是,在出现粗糙度最大值之前,若风速确定,海面粗糙度随着波陡的增加而减小;在粗糙度最大值之后,若风速一定,经过一个狭窄的过渡区,海面粗糙度随着波陡增加而增大。由于波陡和波龄存在负相关关系,这一现象也可以用对应的波龄解释。

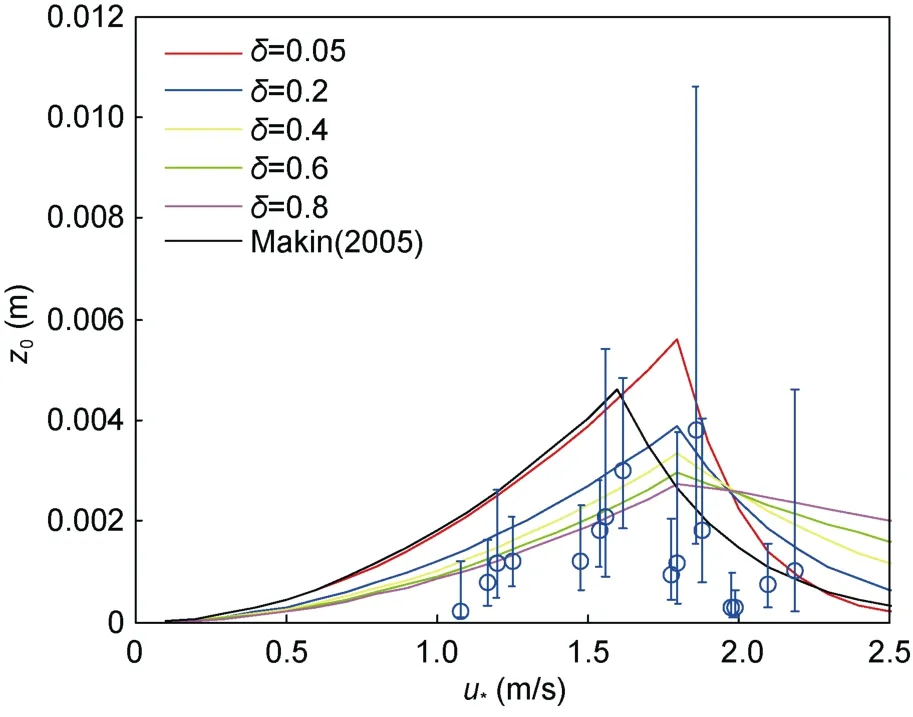
图3 海表面粗糙度与海面摩擦速度的关系。各彩色实线为不同波陡时 S15H方案的值,黑色实线为 Makin(2005)的值,带有误差条的圆圈为 Powell等(2003)测量值Fig.3 Relationship between sea surface roughness and sea surface friction velocity.Color lines represent the S15H results of different wave slopes;black line indicates the roughness in Makin(2005).The cycles with error bar represent the observational data in Powell et al (2003)

2.3 海面粗糙度对台风浪数值模拟影响

为了进一步检验S15H参数化方案的适用性,将该方案加入到海浪数值模式 WAVEWATCH III(Tolman et al,1996)中进行台风浪模拟。选取的个例为2004年的飓风Ivan。Ivan生存时间较长、路径复杂,选取其由南向北经过墨西哥湾的时段进行研究。如图4所示,Ivan在2004年9月14日0时左右进入墨西哥湾,16日8时左右登陆美国。

用以验证模拟的台风浪要素的数据采用美国国家浮标数据中心 National Data Buoy Center(NDBC)提供的浮标资料,由于部分公开的浮标站在2004年9月14日至2004年9月16日期间较多数据缺测,因此仅选取42019、42036、42038、42039四个浮标数据。如图4所示,五角星所示为这 4个浮标的具体位置,它们分布在飓风移动路径的两侧。

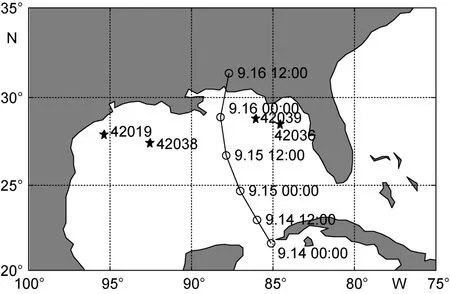
图4 飓风Ivan的移动路径和浮标位置Fig.4 The trajectory of Hurricane Ivan and the buoy (stars)locations

本文采用美国飓风研究部 Hurricane Research Division (HRD)热带气旋观测系统的高分辨率风场,该风场时间分辨率为3—6h,空间分辨率为6km×6km,该数据已被Moon等(2007)、Fan等(2009)证明该台风风场不存在被低估的现象,但该风场数据覆盖的范围仅为围绕台风中心8°×8°。为了充分考虑外围风场产生的海浪的影响,外围风场采用 QSCAT/NCEP混合风场,该混合风场空间分辨率为0.5°×0.5°,时间间隔为 6h,覆盖了 0º—360°E、88°S—88°N 的范围。将这两个组合的风场在时、空上进行插值(Fan et al,2009),构建时间分辨率为 15min的混合风场,以驱动海浪模式模拟台风浪。文中具体的试验方案设计如表2所示,其中T96方案为WAVEWATCH III模式中默认方案,M05方案为 Makin(2005)提出的粗糙度参数化方案。

表2 试验方案Tab.2 Experimental designs

HRD热带气旋观测系统提供的Ivan飓风高分辨率风场资料的时间范围是2004年9月14日21时至16日15时。由于时间较短,文中利用2004年9月13日0时至14日21时的QSCAT/NCEP混合风场启动模式。

表3中,有下划线的数据表示为三个试验中最优结果。由表可知,试验EXP2中的各种误差值与试验EXP3的较接近,但各种误差的最优值在试验 EXP2中最多,表明相对其他 2个海面粗糙度方案,试验EXP2中的S15H海面粗糙度参数化方案能够较好地模拟飓风 Ivan的台风浪有效波高,同时说明在模拟台风浪时应尽量采用考虑风浪状态影响的海面粗糙度方案。

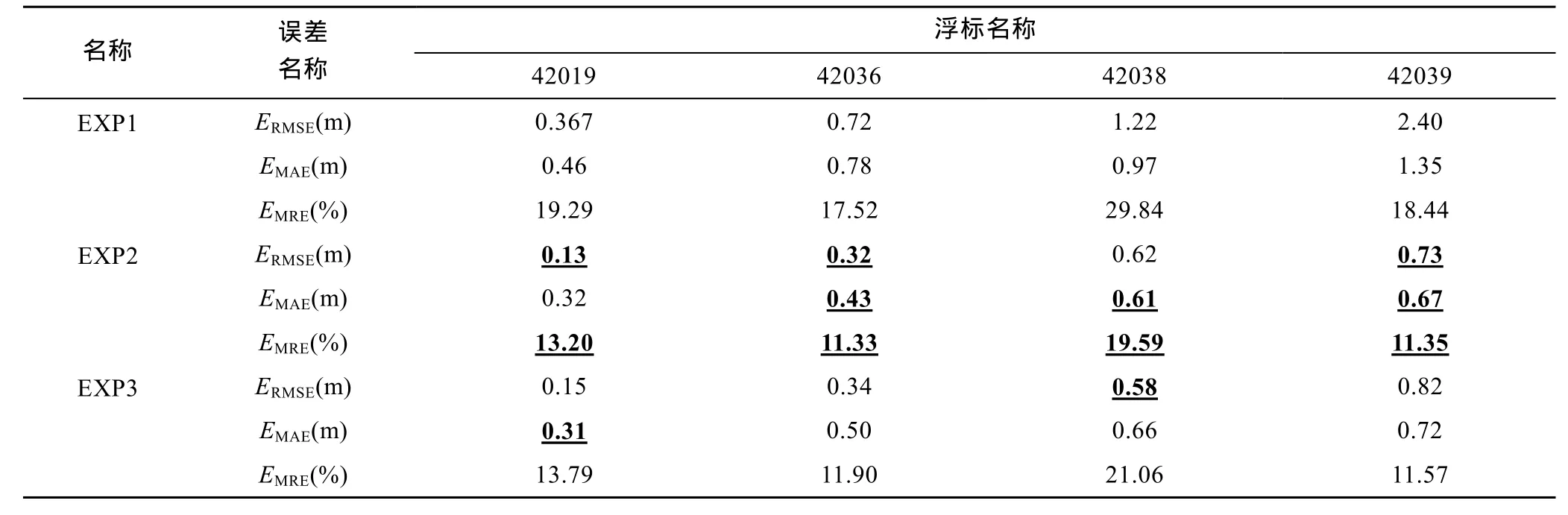
表3 EXP1至EXP3试验模拟出的有效波高值误差统计Tab.3 Statistics of error in significant wave height simulated in experiments EXP1 to EXP3

3 讨论

考虑海面粗糙度与海面拖曳系数Cd存在一一对应的关系(Makin,2005),

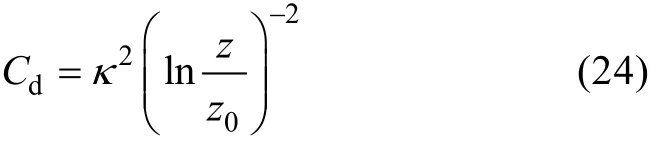
因此,基于式(24)可将海面粗糙度转化为海面拖曳系数,通过分析海面拖曳系数随风速的变化,进一步确认本文提出的海面粗糙度参数化方案的合理性。图5所示为由式(24)计算出的不同波陡条件下海面拖曳系数随风速的变化关系。

不同条件下测量的海面拖曳系数存在一定程度的离散,由图5可知,式(24)在不同波陡条件下均能够涉及这些离散点,说明波浪状态对海面拖曳系数存在影响,且在风速达到30—40m/s时海面拖曳系数发生衰减,该结论与Powell等(2003)相似。波浪状态与海面拖曳系数的关系在图5中与图3类似,即当风速小于40m/s时,海面拖曳系数随波陡参数增大而减少,当风速大于40m/s时海面拖曳系数随波陡参数增大而增大,说明波浪状态与海面粗糙度或拖曳系数的关系随着风速增加会发生变化,产生这一现象主要原因是由于当风速达到一定值时,波浪破碎产生飞沫水滴的作用明显增强,并且飞沫水滴随波龄增加,抑制了波浪对海面粗糙度或海面拖曳系数的影响,最终使得海面粗糙度或海面拖曳系数随波龄的增加而减小(史剑等,2013),对应为海面粗糙度或海面拖曳系数随波陡的增加而增大。

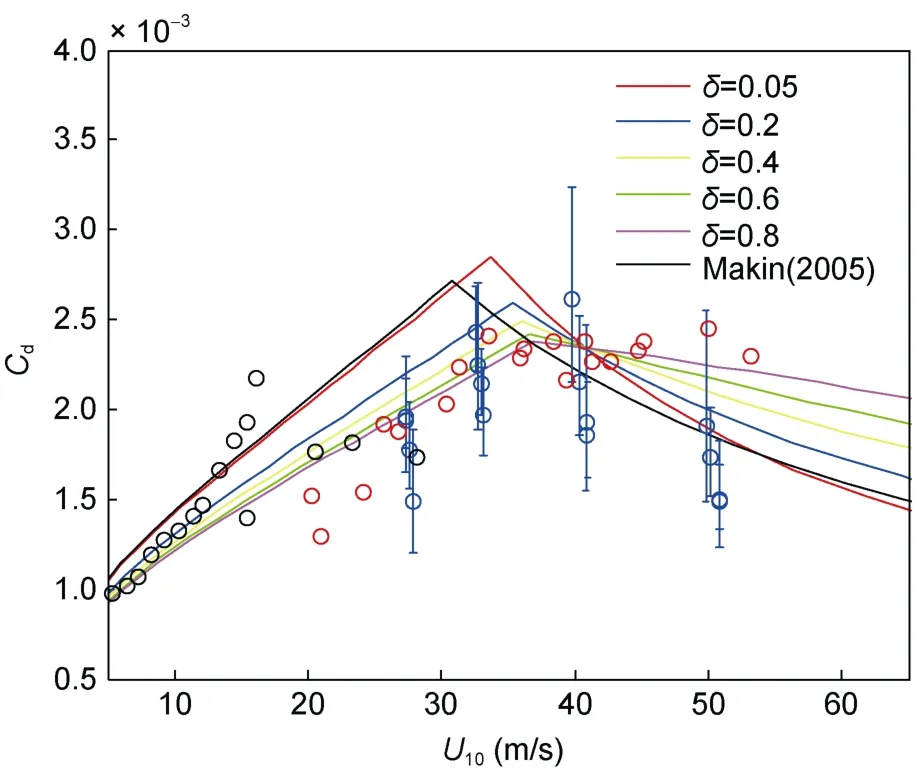
图5 海表面拖曳系数与风速的关系彩色实线为不同波陡时S15H方案的值,黑色色实线为Makin(2005)的值,带有误差条的蓝色圆圈为 Powell等(2003)测量值,红色圆圈为Donelan等(2004)测量值,黑色圆圈为Black等(2007)测量值Fig.5 Relationship between sea surface drag coefficient and wind speedColor lines represent the S15H results of different wave slopes.The black line is the roughness in Makin (2005).Blue cycles with error bar indicate the observation of Powell et al (2003),red ones for Donelan et al (2004),and black ones for Black et al (2007)

4 结论

本文通过理论分析,发现采用波陡参数对海面粗糙度参数化能够有效避免自相关现象,并基于外海和实验室测量数据,得到了中等风速条件下的无量纲海面粗糙度与波陡的关系式S15M。利用块体算法COARE和FETCH试验数据对S15M方案进行验证,结果显示该方案计算海面摩擦速度较块体算法COARE默认的两个依赖波浪状态的海面粗糙度参数化方案更好,说明S15M方案能够很好地计算出中等风速条件下海气界面的动量通量。

在中等风速下海面粗糙度关系式 S15M 的基础上,考虑飞沫悬浮层的影响,建立了适用于高风速条件下的海面粗糙度参数化方案 S15H,该粗糙度方案同样采用波陡参数进行参数化,基于此考虑了风浪状态的影响。文中分析了S15H在不同波陡条件下海面粗糙度随摩擦速度变化的规律,以及由S15H得到的海面拖曳系数随风速的变化规律,发现在未出现飞沫时,海面粗糙度随着波陡的增大而减小,但当出现飞沫后,海面粗糙度逐渐随着波陡增大而增大。将理论值与测量数据进行比对,发现S15H方案相对于经典的海面粗糙度 M05方案有了明显改进,计算值随着波陡的变化基本涉及测量值覆盖范围,说明高风速条件下海面粗糙度需要考虑风浪状态的影响。将S15H方案加入WAVEWATCH模式中,模拟Ivan飓风产生的台风浪有效波高,结果较采用海浪模式默认方案和M05方案更接近测量值,说明将S15H方案运用到海浪模式中进行台风浪模拟具有一定的可靠性。

史 剑,周 林,杨隆颖,2013.高风速下海洋飞沫水滴对拖曳系数的影响.物理学报,62(3): 39201

刘 斌,2007.大气-海浪耦合模式的物理基础及数值研究.青岛: 中国海洋大学博士学位论文,27—29

赵栋梁,2012.海洋飞沫及其对海-气相互作用影响的研究进展.地球科学进展,27(6): 624—632

Andreas E L,1990.Time constants for the evolution of Sea spray droplets.Tellus,42(5),doi: 10.1034/j.1600-0889.1990.t01-3-00007.x

Banner M L,Peirson W L,1998.Tangential stress beneath wind-driven air-water interfaces.J Fluid Mech,364,115—145

Barenblatt G I,1979.Similarity,Self-Similarity and Intermediate Asymptotics.New York,USA: Consultants Bureau Press,218

Black P G,D’Asaro E A,Sanford T B et al,2007.Air-Sea exchange in hurricanes: synthesis of observations from the coupled boundary layer air-Sea transfer experiment.Bull Amer Meteor Soc,88(3): 357—374

Charnock H,1955.Wind stress on a water surface.Quart J Roy Meteor Soc,81(350): 639—640

Donelan M A,1990.Air-Sea interaction.In: Le Mehaute B,Hanes D M eds.The Sea: Ocean Engineering Science.New York,USA: Wiley-Interscience Press,239—292

Donelan M A,Haus B K,Reul N et al,2004.On the limiting aerodynamic roughness of the ocean in very strong winds.Geophys Res Lett,31(18): L18306

Drennan W M,Graber H C,Hauser D et al,2003.On the wave age dependence of wind stress over pure wind seas.J Geophys Res,108(C3): 8062

Fairall C W,Bradley E F,Hare J E et al,2003.Bulk parameterization of air-Sea fluxes: updates and verification for the COARE algorithm.J Climate,16(4): 571—591

Fan Y L,Ginis I,Hara T et al,2009.Numerical simulations and observations of surface wave fields under an extreme tropical cyclone.J Phys Oceanogr,39(9): 2097—2116

Geernaert G L,Katsaros K B,Richter K,1986.Variation of the drag coefficient and its dependence on Sea state.J Geophys Res,91(C6): 7667—7679

Guan C L,Xie L,2004.On the linear parameterization of drag coefficient over Sea surface.J Phys Oceanogr,34(12):2847—2851

Hamada T,1963.An experimental study of development of wind waves.Rep Port Harbour Tech Res Inst,2: 1—41

Janssen J A M,1997.Does wind stress depend on Sea-state or not?-a statistical error analysis of HEXMAX data.Boundary-Layer Meteorol,83(3): 479—503

Johnson H K,Højstrup J,Vested H J et al,1998.On the dependence of Sea surface roughness on wind waves.J Phys Oceanogr,28(9): 1702—1716

Katsaros K B,Atakturk S S,1992.Dependence of wave breaking statistics on wind stress and wave development.In: Banner M L,Grimshaw R H J eds.Breaking Waves,Proc.IUTAM Symposium.Sydney,Australia: Springer-Verlag Press,119—132

Kunish H,1963.An experimental study on the generation and growth of wind waves.Bull Disas Prev Res Inst Kyoto Univ,61: 1—41

Kunish H,Imasato N,1966.On the growth of wind waves by high-speed wind flume.Bull Disas Prev Res Inst.Kyoto Univ,Annals,9: 1—10

Makin V K,2005.A note on the drag of the Sea surface at hurricane winds.Boundary-Layer Meteorol,115(1):169—176

Masuda A,Kusaba T,1987.On the local equilibrium of winds and wind-waves in relation to surface drag.J Oceanogr Soc Japan,43(1): 28—36

Moon I-J,Ginis I,Hara T et al,2007.A physics-based parameterization of air–Sea momentum flux at high wind speeds and its impact on hurricane intensity predictions.Mon Wea Rev,135(8): 2869—2878

Oost W A,Komen G J,Jacobs C M J et al,2002.New evidence for a relation between wind stress and wave age from measurements during ASGAMAGE.Boundary-Layer Meteorol,103(3): 409—438

Powell M D,Vickery P J,Reinhold T A,2003.Reduced drag coefficient for high wind speeds in tropical cyclones.Nature,422(6929): 279—283

Shi J,Zhao D L,Li X Q et al,2009.New wave-dependent formulae for Sea spray flux at air-Sea interface.J Hydrodyn,21(4): 573—581

Shi J,Zhong Z,Li R J et al,2011.Dependence of Sea surface drag coefficient on wind-wave parameters.Acta Oceanol Sin,30(2): 14—24

Smith R K,Montgomery M T,Thomsen G L,2014.Sensitivity of tropical-cyclone models to the surface drag coefficient in different boundary-layer schemes.Quart J Roy Meteor Soc,140(680): 792—804

Soloviev A V,Lukas R,Donelan M A et al,2014.The air-Sea interface and surface stress under tropical cyclones.Sci Rep,4: 5306,doi: 10.1038/srep05306

Taylor P K,Yelland M J,2001.The dependence of Sea surface roughness on the height and steepness of the waves.J Phys Oceanogr,31(2): 572—590

Toba Y,1972.Local balance in the air-Sea boundary processes: I.on the growth process of wind waves.J Oceanogr Soc Japan,28(3): 109—120

Toba Y,Iida N,Kawamura H et al,1990.The wave dependence of sea-surface wind stress.J Phys Oceanogr,20(5): 705—721

Tolman H L,Chalikov D,1996.Source terms in a thirdgeneration wind wave model.J Phys Oceanogr,26(11):2497—2518

Zhao D L,Toba Y,Sugioka K-I et al,2006.New Sea spray generation function for spume droplets.J Geophys Res,111(C2): C02007,http: //onlinelibrary.wiley.com/doi/10.1029/2005JC002960/pdf