影响坦帕湾水交换的三种因素*

朱　君　韩树宗　郑连远

(1. 中国海洋大学海洋环境学院　青岛　266100;2. College of Marine Science, University of South Florida, St Petersburg, FL 33701, USA)

海湾和河口通常是人类海洋活动(如港口码头、海水养殖等)的聚集区, 其沿岸排放的生活污水以及河流携带的污染物、营养盐等也都在此汇集。这造成了海湾和河口脆弱的生态环境(褚芹芹等, 2010), 使得它们成为海洋生态灾害频繁暴发的地区之一。海湾和河口的水交换是指其内部水污染物通过对流和扩散过程与周围海水进行混合, 其浓度降低, 水质得到改善的过程。水交换能力的强弱反映了水体自身的净化能力, 对水体的污染程度(Havenset al, 2010)、浮游植物和鱼卵的分布(Basuetal, 1996)等现象的分析和预测具有重要意义。衡量水交换能力的依据有很多,如水体滞留时间、水体年龄和半交换期等, 本文主要通过水体的滞留时间来进行相关研究。

对海湾和河口内水体滞留时间的研究有很多,起初一些研究学者利用湾口的潮通量进行估算, 如Ketchum 等(1951)、Zimmerman(1988)以及 Sanford 等(1992)。后来, 一些学者依据淡水排放速率进行估算,如 Dyer(1973)、Officer(1980)、Miller等(1991)、Hagy等(2000)以及 Huang等(2002)。这些方法通常是基于箱式模型, 将整个海湾或河口作为一个整体或拆分为几个部分进行研究, 因而无法准确描述海水滞留时间在空间分布的差异性。Oliveira等(1997)、Monsen等(2002)、Sheldon等(2002)和 Aikman 等(2005)对这些方法分别进行了详细的评述。随着高性能计算机的出现, 数值模型被广泛地应用在海水滞留时间的计算上。目前, 通过数值模型计算海水滞留时间主要有两种方法, 一种是使用拉格朗日粒子追踪方法模拟追踪虚拟粒子(Burwelletal, 2000; Monsenetal, 2002;Meyersetal, 2008; 王聪等, 2008), 另一种是通过欧拉弥散模型模拟示踪物浓度的对流扩散(Burwelletal,2000; Yuanetal, 2007; Aregaetal, 2008; Warneretal,2010; Zhangetal, 2010)。对于这两种方法, 滞留时间通常定义为拉格朗日粒子数或物质浓度降为初始粒子数或初始浓度的1/e(0.37)所用的时间。相对于拉格朗日粒子追踪模型, 欧拉弥散模型在考虑对流的同时, 还考虑了浓度的扩散过程。除此之外, 拉格朗日粒子追踪方法在数值模型实现时对随机游走的参数化以及被追踪粒子进出开边界的处理上都较为困难。综合考虑以上因素, 本文采用欧拉弥散模型来计算滞留时间。

1　研究区域

坦帕湾是美国佛罗里达州水域面积最大的河口,同时也是佛罗里达州最大的深水港口之一, 它位于美国佛罗里达州中部, 西侧与墨西哥湾相邻(图1)。整个坦帕湾由四个部分组成: Old Tampa Bay,Hillsborough Bay, MiddleBay和 Lower Tampa Bay。坦帕湾的湾口至湾顶的长度约为 56km, 宽度约为8—16km。坦帕湾水深较浅, 基于面积权重的平均水深约为 4m, 航道处平均水深约为 12m, 但在湾口最大水深可达 25m(图2)。坦帕湾的主航道呈东北西南向, 从坦帕湾湾口的Egmont Key一直延伸到Hillsborough Bay。坦帕湾表面积约为1030km2, 流域面积约为 4600km2, 水体总体积约为 4×109m3。流入坦帕湾的河流较多, 年平均河流入水量约为 63m3/s,主要包括 Hillsborough(15m3/s), Alafia(13m3/s), Manatee(10m3/s)和Little Manatee(6m3/s)四条河流(Lewisetal,1988)。

图1　坦帕湾位置图Fig.1　Geographic location of the Tampa Bay

图2　坦帕湾水深图Fig.2　The bathymetry of the Tampa Bay

坦帕湾水交换的研究始于 Goodwin(1987), 该研究因为采用了深度平均密度定常的正压模型, 所以无法模拟河口中对水交换起重要作用的重力环流,因此该研究无法准确估算坦帕湾跟其邻近海域的水交换。之后, Burwell等(2000)采用三维模型, 利用拉格朗日粒子追踪方法和欧拉弥散模型对坦帕湾的水交换进行了分析。但是, 他们的模型存在两个缺点: (1)开边界设在坦帕湾湾口, 一旦粒子通过开边界离开计算区域后就不能继续进行追踪, 但事实上, 部分离开的粒子在潮汐作用下仍有可能返回模型计算区域;(2)模型网格水平分辨率较低, 很多重要的物质输运通道没有包括在内。因此, 他们同样无法对坦帕湾的滞留时间进行准确估算。为了克服上述缺点, Weisberg等(2006)采用有限体积近岸海洋模式 FVCOM, 对坦帕湾和邻近的墨西哥湾进行了模拟, 但仅采用箱式模型估算了坦帕湾的平均滞留时间。随后, Meyers等(2008)对坦帕湾的水交换进行了较为详细的分析, 但因为采用了和 Burwell等(2000)相同的坦帕湾数值模型, 所以也无法对坦帕湾的水交换能力给出客观的评价。

基于目前坦帕湾水交换的研究现状, 本文设定了两个主要研究目标: (1)以 2001年秋季为例, 通过建立的包含坦帕湾重要物质输运通道的高分辨率数值模型来研究坦帕湾水交换能力的空间分布特征;(2)通过实验对比研究潮汐、河流和风对坦帕湾海水滞留时间的影响及其影响机理。

2　模型实现

本文数值模拟采用的是有限体积方法、非结构网格和基于原始方程的近岸海洋模式 FVCOM(Chenet al, 2003)。模型设计区域包括整个坦帕湾, 以及相邻的河流、水道和 Sarasota Bay, 同时为了包括墨西哥湾和坦帕湾的相互作用, 模型计算区域也包含了一部分陆架(图3)。模型开边界距离坦帕湾湾口约50km。模型水平分辨率在开边界约为 8.5km, 至近岸区域约增加为 200m, 在坦帕湾内部, 模型分辨率进一步提高并在航道、河道、桥洞以及相邻的水道提高到约20m。这是目前坦帕湾分辨率最高的数值模型。该模型水平方向共有219337个三角单元, 115369个节点, 垂直方向采用σ坐标, 等分为11层。基于数值模型计算的 Courant-Friedrichs-Levy稳定条件, 内外模时间步长分别设为1.2秒和0.3秒。模型计算起止时间分别为2001年8月24日0时和 2001年11月30日24时, 总计99天。前8天为模型调整时间, 利用后91天模拟结果分析2001年秋季相关实验下滞留时间的分布情况。

图3　模型网格图Fig.3　Model grid and zoomed views in this study

数值模型采用 NOAA/USGS的水深数据(Hess,2001), 数据空间分辨率为30m。模型开边界水位强迫包含两个部分, 一是潮汐引起的水位变化, 一是气象条件(主要为风场)引起的水位变化。潮汐引起的水位变化包含了主要的半日分潮M2、S2、N2和K2以及主要的全日分潮O1、K1、P1和Q1, 这些分潮数据来自于分辨率为 1/45°的墨西哥湾 OTPS潮汐模型(Egbertet al, 2002)。气象条件引起的水位变化除了包括计算区域内风场的直接作用之外, 同时考虑了模拟区域外风场的贡献。区域外风场对开边界水位的影响采用的是基于坦帕湾外海十年风场和水位观测资料的统计经验关系(Weisberget al, 2006)。模型初始水位和初始流速设为零。初始温度场空间一致, 为20°C。初始盐度场由分辨率较低的大区网格(Zhenget al, 2012)插值而来, 这里使用的是垂向均匀的初始盐度场。模型的具体配置, 包括模型开边界条件、初始条件、水深数据、河流流量、气象强迫条件, 以及模型的详细验证过程, 包括与实测水位和流速以及与前人的研究成果(Weisbergetal, 2006) 的对比情况, 请参见Zhu等(2014a)。Zhu等(2014b)同时利用该模型分析了口门之间的潮流相位差对水交换的作用, 航道加深加宽对水交换的影响以及双指数曲线拟合方法在估算滞留时间上的应用。

本文示踪物的模拟使用的是 FVCOM 中的示踪模块(Chenetal, 2004; Chenetal, 2008)。该模块主要用以模拟保守物质的对流和扩散, 其数值计算方法与温度和盐度的计算方法相似。在指定时刻(2001年9月1日0时), 单位浓度的示踪物被释放到指定区域(图1)内的所有网格点的所有σ层上。模型计算时, 各网格点的浓度按如下关系进行变化:

其中,C为示踪物浓度,D为总水深,u、v和ω分别为x、y和σ方向的流速分量,Kv为垂直扩散系数,Fc为水平扩散项,C0为人为设定的源项,∆tI为内模时间步长。C0取值由下式确定:

其中,te,ts=t0±0.5∆tI, 分别为释放示踪物的终止和起始时间(t0为选定的示踪物释放时刻, 这里为 2001年9月1日0时),σ1和σKB分别指σ坐标的上边界和下边界,i为选择释放示踪物的节点号,N为选择释放示踪物的总节点数。

本文滞留时间的计算是基于垂向平均的示踪物浓度, 而实际上湾内任意位置处的表层和底层的示踪物浓度都会有少许不同, 因此我们这里计算的滞留时间只是某个位置处的平均滞留时间, 并没有考虑其垂向的微小差异。另外需要指出, 示踪物会随着涨潮和落潮来回移动, 这使得示踪物浓度的变化具有与潮汐相同的短周期, 但这种短周期的变化不应对估算的滞留时间值产生较大影响。因此, 作者首先用36小时的低通滤波器对深度平均的示踪物浓度进行滤波(可将示踪物浓度随潮汐变化的信号滤掉), 然后计算该点示踪物浓度降为 1/e(0.37)时所用的时间,即为该点的滞留时间。

3　滞留时间计算结果

潮汐、河流和风都是影响水交换的重要因素, 为了区分它们对坦帕湾海水滞留时间的影响程度, 针对坦帕湾海水滞留时间的分析, 我们设定了三组实验 F1、F2和 F3(表1)。这三组实验的驱动力分别为潮汐, 潮汐和河流, 以及潮汐、河流和风。F1实验的设立主要是为了研究在潮汐单独存在时的水交换情况; F2实验主要是为了研究在重力环流影响下的水交换情况; 而通过实验F3和F2的对比, 可以研究风对坦帕湾水交换的影响。这里需要指出, 潮汐、河流和风对水交换的影响并不是简单的线性叠加, 因此,理论上讲我们不可能将它们对水交换的作用完全区分出来。

在F1—F3三种实验情况下, 模型计算91天后坦帕湾的示踪物残留浓度分布以及湾内水体滞留时间的分布见图4—6。在实验F1, 模拟结束后, 示踪物浓度的1/e等值线位于坦帕湾湾口(图4a), 除了湾口的一小部分区域外, 整个坦帕湾的海水滞留时间都长于模型计算时间91天(图4b)。在实验F2, 整个湾内的示踪物残留浓度都有非常明显的降低, 1/e等值线也明显向湾内延伸(图5a)。从此时的滞留时间空间分布(图5b)上可以看到, 几乎整个Lower Tampa Bay的海水滞留时间都短于数值模型计算时间91天。在实验F3, 湾内的示踪物残留浓度进一步降低, 1/e等值线进一步向湾顶延伸并到达Hillsborough Bay(图6a)。此时, 在Lower Tampa Bay 的海水滞留时间进一步缩短,在Hillsborough Bay的东侧以及Middle Tampa Bay也都出现了海水滞留时间短于模型计算时间 91天的区域(图6b)。在图6a中, 我们看到Old Tampa Bay的示踪物残留浓度最大, 表明该区域的水交换能力最弱。

为了便于对比, 我们在坦帕湾内选取了5个网格点(网格点位置见图1), 并将这些网格点上的示踪物残留浓度和滞留时间列于表2。从表2可以看出, 距离坦帕湾湾口越近, 其水体的水交换能力越强。如在F1试验情况下, 靠近口门的 A点的示踪物残留浓度仅为 0.34, 海水滞留时间仅为 2天, 而位于 Middle Tampa Bay 的C点的示踪物残留浓度却为0.90, 海水滞留时间却长于数值模拟时间 91天。另外, 在三种实验下的坦帕湾内部, 都有大量区域的海水滞留时间长于 91天。虽然受数值模型计算时间的限制, 我们无法进一步估计他们准确的滞留时间值, 但是根据所选择的 5个网格点上的示踪物残留浓度分布可以看出, 从实验F1到 F3, 湾内水体的滞留时间有了明显缩短。如位于Hillsborough Bay 的D点, 虽然在F1、F2和F3三种实验情况下其海水滞留时间都长于模型计算时间 91天, 但是其示踪物残留浓度却分别为0.96, 0.54和0.39。因此, 从实验F1到F3, 湾内的示踪物残留浓度有大幅减小, 海水滞留时间有明显缩短, 水交换能力有大幅提高。在选择的5个网格点中, B点位于航道, C点位于其一侧的浅水区域。从他们对应的示踪物残留浓度和滞留时间来看(表2), 无论是在哪种实验情况下, B点的示踪物残留浓度都要比C点的低, 滞留时间比C点的短。因此, 在坦帕湾航道处, 其海水滞留时间的等值线呈现向湾内延伸的舌状形(如图6b)。

这里需要指出, 图4—6和表2中的示踪物浓度分布仅表示在模型计算结束后的瞬时残留浓度分布。虽然我们已经将示踪物浓度的潮周期变化滤掉, 但是受风以及河流的影响, 湾内任意位置处的示踪物浓度的衰减过程依然会有些许波动, 因此其1/e等值线和滞留时间的分布并不完全吻合。

表1　实验设定Tab.1　The experimental design

表2　三种实验情况下网格点A—E的示踪物残留浓度和海水滞留时间Tab.2　The depth-averaged concentration on the 91st day after the release of the passive tracers, and the estimated residence time at the five locations (A—E) for the three experiments (F1—F3)

图4　在实验F1, 示踪物被释放91天后的深度平均的示踪物残留浓度分布(a)和滞留时间分布(b),灰色线表示浓度的1/e等值线Fig.4　The distribution of depth-averaged concentration on the 91st day after the release of the passive tracers (a), and the distribution of residence time (b) for the case F1. The grey lines denote the 0.37 value

4　结果分析

上一节分析了三种实验情况下坦帕湾的海水滞留时间分布有非常大的差别, 这一节将重点分析这些差别产生的原因。在实验F1, 水体的运动主要是受潮汐影响的正压压强梯度力的驱动, 这导致海水垂向近乎均匀的流动(底边界和侧边界因受摩擦力的影响除外)。在这种情况下, 流入和流出海湾的海水只能移动到距离口门一个潮程的范围, 而在一个潮程之外, 海水的更新主要通过水平扩散的方式, 这种方式相对于水平对流作用要弱很多。Weisberg(2011)也有类似的发现。他证明在只有潮的影响下, 海湾的水交换与海湾的水平尺度无关, 而与潮程和海湾长度的比值有关。图7给出了M2分潮的表层潮流椭圆图, 底层的潮流椭圆图和表层相似, 只是振幅稍小, 这里不再给出。从该图上可以看出, 坦帕湾湾口处 M2分潮的潮流振幅较小, 约为30cm/s。潮程的计算由下式确定(Parsaetal, 2010):

图5　同图4, 但为实验F2的结果Fig.5　Same as Fig. 4, but for the case F2

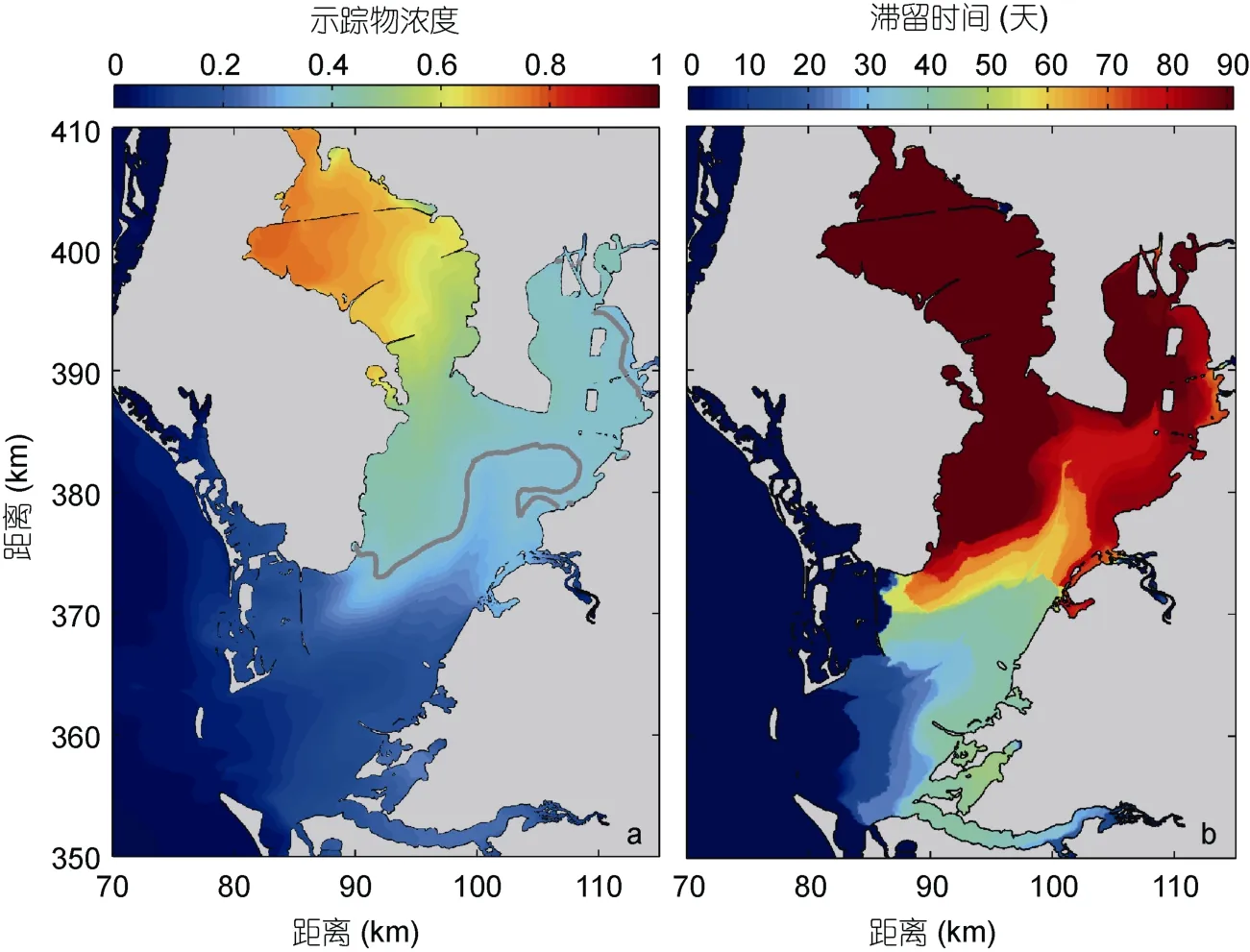
图6　同图4, 但为实验F3的结果Fig.6　Same as Fig. 4, but for the case F3

其中,E为潮程,v0为潮流振幅,T为潮周期。通过上面关系式, 可估算出坦帕湾湾口的 M2分潮的潮程约为4.3km。这与坦帕湾湾口至湾顶的长度 56km相比较小。因此, 在潮汐单独作用时, 坦帕湾的水交换较弱。

另外, 从潮余流的分布来看, 此时湾内的潮致余流场较弱, 分布不规则, 并且充满了漩涡状的结构(表层潮余流的分布见图8)。这与Wang等(2002)的发现一致。这些漩涡状的结构反映了口门、堤坝、航道等复杂岸线地形对环流的影响。这些复杂的漩涡将大量海水限制在其内部, 从而阻碍了湾内与湾外的水交换过程。因此, 在潮汐单独作用时, 坦帕湾的水交换较弱(图4)。底层潮余流的结构和表层相似, 只是流速稍小, 这里不再给出。

图7　M2分潮的表层潮流椭圆图Fig.7　The modeled M2 tidal current hodograph ellipses at surface layer

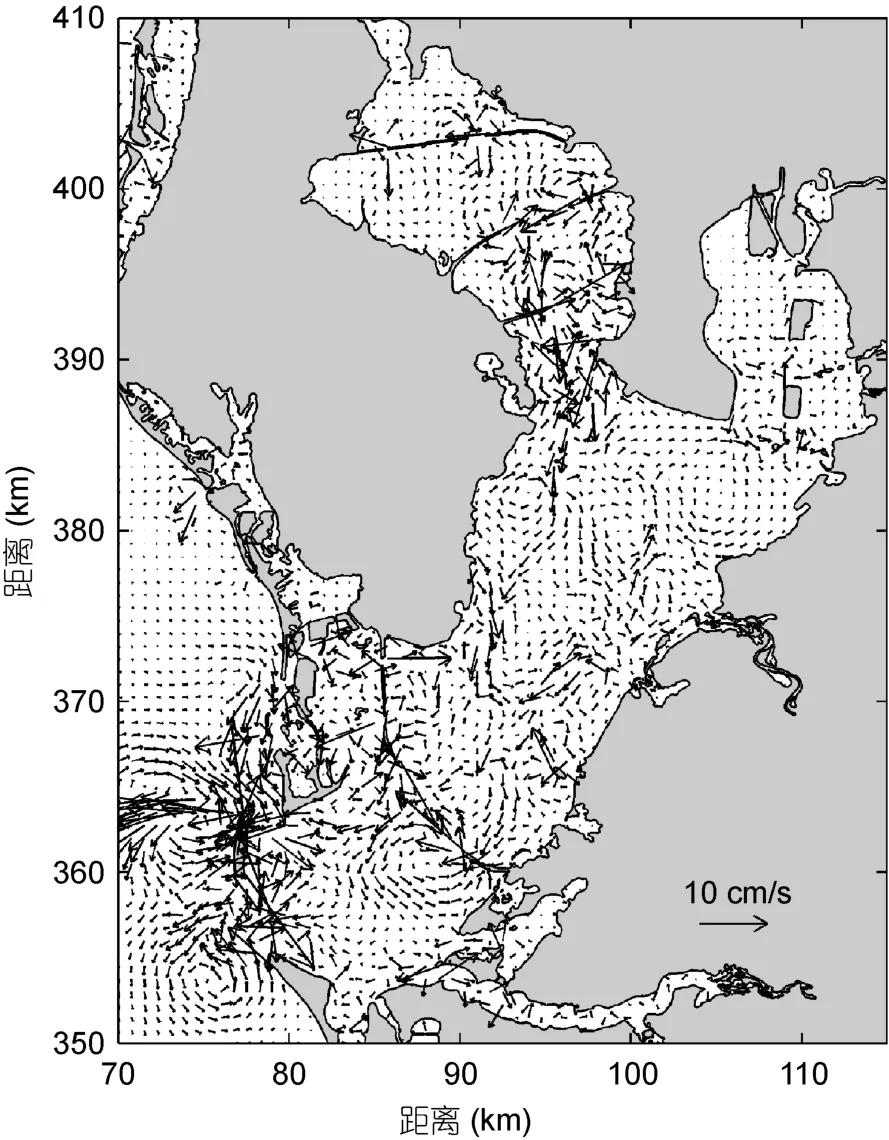
图8　在实验F1情况下的表层潮余流图Fig.8　The residual current at surface layer for case F1

在实验 F2中, 由于河流淡水的输入, 在原有的随潮变化的正压压强梯度力上叠加了指向湾外的正压压强梯度力和指向湾内的斜压压强梯度力。此时非潮水位(non-tidal elevation)的分布如图9a。非潮水位沿坦帕湾轴向向湾顶逐渐增加, 湾顶处非潮水位比湾口处高约3cm。正是在这个由湾顶指向湾口的正压压强梯度力的驱动下, 湾内海水通过表层非潮流(non-tidal current)(图10a)流向湾外。在底层, 由于河流和湾口海水盐度的不同形成了水平密度梯度, 产生了一个由湾口指向湾顶的斜压压强梯度力。在这个斜压压强梯度力的驱动下, 湾外海水通过底层的非潮流(图11a)流向湾内, 并在流向湾内的过程中逐渐上升汇入表层。这个过程使得湾内的水交换能力有了非常明显的提高。

实验F3是接近坦帕湾2001年秋季真实情况下的水交换。在该风场的直接影响下(坦帕湾三个月的平均风速为3.3m/s, 平均风向为67°)(Zhuet al, 2014a),相对于实验 F2, 湾内的非潮水位降低了约 8—12cm(图9c)。这主要是因为在风的影响下, 坦帕湾的表层流得到加强(图10c), 将湾内大量海水带出, 从而导致了湾内水位的降低。在图9a、b中, 我们发现在风的作用下, 坦帕湾湾口和湾顶的水位梯度发生了反转, 水位差由实验F2时的–3cm(图9a)增加到实验F3时的 2cm(图9b)。反转的水位梯度必将产生一个反转的由湾口指向湾顶的水位梯度力, 并进而加强了流向湾内的底层流(图11)。虽然风和河流都能促进坦帕湾的水交换, 但通过上面的分析我们看到, 它们的作用机制是完全不同的。最终, 在坦帕湾 2001年秋季的潮汐、河流以及风的共同作用下, 湾内海水的两层环流得到很大加强, 进而导致了很强的水交换(图6)。

图9　在实验F2 (a) 和F3 (b) 情况下, 坦帕湾非潮水位的分布, (c)为两种情况下的差Fig.9　Distributions of non-tidal elevation throughout Tampa Bay for the cases F2 (a) and F3 (b), and their differences (c)

图10　F2(a) 和F3(b) 情况下, 坦帕湾表层非潮流的分布, (c)为两种情况下的差Fig.10　Distributions of non-tidal current at the surface layer throughout Tampa Bay for the cases F2 (a) and F3 (b), and their differences (c)

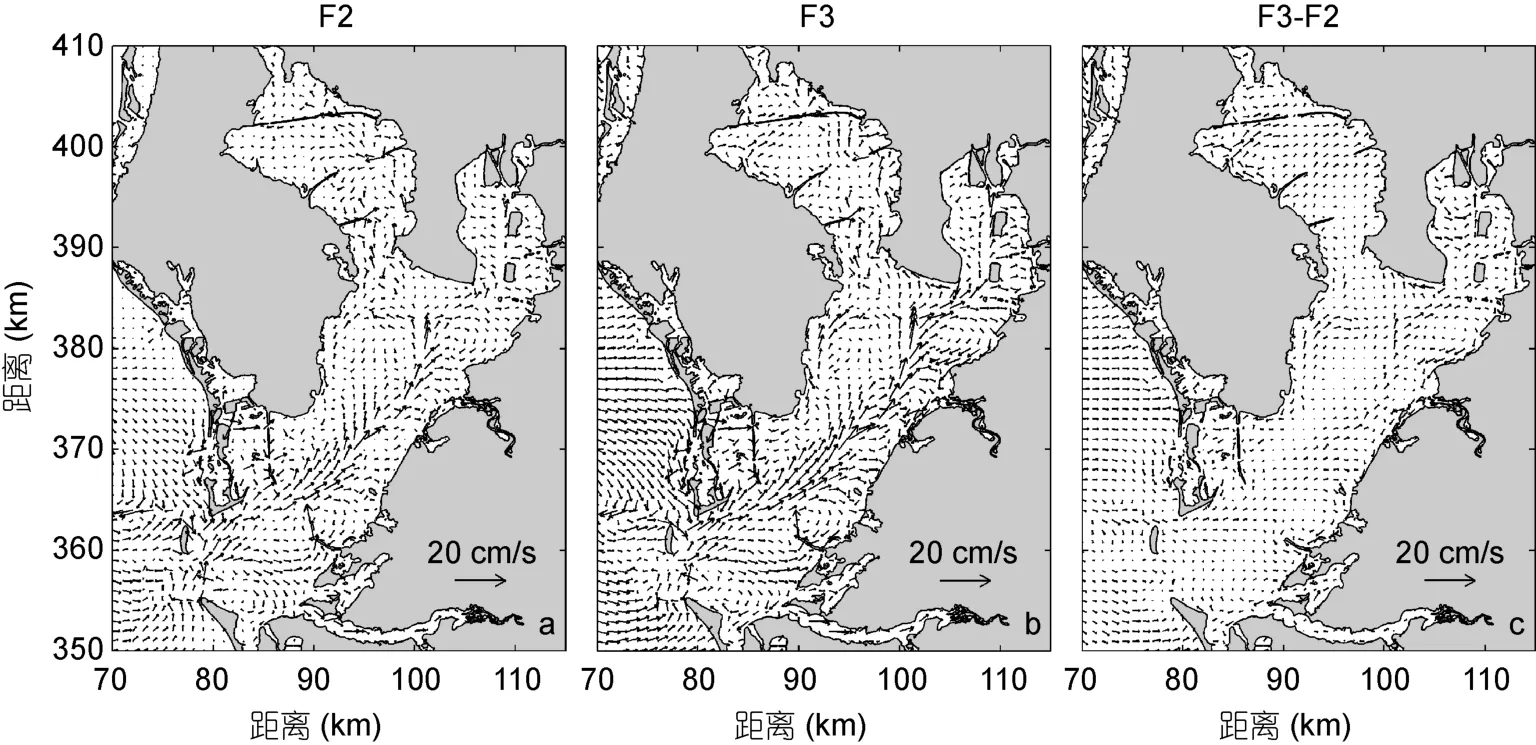
图11　同图10, 但为底层的结果Fig.11　Same as Fig. 10, but for the bottom layer

5　结论

采用 Chen等(2003)的 FVCOM 模式, 以坦帕湾2001年秋季为例, 通过对坦帕湾示踪物浓度三个月的数值模拟, 估算了坦帕湾在不同驱动力下的水交换情况。本文共设定了三组实验, 驱动力分别为潮汐,潮汐和河流以及潮汐、河流和风。通过这三组实验的对比, 分析了影响坦帕湾水交换的三种因素: 潮汐、河流以及风。具体结论如下:

(1) 潮汐单独作用时, 由于坦帕湾的潮汐较弱,潮程较短, 坦帕湾与临近海域的水交换较弱, 并主要发生在湾口附近。

(2) 河流是促进水交换的重要因素, 由于河流和湾口海水盐度的不同形成了水平密度梯度, 在其产生的水平密度梯度力的作用下, 坦帕湾形成了表层流向湾外、底层流向湾内的重力环流, 从而加强了坦帕湾与临近海域的水交换。

(3) 在坦帕湾风应力的影响下, 坦帕湾的表层流得到加强, 同时水位梯度力也发生了反转, 变成了由湾口指向湾顶, 进而加强了流向湾内的底层流。表层流和底层流的加强最终促进了坦帕湾与临近海域的水交换。

(4) 坦帕湾航道的存在促进了湾内的水交换。在航道处, 水深较深瑞利数较大, 该处的重力环流较强,使得水交换能力较强。

(5) 在Old Tampa Bay的西侧和北侧, 水交换能力最弱, 今后应重点加强该地区的生态环境保护, 防止海洋生态灾害的发生。

王聪, 林军, 陈丕茂等, 2008. 大亚湾水交换的数值模拟研究. 南方水产, 4(4): 8—15

褚芹芹, 李磊, 李培良, 2010. 胶州湾潮流场的示踪粒子数值模拟研究. 中国海洋大学学报, 40(11): 29—34

Aikman F, Lanerolle L W J, 2005. Report on the national ocean service workshop on residence/flushing times in bays and estuaries. Silver Spring, Maryland: NOAA Technical Report NOS CS 20

Arega F, Armstrong S, Badr A W, 2008. Modeling of residence time in the East Scott Creek Estuary, South Carolina, USA.Journal of Hydro-environment Research, 2(2): 99—108

Basu B K, Pick F R, 1996. Factors regulating phytoplankton and zooplankton biomass in temperate rivers. Limnology and Oceanography, 41(7): 1572—1577

Burwell, Vincent M, Luther Met al, 2000. Modeling residence times: Eulerian vs Lagrangian.In: Spaulding and Butler eds.Estuarine and Coastal Modeling. Reston: ASCE, 995—1009

Chen C S, Liu H, Beardsley R C, 2003. An unstructured,finite-volume, three-dimensional, primitive equation ocean model: Application to coastal ocean and estuaries. Journal of Atmospheric and Oceanic Technology, 20(1): 159—186

Chen C S, Cowles G, Beardsley R C, 2004. An unstructured grid,finite-volume coastal ocean model: FVCOM user manual.SMAST/UMASSD Technical Report-04-0601, 183

Chen C S, Xu Q, Houghton R,et al, 2008. A model-dye comparison experiment in the tidal mixing front zone on the southern flank of Georges Bank. Journal of Geophysical Research, 113, C02005

Dyer K R, 1973. Estuaries: A physical introduction. Chichester,UK: John Wiley

Egbert G D, Erofeeva S Y, 2002. Efficient inverse modeling of barotropic ocean tides. Journal of Atmospheric and Oceanic Technology, 19(2): 183—204

Goodwin C R, 1987. Tidal-flow, circulation, and flushing changes caused by dredge and fill in Tampa Bay, Florida.Colorado: U S Geological Survey, Water-Supply Paper, 2282

Hagy J D, Sanford L P, Boynton W R, 2000. Estimation of net physical transport and hydraulic residence times for a coastal plain estuary using box models. Estuaries, 23(3):328—340

Havens H, Luther M E, Meyers S Det al, 2010. Lagrangian particle tracking of a toxic dinoflagellate bloom within the Tampa Bay estuary. Marine Pollution Bulletin, 60(12):2233—2241

Hess K, 2001. Generation of tidal datum fields for Tampa Bay and the New York Bight. Silver Spring, Maryland: NOAA Technical Report NOS CS 11, 43

Huang W, Spaulding M, 2002. Modelling residence-time response to freshwater input in Apalachicola Bay, Florida,USA. Hydrological Processes, 16(15): 3051—3064

Ketchum B H, Rawn A M, 1951. The flushing of tidal estuaries.Sewage and Industrial Wastes, 23(2): 198—209

Lewis R R, Estevez E, 1988. Ecology of Tampa Bay, Florida, an Estuarine Profile. Washington D C: U S Department of Interior, Fish and Wildlife Service

Meyers S D, Luther M E, 2008. A numerical simulation of residual circulation in Tampa Bay. Part II: Lagrangian residence time. Estuaries and Coasts, 31(5): 815—827

Miller R L, McPherson B F, 1991. Estimating estuarine flushing and residence times in Charlotte Harbor, Florida, via salt balance and a box model. Limnology and Oceanography,36(3): 602—612

Monsen N E, Cloern J E, Lucas L V,et al, 2002. A comment on the use of flushing time, residence time, and age as transport time scales. Limnology and Oceanography, 47(5): 1545—1553

Officer C B, 1980. Box models revisited. Estuarine and Wetland Processes, Plenum. New York: P. Hamilton and K.MacDonald, 65—114

Oliveira A, Baptista A M, 1997. Diagnostic modeling of residence times in estuaries. Water Resources Research,33(8): 1935—1946

Parsa J, Etemad Shahidi A, 2010. Prediction of tidal excursion length in estuaries due to the environmental changes.International Journal of Environmental Science and Technology, 7(4), 675—686

Sanford L P, Boicourt W C, Rives S R, 1992. Model for estimating tidal flushing of small embayments. Journal of Waterways, Ports, Coastal and Ocean Engineering, 118(6):635—654

Sheldon J E, Alber M, 2002. A comparison of residence time calculations using simple compartment models of the Altamaha River Estuary, Georgia. Estuaries, 25(6B):1304—1317

Wang, Z B, Jeuken M, Gerritsen Het al, 2002. Morphology and asymmetry of the vertical tide in the Westerschelde estuary.Continental Shelf Research, 22(17): 2599—2609

Warner J C, Geyer W R, Arango H G, 2010. Using a composite grid approach in a complex coastal domain to estimate estuarine residence time. Computers and Geosciences, 36(7):921—935

Weisberg R H, Zheng L Y, 2006. Circulation of Tampa Bay driven by buoyancy, tides, and winds, as simulated using a Finite Volume Coastal Ocean Model. Journal of Geophysical Research, 111, C01005

Weisberg R H, 2011. Coastal ocean pollution, water quality, and ecology. Marine Technology Society Journal, 45(2): 35—42

Yuan D, Lin B, Falconer R A, 2007. A modelling study of residence time in a macro-tidal estuary. Estuarine, Coastal and Shelf Science, 71(3—4): 401—441

Zhang W G, Wilkin J L, Schofield O M E, 2010. Simulation of Water Age and Residence Time in New York Bight. Journal of Physical Oceanography, 40(5): 965—982

Zheng L Y, Weisberg R H, 2012. Modeling the west Florida coastal ocean by downscaling from the deep ocean, across the continental shelf and into the estuaries. Ocean Modelling,48(5): 10—29

Zhu J, Weisberg R H, Zheng L Yet al, 2014a. Influences of channel deepening and widening on the tidal and non-tidal circulation of Tampa Bay. Estuaries and Coasts,http://dx.doi.org/10.1007/s12237-014-9815-4

Zhu J, Weisberg R H, Zheng L Yet al, 2014b. On the flushing of Tampa Bay. Estuaries and Coasts, http://dx.doi.org/10.1007/s12237-014-9793-6

Zimmerman J T F, 1988. Estuarine Residence Times. In: Kjerfve B ed. Hydrodynamics of Estuaries, vol. 1. Boca Raton,Florida: CRC Press, 75—84