基于高效数值方法的高速飞行器气动力热特性快速预测研究

王 荣，张学军，纪楚群

(中国航天空气动力技术研究院，北京 100074)

基于高效数值方法的高速飞行器气动力热特性快速预测研究

王 荣*，张学军，纪楚群

(中国航天空气动力技术研究院，北京 100074)

结合空间推进数值模拟方法和流线追踪法发展了气动力、热快速预测技术。针对高速飞行器的算例研究表明，相对常规时间推进方法，基于空间推进法的气动快速预测方法计算效率提高了一个量级，而两者气动力计算精度相当，相对实验热流预测误差在20%以内。所发展的技术为适应气动外形快速选型和优化设计需求提供了有效的方法。

空间推进;流线追踪;高速飞行器

0 引言

飞行器设计面向的气动外形越来越复杂，对气动力和气动热性能预测评估技术也提出了更高的要求，一方面要求预测精度更好，另一方面要求预测评估时间愈短愈好。尤其是在选型设计阶段和气动外形优化设计方面更迫切地需要建立气动力热特性的快速预测评估技术。

精度和效率往往是有冲突的，目前气动力热预测广泛采用的方法有工程方法和基于时间相关法(时间推进法)的CFD数值方法。纯工程计算方法计算量小，可以在短时间内完成大量的计算，但是计算精度不够理想。CFD方法计算精度与工程方法相比具有非常明显的优势，但缺点是计算量非常大，计算成本较高。

对于主流方向无分离的超声速流动，可采用空间推进方法沿主流方向高效推进求解。相对纯工程方法和时间推进方法，该方法相对高效同时能够保持精度。因此，近些年国内外针对抛物化NS方程(PNS)采用空间推进方法的计算工作很多［1-5］。由于PNS需要计算粘性项，对网格要求较高，边界层网格密度大。根据边界层理论［6］，粘性主要作用于薄边界层，流场外层可看作是无粘流动。因此可先采用无粘欧拉方程通过空间推进法快速求解外层流场，以此得到的边界层外缘参数为基础，再采用流线追踪工程方法快速求出热流。这种将无粘高效数值方法和工程方法相结合预测气动力热性能的方法，相对PNS方法无需求解粘性项可减少一定的计算量，同时也降低了对网格的要求，相对于采用时间推进法［6-8］获得边界层外缘无粘流场参数的做法耗时少，更加快速高效。

对于超声速流动，扰动仅向下游传播，此时定常Euler方程为流向初值适定［1］的拟线性双曲型方程，在给定初始横流面流场解条件下，可通过空间推进求解，且推进一次就可得到流场解。初值面可通过时间相关法求出，由于求解初值面仅需很少的网格，耗时是比较少的。因此总的来讲，基于定常Euler方程空间推进求解方法计算效率高，鲁棒性好，在一定马赫数和迎角范围可满足工程型号复杂外形气动特性快速评估要求。

沿流线气动加热积分计算的方法是由Zoby［9］于上世纪80年代初提出的，Zoby基于对轴对称边界层动量方程的分析并结合Eckert参考焓概念给出了可压缩条件下物面摩阻与边界层动量厚度之间的积分关系式，而后运用“修正雷诺比拟”给出适用于变熵条件的层流、湍流气动加热率计算的积分关系式;这些关系式结合“轴对称比拟法”技术可用于一般三维外形气动加热的预测。“轴对称比拟法”最早由Cooke［10］提出并由DeJarnette［11］等人通过实践而成为一种实用的技术。运用轴对称比拟技术可将三维边界层问题转化为轴对称边界层问题，所有适用于轴对称条件的气动加热率的计算公式都可用于计算一般的三维外形。该气动加热快速预测方法与纯粹的数值模拟技术相比具有耗时少、精度轻微损失的特点，适于预测比较复杂的三维外形的热流。

因此，本文针对工程上几何形状比较复杂的三维高速飞行器外形，基于空间推进求解无粘方程的高效数值方法和流线追踪工程方法，将二者结合建立了有一定精度的可满足工程应用要求的气动力热特性快速预测方法。气动力预测基于高效空间推进数值方法，气动热预测采用流线追踪法基于空间推进无粘数值解与轴对称比拟的气动加热积分关系式。

1 气动力热性能高效预测方法

1.1 无粘流场空间推进法

本文无粘流场计算通过空间推进法数值求解Euler方程完成。推进方向采用预测-校正两步法，侧面通量求解基于Godunov格式，根据Van Leer方法构造二阶精度，对梯度用Minmod限制器进行单调性限制。方法细节见文献［12-14］。

1.2 气动加热预测方法

所有气动加热快速预测方法的基础是基于对边界层方程的变换和求解。本文气动加热预测方法采用流线追踪法，首先通过采用上述空间推进的方法数值求解Euler方程获得无粘流场，然后利用无粘流场计算结果确定物面流线及尺度因子，沿流线运用Zoby［9］的方法积分得到物面气动加热率。在积分的每一步计算当地的边界层厚度，插值得到无粘流场在该位置处的流动参数作为边界层外缘参数。

2 网格划分

本文在推进计算前，先生成整体三维网格，然后根据推进过程，下一个站位二维网格从三维网格中插值得到，这样可以有效地解决推进过程中生成网格的问题。网格生成采用单体结构网格划分技术，划分步骤为，首先对每个轴向站位生成二维网格面，然后连接从头部至底部各站位网格面最终建立三维空间网格。各站位的二维网格面通过数值求解抛物化方程从物面逐步推进到外流场边界完成，由于抛物化推进方法较成熟，容易控制网格的稀密及正交等特性，因此对一般外形均可得到质量较好的网格分布。

3 高速飞行器外形气动力热算例研究

本文气动力热快速预测方法在高速飞行器外形气动特性计算中得到成功应用，以下给出应用算例。

3.1 升力体外形

针对一种扁尖型升力体外形，运用本文所发展的方法完成了气动力热特性计算，外形如图1所示。图2给出了M=3.0和10.0，采用空间推进法(sm)计算的法向力系数CN，轴向力系数CA和对质心俯仰力矩系数Cmzg随迎角变化曲线与时间相关法(tm)计算结果比较。两种方法得到的气动力系数符合很好，证明了空间推进法气动特性预测的准确性。

图1 升力体外形Fig.1 Lift-body configuration

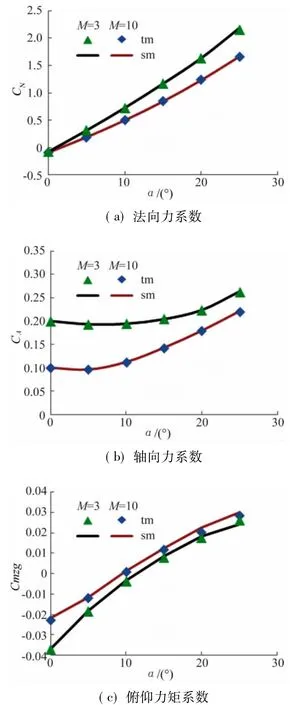
图2 空间推进法与时间相关法计算比较Fig.2 Aerodynamic coefficient compare between space and time marching methods

图3为M=10.0、α=20°时采用空间推进法计算的升力体外形物面和流场典型截面压力分布图，图4为物面热流分布情况。

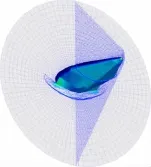
图3 升力体外形物面和典型截面压力分布Fig.3 Pressure distribution of the vehicle

图4 升力体外形物面热流分布(M=10.0、α=20°)Fig.4 Heat flux on the vehicle surface

3.2 空天飞机外形

根据文献［15］给出的空天飞机外形(基本型)地面试验结果，对本文所发展的气动力热快速预测方法进一步进行了验证计算。该外形机身采用半圆和矩形组合横截面，机翼为大后掠三角翼，翼端上弯。实验模型全长0.29 m，翼前缘后掠角 68°，翼展0.1848 m，头部半锥角10°，球头半径0.015 m，外形如图5所示。

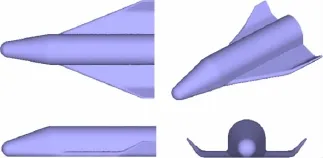
图5 空天飞机试验外形Fig.5 Space shuttle

图6给出了M=8.0，α=20°时，使用空间推进法计算的机身中心迎风线(windward)和背分线(leeward)与实验的比较，可以看出，计算(sm cal)和实验(exp)规律一致，数据符合性也比较好;图7和图8分别为机身两个横截面和机翼弦向两个截面计算与实验比较结果，在背风面计算偏小，总体上两者一致性较好。图9为该状态的计算网格，轴向站位网格点为30×58，网格总数约17万。图10为推进计算得到的五个站位压力云图，各站位压力分布和激波形态是合理的。

图6 M=8.0、α=20°空间推进法和实验物面轴向压力比较Fig.6 Pressure compare between experiment data and computational results of the symmetry plane

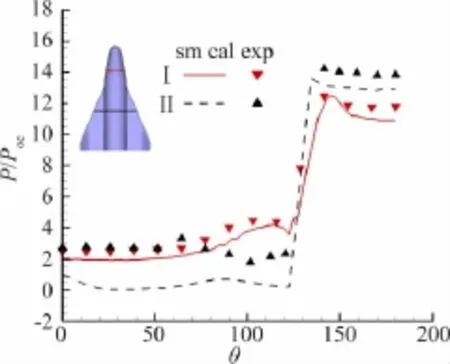
图7 M=8.0、α=20°空间推进法和实验物面周向压力比较Fig.7 The circular pressure of two cross sections

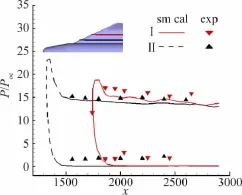
图8 M=8.0、α=20°空间推进法和实验翼面弦向压力比较Fig.8 The pressure of wing chord section

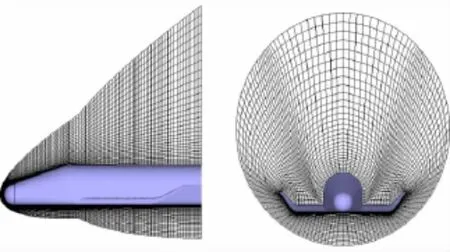
图9 空间推进计算网格(M=8，α=20°)Fig.9 The corresponding grids

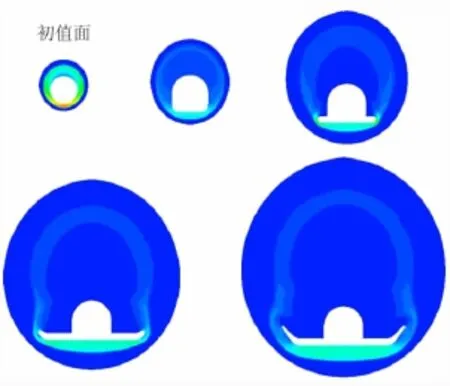
图10 五个站位空间推进压力云图(M=8，α=20°)Fig.10 Pressure of five cross sections

以上计算工况在主频为2.8GHz的CPU上计算时间见下表1，相对时间相关法，空间推进时间消耗下降接近一个量级。

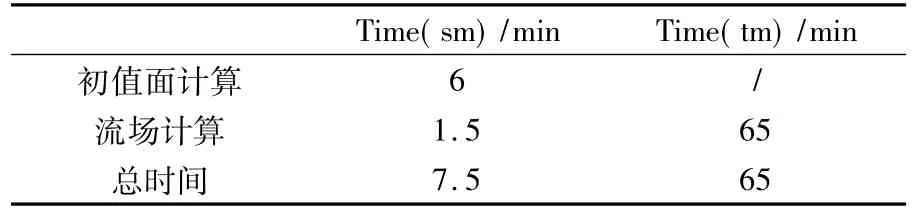
表1 空间推进与时间迭代法计算效率对比Table 1 The efficiency of the two methods

图11给出了M=4.0时空间推进法计算的CN，CA和Xcp随迎角变化曲线与时间推进法及实验结果比较。可以看出，空间推进法与时间相关法得到的气动力系数均符合很好，计算与实验法向力系数一致性很好，轴向力系数在大迎角时偏差增大，总的来看计算与实验有较好的一致性。

图12给出马赫8、迎角20°，试验状态单位雷诺数为Re=3.54×107/m时，航天飞机机身迎风中心线热流的计算值与实验值的对比情况，计算时认为在机身前部就已完成转捩并达到完全湍流流态。物面无粘流线分布见图13。对比表明，虽然实验数据本身散布度比较大，但计算的曲线经过散布点中间区域，且两者趋势相符合。实验值与计算值的相对偏差范围在2.7%～27.4%之间，21个测点中有17个测点的相对偏差小于20%。

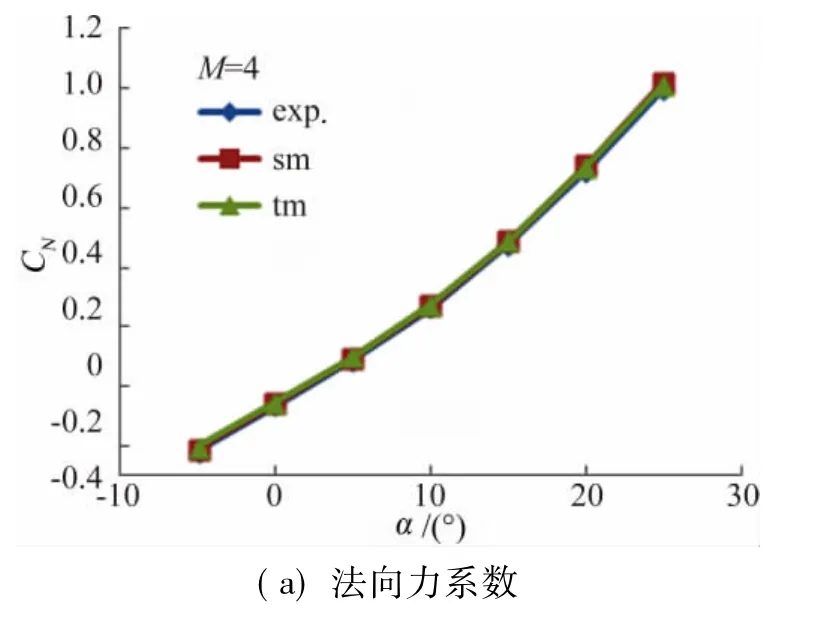
图11 M=4.0空间推进法计算与时间相关法和实验数据比较Fig.11 Compare results of the two methods and tests

图12 机身中心迎风线热流计算与实验比较(湍流)Fig.12 Central line heat flux on the windward side(turbulence)

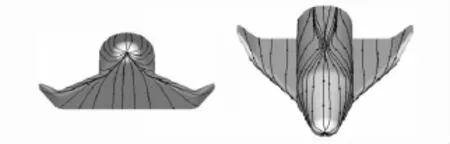
图13 空天飞机外形上、下表面无粘流线分布图(M=8.0、α=20°)Fig.13 Stream lines on the surface(M=8.0、α=20°)

马赫10、迎角18°时，试验状态的单位雷诺数为Re=2.2×106/m，计算时认为机身迎风线为完全层流流态，翼面迎风侧已完成转捩达到了完全湍流流态。图14和图15分别给出机身和翼面迎风线热流的计算值与实验值的对比。对于机身，实验数据本身散布度不大，计算与实验符合较好。实验值与计算值的相对偏差范围在0.1%～33.9%之间，13个测点中有12个测点的相对偏差小于20%。翼面实验值与计算值的相对偏差范围在0.3%～16.3%之间。

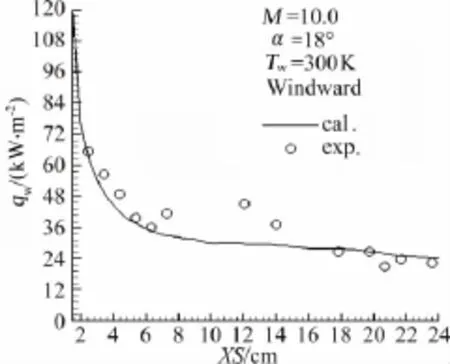
图14 机身中心迎风线热流计算与实验比较(层流)Fig.14 Central line heat flux(laminar)

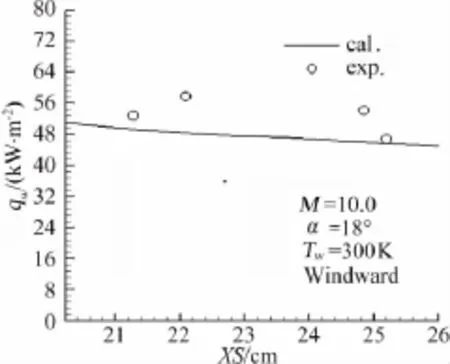
图15 迎风翼面热流计算与实验对比曲线(湍流)Fig.15 Heat flux of the wing windward side(turbulence)

4 结论

本文建立的气动力热特性快速预测方法有较好的预测精度和效率。通过算例研究表明气动力特性空间推进快速预测方法计算与实验有很好的一致性，并且计算效率较高，同样情况下空间推进法比时间相关法耗时可降低一个量级。气动加热快速预测方法与纯粹的数值模拟技术相比具有耗时少、预测精度轻微损失的特点，计算结果与地面试验数据的对比表明，此方法可以比较准确的预测迎风区的气动加热率，二者的相对偏差不高于20%。

本文所发展的气动力热特性快速预测技术，为高速飞行器气动外形快速选型设计和气动外形优化设计奠定了基础。

［1］ Lawrence S L，et al.Application of an upwind algorithm to thethree-dimensional parabolized Navier-Stokes equations［R］.AIAA-87-1112，1987.

［2］ Gao Zhi.Significance and use of basic equation system governing high Reynolds number flows and diffusion-parabolized Navier-Stokes equations［J］.Advances in Mechanics，2005，35(3):427-438.(in Chinese))

高智.高雷诺数流动的控制方程体系和扩散抛物化Navier-Stokes方程组的意义和用途［J］.力学进展，2005，35(3):427-438.

［3］ Birch T J，Prince S A，Simpson G M.IMPNS:A space-marching solver for predicting theaerodynamic characteristics of high-speed missiles［R］.AIAA 2002-4512.

［4］ Chen Bing，Xu Xu，Cai Guobiao.Numerical simulation of hypersonic Inlet flows using a parabolized Navier-Stokes algorithm［J］.Journal of Astronautics，2006，27(6):1319-1323.(in Chinese)

陈兵，徐旭，蔡国飙，等.用空间推进算法模拟高超声速进气道流场［J］.宇航学报，2006，27(6):1319-1323.

［5］ He Xuzhao，Le Jialing.Solving PNS equations with space marching method and it’s validation［J］.Acta Aerodynamic Sinica，2007，25(2):189-193.(in Chinese)

贺旭照，乐嘉陵.空间推进方法求解抛物化Navier-Stokes方程及其验证［J］.空气动力学学报，2007，25(2):189-193.

［6］ Han Dong，Fang Lei.Study of aerodynamic heating predictions for hypersonic aircrafts by tracing the surface stream trace［J］.Journal of Aerospace Power，2009，24(1):65-69.(in Chinese)

韩冬，方磊.基于流线跟踪法的气动热工程计算研究［J］.航空动力学报，2009，24(1):65-69.

［7］ Lv Lili，Zhang Weiwei，Ye Zhengyin.Predicting heating distributions for hypersonic reentry bodies［J］.Chinese Journal of Applied Mechanics，2006，23(2):259-262.(in Chinese)

吕丽丽，张伟伟，叶正寅.高超声速再入体表面热流计算［J］.应用力学学报，2006，23(2):259-262.

［8］ Kang Honglin，Yan Chao，Li Tinghe.Numerical study of aeroheating predictions for hypersonic reentry bodies［J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32(12):1395-1398.(in Chinese)

康宏琳，阎超，李亭鹤.高超声速再入钝头体表面热流计算［J］.北京航空航天大学学报，2006，32(12):1395-1398.

［9］ Zoby E V.Approximate convective-heating equations for hypersonic flows［R］.AIAA 79-1078R.

［10］Cook J C.An axially symmetric analogue for general three-dimensional boundary layers［J］.R＆M No.3200，British A.R.C.1961.

［11］DeJarnette，Fred R.Aerodynamic heating on complex configurations［C］//Technical papers conference on Advanced Technology for Future Space Systems，May 1979:179-188(AIAA paper 79-0891).

［12］Ji Chuqun.Missile aerodynamics［M］.Beijing:China Astronautic Publishing House，1996.(in Chinese))

纪楚群主编.导弹空气动力学［M］.北京:宇航出版社，1996.

［13］Ji Chuqun，Li Jun.Application of the Godunov method in the numerical simulation of complicated flow fields［J］.Acta Aerodynamica Sinica，2000，18(2):132-137.(in Chinese)

纪楚群，李骏.Godunov方法在复杂流场数值模拟中的应用［J］.空气动力学学报，2000，18(2):132-137.

［14］Mendenhall M R.Tactical missile aerodynamics:prediction methodology［M］.Beijing:China Astronautic Publishing House，1999.(in Chinese) Mendenhall M R(美)主编，洪金森等译.战术导弹空气动力学［M］.北京:宇航出版社，1999.

［15］Li Suxun.Hypersonic flow characteristics for typical shapes［M］.Beijing:National Defense Industry Press，2007.(in Chinese)

李素循.典型外形高超声速流动特性［M］.北京:国防工业出版社，2007.

Fast prediction based on effective numerical method for aerodynamic force and heat of high speed vehicles

Wang Rong*，Zhang Xuejun，Ji Chuqun
(The First Institute，China Academy of Aerospace Aerodynamics，Beijing 100074，China)

A fast aerodynamic characteristics prediction technique is developed to predict aerodynamic force and heat，combining effective space marching numerical method with engineering method based on surface stream tracking technique.Hypersonic aerodynamic forces are obtained effectively by solving the Euler equations numerically with fast space marching method.In order to calculate the heat flux，an engineering method，called tracking the surface stream trace based on the axisymmetric analogue technique and boundary layer theory，is adopted and developed to be applicable for complex geometry.The inviscid flow parameters and surface stream lines required in the engineering method are obtained from above mentioned inviscous numerical flow fields.The proposed method for aerodynamic force and heat prediction is applied to high speed vehicles，the results show that the space marching method saves the computational cost enormously，approximately one order less comparing to the time marching method，while the two methods have similar precision in aerodynamic force evaluation.The predicted error of heat flux is within 20%comparing to that of wind tunnel test.The technique promoted is an effective approach suitable for the needs of fast aerodynamic configuration design and optimization.

space marching;stream trace;high speed vehicle

V211.3

A

10.7638/kqdlxxb-2014.0003

0258-1825(2015)04-0530-06

2014-02-11;

2014-05-09

王荣*(1981-)，男，高级工程师，研究方向:气动计算与布局优化设计.E-mail:dilect@126.com

王荣，张学军，纪楚群.基于高效数值方法的高速飞行器气动力热特性快速预测研究［J］.空气动力学学报，2015，33(4):530-535.

10.7638/kqdlxxb-2014.0003 Wang R，Zhang X J，Ji C Q.Fast prediction based on effective numerical method for aerodynamic force and heat of high speed vehicles［J］.Acta Aerodynamica Sinica，2015，33(4):530-535.