整体双锥形环件闭式径向辗轧毛坯尺寸的设计方法

李兰云，李 霄，刘 静，谷瑞杰，何 志

(1.西安石油大学材料科学与工程学院材料加工重点实验室，陕西 西安 710065;2.汽车零部件先进制造技术教育部重点实验室(重庆理工大学)，重庆 400054;3.华中科技大学材料成形与模具技术国家重点实验室，湖北 武汉 430074;4.中国重型机械研究院股份公司，陕西 西安 710032;5.金属挤压/锻造装备技术国家重点实验室，陕西 西安 710032)

0 前言

环件辗轧作为精确塑性成形研究前沿领域的一个重要方向，具有省力、节能、节材、效率高、成本低、产品性能好等显著优点，是目前世界各国石油化工、能源机械和航空航天等高技术领域中的环类零件成形制造实现轻量化、精确化、柔性化、高性能、低成本和短周期的重要途径［1，2］。环件辗轧通常分为径向辗轧和径轴向辗轧两种，均是利用轧辊的旋转驱动和直线进给作用使毛坯连续咬入轧制孔型，产生壁厚减薄、直径增大、截面轮廓成形的连续局部塑性变形，进而直接获得复杂截面轮廓形状的环类产品［3，4］。然而，在环件辗轧成形工艺过程中由于同时存在直径扩大运动和复杂截面形成，因此研究毛坯尺寸设计方法以合理分配不均匀变形量，这不仅是实现环件辗轧顺利开展并稳定进行的前提条件，而且在获得具有精确形状尺寸和精准组织性能的高性能环件方面具有重要作用［5，6］。

迄今为止，国内外学者对环件辗轧毛坯设计进行了一些简单研究。在环件径向辗轧毛坯设计方面，Qian 等分别研究了T 形截面环件［7］和台阶形截面环件［8］辗轧毛坯设计优化，但其主要思想是先直接给定不同形状的毛坯尺寸，然后采用理论解析、试验或者有限元仿真的方法研究给定毛坯辗轧过程的变形行为，从而实现毛坯形状的优选。在环件径轴向辗轧毛坯设计方面，Keeton［9］提出了一个基于毛坯瞬时高度和瞬时壁厚的数学公式来设计矩形截面环件径轴向辗轧的毛坯，该方法虽可避免成形缺陷，但对于某一个环件辗轧在给定芯辊直径的前提下只能设计出唯一的毛坯，且这个毛坯也不一定是最优的;Kang等［10］提出了基于刚塑性有限元法的反向模拟方法用于环件辗轧的毛坯尺寸设计，但由于环件辗轧过程的几何、边界和物理三重非线性导致其计算效率不高;郭良刚等［11］针对矩形截面环件径轴向辗轧的三种变形形式，提出了一种毛坯尺寸设计方法，但该方法无法推广到异形截面环件辗轧毛坯设计中。

然而，近年来各种异形截面环件的需求量不断增加、品种越来越多、尺寸越来越大、所用材料种类也日益呈现多样化，这些都需要更为先进的毛坯设计技术与之相适应。整体双锥形环件是一种典型的异形截面环件，被广泛应用于石油、化工、风电、航空、航天、汽车、轴承等工业领域中［12］。因此，本文将以整体双锥形环件闭式径向辗轧为例，研究一种基于辗轧比的毛坯尺寸设计新方法，以期为异形环件辗轧毛坯尺寸设计提供一种新的思路和借鉴。

1 基于体积不变原理确定毛坯尺寸计算公式

1.1 毛坯结构设计

假设最终成形的环件为如图1a 所示的整体双锥形环件，其中RRL、RRM、RRS、HR、α 分别表示整体双锥形环件的外半径、端面半径、内半径、轴向高度和锥形角。VR和SR分别为整体双锥形环件的体积和截面积。

因整体双锥形环件是一种较为复杂的异形环件，若直接采用矩形截面毛坯则辗轧成形过程中金属流动异常复杂，各项工艺参数较难设计和控制，且辗轧成形的产品的精度和性能均难以满足设计要求。为有效避免这一问题，本文选用如图1b 所示的双锥形截面毛坯，其中RBL、RBM、RBS、HB分别表示双锥形截面毛坯的外半径、端面半径、内半径和轴向高度。采用这种形状毛坯的最大特点是使得双锥形截面毛坯的锥形角等于整体双锥形环件的锥形角，从而可以减少径向辗轧过程的复杂度。VB和SB分别为双锥形截面毛坯的体积和截面积。

基于整体双锥形环件和所设计的双锥形截面毛坯的结构，根据闭式径向辗轧的原理设计出的芯辊如图1c 所示，其中RML和RMS分别为芯辊的大端外半径和小端外半径。另外，这种芯辊的轴向高度也等于HR，且锥形角也等于整体双锥形环件的锥形角。

1.2 确定毛坯尺寸设计公式

根据塑性成形中的体积不变原理有

同时根据辗轧比λ为辗轧前毛坯截面积与辗轧后环件截面积之比的定义有

由图1b 可知:

同时还可以得到

图1 环件、毛坯和芯辊示意图Fig.1 Schematic diagram of ring part，ring blank and mandrel

将式(2)、(5)代入式(3)中可得

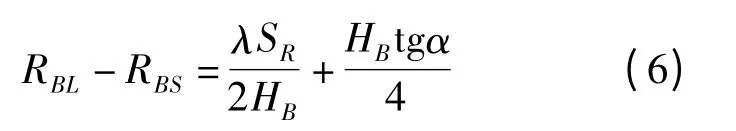
再将式(1)和式(5)代入式(4)中可得

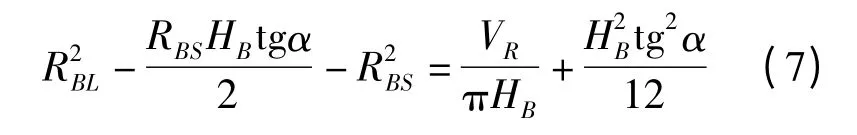
由于选用的成形方式为闭式径向辗轧，故有

将式(8)代入式(6)和式(7)，则

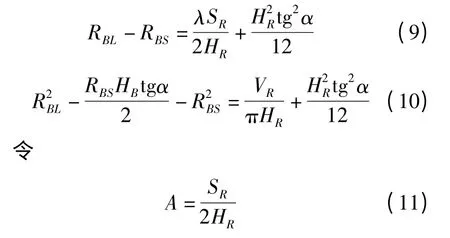
则式(9)和式(10)变为

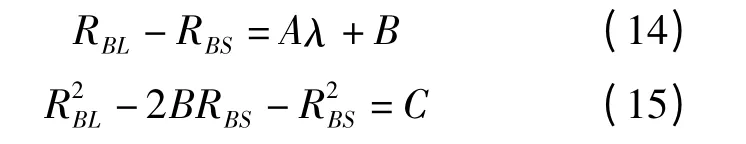
联立式(14)和式(15)求解可得:

再将式(12)和式(17)代入式(5)中可得:

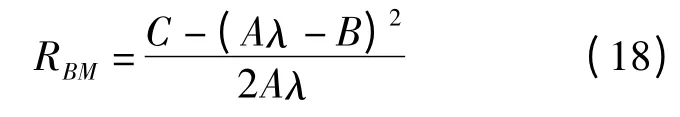
因此，整体双锥形毛坯的外半径RBL、端面半径RBM、内半径RBS和轴向高度HB分别按式(16)、式(18)、式(17)和式(8)进行确定，而其中A、B、C 的值由式(11)～式(13)确定。

2 基于稳定成形条件确定辗轧比的取值范围

根据环件辗轧成形原理，为使整个整体双锥形环件闭式径向辗轧成形过程能顺利地开展并稳定地进行，需满足如下三项基本条件:

(1)条件1。辗轧比必须大于1，即

(2)条件2。在环件径向辗轧过程中，芯辊朝驱动辊的连续进给使得环件的壁厚不断减薄、半径不断长大、截面轮廓逐渐成形。因此毛坯的壁厚应大于环件的径向壁厚，且毛坯的半径应分别小于环件的半径。即

(3)条件3。毛坯的半径必须大于芯辊的半径，这样才能保证将芯辊放入毛坯内。即

根据条件1 中直接给出的辗轧比的取值范围，依次考虑条件2 和条件3 来获得辗轧比取值范围。

2.1 考虑条件2 的辗轧比取值范围

(1)由WBL＞WRL得

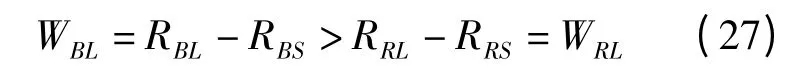
将式(14)代入式(27)后有

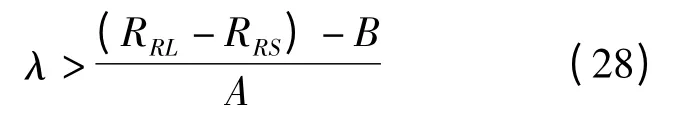
(2)WBS＞WRS得

由于HB=HR，故只要当WBL＞WRL满足时，WBS＞WRS也就自动满足了。

(3)RBS＜RRS。将式(17)代入式(22)中有

变形后有

A2λ2+2A(B+RRS)λ+(B2－C)＞0 (32)由式(11)～式(13)可知A、B、C 均大于0，进而可知总是成立的，故

(4)RBM＜RRM。

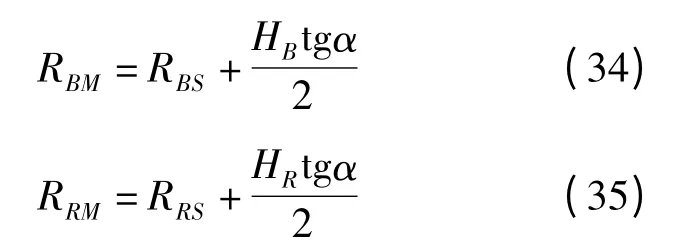
由于HB=HR，故只要当RBS＜RRS满足时，RBM＜RRM也就自动满足了。

(5)RBL＜RRL。将式(16)代入式(24)中有

变形后有

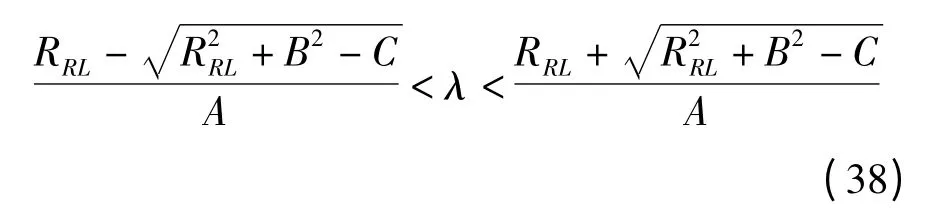
2.2 考虑条件3 的辗轧比取值范围

(1)RBS＞RMS。将式(17)代入式(25)中有

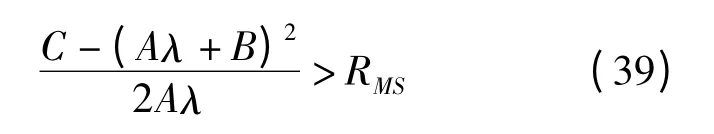
变形后有

因为Δ40=4A2(R2MS+2BRMS+C)＞0 总是成立的，故由式(40)可得

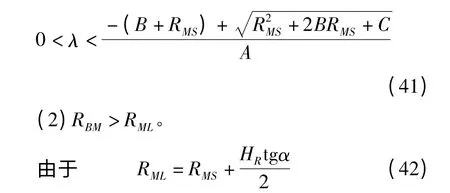
只要当RBS＞RMS满足时，所以RBM＞RML也就自动满足了。

2.3 综合确定辗轧比的取值范围

最后，综合考虑上述条件，由图1 得

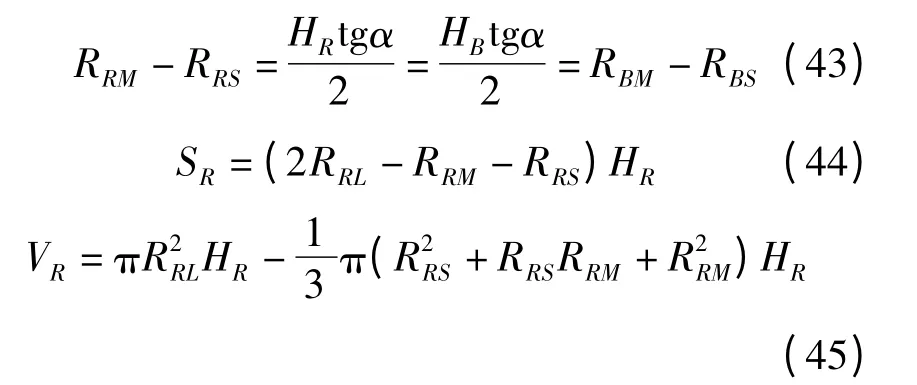
同时结合A、B、C 定义可以推导得

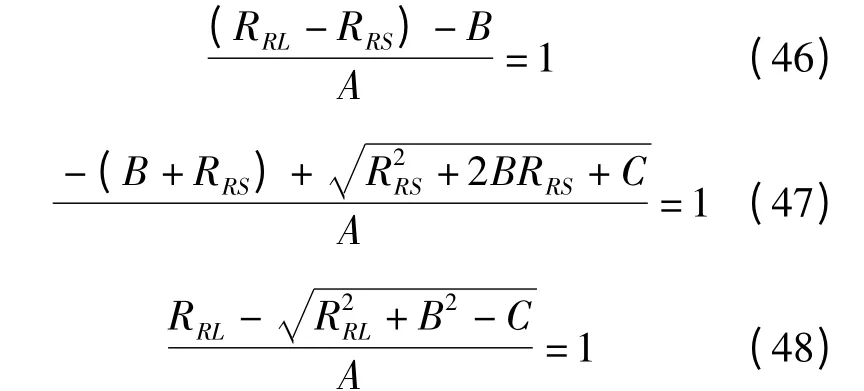
3 基于辗轧比的毛坯尺寸设计新方法

在给定如图1a 所示的整体双锥形环件尺寸(具体包括:外半径RRL、端面半径RRM、内半径RRS、轴向高度HR和锥形角α)的条件下，本文提出了一种基于辗轧比的双锥形截面毛坯尺寸设计新方法，其具体步骤为

(1)确定整体双锥形环件闭式径向辗轧过程中的初始毛坯为如图1b 所示的双锥形截面毛坯;

(2)确定出如图1c 所示的芯辊的大端外半径RML和小端外半径RMS取值;

(3)按式(45)和式(44)分别计算出整体双锥形环件的体积VR和截面积SR;

(4)按式(49)计算出整体双锥形环件闭式径向辗轧成形过程中辗轧比λ 的合理取值范围;

(5)在所计算出的辗轧比λ 的合理取值范围内任意选择一个λ 值;

(6)将上述取值代入到式(16)、式(18)、式(17)和式(8)中就可分别计算出双锥形截面毛坯的外半径RBL、端面半径RBM、内半径RBS和轴向高度HB;

根据上述过程可知:若选择辗轧比λ 取值不同，则计算得到的双锥形截面毛坯尺寸取值也不同;但是这些尺寸取值都是符合设计要求的。因此，可见所提出方法特点是:只需获得最终整体双锥形截面环件的几何尺寸以及芯辊的外半径，就可以快速确定出辗轧比λ 的取值范围;然后结合在确定的辗轧比λ 范围内所选取的辗轧比λ 值就可以快速确定双锥形截面毛坯尺寸。

4 设计实例

若最终整体双锥形环件的外半径RRL为90 mm、端面半径RRM为85 mm、内半径RRS为75 mm、轴向高度HR为30 mm。并假设芯辊小端外半径RMS为35 mm。

根据给定的整体双锥形环件尺寸可计算出其截面积SR=600 mm2和体积VR=159355 mm3，可计算出辗轧比λ 合理取值范围为［1.00，1.74］。因此，辗轧比λ 可在［1.00，1.74］取任何一个值。最后，选取一个辗轧比λ 值，就可计算出双锥形截面毛坯的外半径RBL、端面半径RBM、内半径RBS和轴向高度HB。表1 给出了选取七个不同辗轧比λ 值计算得到的双锥形截面毛坯尺寸。该方法针对同一尺寸的整体双锥形环件产品，能够设计出一系列不同尺寸的双锥形截面毛坯，这为研究整体双锥形环件闭式径向辗轧的不均匀塑性变形机理和形性一体化协同调控提供了重要基础。

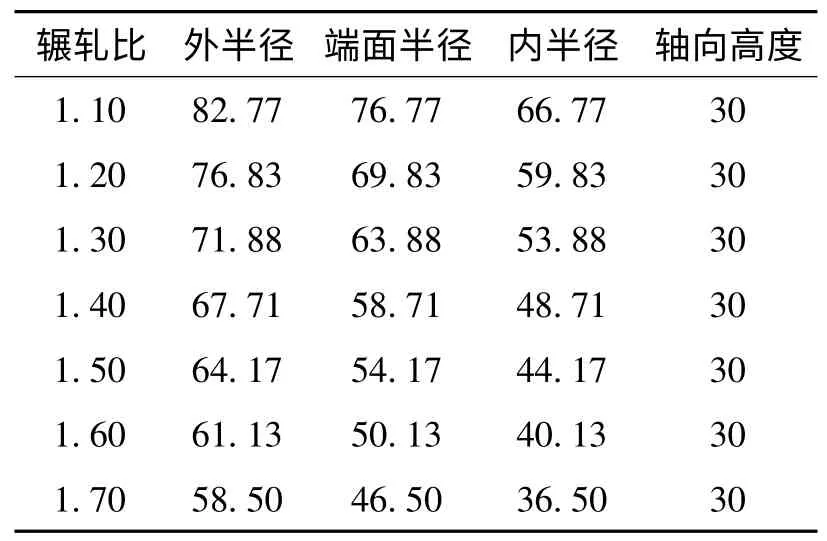
表1 基于不同辗轧比的双锥形截面毛坯尺寸Tab.1 BCSB dimensions based on different rolling ratios mm

最后，将所提出的整体双锥形环件闭式径向辗轧毛坯尺寸设计思想扩展到了其它18 种异形截面环件径向辗轧毛坯尺寸设计中，并通过虚拟辗轧试验验证了其可行性和有效性。在上述研究的基础上，利用C 语言设计和开发一套如图2 所示的异形环件径向辗轧毛坯尺寸设计软件，并已成功获批软件著作权。

图2 异形环件径向辗轧毛坯尺寸设计软件Fig.2 Software of blank dimensions design for radial profile ring rolling

5 结论

针对整体双锥形环件闭式径向辗轧毛坯尺寸设计这一实际问题，利用体积不变原理给出了双锥形截面毛坯尺寸的计算公式，根据稳定成形条件推导了辗轧比的合理取值范围，提出了一种基于辗轧比的毛坯尺寸设计新方法和软件系统，并通过实例验证了所提方法的有效性和可行性。当然还需指出的是，毛坯尺寸设计与工艺参数设计是紧密相关的，只有它们都进行了合理设计且符合辗轧机实际力能参数，才能成形出符合实际的环件产品。

［1］Lanyun Li，He Yang，Lianggang Guo.Hot shape rolling［J］.Comprehensive Materials Processing，2014，5(19):393－439.

［2］Lanyun Li，He Yang，Lianggang Guo，Zhichao Sun.Research on the influences of material properties and forming parameters in T-shaped closed cold ring rolling process International Journal of Materials and Product Technology，2010，38(2－3):323－326.

［3］华林，黄兴高，朱春东.环件轧制理论和技术［M］.北京:机械工业出版社，2001.

［4］华林，钱东升.轴承环轧制成形理论和技术［J］.机械工程学报，2014，50(16):70－76.

［5］Lanyun Li，Xiao Li，Jing Liu，Zhi He.Modeling and simulation of cold rolling process for double groove ball-section ring［J］.International Journal of Advanced Manufacturing Technology，2013，69(5－8):1717－1729.

［6］Lanyun Li，Xiao Li，Zhi He.Research on the effect of geometric parameters of ring blank on cold profiled ring rolling process［J］.International Journal of Materialsand Product Technology，2011，42 (3－ 4):195－208.

［7］Dongsheng Qian，Lin Hua，L.B.Pan.Blank design optimization for T-section ring rolling［J］.Ironmaking＆ Steelmaking，2009，36(6):462－469.

［8］Dongsheng Qian，Lin Hua.Blank design optimization for stepped-section profile ring rolling［J］.Science China Technological Sciences，2010，53(6):1612－1619.

［9］Keeton C R.Ring rolling in Metals handbook:Forming and forging［M］.Metals Park，OH:ASM International，1988.

［10］Kang B S，Kobayashi S.Preform design in ring rolling processes by the three-dimensional finite element method［J］.International Journal of Machine Tools and Manufacture，1991，31(1):139－151.

［11］郭良刚，杨合，金坚诚.环件径轴向轧制毛坯尺寸设计方法［J］.机械工程学报，2010，46(24):1－9.

［12］Lanyun Li，He Yang，Lianggang Guo，Zhichao Sun.A control method of guide rolls in 3D-FE simulation of ring rolling［J］.Journal of Material Processing Technology，2008，205(1－3):99－110.