振动除冰车驾驶员舒适性的优化分析

万义强，黄 华，姜 宏

(北京理工大学 机械与车辆学院，北京100081)

振动除冰车驾驶员舒适性的优化分析

万义强，黄 华，姜 宏

(北京理工大学 机械与车辆学院，北京100081)

以某型振动除冰车为研究对象，建立整车模型，以驾驶员在不同频率下振动除冰作业及高速转场中所受到的垂直振动加速度均方根值为目标函数，对比3种工况下的区别，对驾驶室悬置阻尼进行优化，提出取值方案，以提高驾驶员的舒适性，提高工作效率.

除冰车；阻尼；MATLAB；舒适性

振动除冰车在执行除冰作业时，由振动轮和路面激励所引起的振动会对驾驶员产生一定的影响，使驾驶员舒适性和工作效率降低，甚至对驾驶员的健康产生危害.以某型除冰车为例，以驾驶员脊椎位置的垂直方向的加速度均方根值为目标函数，使用理论计算的方法[1-5]，对比3种工况下加速度均方根值随阻尼比变化的情况，分析得到阻尼比的优化取值方案.

1 除冰车动力学模型

除冰车可简化为图1所示的六自由度平面振动模型[6].

在建立力学模型时做了如下简化：①振动过程中各部分的振动位移都是在其平衡位置附近的微振动；②由于振动除冰车结构上的对称性，左、右两后轮胎接触的路面的统计特性可认为基本相同，将其简化为半车模型；③振动除冰车前机架与后机架间铰接点连接在竖直方向上认为是刚性的；④各级减振元件都具有线性特性，不考虑非线性.

图1中，m1为簧载质量；m2为驾驶室质量；J1为簧载质量俯仰转动惯量；J2为驾驶室俯仰转动惯量；mA为前悬簧下质量；mB为后悬簧下质量；k1为前悬架刚度；k2为后悬架刚度；kw1为前轴车轮刚度；kw2为后轴车轮刚度；c1为前悬架阻尼；c2为后悬架阻尼；cw1为振动轮阻尼；cw2为后轴轮胎阻尼；l为簧载质量质心与驾驶室质心水平距离；l1为簧载质量质心与前悬水平距离；l2为簧载质量质心与后悬水平距离；l3为驾驶室质心与驾驶室前悬置水平距离；l4为驾驶室质心与驾驶室后悬置水平距离；Xc1为簧载质量质心垂直位移；Xc2为驾驶室质心垂直位移；x1为前悬簧下质量垂直位移；x2为后悬簧下质量垂直位移；φ1为簧载质量俯仰角；φ2为驾驶室俯仰角.

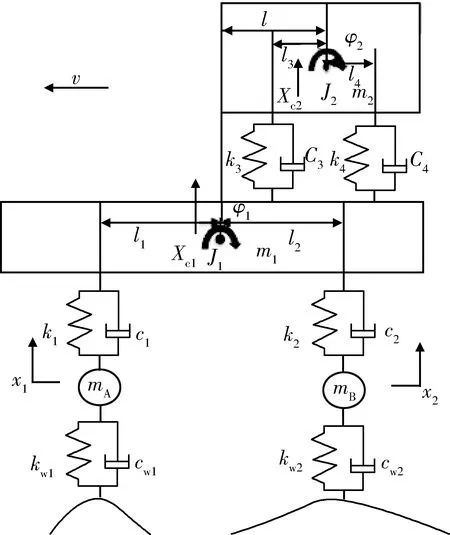
图1 振动除冰车动力学模型

2 整车运动方程的建立和频响函数推导

由所建立的模型，应用拉格朗日方法，建立多自由度系统的运动方程.系统的动能、势能和耗散功分别为

(1)

(2)

(3)

将以上3式代入拉格朗日方程

(4)

Qi为除保守力以外的力.得到动力学方程

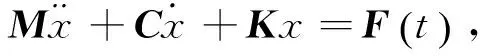
(5)

式中:M、C、K和F(t)分别为系统的质量矩阵、阻尼矩阵、刚度矩阵和激励矩阵.

对上面动力学方程(5)做拉普拉斯变换.

(6)

可求得系统传递函数

(7)

由此推出

(8)

对振动除冰机模型分析，可求出系统振动轮垂直位移q1、驱动轮胎垂直位移q2的两个输入对驾驶员垂直位移Xc2输出的传递函数，并令s=jω，得到相应的频率响应函数

(9)

(10)

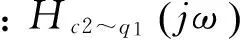
按照线性叠加原理，并利用平稳随机过程的维纳-辛钦公式，可推导出振动除冰机在受到垂直振动轮位移q1和驱动轮胎垂直位移q2两个激励时，驾驶员处垂直响应Xc2的功率谱密度

(11)

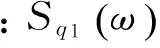
可以推得振动除冰机的力学模型中，驾驶员的垂直振动加速度相应功率谱密度为

(12)

振动轮产生的振动垂直位移q1(t)=Asin(ωt)，振动轮输入谱密度和路面激励谱密度分别为

(13)

(14)

式中：A为振动轮垂直位移幅值；ω0为激振角速度；Sq2(n0)为路面不平度系数；V为车辆行驶速度；n0为参考空间频率.

以下分工况对除冰车的乘坐舒适性考察.

(1)当进行除冰作业时，车辆行驶速度为3 km/h，振动轮工作频率分别为20 Hz和30 Hz，振幅为0.004 m的情况，求得

(15)

(2)当除冰车正常行驶时，其行驶速度为11 km/h，振动轮不进行作业，选取C级路面分析求得

(16)

当在工况(2)时，振动轮与驱动轮胎的路面输入存在一个时间差，公式为

(17)

此时，对路面输入进行傅里叶变化得到

(18)

(19)

由此推导驾驶员的垂直方向的加速度均方根值arms为

(20)

3 计算结果分析

针对除冰车驾驶室悬置，以阻尼比为变量，在3种工况下进行优化，但刚度的取值首先需要确定.通过刚度匹配计算发现，从动行程均方根值变化趋势来分析，前后悬置刚度取值越大越好，但是从加速度均方根值变化趋势来看，却是与之相反的.在刚度选取时应针对不同车型具体分析.通过分析得到如下信息：①加速度随前悬置刚度变化较后悬置刚度变化更为显著；②后悬置动行程随驾驶室悬置刚度变化显著； ③驾驶员脊柱位置动行程随前后悬置刚度变化不明显.

由以上信息得出驾驶室悬置刚度取值方案：前悬置刚度取值尽可能的低且避开车身固有频率，取值为1.8 Hz，再考虑到驾驶室悬置受其布置位置的影响，后悬置取2.4 Hz.

对阻尼比进行优化分析，取驾驶室前后悬置阻尼比相同，分别研究除冰车以不同工作频率进行除冰作业和正常行驶时，以驾驶员脊椎位置的加速度为目标函数，分析其最优阻尼比，得到多种工况下驾驶员脊椎位置加速度均方根值随阻尼比的变化曲线.见图2～图4.

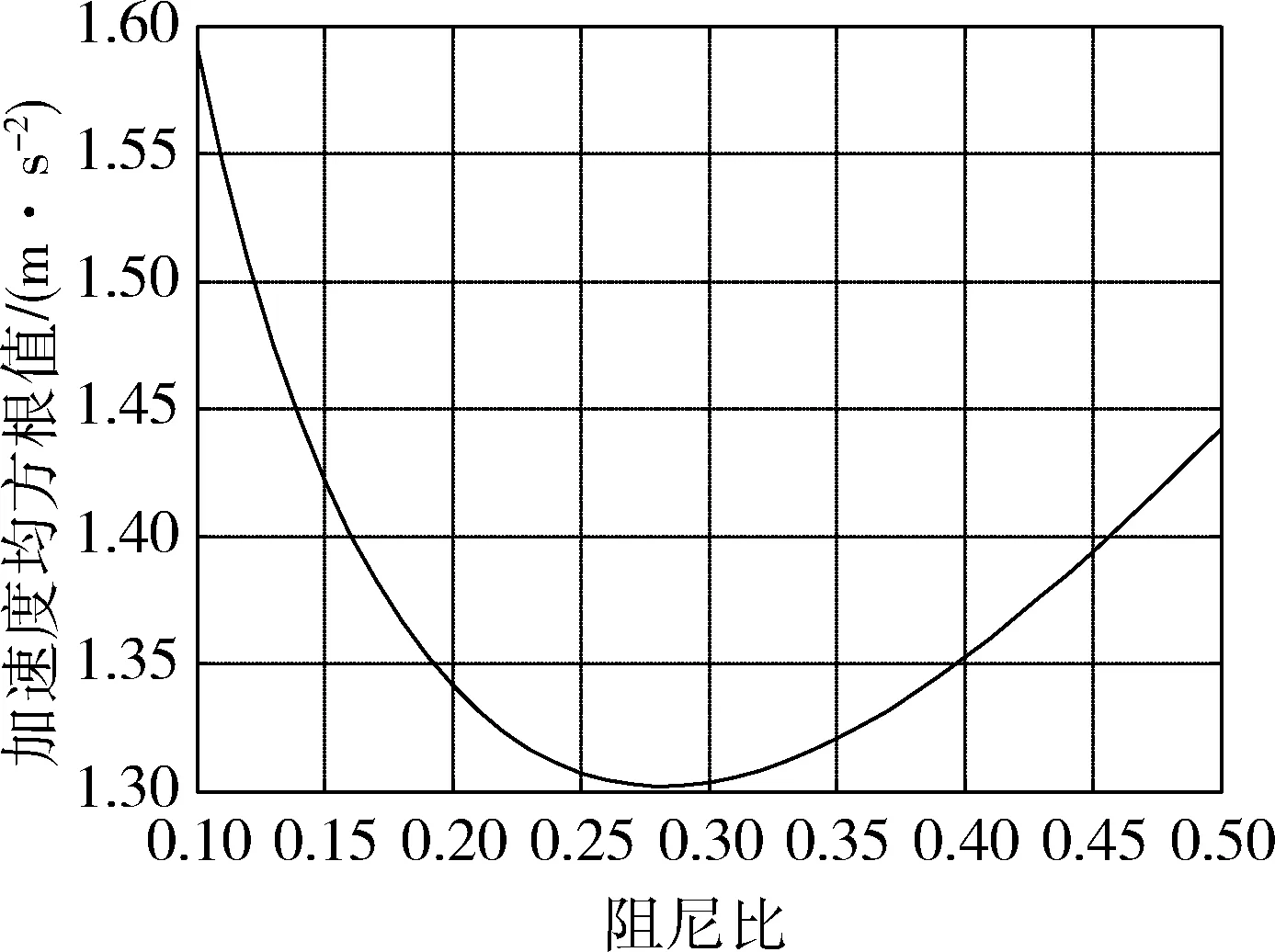
图2 11 km/h正常行驶工况

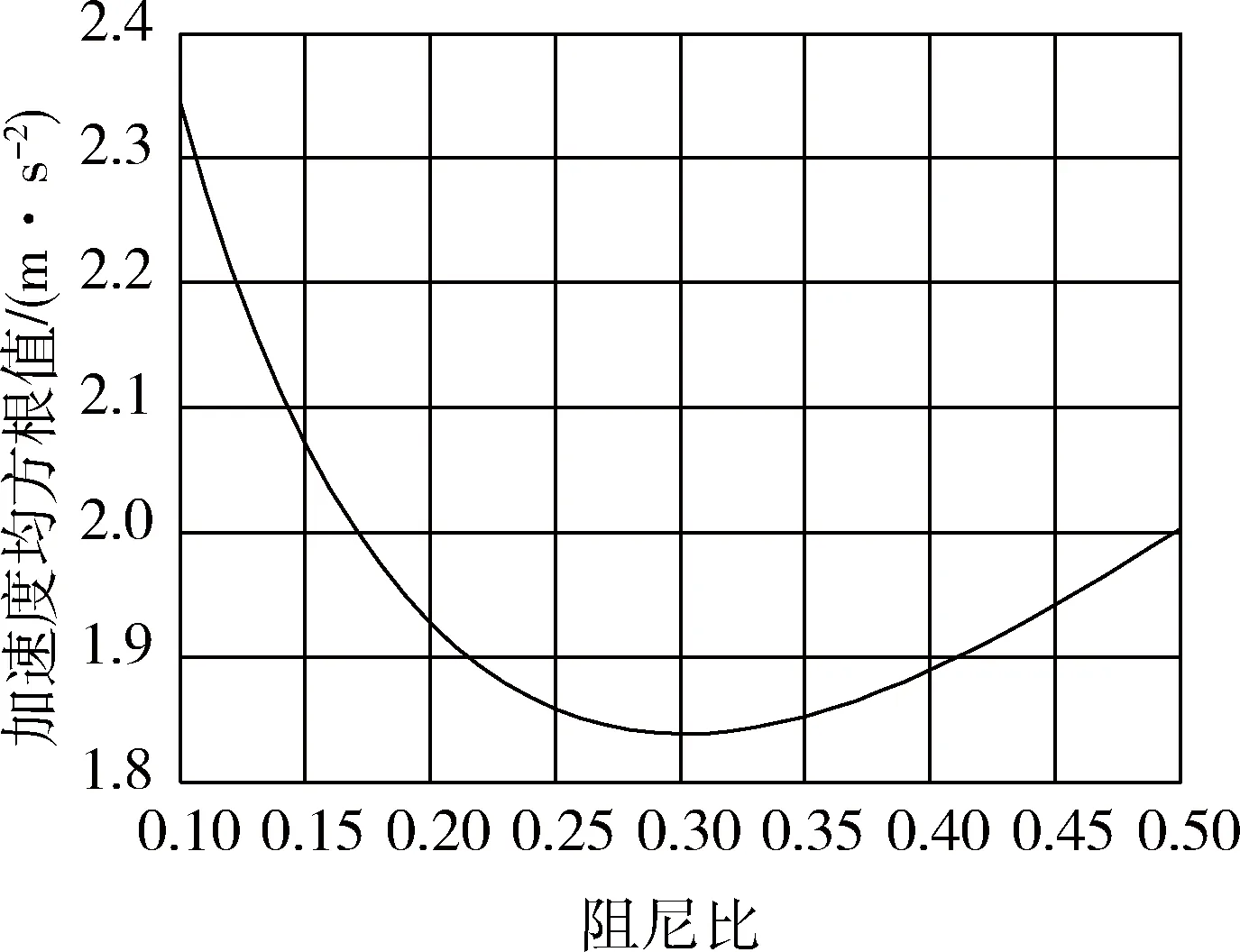
图3 3 km/h速度，激振频率为20 Hz的工况

图4 3 km/h速度，激振频率为30 Hz的工况

由图可见，通过数值仿真结果得到：在11 km/h工况下，当阻尼比为0.28时,驾驶员脊柱位置垂直方向加速度均方根值最小，为1.302 m/s2；3 km/h的速度，20 Hz激振频率的工况下，当阻尼比为0.3时,驾驶员脊柱位置垂直方向加速度均方根值最小，为1.84 m/s2；3 km/h的速度，30 Hz激振频率的工况下，当阻尼比为0.31时,驾驶员脊柱位置垂直方向加速度均方根值最小，为2.068 m/s2.

可见，在转场工况下，驾驶员脊柱位置垂直方向加速度均方根值较小，当除冰车在进行除冰作业时，加速度均方根值较大，且随激励频率的增加而增大,且在不同工况下，其最优阻尼比有差异.

4 结 论

以某型除冰车为例，建立了除冰车数学模型，推导驾驶员脊椎加速度均方根值.通过计算分析得到最佳刚度匹配.对3种工况进行分析，得到不同工况下理想的阻尼比.为保证驾驶员的舒适度和工作效率，应尽量降低驾驶员脊柱位置垂直方向加速度，因此,在除冰车驾驶室悬置的设计中，应选用可调阻尼减震器，根据不同工况对阻尼比进行调整，达到实时对驾驶员舒适度优化的目的.如使用非可调阻尼减震器，应根据其最常用工作工况进行选择，从而使驾驶员长期保持在最优的工作环境中.

[1] 余志生．汽车理论[M]．北京：机械工业出版社，2008．

[2] 秦四成．振动压路机[M]．北京：化学工业出版社，2006．

[3] 刘方文. 某重型卡车驾驶室悬置匹配分析[D]．长春:吉林大学，2005.

[4] Manfred Mitschke, Henning Wallentowitz．汽车动力学[M]．陈萌三,译．北京：清华大学出版社，2009.

[5] 史广奎，李 槟，孟宪民．汽车设计中减震器相对阻尼系数的确定[J]．汽车工程，1995，6(17):367-373.

[6] 徐 琢,李晓雷,吕晓鹏,等．矿车驾驶室悬置刚度匹配计算[J]．装甲兵工程学院学报,2014,28(5):39-44.

Optimization Analysis of Driver’s Comfort of a Vibration Deicing Vehicle

WAN Yi-qiang， HUANG Hua, JIANG Hong

(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081，China)

Taking a certain type of the vibration de-icing vehicle as the research object, the vehicle model is established. The values of root mean square of the vertical vibration acceleration suffered by the driver are taken as the target functions under different working conditions such as the vibration deicing operation at different frequencies and the high-speed driving. Comparing three different working conditions of them, the damping of cab suspension is optimized, and the scheme for the parameter selection is proposed for improving the comfort of the driver.

de-icing vehicle; damping; MATLAB; ride comfort

1009-4687(2015)04-0009-04

2015-1-20

万义强(1989-)，男，硕士.

U461

A