汽车轮毂冲击试验的力学模型研究

张国智

(新乡学院 机电工程学院，新乡 453003)

汽车轮毂冲击试验的力学模型研究

张国智

(新乡学院 机电工程学院，新乡 453003)

研究汽车轮毂冲击试验的解析预测方法.基于曲杆弯曲理论和动静法，建立了汽车轮毂冲击试验轮辐处的最大应力的理论计算模型；通过与有限元计算结果的对比，验证了理论模型的准确性.对比一批汽车轮毂的冲击试验的有限元和理论模型的计算结果，可知，理论模型的准确度与轮辐曲率变化、截面形状复杂程度有关，最大相对误差不超过15%.该研究为汽车轮毂快速优化设计提供了方法和理论依据.

汽车轮毂；冲击试验；曲杆弯曲；动静法；快速优化

随着节能环保汽车的要求，以汽车轮毂为焦点的研究已成为研究热点之一[1]，其中，轮毂的强度性能方面是重点研究要点.在轮毂的强度试验中，轮毂冲击试验是检验轮毂性能的一个重要试验，目的是测试轮毂的抗冲击碰撞能力，该试验的数值模拟是轮毂所有台架试验中最难模拟的一个，它是融合了接触非线性、几何非线性、材料非线性为一体的高度非线性的动态冲击问题，目前，关于该试验的各种数值模拟研究得到了许多学者的关注[2-4]，取得了一定的研究成果.但数值模拟虽然计算精度较高，能够反映轮辐局部的应力分布，但计算效率较低，因而，在轮毂轮辐结构优化设计中应用数值模拟方法严重影响研发的效率，此外，大多数轮毂的危险截面在轮毂的轮辐位置，因而，轮毂轮辐在冲击试验中的最大应力的解析计算的研究十分重要.目前，关于此方面的研究尚不深入、系统，本文基于此，基于曲杆弯曲理论及动静法，对轮毂轮辐在冲击试验中的应力的解析计算模型进行了深入、系统的研究.

1 轮毂冲击试验简介

试验用的轮毂是未经试验或使用的新成品轮毂，试验环境温度为10～38 ℃.试验设备可以将冲击载荷施加到装有轮胎的轮毂的轮辋轮缘上的位置.为了使垂直下落的冲击块能与轮辋的最高点接触，按轮毂轴线与冲击块垂直下落方向成(13±1)°角的方式安装轮毂.冲击块的冲击面长不小于375 mm、宽不小于125 mm.为适应各种规格和形状的轮毂做冲击试验，整个轮毂支架的位置可以调节，如图1所示[5].

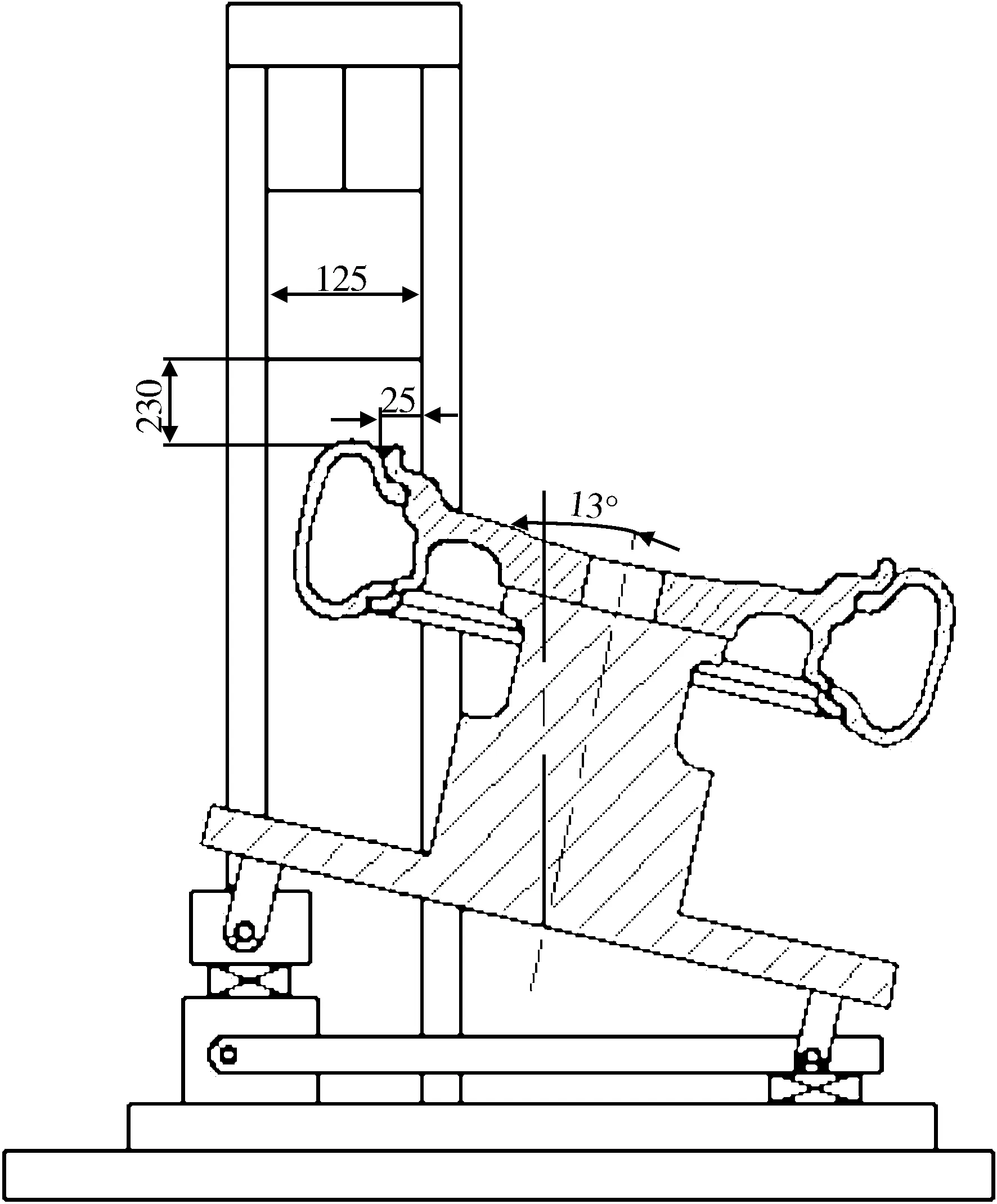
图1 轮毂冲击试验

2 轮毂冲击试验的最大应力的理论模型的建立

2.1 冲击载荷的处理

根据动静法，有

Fd=FstKd，

(1)

式中：Fd为受冲击最大的轮辐所受的冲击载荷;Fst为冲击块的重力;Kd为动载系数.

动载系数为

(2)

式中：h为冲击块的下落高度;Δst为整个台架系统在总的冲击块重力下所产生的静载变形.

Δst=Δst1+Δst2，

(3)

式中：Δst1为橡胶垫的静载变形;Δst2为轮胎的静载变形.

根据理论力学和车辆动力学理论[6]，有

(4)

式中：k1为轮胎的弹性系数;k2为橡胶垫的弹性系数.

2.2 载荷的移置

Fd可分解为沿轮胎法向和与切向的两个力

(5)

式中：Fd1为Fd沿轮胎法向的分力;Fd2为Fd沿轮胎切向的分力.

将Fd1移置支撑架中心O，如图2所示.产生的附加弯矩M为

M=Fd1a/cosα，

(6)

式中：a为冲击块重心距支撑架中心O的水平距离.

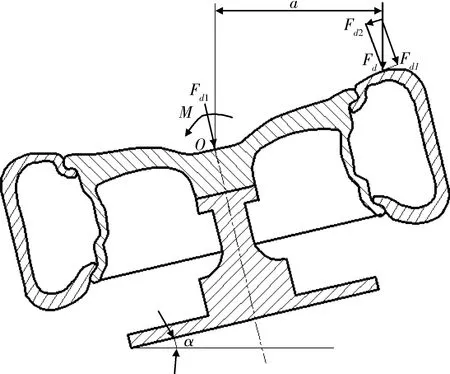
图2 轮毂冲击试验的受力简图

2.3 最大应力的计算

轮毂的受冲击的轮辐在受冲击某个时刻所受到的弯曲应力达到最大，本文将轮毂的轮辐视作压弯组合变形的悬臂梁结构，在计算所受冲击的轮辐所受最大弯矩和压缩力基础上，进一步计算所受冲击轮辐的最大应力.

首先，根据权系数加权法，可近似推得受冲击轮辐的弯矩M′为

(7)

式中：θi为轮毂所有轮辐与冲击对称面间的周向夹角.

其次，根据权系数加权法，可近似推得受冲击轮辐的由切向力引起的压缩载荷F′为

(8)

轮毂冲击试验的危险截面受力如图3所示.在图3中，m-n截面为危险截面，O点为截面的曲率中心，r为中性层曲率半径.根据曲杆弯曲理论，轮毂轮辐危险截面m-n处的最大弯曲应力为

(9)

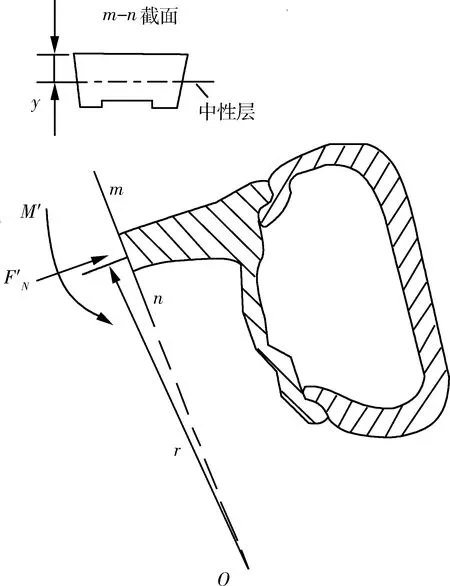
图3 轮毂冲击试验的危险截面受力简图

轮毂轮辐危险截面m-n处的压应力为

(10)

轮毂轮辐危险截面m-n处的综合最大正应力为

σmax=σb+σc.

(11)

根据第四强度理论来判断轮毂是否能通过轮毂的冲击试验，判断准则为：

(12)

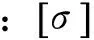
3 理论模型的验证与讨论

以帕萨特轿车的某款铸造铝合金轮毂为例来验证所建立的汽车轮毂冲击试验的理论模型的准确性.在该轮毂冲击试验中，冲击块的质量为540kg，下落高度为230mm，具体的冲击位置如图1所示，所配轮胎型号为P205/55R16，铸造铝合金轮毂所采用的材料是A356，该数值模拟采用双线性各向同性弹塑性材料模型.由于结构及载荷的对称性，只对轮毂的一半进行分析，对称面为对称约束，台架底部固定，对冲击块施加重力加速度为9.8m/s2，约束冲击块旋转自由度，为了缩短计算时间，首先按自由落体计算冲击块下落到220mm的速度为2.077m/s，然后对冲击块施加初速度为2.077m/s，此时，冲击块距轮毂高度为10mm.该轮毂冲击试验的有限元模型如图4所示，该轮毂在冲击瞬间应力达到最大值时刻的等效应力分布如图5所示，最大等效应力出现在冲击块所冲击轮辐的背面，最大等效应力为209MPa，根据文中的理论模型,该轮辐处的计算的结果为221MPa，与有限元的计算结果的相对误差为5.7%，可知，所建立的理论模型与有限元模型是正确的.

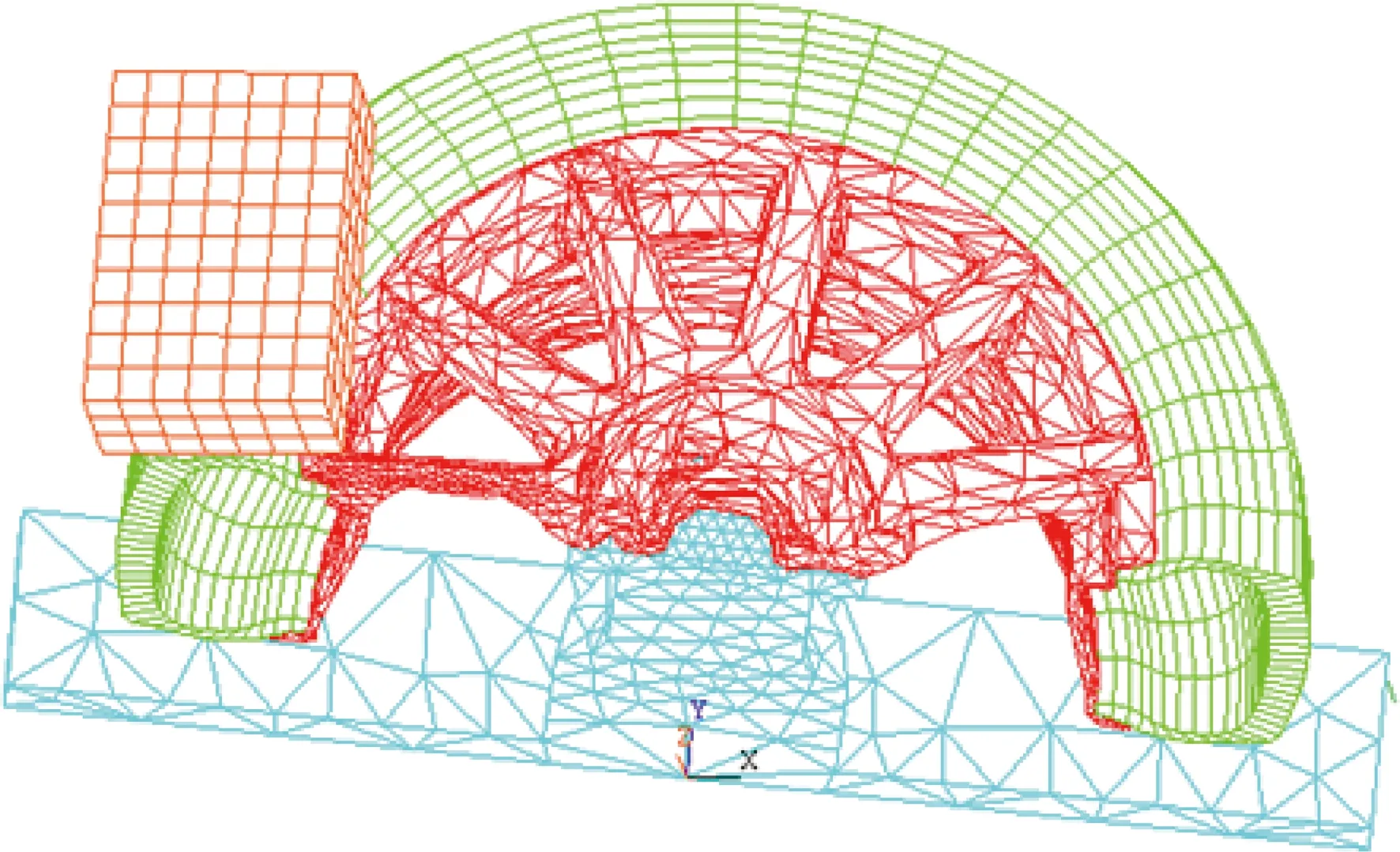
图4 轮毂冲击试验有限元力学模型

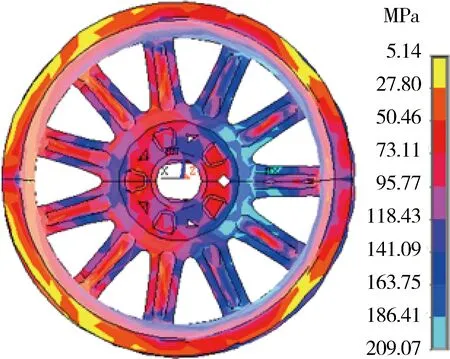
图5 轮毂冲击试验有限元分析的等效应力分布

基于所建立的理论模型，对六款典型的轮毂进行了计算，有限元与理论计算结果如表1所示，从表1中可见，对于轮辐曲率变化小、截面形状简单的轮毂相对误差最小，二者相对误差在7%左右，对于轮辐曲率变化大、截面形状复杂的轮毂的相对误差最大，二者相对误差在15%左右，并且，理论计算结果均略高于有限元计算结果，这主要是由于在理论建模时的简化造成的.

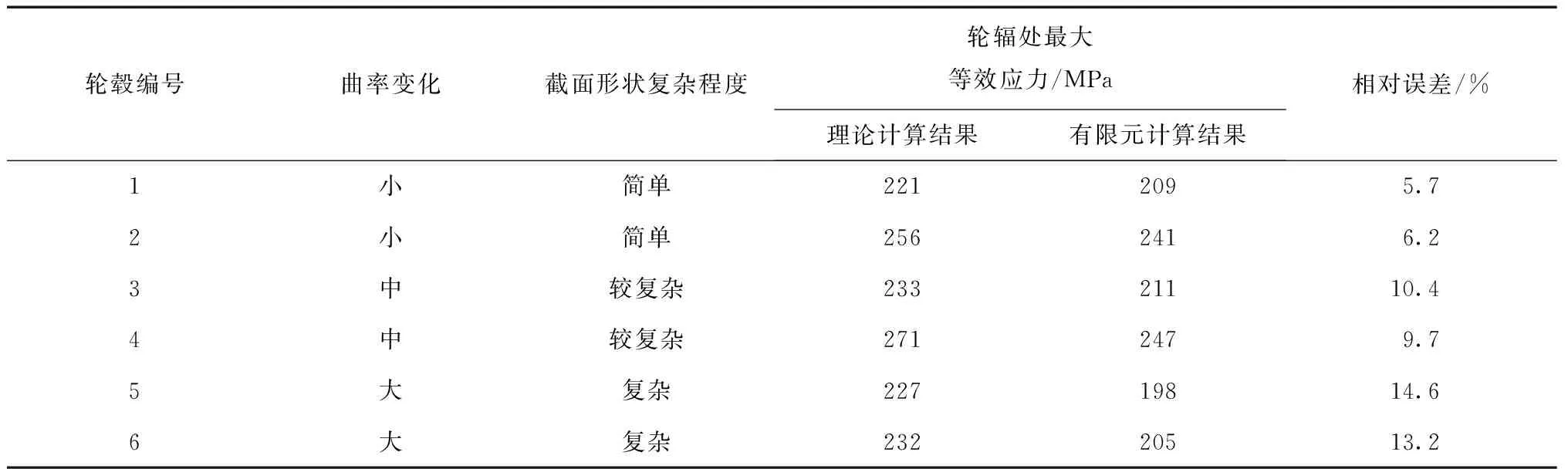
表1 有限元与理论计算结果对比表

4 结 论

1)应用所建立的汽车轮毂冲击试验轮辐处的最大应力的理论模型，对某款轮毂的冲击试验进行了计算，与有限元计算结果的两者误差为5.7%，验证了该理论模型的准确性.

2)通过对一批典型汽车轮毂的计算，与有限元计算结果的最大误差为14.6%，进一步验证了该理论模型的准确性.

3)通过对一批典型汽车轮毂的理论计算与有限元计算结果的对比，可知，所建立的理论模型的计算误差与轮辐曲率变化、截面形状有关，总体而言，所建立的理论模型的准确度基本可满足工程需要.

文中研究为汽车轮毂冲击试验预测方法及快速优化设计提供了分析方法和一定的理论依据.

[1] 车坚志，张 君，胡 波，等. 重载轮式车辆轮毅电机系统方案设计与控制研究[J].车辆与动力技术, 2013(2):39-42.

[2] 臧孟炎, 秦 滔.铝合金车轮13°冲击试验仿真分析[J].机械工程学报,2010,46(2):83-87.

[3] 畅世为, 张维刚. 复合材料车轮冲击试验仿真分析[J]. 汽车工程,2010,32(1):65-68.

[4] 武海滨，闫绍峰，仪登利. 铝合金轮毂的有限元分析[J]. 辽宁工程技术大学学报(自然科学版),2010,29(2):282-284.

[5] 南京汽车研究所, 中信戴卡轮毂制造有限公司. GB/ T15704-1995轿车车轮冲击试验方法[S] . 北京: 中国标准出版社, 1999.

[6] Hans-Peter Willumelt. 车辆动力学模拟及其方法[M].北京:北京理工大学出版社,1998.

Study on Mechanical Model of Impact Test of Vehicle Wheels

ZHANG Guo-zhi

(Mechanical and Electrical Engineering College，Xinxiang University， Xinxiang 453003， China)

An Analytical prediction method for the impact test of vehicle wheels was studied. Based on both the Bending Theory for curved bars and the Dynamic Static Method, a theoretical calculation model of the maximum stress at the spokes of the wheel was established in the impact test. The FEA results from testing a batch of automobile wheel hubs were compared with those from the theoretical model, and the model was verified. The accuracy of the model was related with the changes of the spoke curvature and the shapes of its cross-section. The maximum relative error did not exceed 15%. The study provided an analysis method and theoretical basis for rapid optimization of the vehicle wheels.

vehicle wheels; Impact test; bending theory of curved bars; dynamic static method; rapid optimization

1009-4687(2015)04-0003-04

2015-3-13

河南省教育厅自然科学研究计划项目(2011C460002)

张国智(1978-)，男，博士，副教授,研究方向为有限元数值模拟、工程中的优化方法、宏微观塑性力学、生物力学等.

TH12

A