激光红外大气传输透过率模型研究
2015-04-03陈芳芳
陈芳芳,耿 蕊,吕 勇
激光红外大气传输透过率模型研究
陈芳芳,耿 蕊,吕 勇
(北京信息科技大学 仪器科学与光电工程学院,北京 100192)
为了提高激光红外传输在工程应用方面的精度,以辐射传输理论为基础,考虑大气湿度、温度、能见度等容易测量的因素,建立了大气透过率衰减的简化模型。利用模型,对不同波长的激光在各种大气环境及传输路径下的透过率进行了计算,并与商用软件的计算结果进行对比。实验结果表明:简化模型减小了运算量;晴朗大气,简化模型与软件计算结果在特定波段比较接近,最小相对误差低至0.005%。
大气透过率;激光红外;大气分子;气溶胶;吸收系数;PcModWin
0 引言
在激光测距、激光遥感、激光制导和激光传输等方面都必须考虑大气对激光的衰减影响,因此使用影响激光透过率的容易测量的参数,建立简单易懂的激光衰减模型,准确、快速地得到大气的透过率是十分必要的。大气对激光传输的影响主要有2个方面:一是大气衰减使激光传输信号减弱;二是大气分子、气溶胶及悬浮微粒的散射形成背景辐射[1]。由于影响激光传输的因素是多样的,如大气分子、气溶胶、悬浮微粒、云雨雾霾、风、水汽以及海拔等[2],在一定程度上增加了研究透过率的难度。
影响激光衰减的微观因素包括大气分子吸收和散射、大气气溶胶吸收和散射,宏观因素包括大气压强、温湿度、能见度及各种气象条件。从微观大气因素出发计算透过率虽然精度高,但是计算量大,过程复杂,可实现性差。本文把影响透过率的微观因素和宏观因素相结合,以实际测量数据为基础,拟合出最为接近的关系式[3]。
1 大气透过率的理论基础
大气中包含多种气体,氮气占单位体积的78%,氧气占21%,此外,还包含甲烷(CH4)、一氧化二氮(N2O)和一氧化碳(CO)、二氧化碳(CO2)、水汽(H2O)和稀有气体等微量气体。另外大气中还有悬浮的尘埃、液滴、冰晶等固体或液体微粒,这些粒子通常称为气溶胶。
影响激光透过率的因素主要有3个:一是大气中某些气体分子(H2O、CO2等)的吸收;二是气溶胶的散射;三是由气象条件(雨雪等)造成的衰减[4]。吸收、散射和气象条件的影响虽然机理不同,其作用结果均使辐射功率在传输过程中发生了衰减[5]。传输过程中用()表示透过率,用()表示消光系数。
由朗伯-比尔定律知,激光通过大气的透过率可表达为[6]:
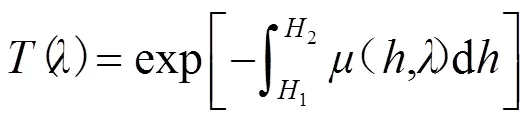
式中:为距离变量;1和2分别为发射激光的起点和终点高度。
若斜程传输,天顶角不大,上式可改写为:
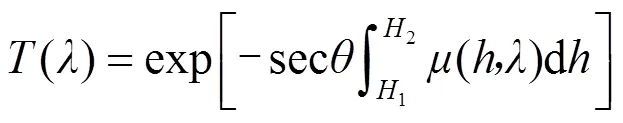
可以用透过率来衡量大气分子、气溶胶和气象条件对激光的衰减,总的大气透射率可表示为:
()=a()×s()×w() (3)
式中:a()为大气分子吸收引起的衰减;s()为气溶胶散射引起的衰减;w()为气象制约引起的衰减。
1.1 大气分子吸收衰减
对于a(),空气中除了水蒸气和CO2,O2和CH4等气体也吸收激光,但其含量少,仅在传输较远时,吸收才稍微明显[2]。O3的吸收能力虽然较强,但是在20km以下的海拔,O3的吸收是非常小的,相对于水蒸气和CO2气体,可忽略不计。因此,主要考虑水蒸气和CO2气体,即:
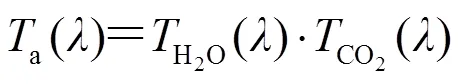
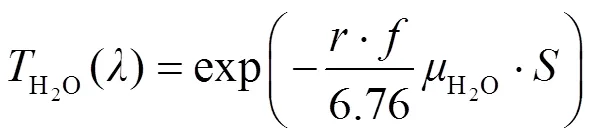
式中:为相对湿度;为(℃)时饱和空气中的水蒸汽质量;为传输距离。当海拔升高到12km以上,大气中水蒸气的含量很少,水的衰减可忽略不计[8]。
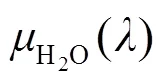
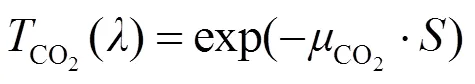
以上公式仅用于海平面水平路程,实际激光的传输路径通常为斜程,因而需要将斜程换算成海平面的等效水平路程。斜程传输距离的海平面水平等效路程可由下式计算[4]:
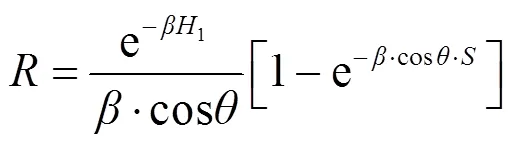
式中:1为激光发射高度,km;考虑水蒸汽时,=0.0654,二氧化碳时,=0.19。由公式(7)可知,只要知道斜程传输的天顶角以及激光发射高度1便可计算出的海平面水平等效路程。所以大气分子吸收可表示为:

1.2 气溶胶衰减
气溶胶对激光的衰减主要由悬浮微粒和气溶胶等的散射造成,与能见度密切相关。常用的描述公式为:
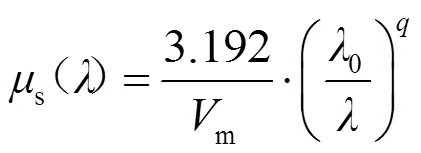
式中:0为可见光波段的波长,一般取0.55μm或0.61μm,因为此波段没有影响大气透过率的吸收,只有散射[7],本文取0.55μm;m为能见度,km;(mm)为激光波长,为与m有关的经验常数,满足条件:

所以气溶胶衰减的透过率为:
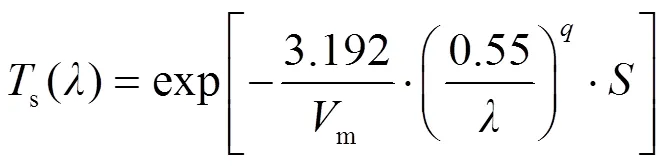
1.3 气象条件引起的衰减
主要考虑雨引起的大气衰减。由于Mie散射理论计算雨滴消光系数比较复杂,实际应用中通常用降雨强度r(mm/h)来估算雨滴对激光的衰减系数,经验公式为[10]:

由此可得由气象衰减透过率:
w=exp(-0.365r0.63×) (13)
1.4 大气透过率的计算
根据上述分析,将公式(8)、(11)、(13)代入公式(3),即可计算温度为(℃)、相对湿度为、降雨强度为r的气象条件下的激光斜程传输大气透过率():
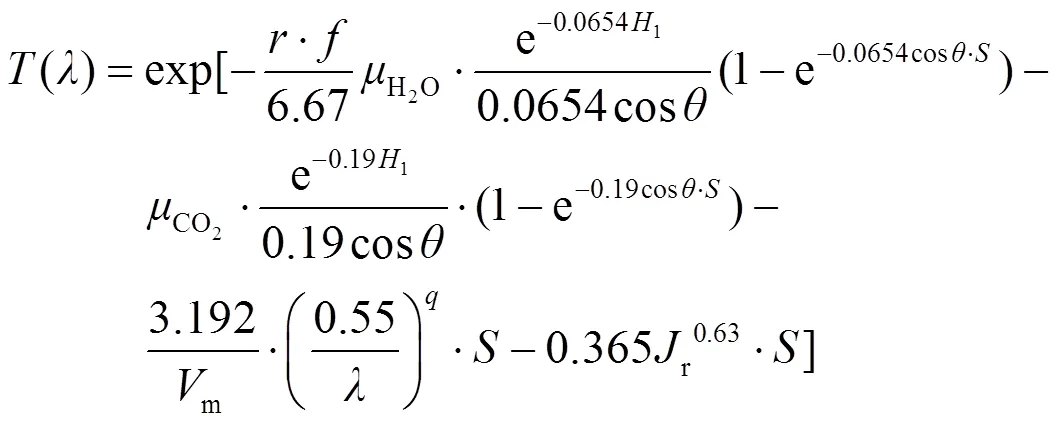
传输距离较小时(<10km),不考虑能见度、相对湿度、大气压强等随高度的变化。
2 仿真实验
计算大气传输透过率的软件主要有LOWTRAN、MODTRAN、PcModWin、FASCODE等。其中,PcModWin是计算透过率比较成熟的软件。该软件是美国空军地球物理实验室开发的,包含了LOWTRAN7低等分辨率和MODTRAN中等分辨率2种模式,能计算在不同气象条件、不同地理位置,不同波长等条件下的透过率[11]。其输入参数既可以是模型本身自带的参数(大气分子含量为默认值),也可以手动输入大气成分(包括大气中各种气体含量)[12]。本文采用PcModWin软件对0.3~13.9μm波段的激光大气传输透过率进行计算,并将计算结果与简化模型的计算结果进行对比分析,以验证简化模型在实际应用中的适用性和有效性。
2.1 晴朗大气情况
晴朗大气情况,降雨强度r=0mm/h,温度、相对湿度、传输距离以及能见度都会对激光大气透过率产生影响。图1、图2分别给出了=10℃、=40%条件下,激光在不同能见度的晴朗大气中传输2km、10km后的透过率随激光波长的变化曲线。
波长5~8μm的激光在大气中传输时透过率几乎为0,因此这一波段一般不被激光传输应用所采用,以下仅讨论3~5μm和8~12μm两个大气窗口内的透过率计算对比分析。
从图1可以看出,传输距离2km时,两种方法计算的透过率结果在窗口内波长为3.5~4.3μm、8.4~11.9μm的范围内都比较接近,相对误差较小。其中,水平传输的最大、最小相对误差为5.699%和0.420%,分别出现在11.8μm和8.6μm波长;斜程传输的最大、最小相对误差下降为5.001%和0.240%,出现的波长略有偏移,变为10.7μm和8.6μm。传输距离10km时,规律与2km一致,水平、斜程传输时的最大、最小相对误差变为8.067%(10.9μm)、0.521%(9.8μm)、7.342%(10.7μm)和0.315%(9.2μm)。
由图2可知,传输2km时,水平、斜程传输时的最大、最小相对误差变为4.108%(11.5μm)、0.209%(9.0μm)、3.865%(9.8μm)和0.005%(10.6μm)。传输距离10km时,水平、斜程传输时的最大、最小相对误差变为7.061%(10.8μm)、0.104%(9.8μm)、6.793%(11.5μm)和0.075%(11.9μm)。
图3、图4分别给出了=20℃、=40%条件下,激光在不同能见度的晴朗大气中传输2km、10km后的透过率随激光波长的变化曲线。
由图3可知,传输2km时,水平、斜程传输时的最大、最小相对误差变为6.321%(8.8μm)、0.455%(11.5μm)、5.071%(10.8μm)和0.136%(9.7μm)。传输距离10km时,水平、斜程传输时的最大、最小相对误差变为7.4814%(9.7μm)、0.679%(10.5μm)、6.041%(10.1μm)和0.206%(11.1μm)。
图4能看出,传输2km时,水平、斜程传输时的最大、最小相对误差变为5.607%(9.9μm)、0.339%(11.8μm)、4.371%(10.8μm)和0.037%(9.1μm)。传输距离10km时,水平、斜程传输时的最大、最小相对误差变为7.4814%(9.7μm)、0.679%(10.5μm)、7.623%(11.0μm)和0.409%(8.8μm)。
2.2 降雨天气
相对于激光的波长,雨滴是大粒子,雨的衰减与激光波长无关。雨作为气体分子存在时,水汽含量会随降雨强度不同而有所变化。雨的衰减不仅表现为雨滴的散射和吸收,同时由于降水引起水汽含量增加,水汽的吸收和雨滴的散射加剧了激光在雨中传输的衰减[13]。
图5给出了降雨强度r=2mm/h,能见度0.615km时激光传输0.5km后的透过率随激光波长的变化曲线。
图5可以看出,两种方法的透过率计算结果在3.5~4.9μm、8.0~10.0μm和11.0~12.0μm波长的透过率较为接近,其中4.0μm透过率相对误差最小,仅为0.751%,11.1μm时,相对误差最大,为34.797%,并且整体的透过率较低。
3 结果和讨论
第2节的仿真结果表明:晴朗大气,天气情况、能见度相同时,简化模型对斜程传输的计算结果比水平传输更接近商用软件的计算值。传输2km,能见度为4.615km时,斜程传输相对误差的最大最小值分别小于水平传输(见表1),其他能见度和传输距离,也是如此。而实际的激光大气传输多为斜程传输,因此,此模型比较适用于工程应用。
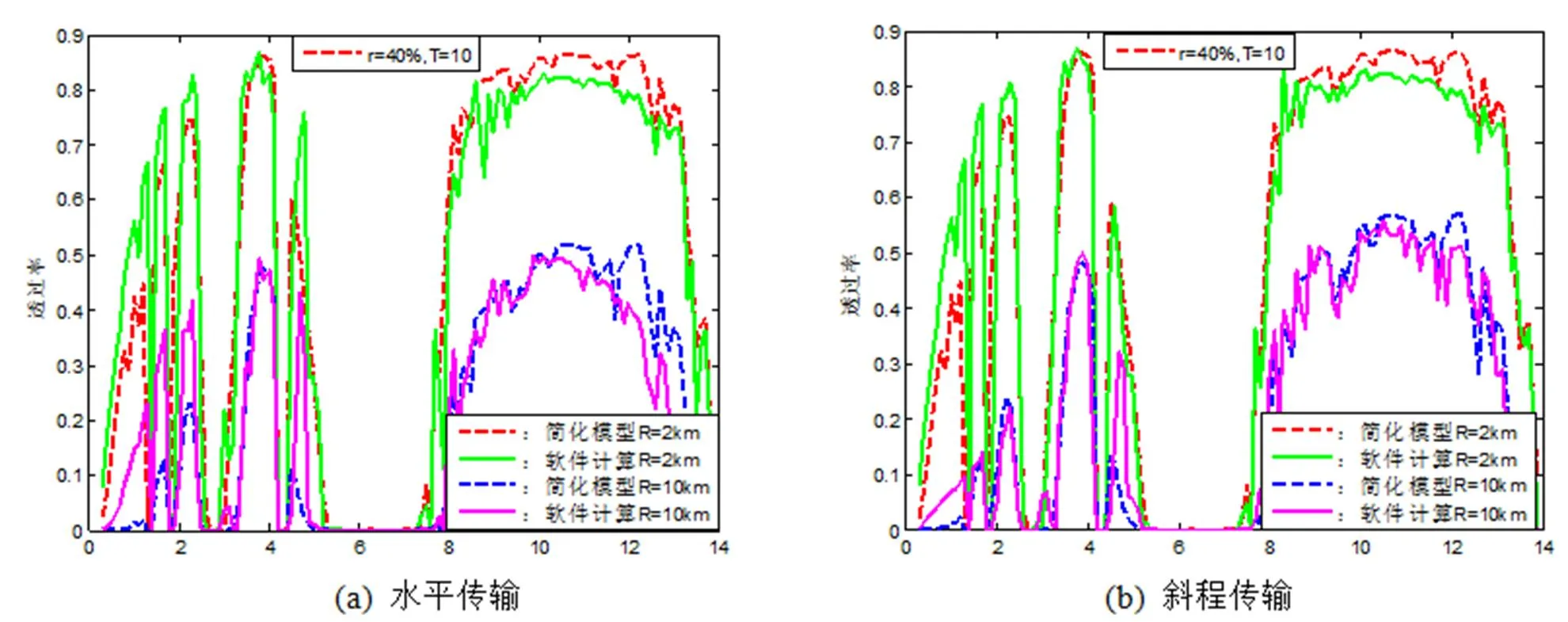
图1 能见度4.615km时,透过率随波长的变化
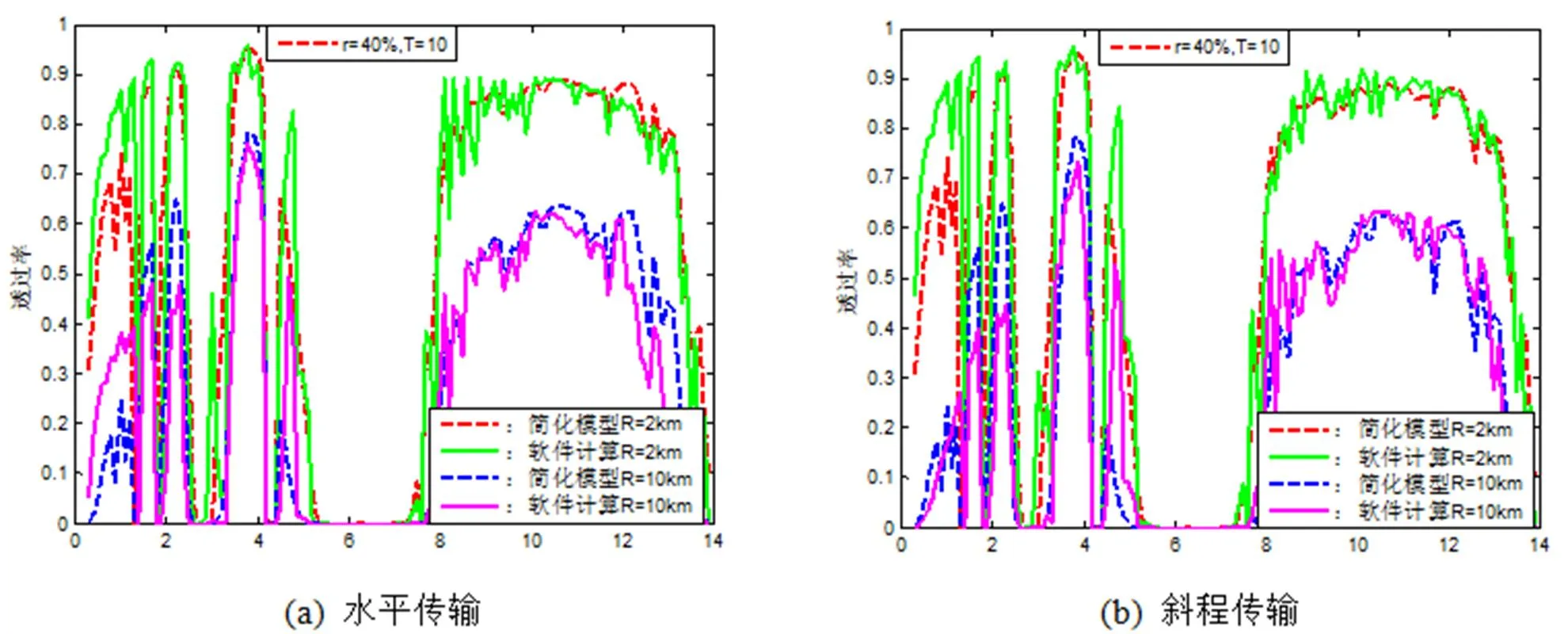
图2 能见度17.692km时,透过率随波长的变化
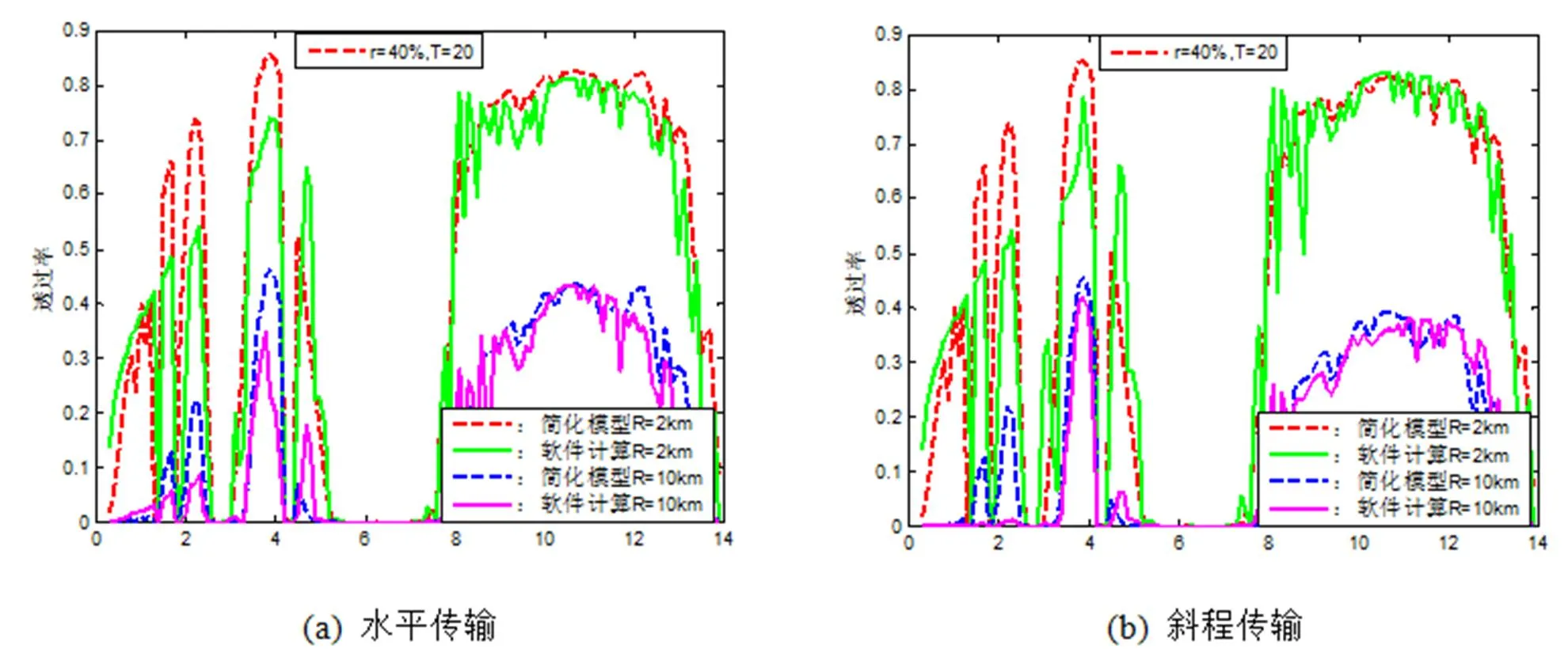
图3 能见度4.615km时,透过率随波长的变化
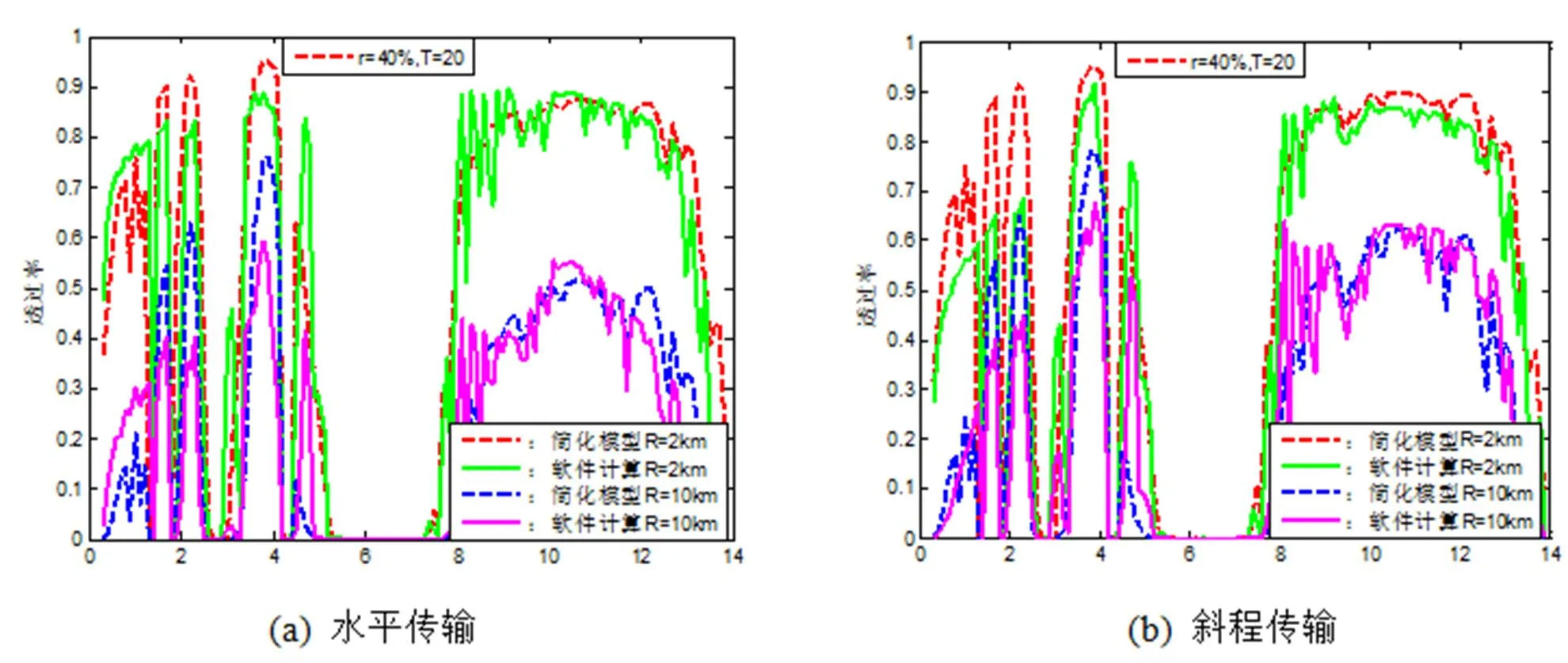
图4 能见度17.692km时,透过率随波长的变化

表1 不同能见度、传输距离、天气情况的相对误差情况

图5 降雨天气透过率随波长的变化
同时,我们也可以看出天气情况和传输条件都相同时,能见度的大小也对简化模型的透过率计算也有所影响。相同传输距离,能见度越大,简化模型与软件计算结果越接近。以=10℃、=40%、斜程传输2km为例,当能见度从4.615km(图1(b))增大到17.692km(图2(b))时,简化模型与软件计算的最小相对误差从0.240%降到了0.005%,其他传输距离的相同传输路径也可得到同样的结论。
对于有降雨的天气情况,简化模型和软件的计算结果差别有所增大,降雨对透过率影响较大,简化模型的适用性变差。这主要是由于软件是用不同类型的云模拟降雨,而云对激光光束的影响随云型和地理位置的不同而有一定的差异,即使相同云型,云的厚度和不均匀性对衰减系数也有影响,而简化模型,仅用降雨量表现雨滴的衰减,忽视了不同地区与气候降雨类型的差别,因此计算结果和软件之间的相对误差较大。实际上,降雨天气即使传输距离很短,激光大气传输的透过率也很低,基本不被工程实验所采用。
4 结论
本文首先研究大气透过率原理,对影响激光传输的因素进行分析,建立了简化透过率模型。然后对比了简化模型与商用软件PcModWin大气透过率计算结果的相对误差。利用本方法,只要知道了温度、湿度、能见度、降水强度等简单的大气数据,就可以计算出红外辐射通过任意路程时的大气光谱透射比。对于精度要求不高的工程计算,具有较好的使用价值。
[1] 刘丹丹, 黄印博, 魏合理, 等. 我国典型地区大气透过率的计算分析[J]. 大气与环境光学学报, 2013(4): 262-270.
[2] 毛克彪, 覃志豪. 大气辐射传输模型及MODTRAN中透过率计算[J]. 测绘与空间地理信息, 2004(4): 1-3.
[3] 贾建周, 宋德安, 贾仁耀, 等. 激光大气传输衰减的估算方法[J]. 电子信息对抗技术, 2010(4): 73-81.
[4] 周国辉, 刘湘伟, 徐记伟. 一种计算红外辐射大气透过率的数学模型[J]. 红外技术, 2008, 30(6): 331-334.
[5] 钱昂, 何友金,刘亮. 反舰导弹中波与长波红外成像制导优势对比研究[J]. 红外技术, 2014, 36(8): 671-675.
[6] 姚庆良. 双基地激光雷达系统原理研究[D]. 西安: 西安电子科技大学, 2008.
[7] Chen S, Sun J, Liu J. Simplified algorithm research of infrared radiation transmission through atmosphere[C]//, 2009, 7494: 74940H(doi:10.1117/12.831341).
[8] Chen S, Sun J-Y. A simplified algorithm to the atmospheric transmi- ttance[C]//2009, 2009: 1-4.
[9] 路远, 凌永顺. 红外辐射大气透射比的简易计算. 红外技术, 2003, 25(5): 9-45, 53.
[10] 王丽黎, 柯熙政, 席晓莉. 激光在雨中传输的分析与计算[J]. 光散射学报, 2005(2): 148-153.
[11] 顾吉林. 典型天气大气辐射传输特性研究[D]. 大连: 大连海事大学, 2012.
[12] 文军, 王介民, 何淑杰. 辐射传输PCModWin程序及应用前景评述[J]. 遥感技术与应用, 1997(4): 47-53.
[13] 魏合理, 刘庆红, 宋正方, 等. 红外辐射在雨中的衰减[J]. 红外与毫米波学报, 1997(6): 19-25.
Research on the Transmittance Model of Laser Infrared Atmospheric Transmission
CHEN Fang-fang,GENG Rui,LYU Yong
(,,100192,)
In order to improve the precision of laser infrared transmission in engineering applications, the integrative theoretic model for the transmittance attenuation model was established based on the infrared radiation transmission theory,and various easily measured factors considered, such as the air humidity, temperature and visibility. In the simplified model, the transmittance of laser, which has different wavelengths, was calculated in a variety of atmospheric and transmission paths, then compared with the results of commercial software. The experimental results show that the model can reduce the amount of computation. In the clear air, the calculations of simplified model are close to the software in a particular waveband, and the minimum relative error is as low as 0.005%.
atmospheric transmittance,laser infrared,atmospheric molecules,aerosol,absorption coefficient,PcModWin
TN21
A
1001-8891(2015)06-0496-06
2014-12-20;
2014-03-16.
陈芳芳(1991-),女,硕士,主要从事激光大气传输方面的研究。E-mail:744409154@qq.com。
北京市教委科研计划项目,编号:KM201511232005。
