基于PSF估计的电阻阵列非均匀性测试

苏德伦，廖守亿，张金生



基于PSF估计的电阻阵列非均匀性测试

苏德伦1,2，廖守亿1，张金生1

（1.第二炮兵工程大学，陕西 西安 710025；2.解放军96111部队，陕西 韩城 715400）

电阻阵列的非均匀性是一种固定模式的空间噪声，是影响红外图像质量的主要因素。测试数据的准确性对非均匀性校正效果是至关重要的，全屏测试时辐射能量的扩散是导致测试误差的重要原因。分析了经典图像复原方法的局限性，提出一种新的基于PSF粗估计的迭代测试方法。分析了不同PSF估计误差对新方法收敛速度和测试精度的影响，评估了不同PSF条件下的测试效果。数值仿真结果表明，新的方法计算量更低，收敛速度更快，且能够适应更宽的平滑因子参数范围。新方法可有效地从退化图像中复原电阻阵列的实际非均匀性图像，取得较好的校正效果。

电阻阵列；非均匀性测试；PSF估计；退化图像复原

0 引言

电阻阵列是一种出射式动态红外景象投射器，它由大规模辐射像元排列组成。每个辐射像元由控制电路和发热电阻组成，通过控制电流的大小来调节发热电阻的温度，从而实现红外辐射成像[1-2]。电阻阵列具有较宽的温度范围和辐射光谱（可用于中波红外和长波红外两个波段），通过提高功率可设计高达200Hz以上帧频，通过真空封装器件极大地减少了热传导实现低串扰。这些特性使得电阻阵列可以生成高质量的红外图像，用于红外成像设备的半实物仿真；并且，电阻阵列为自身发热的出射式器件，不需要光源照射，因而更适合于需要转台安装的动态仿真系统。这使得电阻阵列技术成为目前红外景象生成领域中最受青睐的一种技术。目前中科院上海技术物理研究所已研制成功256×256电阻阵列，目前正在开展512×512电阻阵列的研制工作[3]。

电阻阵列的一个主要用途是在红外成像半实物仿真与测试系统中作为红外图像信号源。因此，输出红外辐射图像的质量成为考核电阻阵列性能的一个重要指标。在理想情况下，对电阻阵列的辐射像元输入相同的控制信号应该输出相同的红外辐射能量。但实际情况是：对于均匀的输入，电阻阵列无法输出均匀的红外辐射图像[4]，这就是电阻阵列的非均匀性。电阻阵列非均匀性的本质是辐射像元输入输出特性的不一致性，其根本原因在于电阻阵列的材料、工艺和结构。从输出红外辐射图像的角度上看，电阻阵列的非均匀性表现为一种固定模式图像噪声。目前，由于非均匀性导致的图像噪声已经成为影响电阻阵列成像质量的主要原因之一[5]。

为了补偿非均匀性引入的图像噪声，目前有效的方法是对输入数据进行校正[6-7]。这种非均匀性校正方法是基于非均匀性测试数据的在线实时校正算法，其校正效果依赖于测试数据的精度。可以说，非均匀性校正的关键即在于对非均匀性信息的准确获取。在前面的研究中，在1:1映射比例前提下，用高斯点扩散函数（point spread function, PSF）描述光学退化模型；提出了一种基于迭代测试的盲复原方法，克服图像退化所引起的模糊效应对电阻阵列非均匀性测试的影响。该方法在PSF平滑因子较小的情况下，通过多次迭代收敛可取得较好的测试效果。但当平滑因子较大的时候，迭代收敛速度变慢并无法收敛到较高的测试精度，因此具有一定的局限性[8]。本文以前文研究为基础，假设实现1:1的映射比例和精确的像元对准，提出基于PSF估计的方法，解决PSF的平滑因子较大时，迭代方法收敛的局限性问题。

1 图像退化对非均匀性测试的影响

在前文[8-9]的研究中详细地论述了电阻阵列非均匀性校正的思路和方法，并分析了测试数据对校正效果的重要作用，此处不再赘述。采用全屏驱动进行非均匀性测试，一是为了提高信噪比，降低环境辐射对测试的影响；二是为了提高测试效率，通过几次迭代测试完成一个驱动等级下所有辐射像元输出测试。

而这种测试采用的是成像探测的方法来实现，电阻阵列辐射像元的输出经过光学系统投射到探测器成像平面，通过采集到的图像数据来分析得出辐射像元的输出。理想的光学系统总是很难实现的，即便实现了完美的透镜系统，对于不同颜色的光其焦距也是不同的。因此，我们所关注的中波（3～5mm）或长波（8～12mm）红外辐射通过光学系统时总会产生退化现象，表现为成像面上的能量弥散。这种能量弥散使得相邻辐射像元在探测平面上形成的光斑互相重叠，从而影响了测试精度。

退化对测试的影响如图1所示。

图像退化平滑了电阻阵列的非均匀性噪声数据，给测量结果带来极大的误差。

图1 图像退化对全屏测试的影响

2 基于PSF估计的非均匀性测试

全屏测试中图像退化的模糊程度由系统的PSF决定，对于退化图像的复原最有效的方法莫过于获知系统的PSF。实际上，对于电阻阵列非均匀性测试系统，当像元映射比例为1:1并达到精确对准时，系统的PSF函数可采用试验估计法，通过点亮一个像元成像，采集系统的单位冲击响应来获取[10-11]。

2.1 经典图像复原的局限性

一旦获知系统的PSF，那么最简单的方法就是利用逆滤波的方法来恢复模糊测试图像。已知系统的退化模型如式(1)所示：

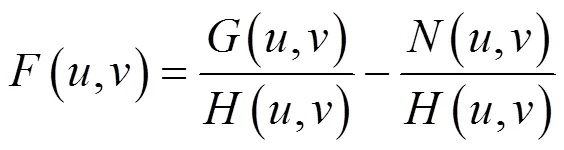
(,)是个低通函数，在高频区域½(,)½趋于0。而系统又不可避免地存在观测噪声项(,)，当存在高频噪声时，将会放大噪声对复原图像的影响[12]。所以逆滤波并不是一个可靠的复原算法。

维纳滤波法是基于最小方差滤波的图像复原方法，它不易受红外成像探测器观测噪声的影响。维纳滤波的另外一个优点在于不需要进行迭代测试，可以对单帧图像滤波复原真实投射图像。但在应用中存在2个问题：

一个是维纳滤波的效果严重依赖于PSF的估计精度，PSF估计误差会严重影响复原效果。而在试验法PSF估计中，单辐射元驱动产生的单位冲击响应图像不可避免地存在环境和设备噪声，所以很难获得精确的PSF估计值。图2所示为存在5%的PSF估计误差时维纳滤波的校正效果。

另外一个问题是边缘效应，由于能量弥散，投射图像边缘的行列辐射能量部分扩散到观测图像范围外，导致信息丢失。在数据处理时需要将采样图像数据(,)转换为频域数据(,)，然后将计算的复原图像的频域值(,)转换为空域值(,)。在(,)®(,)计算中，需要完整的成像数据，但由于辐射能量的分散，实际成像区域大于采样区域，(,)数据的丢失导致边缘效应的出现，如图3所示。要获得完整的(,)数据，要求成像探测器尺寸大于电阻阵列尺寸，或通过二维平移台分别对不同区域进行成像采样，但这些措施都增加了测试系统的复杂性，限制了其实用性。

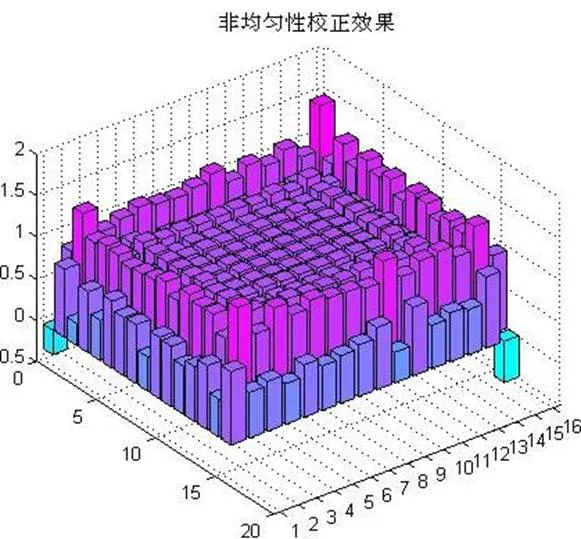
图3 成像观测数据不完整的边缘效应

2.2 基于PSF粗估计的迭代测试复原

综上所述，经典图像复原方法在电阻阵列非均匀性测试中存在诸多问题。为了克服这些不足，采用一种基于PSF粗估计的迭代测试方法，工作流程如图4所示。

首先通过单个辐射像元驱动响应图像获取系统的PSF粗略估计¢。测试的输入图像为某一测试点下的均匀图像数据，电阻阵列的非均匀性表示为加性固定空间噪声信号，认为整个测试系统在1:1映射比例下达到精确的像元对准，那么电阻阵列输出的投射图像为：

＝in＋np(2)

非均匀性信息可表示为：

np＝－in＝D(3)

为提取非均匀性信息需要对探测图像进行如下处理：

D＝－inÄ¢＝Ä－inÄ¢≈DÄ(4)

×＝－(5)

式中：为单位算子；为剩余算子。

图4 基于PSF粗估计的迭代测试

根据式(3)和式(4)有：

D＝(D)＝D－D(6)

当算子的选取使剩余算子很小时，D将会较好地向D逼近。那么每次迭代测试提取的非均匀性信息则为：

nuc＝D＝DÄ(7)

第2次测试提取的非均匀性信息则为：

nuc2＝D1(9)

校正后的残余非均匀性为：

D2＝D1－nuc2＝D－D－D1＝D1－D1(10)

新一轮测试提取的非均匀性信息为：

D2＝D2(11)

依次类推，当进行到第次测试时，有：

Dp＝D－(D＋D1＋…＋Du－1)＝Dp－1－Du－1(12)

Du＝Dp(13)

那么有：

nuc＋1＝Du＝×(Dp－1－Du－1)＝Du－1－

Du－1＝(－)Du－1＝Du－1＝RGD(14)

根据式(14)，式(12)中间部分数据可改写为：

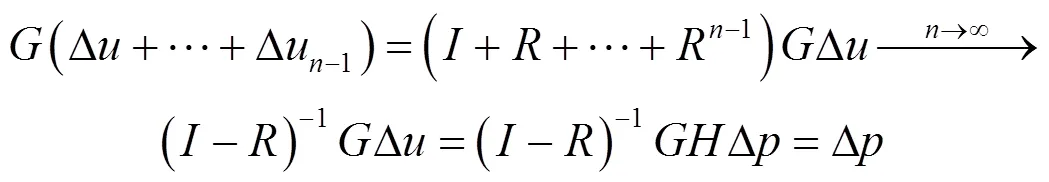
由式(12)和式(15)可知，当®¥时，Dp®0。由图4可知，式(15)中最左边的表达式即为系统中非均匀性信息寄存器中的累加值，即：

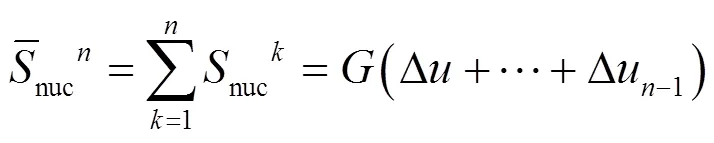
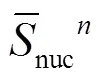
3 测试方法的数值仿真分析

3.1 PSF估计误差的影响

在Matlab下以16×16图像尺寸为例对迭代过程进行数值仿真。设置电阻阵列的非均匀性为10%，实际退化PSF平滑因子＝0.5时，5种不同PSF估计下非均匀性测试信息提取后校正图像的残余非均匀性数值仿真结果如图5所示。

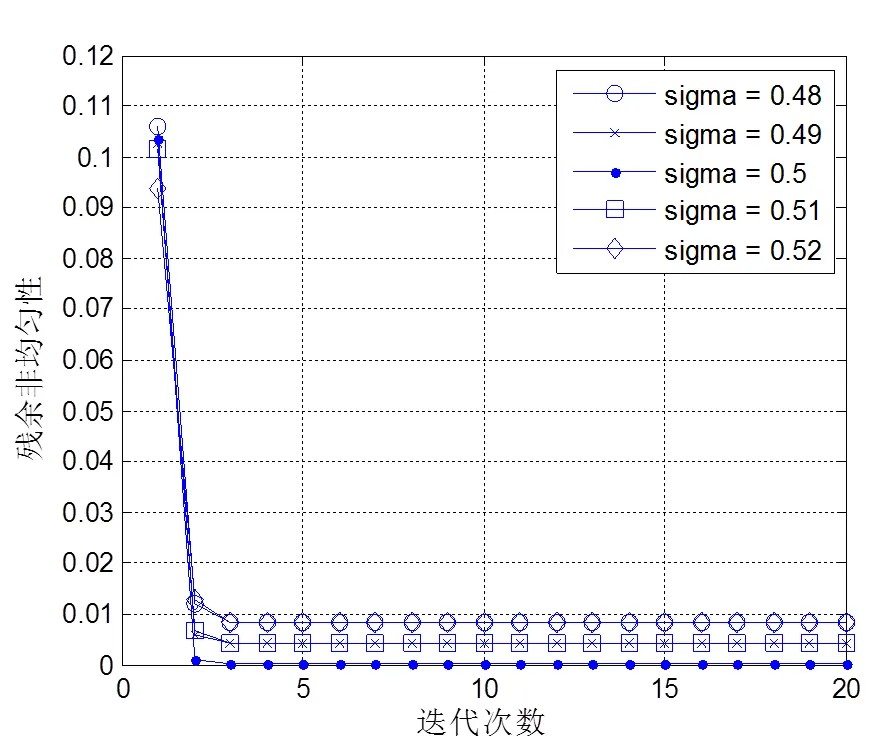
图5 基于PSF估计的迭代测试数值仿真结果

仿真结果表明：当PSF函数估计误差不超过5%，迭代的残余非均匀性指标Dp随着测试次数的增加快速收敛到一个相对稳定的水平。校正最终的效果取决于PSF估计的精度，当理想状态下估计出真实的PSF时，迭代3次残余非均匀性已优于0.1%。迭代20次后电阻阵列投射出的校正图像如图6所示。

当PSF估计存在误差时，校正后的图像仍然存在一定的边缘效应。但与图3相比，由于迭代可获得更多的信息，边缘效应得到了明显的改善。当PSF估计达到理想值时，边缘效应消失。值得关注的是，当PSF估计误差存在时，残余非均匀性存在主要的原因是由于边缘效应的存在。

3.2 不同PSF下迭代测试效果

为验证不同图像退化情况下迭代测试的效果，假设存在5%的PSF估计误差，对6种不同的实际退化情况进行数值仿真，结果如图6所示。

仿真结果表明：在不同的图像退化情况下，迭代测试均达到了较快的收敛速度。当测试次数达到5次以上时，残余非均匀性指标已收敛到一个稳定的值。随着PSF平滑因子的增加，最终的残余非均匀性指标随之变差。根据上面的分析，残余非均匀性存在主要受边缘效应的影响，若仅考虑电阻阵列常用的中心区域（如图7所示），所有PSF情况下最终的残余非均匀性都到达了非常好的水平。

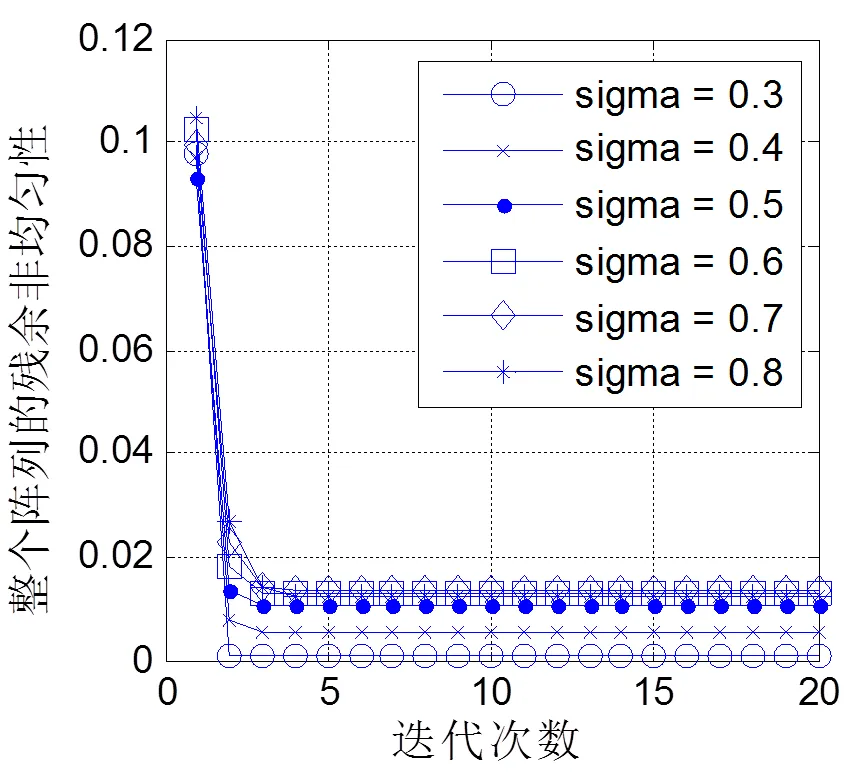
图6 整个阵列的残余非均匀性

图7 阵列中心的残余非均匀性

4 结论

与文献[8]提出的多次迭代盲复原测试相比，基于PSF粗估计的迭代测试具有更快的收敛速度和更好的校正效果。能够适应更宽的平滑因子参数范围，而且迭代测试中大量采用加减法计算，提高了数据处理速度，具有更高的实用性。

本文提出了全屏驱动的非均匀性测试方法，着重于利用图像数据处理的手段解决由光学系统引起的相邻辐射像元输出串扰的问题，数值仿真验证了其算法的有效性。在实际工程应用中，测试数据往往受到环境辐射的影响，较低的信噪比引入了新的测试误差。全屏驱动则可通过大面积辐射能量输出最大降低杂散辐射的影响，获得较高的信噪比，因此具备较高的工程有效性。但当测试电压较高时，驱动所有的辐射像元导致系统供电电流变得很大，将会出现明显的总线压降现象。并且此时，大量的散热给衬底冷却系统带来了压力，导致散热不均，引入额外的非均匀性。所以，全屏测试的应用应放在低电压区点位测试。

另外本文研究的前提仍然是1:1的映射比例和精确的像元对准，非一致映射比例下情况下可能产生的影响，以及像元的对准方法是值得继续深入研究的问题。

[1] 肖云鹏, 马斌, 梁平治. 电阻阵列动态红外景象投射器单元电路研究[J]. 科学技术与工程, 2006, 6(14): 2116-2118.

[2] 李守荣. 微桥电阻的辐射特性研究[J]. 红外与激光工程. 2005, 34(4): 442-445.

[3] 马斌, 程正喜, 翟厚明, 等. 国产电阻阵列的发展趋势[J]. 红外与激光工程. 2011, 40(12): 2314-2322.

[4] 马斌, 张凯, 高蒙, 等. 256×256高帧频及128×128高占空比电阻阵列的性能测试结果[C]//北京:第十届全国光电技术学术交流会, 2012: 109-115

[5] 娄树理, 周晓东, 董言治. 动态红外景象生成方法研究[J]. 红外与激光工程, 2004, 33(4): 427-431.

[6] Jr James A Buford, David Cosby, Dennis H Bunfield et al. AMRDEC HWIL PC Scene Generation[C]//,,:. 2007, 6554: 0E1-0E5.

[7] Chad L Christie, Efthimios Gouthas, Owen M Williams. Graphics processing unit(GPU) real-time infrared scene generation[C]//,,:. 2007, 6554: 0C1-12.

[8] 苏德伦, 张金生, 廖守亿. 电阻阵列非均匀性测试[J]. 红外技术. 2010, 32(6): 345-352

[9] 杨春伟, 廖守亿, 苏德伦, 等. 电阻阵列非均匀性测试与校正[J]. 红外技术, 2013, 35(6): 345-349.

[10] 顾亚芳. 高斯模糊图像的盲复原[D]. 南京: 东南大学, 2005.

[11] 王艳. 盲目图像复原方法研究[D]. 重庆: 重庆大学, 2006.

[12] 王辉. 基于神经网络的退化图像复原算法研究[D]. 上海, 上海交通大学, 2006.

Resistor Array Non-uniformity Test Based on PSF Estimation

SU De-lun1,2，LIAO Shou-yi1，ZHANG Jin-sheng1

(1.，710025，；2.96111，715400，)

The non-uniformity of resistor array dynamic infrared scene projector is a kind of fixed pattern spatial noise which makes a great impact on the quality of the output infrared image. The accuracy of the test data is vitally important for the non-uniformity correction. The spread of the radiant energy is a main source of error in flood test. The limitation of classical image restoration method was analyzed. A new iterative test method based on PSF rough estimation was presented. The impact of estimation error on convergence speed and test accuracy was analyzed and the method effect under different PSF condition was evaluated. Numerical simulation indicates that the new method has features of reducing calculation complexity, fast convergence speed and adaptability of more widely range of smooth factors. The new method can effectively restore the degraded image to extract the true non-uniformity image and attain good correction result.

resistor array，non-uniformity test，PSF estimation，degraded image restoration

TN215

A

1001-8891(2015)06-0479-05

2014-02-26；

2014-09-15.

苏德伦（1981-），男，辽宁凤城，锡伯族，在站博士后，主要从事红外成像半实物仿真与实时控制系统方面的研究。

某院重点平台建设项目；中国博士后科学基金，编号：2012M512。