运输方式选择多目标优化问题研究
2015-04-02谢长军
谢长军
摘 要:运输方式的选择问题直接关系到货物的运输费用、运输时间以及运输质量。只有通过对运输方式进行选择优化从而到达最佳优化效果才能够从根本上解决货物的运输问题。特别是在当今社会高速发展时期,物流建立的较为发达,同时国内的经济飞速发展。在新的形势下,如何使运输方式的选择达到最优化成为企业生存的一个重要问题。为此,首先分析了当前不同交通工具的基本经济和技术特征,进而提出了适用于多城市的最优化交通组合方式模型,即运输进化规划模型。最后,提出了如何求解最优路径的科学解决办法。
关键词:运输方式;选择;多目标;优化
1 概述
交通运输是一个国家经济发展的命脉,同时也是提高人们生产和生活水平的重要保障。特别是在我们国家这种发展中国家的条件下,交通运输虽然快速发展,但是仍然不能够满足当前国家经济发展和社会发展的需要。为此,就必须能够通过当前现有的外部条件,通过科学的手段进行运输方式中选择多目标的优化。只有这样才能够使运输方式被社会更好的运用,从而为社会创造更多的财富。当然,运输系统是一项较为复杂的系统,其牵涉到多学科的理论课题,必须以多学科为背景深入探讨来确定研究视角和研究方式。文章在考虑现有交通运输通道的背景之下,分析了当前不同交通工具的基本经济和技术特征,进一步提出适用于多城市最优化佳通方式组合模型,最后,在此基础上提出了科学规划方式和思路。
2 多目标运输通道的分析及存在的主要问题
2.1 多目标运输通道分析
经济的全球化使得一些大型物流企业不仅从事近距离的货物运输,还从事一部分远距离运输。由于各种交通运输通道都具有自身的特点和优势,因而对于物流企业而言就需要对运输通道加以分析,选择最优化的目标组合方式,从而能够以极低的成本,按质按时的完成企业的运输任务。通道是由交通线路组成的,对这些交通线路的分析其实可以等同于对网络的分析。网络分析则包含了最短路径分析和最优化路径分析等。因而,在这里,可以通过网络分析的方式为手段进行多目标的运输通道分析。
多目标运输通道的优化是指包含两个或者多个目标的优化问题。例如,假设有一批货物从起始点O运输到目的地P,其沿途经过m座城市。此m座城市中任意相邻的两座城市之间可以有n种不同的运输方式供选择。因而,多目标运输通道的分析归根结底是选择某种运输方式组合,使运输总费用尽量降低,运输总时间尽量缩短。
多目标的优化问题需要从多因素出发,通过分析目标的性能,使最终几项指标达到最优化。将多目标运输通道的优化假设成n个决策变量存在n维的决策空间中,m个目标函数则存在于m维的目标空间中,其数学模型可以简单概括如下:
寻求最小值y,即miny=F(x)=(f1(x),f2(x),…,fm(x)),從而满足公式:
,其中,该公式中的x为决策变量,
y为目标函数。
2.2 存在的主要问题
首先,具有较高级别的运输系统呈现带状区域,其中包含了若干相互平行的线路。而地图中一般缺乏对相应的运输通道的整体空间描述以及对表示方法的研究。因而,在进行数据分析时缺乏一定的资料,影响方式线路的优化选择。其次,运输通道包含多种目标的运输方式交通连接点。正式由于这些交通连接点的存在,使得多种运输费方式成为了使整个枢纽区域变化复杂的系统,严重的影响着运输方式多样化的选择。再次,对于交通运输方式的综合评价方法颇多,常见的有综合评判法、模糊评判法以及灰色评价法等,这些方法当前遇到的难题是如何使用合适的方法反应评估对象的整体水平及标准。最后,现有的最佳目标路径寻找方法有三十余种。虽然一些传统方法尽管容易实现并且具有运算快速的特点,但是一些传统方法只能针对袁术方式选择中的凸方法,而对于非凸方法则不行。同时,决策者在决策过程中需要不断地根据模型提出自己的偏好结构信息,却不能够准确的描述自己的偏好结构。产生方式方法有待提高,付出的代价较大,时间效率较低。
3 运输方式多目标优化模型建立及求解
3.1 模型建立
假设运输模型满足以下两个条件。第一,运输量在某一个城市之间不能够分割,也就是说在某个城市只能选择一种云技术方式。第二,企业的运输成本和运输的距离呈现线性相关。由此,依据相关的分析方法,可以将本问题建立运输方式多目标优化模型:
满足以下六个约束条件,即:
根据公式,该目标函数在整个运输过程中所能达到的最低成本为目标,其费用分别来自于中转费、运费以及惩罚费用三者。
其中,第一个约束条件的假设为假定城市之间只能选择一种交通方式,也就是之前提到的运输量不再分割条件。第二个约束条件为在城市中只能进行一次运输装换。第三个约束条件确保整个运输的连续性。第四个约束条件是货物必须在规定的期限内到达目的地。第五个约束条件是货物的运输量不能够超过该运输工具的运输能力,第六个约束条件则是决策变量只能在{0,1}中选取。
3.2 求解
根据以上建立的运输方式选择多目标最优化模型,将原问题转化为一个带有时间约束条件以及能力约束条件的最短路径运输问题。通过模型问题的转化,该问题能够使用Dijkstra算法进行对两种约束条件的最优化求解。其中,解决该问题的是时间复杂度为O(m2)。
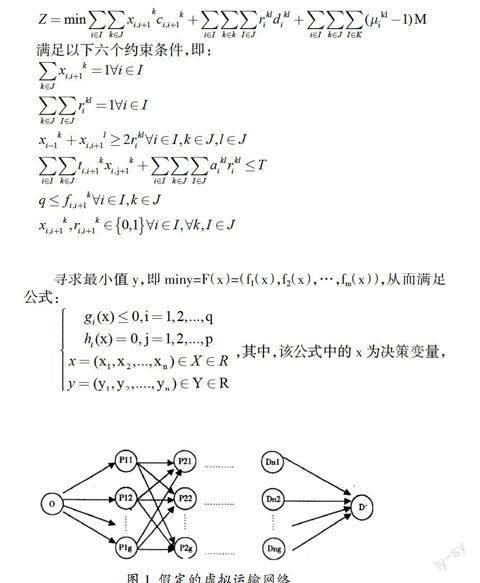
首先,构造运输网络,假设始发点为O,将其他城市的分别扩展为g个城市,并且假定终止点为D',那么可以构建出如图1所示的网络。
图1 假定的虚拟运输网络
其次,在不考虑时间约束条件的情况下,求出从起始点O到终止点D'的最短路径。进一步在此基础上使用Dijkstra算法进行对两种约束条件的最优化求解。下面通过具体事例加以说明。假设有五个城市,其中两两城市之间可供选择的运输方式有三种,即铁路、公路和航空。假定运输量为20个单位,最迟三十天运输完毕。其中城市之间的运输费用和运输时间如图2所示,城市之间的运输工具运输能力如图3所示,不同运输方式之间的换装费用及时间如图4所示。那么,根据上述解决思路,可以构建出如图5所示的运输网络示意图。
图2 城市之间的单位运输费用及运输时间
图3 城市之间三种运输方式的成本
图4 城市之间不同运输方式转化的费用及时间
在不考虑时间约束条件下,可以得到从0到13的最短路径为0,2,6,7,12,13。其中,从城市1到城市2选择铁路,城市2到城市3选择航空,城市3到城市4选择铁路,而城市4到城市5则选择航空。由此计算得出整个花费为204,总时间消耗是32天。进一步,利用上述思路解决,使其满足时间约束条件,将城市3和城市4之间的铁路换成航空,算得总费用261,总时间19天。
4 结束语
综上所述,通过运输方式选择多目标模型建立和模型简化,使用Dijkstra算法能够便捷的求出城市之间多种交通方式的最优化组合,这对于解决现代物流业存在的最优路径问题无疑具有重要的作用。当然,文章中的方法在拓展到网状结构的城市群还有待进一步的验证和探讨。
参考文献
[1]王涛,王刚.一种多式联运网络运输方式的组合优化模式[J].中国工程科学,2005(10).
[2]张得志,凌春雨.多种运输方式的组合优化模型及求解算法[J].长沙铁道学院学报,2002(4).
[3]张建勇,郭耀煌.一种多式联运网络的最优分配模式研究[J].铁道学报,2002(4).