测量坐标转换系统设计与实现

牛丽娟 王腾军 李立功

(1.陕西铁路工程职业技术学院,陕西 渭南 714000； 2.长安大学地质工程与测绘学院,陕西 西安 710054)

测量坐标转换系统设计与实现

牛丽娟11王腾军22李立功11

(1.陕西铁路工程职业技术学院,陕西 渭南 714000； 2.长安大学地质工程与测绘学院,陕西 西安 710054)

本文介绍了坐标转换的方法及流程,详述了利用C#语言构建测量坐标转换系统的设计过程,并以CGCS2000大地坐标到西安80平面坐标的转换为例,介绍了其具体实现过程。通过对转换结果进行精度分析,能够满足一定的要求。

坐标转换;布尔莎模型;四参数转换模型;坐标转换系统

2008年7月1日,2000国家大地坐标系(简称CGCS2000)在全国范围内正式启用［1］。但我国目前的测绘成果以北京54坐标和西安80坐标居多,所以就需要通过坐标转换,将原有的测量成果以较高的精度转入CGCS2000坐标系下使用［2］。

测量坐标转换主要包括坐标系转换和坐标基准转换两方面的内容。坐标系转换是指在同一基准下的空间点不同坐标形式之间的转换。在椭球体参数已知的情况下,可以直接利用确定的公式来实现,如高斯正反算、同一点的大地坐标与空间直角坐标之间的相互转换等。坐标基准转换是指不同基准下测量坐标之间的转换。由于椭球参数不同,且没有确定的数学关系,往往需要先求取转换参数再进行转换,其实现的关键在于确定转换的数学模型和转换参数［3一4］。

通过对不同坐标基准转换模型的理论分析,本文采用基于七参数的空间转换模型——布尔莎模型和四参数平面转换模型［5］。根据各种坐标转换算法,笔者利用C#语言构建了测量坐标转换系统,实现了高斯平面直角坐标、大地坐标与空间直角坐标之间的相互转换,以及坐标换带计算等功能。本文以CGCS2000大地坐标向西安80平面坐标的转换为例,详细阐述其转换与实现过程。

1 坐标转换

1.1 转换方法

当测区内公共点较少时,可以选择整体转换法,即整个转换区域求解一套转换参数,进而进行坐标转换。鉴于在不同区域地面网的系统误差并非完全相同,当公共点较多时,可以将整个转换区域分成若干个分区,然后对各分区分别计算转换参数并进行坐标转换。考虑到各分区在接边处转换参数的连续性,可以在各分区之间的重叠部分选择一些重合点,并反复使用求解转换参数。分区转换法可以提高坐标转换的精度。

1.2 转换流程

1.2.1 公共点选取

公共点一方面可以通过实测获得,另一方面可以通过收集获得。在进行转换参数计算时,鉴于粗差点会明显降低转换参数的精度,必须先进行粗差点的剔除工作［6］。为了提高测量坐标转换精度,应对参与求取转换参数的公共点进行分析、筛选、试算,尽量选取高等级、高精度的公共点,且使所选择的点均匀分布在整个控制网中［7］。

1.2.2 转换参数计算模型

(1)布尔莎模型

布尔莎模型是空间七参数坐标转换常用的数学模型,且表示如下：

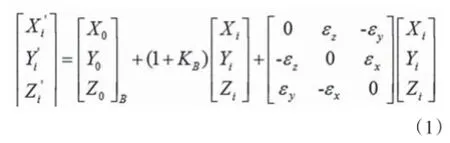
上式中,(X′i,Y′i,Z′i)为目的坐标系下的空间直角坐标；(Xi,Yi,Zi)表示原坐标系下的空间直角坐标；(XOB,YOB, ZOB)为三个方向上的平移参数；εx、εy、εz为旋转参数,KB为缩放参数。

设有n(n≥3)个公共点,在求解转换参数时,公式(1)可等价变换为：

有n个公共点,则可以列出3n个误差方程,其误差方程矩阵形式为

其中,V表示残差矩阵,A为系数矩阵,X为未知七参数,L为闭合差：

若各观测量为等精度(设权阵为单位权),则可得转换参数的最小二乘解：

(2)四参数平面转换模型

在一个小区域范围内,同一点在两种坐标系中的高斯平面坐标,可以认为是由两个坐标系进行旋转和尺度伸缩而产生的,可以用四参数平面转换公式来表示,具体表达如下：

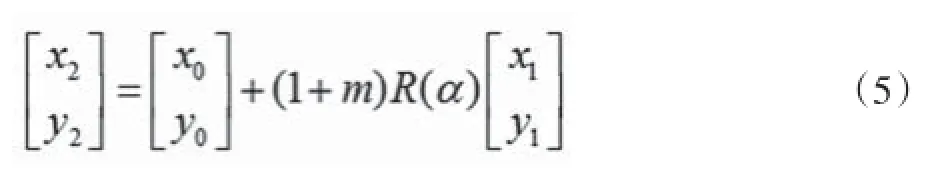
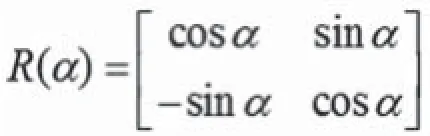
由于α角很小时,近似地有cosα=1,sinα=α,忽略其间的互乘项,则公式(5)可变换为：

选取n(n≥2)个公共点,则可以列出2n个误差方程,其矩阵形式为：

其中,

若各观测量为等精度(设权阵为单位权),则可得转换参数的最小二乘解：

1.2.3 坐标转换实施步骤

以CGCS2000大地坐标向西安80平面坐标的转换为例,具体坐标转换实施步骤如下：

(1)收集、整理坐标转换区域内公共点成果。

(2)分析、选取用于计算坐标转换参数的公共点。

(3)确定坐标转换参数计算模型。

(4)对两坐标系下公共点的坐标形式进行转换。

①若采用布尔莎模型,具体步骤为：

a.取当地中央子午线,将公共点的西安80坐标系下的平面坐标根据1975国际椭球参数进行高斯反算,求其大地坐标,进而求得空间直角坐标；

b.根据2000参考椭球参数,将CGCS2000大地坐标换算成空间直角坐标；

c.根据公共点在CGCS2000和西安80坐标系下的两套空间直角坐标,求出布尔莎模型七个转换参数的最小二乘解。

②若采用四参数平面转换模型,具体步骤为：

a.取当地中央子午线,将公共点的CGCS2000根据2000参考椭球参数进行高斯正算,求其高斯坐标；

b.根据公共点在两个坐标系下的两套高斯平面坐标,求出平面转换模型四个转换参数的最小二乘解。

5.分析参与坐标转换的各公共点残差,剔除粗差点后重新计算转换参数,直到满足精度要求。

6.当坐标转换残差满足精度要求时,计算最终的坐标转换参数,并估计其精度。

7.将转换点的原坐标系下坐标换算为空间直角坐标或高斯坐标,然后根据转换参数,计算目的坐标系下的坐标,进而转化为其他所需的坐标形式。

2 坐标转换系统设计与实现

鉴于上述坐标转换的模型和步骤,笔者利用C#语言设计了测量坐标转换系统,目的在于弥补目前市面上坐标转换软件功能的不足,满足测量工作者的不同需求。

2.1 总体设计

在系统总体设计时,主要考虑坐标转换内容、转换模型、转换方式及用户界面等几方面的内容。输入转换数据时,若数据量较少,可以直接输入；若转换点较多,需要采用文件化管理(格式为文本文件),相应地也就需要有文件的导入、导出功能。用户界面应是与用户交互、友好的,能够方便用户添加、编辑、修改坐标数据,并可以对计算的转换参数进行保存、导入、导出。

2.2 功能设计

该系统充分利用C#面向对象的程序开发功能［8］,采用模块化设计,以人性化操作为目标,利用文件接口方式,实现模块间的有机结合。界面主菜单主要有参数设置、参数计算、坐标系转换、平面坐标转换、坐标基准转换、换带计算、角度转换等7部分组成,每个子菜单都以弹出对话框形式与用户交互,在对话框中,添加可编辑的数据表格控件DataGridView,体现直观性、人性化。

2.3 流程设计

根据坐标转换的基本原理和方法,以及系统的内容和功能设计,对坐标转换的处理流程进行设计,其流程图如图1所示。

图1 坐标转换系统流程图

2.4 系统实现

根据2.2.3中介绍的坐标转换步骤,笔者先将西安80平面坐标通过高斯反算转换为大地坐标形式,然后转换为空间直角坐标,具体实现如图2和3。

图2 高斯反算

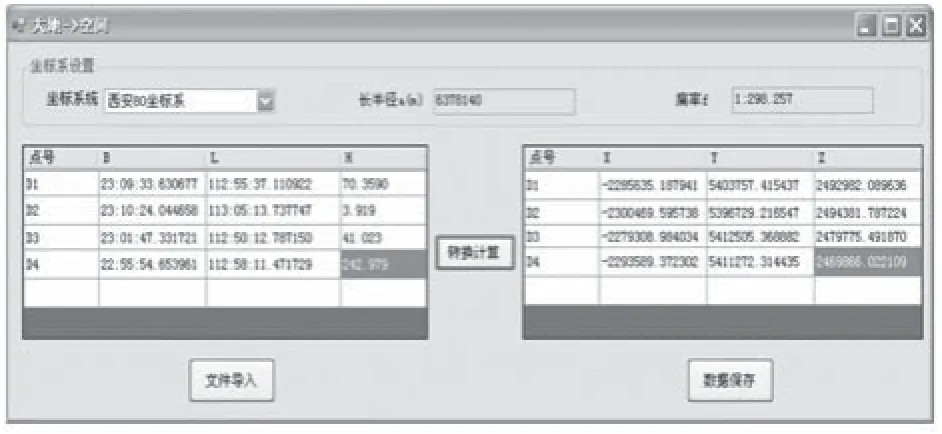
图3 西安80大地坐标转换为空间直角坐标

同理,将CGCS2000大地坐标转换为空间直角坐标形式。

点击“参数计算”下的“七参数计算”(如图4),选择原坐标系和新坐标系的类型,相应的参考椭球参数将随之改变。将公共点的两套空间直角坐标通过“文件导入”形式导入到DataGridView中。

图4 七参数计算

确定公共点坐标无误后就可以直接“解算七参数”,查看弹出对话框中显示的转换参数,并“保存参数”以备导入参数时使用。

解算出七参数后,在“坐标基准转换”下选择“大地→平面”子菜单,选择原坐标系和新坐标系类型,“文件导入”待转点的坐标,并导入求取的七参数,点击“转换计算”,就可以在右边的DataGridView中查看转换结果了,并可通过“数据另存”保存到文本文件中,转换结果如图5。

图5 CGCS2000大地坐标转换为西安80平面坐标

3 结语

坐标转换是测量工作者经常遇到的问题,本文通过自编程序,设计并实现了测量坐标转换系统,并以CGCS2000大地坐标到西安80平面坐标的转换为例,详述了坐标转换的方法、流程及具体实现过程。在精度方面,空间转换模型的残差中误差分别为：Mx= 0.138mm,My=0.396mm,点位中误差Mp=0.419mm,可以认为所求的转换参数是可靠的。在以后的工作中,期望对其他的坐标转换方法和数学模型进行更多的验证,并进一步完善、优化改系统功能,以满足更多用户需求。

［1］魏子卿.2000中国大地坐标系及其与WGS一84的比较［J］.大地测量与地球动力学,2008,28(5):1一5.

［2］魏子卿.我国大地坐标系的换代问题［J］.武汉大学学报,2003,28(2):138一143.

［3］武继军.不同大地坐标系间坐标转换模型研究［J］.河南理工大学学报,2006,25(5):383一385.

［4］牛丽娟.测量坐标转换模型研究与转换系统实现［D］.长安大学,2010.

［5］朱华统.大地坐标系的建立［M］.北京:测绘出版社, 1986.

［6］柳光魁,赵永强,王振禄,等.西安1980坐标系与WGS一84坐标系转换方法及精度分析［J］.测绘与空间地理信息, 2006,29(6):40一41.

［7］徐仕琪,张晓帆,周可法,等.关于利用七参数法进行WGS一84和北京54坐标转换问题的探讨［J］.测绘与空间地理信息,2007,30(5):33一38.

［8］黄国平.C#实用开发参考大全［M］.北京:电子工业出版社,2008.

Designand ImPlementation of Geodetic Coordinate Transformation System

Niu Lijuan1Wang Tengjun2Li Ligong1
(1.Shaanxi Railway Institute,Weinan Shanxi 714000；2.School of Geology Engineering and Geomatics,Chang’an University,Xian Shanxi 710054)

This paper introduces the methods and processes of coordinate transformation,explains the design processes of geodetic coordinate transformation system with C#language in detail,then introduces the specific implementationprocesses by the example of geodetic coordinates in CGCS2000 to Gauss plane coordinates in Xian 80 coordinate system.By analyzing the precision of transformation results,it can meet certain requirements.

coordinate transformation;Bursa一wolf model;four一parameters transformation model;coordinate transfor mation system

P226.3

A

1003一5168(2015)07一0125一4

2015一6一4

陕西铁路工程职业技术学院科研立项研究生项目(2012一9)。

牛丽娟(1984一),女,助教,研究方向:测绘教学及科研管理。