一种无线传感器网络故障节点检测算法*
2015-04-01徐磊磊徐保国
徐磊磊,徐保国
(轻工过程先进控制教育部重点实验室 江南大学,江苏 无锡214122)
0 引 言
无线传感器网络(wireless sensor networks,WSNs)中的节点可能会遇到两种类型的故障,从而降低网络性能[1,2]。一种是功能故障,这将导致个别节点崩溃、包损失、路由故障[3];另一种是数据故障,除了它的检测结果错误,其它可以正常工作[4]。故障节点的存在对系统有很大影响,因此,检测这些故障节点并将其剔除是非常重要的[5]。
本文提出一种检测故障节点的方法,该方法提供了一个包含所有的故障节点的黑名单,无需事件或模型假设,根据特定事件节点的读数排列顺序,通过识别节点序列中违反排名的节点,将故障节点加入黑名单。算法对实际应用中的噪声环境和子序列估计问题分别提出了相应的解决方法。仿真实验表明:在不同的网络设置下,漏检率和误检率均较低,算法具有良好的性能。
1 故障节点检测设计
1.1 区域划分
如图1 所示,区域内所有节点间的垂直平分线将区域划分为若干个子区域[6],每个子区域可以通过子区域和所有的节点距离关系的唯一的距离序列来标识。由于故障节点和噪声影响,有故障读数的检测序列会违反距离序列的几何约束,可能是所有N!个节点序列中的任意一个。因此,给定事件的检测序列后,需估计事件发生的子区域。这实质上是将检测序列与距离序列进行有效映射。

图1 区域划分举例Fig 1 Examples of region division
1.2 检测序列映射
令N 个节点将平面分成M 个子区域,用距离序列集V={s1,s2,…,sM}表示。设是单个事件的检测序列,s 为事件发生的子区域的距离序列。s 为样本空间V 的随机变量,用{A1,A2,…,AM}表示M 个子区域的大小,则s 的先验分布为

通过最大后验(MAP)估计法来估计

接下来要找出一个距离序列si∈V 使式(2)最大化。对于任意si∈V,Pr(si)式(1)已经给出,唯一未解决的问题是如何计算
设α 为传感器节点的次品率。¯s[k]和si[k]分别表示N 个节点序列和si中第k 个节点。当所有的1≤k≤N,均成立,有两种可能:一种是所有节点均正常,另一种是有w 个故障节点,但在这种特殊的情况下,这些节点没有改变序列,可能性为


第二种:¯s 中第k 个节点是正常节点,在这种情况下从k+1到l 必有故障节点,图2 中若节点6 正常,节点3,4,5中必有故障节点,从原始序列中去除这些节点获得新的序列s″i和,均为1-2-6-7-8-9,这种情况下,原来的条件概率)取决于新的条件概率正常下的条件概率为
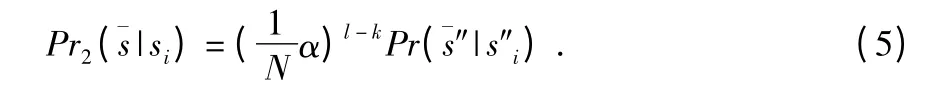
最终条件概率的公式为
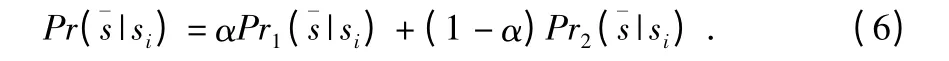
式(6)是递归的,递归过程一直进行到两个序列完全相同。通过式(6)计算任意si∈V 下的条件概率,再由式(2)可以MAP 估计。

图2 条件概率计算Fig 2 Conditional probability computation
1.3 排序差检测
1.3.1 平均排序差
设¯si对应的样本估计为n 为样本大小,定义样本i中节点k 排序差di(k)为

式中 R(*,k)为节点k 在序列*中的排序,则在n 个样本中节点k 的平均排序差D(k)为

定理:如果节点q 故障,那么,它的平均排序差D(q)要比界B 大

式中 N 为网络中节点总数,Ne为故障节点的个数,μe为故障节点平均排序差的算术平均值。
证明:设1~Ne为故障节点,剩余为正常节点。当只有一个故障节点时,观察到对于单一的故障节点k,其排序差为d(k),至多让d(k)个节点的排序相差1。如图3(a)所示,故障节点4 向左移动两位使得2 个节点(2 和3)的顺序改变了1,与排序差d(4)=2 相等。
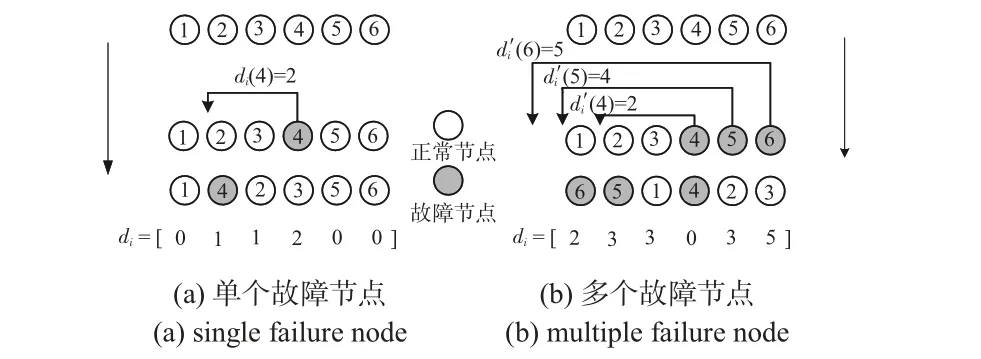
图3 故障节点对排序差的影响Fig 3 Effect of fault nodes on ranking differences
当其余Ne-1 个故障节点出现时,一个故障节点最终排序会被其余故障节点影响。图3(b)中节点2 和3 的排序差为3,这是由于3 个故障节点导致的,虽然最终的d(4)=0,但其影响仍然存在。因此,被节点4 影响的节点数为开始的d'(4)=2。给定任意的节点k 的最终排序差d(k),原始移动d'(k)最大可能值为d(k)+Ne-1,即最多影响d(k)+Ne-1 个节点。
正常节点不会改变其他节点的排名顺序,给定的d(k),一个正常节点p 被节点k 影响的预期排序差为dk(p)

等式两边取期望

一个正常节点p 被所有故障节点影响的预期排序差的上限为

其中,μe为受所有故障节点的影响的平均排序差的平均值
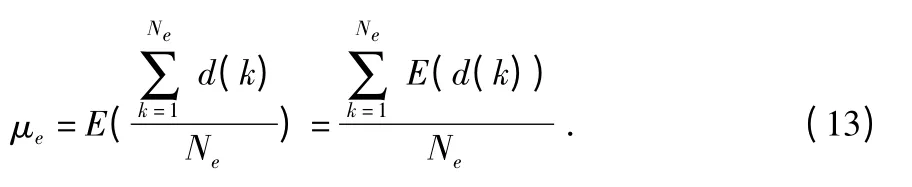
式(12)不等号成立的条件为Ne个故障节点对节点p的影响均向同一个方向。当样本足够大时,用期望替代样本平均值,式(12)变为

令B 等于上述不等式右边的部分,则任意正常节点的平均排序差的上限为B,如果一个节点的平均排序差大于B,那么,它必然为故障节点。
1.3.2 检测算法
由于故障节点Ne预先不知道,需要估计Ne的大小,其基本思想是找到所有平均排名差高于B 的节点,给定有序节点序列n1-n2…-nN,找到分割点k,使得{n1,n2,…,-nk}为故障节点估计。检测算法伪代码如下


首先,初始化,从平均排名差最大的节点n1开始,依次检验排序差,将大于B 的节点加入到黑名单中。更新Ne,μe,B。当循环在节点nk+1时被打破,得到黑名单{n1,n2,…,nk}。
2 算法应用问题解决方法
2.1 噪声环境
在强噪声环境,普通节点有时会表现为故障节点,为了解决该问题,使用统计方法在序列{n1,n2,…,nk}中筛选出可能的正常节点。给定故障节点估计{n1,n2,…,nk},其余的点{nk+1,…,nN}被认为是正常节点,那么,正常节点的样本平均值μ 和排序差的样本方差σ2可计算出。将节点排序差不大于^μ+3^σ 从黑名单序列中移除。
2.2 子序列估计
实际中单个事件检测序列¯s 的长度要比N 小很多。设L 为检测序列长度的上界。给定¯s,其相应的si也被截断,选择si的截断长度为2L。对于子序列来说,存在两个问题,首先,开始时两个序列的长度不相等,因此,多数情况下¯s 和si不相同。其次,由于si也被截断,不能确保存在si[l]使得¯s[k]=si[l]。因此,在递归计算Pr(¯s|si)做出如下改进:1)递归终止条件放宽到si从后面开始移除若干个节点后被¯s 截断。2)对于每对不匹配的节点¯s[k]≠si[k],如果¯s(k)在si中不存在,若正常则说明至少有L 个故障节点,这种情况可忽略,因此,直接被认为是故障节点。
3 仿真与结果分析
仿真实验中将100 个传感器节点随机部署在250 m×250 m 区域内,通信半径25 m 和事件数目为50,节点和事件随机生成。L 设为10,采用最常用的对数衰减模型。随机噪声服从分布,σX缺省值是4。所有仿真结果取20 次平均值。设α 准确,则排序差前αN 个节点被视为故障节点,这是一种理想情况,记为α 检测。当α 不准确,用检测算法得到故障节点数,记为B 检测。
两个指标用于评估算法性能:漏检率和误检率。前者定义为故障节点检测为正常的比率,后者为正常节点检测为故障的比率。
3.1 α 检测与B 检测性能比较
图4 反映了α 检测和B 检测分别在有噪声和无噪声环境下的漏检率。可以看出:1)两种检测漏检率均在10%以下,当节点缺陷率α 低于10%时漏检率低于4%。因此,两种检测均可以有效检测出故障节点。2)α 检测总是比B检测漏检率低,这是因为α 检测可以直接根据平均排序差选择前αN 个节点作为故障节点,而B 检测要采用检测算法找出故障节点数目。因而α 检测具有更好的性能。3)由于噪声的存在,α 检测与B 检测漏检率略微增加,但仍可以检测出超过90%的故障节点。图5 对应于上述4 个场景中的误检率,可以看到大部分的误检率是1%左右,意味着正常的节点只有极少部分被误判,因此,该算法性能良好。

图4 两种检测漏检率比较Fig 4 Comparison of two kinds of miss detection rate

图5 两种检测误检率比较Fig 5 Comparison of two kinds of false detection rate
3.2 不同网络密度的影响
将网络区域边长从150 m 增加到350 m,节点数目保持不变。图6、图7 曲线反映了B 检测在不同网络密度下的性能:1)区域边长从300 m 增加到350 m,漏检率增加5%左右;区域边长从250 m 增加到300 m,误检率也增加了。这是因为较低的密度,事件通信半径内的节点的数量变小,节点序列变短,信息较少,估算序列较不准确。2)区域边长从200 m 下降到150 m,误检率没有下降。这是因为当密度越高,更多的节点在检测范围内,距离事件具有相似距离。加上噪声的存在更多的节点具有类似的读数。因此,误检率最低的是中等密度的网络,误检率多为2%左右。
4 结 论
本文提出一种无线传感器网络故障节点的检测方法,提供了一个包含所有的故障节点的黑名单,无需事件或模型假设,通过识别节点序列中违反排名的节点,找到故障节点。从理论上证明检测序列和估计序列的平均排序差可作为故障节点的判断指标,并对算法在实际应用中噪声环境和子序列估计问题分别提出了相应的解决方法。仿真实验表明:在不同的网络设置下,漏检率和误检率均较低,因而,算法具有良好的性能。

图6 网络密度对B 检验漏检率的影响Fig 6 Effect of network density on B-detection miss rate
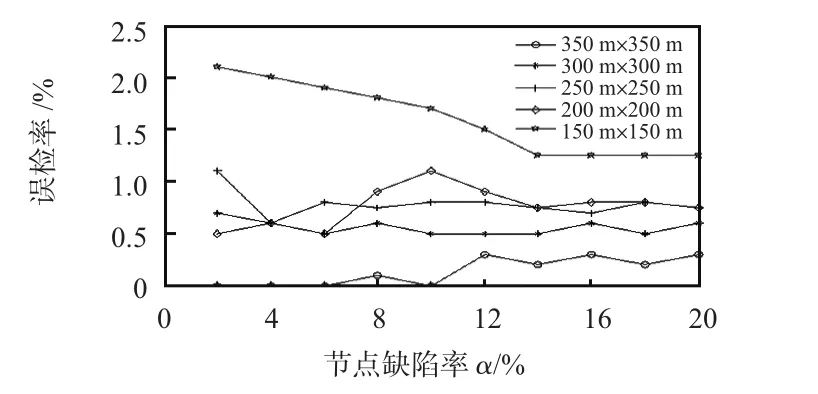
图7 网络密度对B 检验误检率的影响Fig 7 Effect of network density on B-detection false rate
[1] Ju Hailing,Miao Yong,Li Tianpu,et al.Overview of wireless sensor networks[J].Computer Research and Development,2005,42(1):163-174.
[2] 孙利民,李建中,陈 渝,等.无线传感器网络[M].北京:清华大学出版社,2005.
[3] Cullar D,Estrin D,Strvastava M.Overview of sensor network[J].Computer,2004,37(8):41-49.
[4] 赵亚凤,任洪娥.基于无线传感器网络的同时定位与跟踪[J].传感器与微系统,2014,33(5):55-58.
[5] Jia Z X,Wu C D,.Zhang Y Z,et al.Distributed grid location estimation scheme based on euclidean distance[C]∥IEEE 3rd Conference on Industrial Electronics and Applications,2008:1128-1132.
[6] Joo G L,Rao S V.A grid-based location estimation scheme using hop counts for multi-hop wireless sensor networks[C]∥International Workshop on Wireless Ad-Hoc Networks,2004:330-334.
[7] De Berg M,Van Kreveld M,Overmars M,et al.Computational geometry[M].3rd ed.Berlin/Heidelberg:Springer,2008.
