一种重力敏感器阻尼系数测试方法*

2015-04-01贾立民

传感器与微系统 2015年12期

贾立民，吴畏，褚宁，裴闯

(天津航海仪器研究所，天津300131)

0 引言

海洋重力仪是提高舰船惯导系统精度的重要设备，主要由惯性稳定平台和重力敏感器两部分组成。重力敏感器测量重力值的方式多种多样，但采用最多的是利用弹簧伸缩来敏感重力差值的方式。目前，国际上具有代表性的弹簧式重力敏感器多采用轴对称垂直弹簧(零长弹簧)的结构，这种特有的物理结构能够将所处位置重力加速度的变化量转换为电信号，并通过线路闭环控制，从而对重力加速度进行精确测量［1～3］。由于海洋环境的特殊性，海浪对重力敏感器的干扰较为明显，为了尽可能抑制这种短周期的干扰，采用在重力敏感器内部充满阻尼液的方式。阻尼液对敏感器系统提供阻尼的大小用阻尼系数来衡量，如果阻尼系数值选取不合理，则会影响重力仪的测量精度和测量效果。因此，如何确定重力敏感器的阻尼系数并将之控制在合理范围就显得尤为重要。

本文针对充有阻尼液的强阻尼重力敏感器，提出了一种有效测量敏感器表体阻尼系数的方法。该方法通过在力矩线圈上施加不同频率的正弦激励源，从而引起敏感质量产生不同幅值正弦振荡的方式，能够较为准确地测量出敏感器弹性系统实际的阻尼系数。再选取合适粘度的阻尼液，可以将敏感器弹性系统的阻尼系数调整到所需的合理范围，有利于提高重力仪测量精度。

1 重力敏感器工作模型

德国Bodenseewerk 公司研制的KSS30/31型高精度海洋重力仪是国际上长期以来较为成熟且有代表性的重力仪，该重力仪采用轴对称结构，其核心部件是以“零长弹簧”为基础的零长金属弹簧重力敏感器［4］，其结构如图1所示。它的核心即敏感组件是由一竖直吊放的主弹簧(零长弹簧)及其悬挂的敏感质量(电容检测极板、套筒和力矩线圈等)组成，五根细金属丝控制敏感质量只能在垂直方向上作无摩擦运动。敏感质量的重力由零长弹簧来补偿，检测电容传感器能够将敏感质量的位移转换为电信号，经控制回路处理后由电磁换能器控制敏感质量回到初始零位。

图1 零长弹簧重力敏感器内部结构图Fig 1 Diagram of inner structure of gravity sensor with zero-length spring

海洋重力仪在工作时不可避免地受到海浪的干扰，海浪呈周期性且其周期远小于重力变化的周期，可以通过强阻尼和数字滤波加以抑制［5］。为了实现强阻尼，在敏感器内部充满特定粘度的阻尼液，通过调节阻尼液粘度，即可对重力敏感器的阻尼系数进行调节［6］。但敏感器的阻尼系数除了受阻尼液粘度影响外，还与敏感器自身内部结构有关。

在充阻尼液情况下，轴向阻尼力与弹簧套筒结构尺寸有很大关系，因此，在图2 中给出与阻尼计算相关的弹簧套筒简化结构示意图。

图2 中阻尼结构分为检测电容传感器区域(区域I)、弹簧套筒本体部分(区域II)、电磁换能器线圈骨架和盖板(区域III)三个部分。

下面分析这三个区域阻尼力与阻尼液性能参数和套筒结构尺寸之间关系:

1)区域I

电容检测极板侧面与检测电容传感器内壁间隙狭小，因此，在极板运动过程中随极板侧面流动阻尼液与回流阻尼液共同对电容检测极板侧面产生阻尼力。

区域I 中电容检测极板侧面阻尼力为

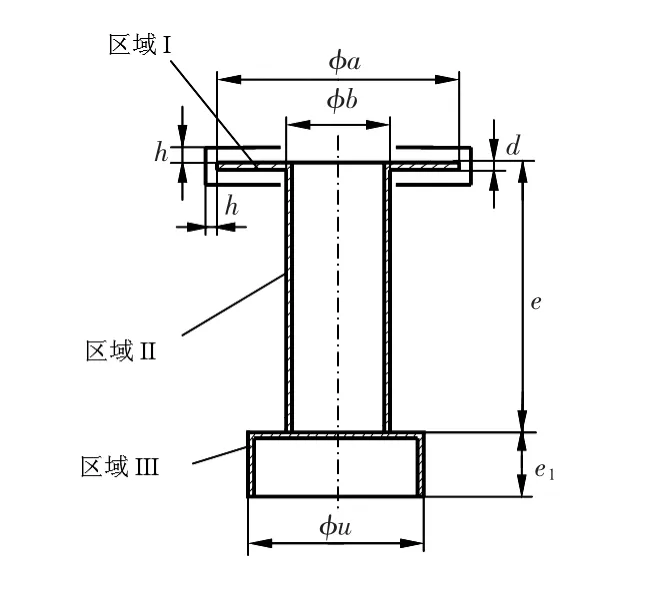
图2 阻尼系统轴向阻尼特性计算结构示意图Fig 2 Diagram of structure of damping system for calculation of axial damping properties

因电容检测极板上下面压力差产生阻力

区域I 阻尼力合力为

式中 a，b，d，h 为结构尺寸参数;μ 为阻尼液动力粘度系数;˙x 为电容检测极板沿敏感轴方向运动速度。

2)区域II

区域II 是指弹簧套筒本体部分，该区域阻尼力是由套筒与阻尼液因相对运动而产生阻尼力。弹簧套筒外阻尼液流变化层厚度为H，也就是边界层厚度，可得到阻尼力为

式中 b，e 为结构尺寸参数;H 为阻尼液在弹簧套筒上边界层厚度。

3)区域III

区域III 是电磁换能器线圈骨架和盖板构成，该部分阻尼力主要是由于盖板垂直于阻尼液液流方向，阻尼液绕流产生阻尼力是该区域主要阻尼力。绕流阻力是阻力系数cD与来流动压和迎风面积A 的乘积［8］，可表示为

综上，图2 所示阻尼结构轴向阻尼力为

在阻尼液作用下，敏感质量的移动速度很小，可忽略速度的二次项，近似认为阻尼力大小与速度值˙x 呈正比，且方向相反。因此，得到重力敏感器工作原理简化模型，如图3所示。

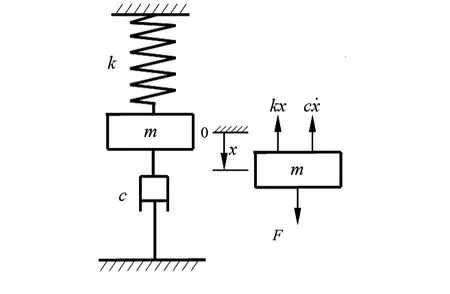
图3 重力敏感器工作原理示意图Fig 3 Working principle diagram of gravity sensor

选取重力敏感器静态稳定时敏感质量所处位置为初始零位(x=0)，此时弹簧拉力与敏感质量重力大小相等，方向相反，互相抵消后敏感质量处于稳定静止状态。敏感质量m 在干扰力F 的影响下，其运动微分方程为［9］

式中 m 为敏感质量m 的质量;c 为重力敏感器阻尼系数;k 为零长弹簧弹性系统的弹性系数。

对式(7)进行拉普拉斯变换并化简，得到敏感质量位移与干扰力的关系

2 阻尼系数测试

2.1 测试方法

利用敏感器自身结构，提出了一种在某个频段内选取不同频率激励源来实际测量重力敏感器阻尼系数的测试方法。

在与敏感质量一体的力矩线圈上施加不同频率的正弦激励信号，电磁换能器将之转换为不同频率的正弦作用力，则式(7)变为

这个方程的解分为两部分，一部分是齐次方程的解，在物理上对应的是自由阻尼振动。但这里由于施加了正弦激励信号，该方程的解应为由激励引起的特殊解，即频率与激励频率ω 相同的稳态振动。可假设特殊解具有如下形式

其中，X0为振荡的振幅，φ 为位移相对于激励F0的相位角。

将式(10)代入方程(9)，联立求解并化简为无因次形式，得到

其中，ωn为无阻尼振荡固有频率，ζ 为阻率。

图4 不同阻率的振幅—频率比曲线Fig 4 Curve of amplitude-frequency ratio with different damping coefficient

2.2 测试结果

将重力敏感器处于实际工作状态，利用信号发生器对力矩线圈施加正弦信号，激励电压幅值Ui0分别选取2，4，8 V，频率ω 在0 ～3ωn范围内选择7 个频率点(T=1.9 s，T=2.9 s，T=3.9 s，T=4.9 s，T=5.9 s，T=6.9 s，T=7.9 s，)，得到检测电容传感器经前放处理过的输出电压信号利用同一套重力敏感器装置，分别灌满两种不同粘度的阻尼液Ⅰ和Ⅱ，通过换算，得到在两种阻尼液中敏感质量振幅的实测数据如表1、表2，与理论曲线值比较如图5、图6 所示。

表1 灌阻尼液Ⅰ时输出电压测试数据Tab 1 Testing data of output voltage while pouring in damping liquidⅠ

表2 灌阻尼液Ⅱ时输出电压测试数据Tab 2 Testing data of output voltage while pouring in damping liquidⅡ

图5 质量敏感器在阻尼液Ⅰ中振幅实测数据与理论值比较图Fig 5 Comparison graph of test value and theory value of amplitude of mass sensor in damping liquidⅠ

图6 质量敏感器在阻尼液Ⅱ中振幅实测数据与理论值比较图Fig 6 Comparison graph of test value and theory value of amplitude of mass sensor in damping liquidⅡ

从图5、图6 可以看出:测试的这两种阻尼液的阻率分别为:阻尼液Ⅰ的ξ=0.25，阻尼液Ⅱ的ξ=1.35，对应的敏感器阻尼系数:阻尼液Ⅰ的c=0.17，阻尼液Ⅱ的c=0.93。综合考虑重力敏感器的使用状态和其他参数，最后选取阻尼系数为0.93 的阻尼液Ⅱ作为重力敏感器的阻尼液，再根据敏感质量m 和零长弹簧弹性系统的弹性系数k，即可确定重力敏感器表体的传递函数。