一种新的人脸图像去噪算法
2015-04-01沈千里支亚京蔡婷婷
沈千里,陈 晓,支亚京,蔡婷婷
(1.南京信息工程大学 电子与信息工程学院,江苏 南京210044;2.南京信息工程大学 大气环境与装备技术协同创新中心,江苏 南京210044)
0 引 言
图像去噪核心是去除图像噪声保护图像的细节纹理的同时提升图像质量。近年来,大数据、机器学习、字典学习、模糊滤波[1]、现场可编程门阵列(FPGA)[2]、自适应滤波[3]、各相异性扩散滤波方法[4,5]等[6~9]技术已运用到图像去噪中。
传统的空域法和小波法去噪效果不佳,特别在噪声密度大时,它们的自适应性不强。本文根据不同尺寸、大小、灰度分布的图像,提出了自适应加权向量滤波法(以下简称改进法)。
1 平滑滤波模型
1.1 标准平滑滤波模型
标准平滑滤波模型包含空域法[9,10]、频域法等,空域法包括本地滤波器和外地滤波器[11]等。标准平滑滤波模板单一,通常是N×N 邻域,邻域不允许移出边界[9],用待测像素点自身与其周边N2-1 个点取平均值后来代替原先像素点,即
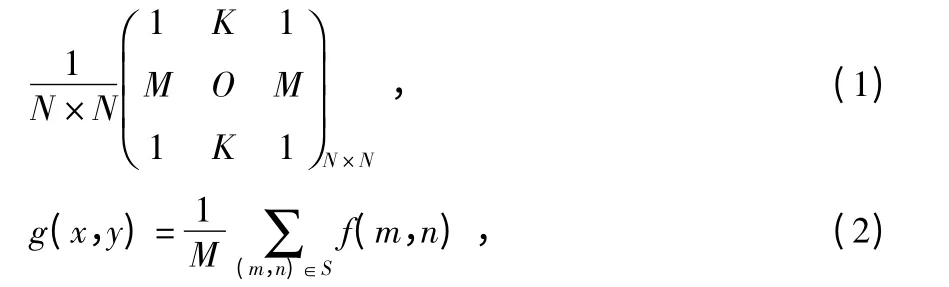
式中 S 为邻域点f(m,n)坐标集合。标准平滑滤波法是数字图像序列中一点的值,用该点的一个邻域中各点值的中值代替,即

若n 为奇数,则y 为x 序列中顺序居中的对应值;若n为偶数,则y 为x 序列中顺序居中两个数的均值。
1.2 维纳模型
维纳模型是一种基于最小均方误差的信号滤波法,使输入信号经过维纳模型处理后得到的实际输出与期望输出的误差的均方值尽可能小,从而达到滤除噪声信号的功能,即
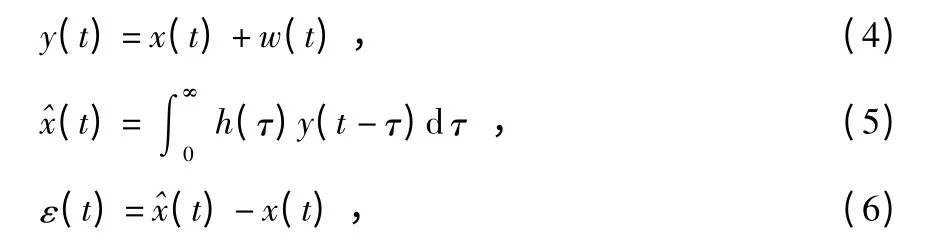
式中 y(t),x(t),w(t)分别为含噪信号、原信号、噪声信号;^x(t),h(τ),ε(t)分别为实际输出、滤波器冲激响应和误差。
2 改进法
2.1 邻域选择
相比标准平滑滤波法,改进法掩模窗口大小可设置为不同值。首先,对图像进行自适应邻域分割:定义a、b 两个尺寸掩模变量,用size 函数检测出图像的尺寸大小,长度值与高度值分别存储在m,n 两个变量中。a,b 的值可小于3,也可不等。其中,a 为掩模长度,b 为掩模高度,a,b 两个变量可以由用户在使用过程中自行选择。其次,要判断邻域变量a,b 的奇偶性,为了使得邻域更加精确,需将邻域设置的尽量小,定义两个变量k,l,即

2.2 像素扫描
式(7)和式(8)中的k 与l 分别为行循环与列循环扫描像素点的起点。定义变量:i,j 与图像像素点S(i,j),令S(i,j)为中心像素点,邻域内其他像素点以中心像素点为比较基准。两个变量i 与j 分别从k,l 开始分别循环到nk 与m-l,这样两层循环范围分别为n-2k 与m-2l,在该矩形范围内对像素点逐个扫描。定义邻域参量c,d,e,f 与子邻域横向变量i1及子邻域纵向变量j1,i1与j1分别从ik+c 与j-l+e 循环到i+l-d 与j+l-f,于是邻域的范围变成了(2k-c-d)×(2l-e-f),而标准平滑滤波法邻域范围是2k×2l,且通常k=1,因此,改进法的邻域比标准平滑滤波法小(2kl+2kf+2cl+2dl-ce-cf-de-df)个点,所以,滤波的精度更高,纹理保护也更好。然后定义number变量,在(2k-c-d)×(2l-e-f)范围内查找与S(i,j)相同的像素点S(i1,j1),若检测像素点S(i1,j1)不同于S(i,j),则number 自增1;否则,number 值不变,得到的number值就是自适应邻域内的不同于中心像素点的点数。为了方便各邻域的统计,建立一个目标矩阵Z,行数为1,列数为number,(或行数为number,列数为1),命名为Z 矩阵。然后再做一次循环,将各邻域内不同于S(i,j)的所有像素点S(i1,j1)逐个存入Z 矩阵中,每个S(i1,j1)作为Z 矩阵中的一个元素,即

或

2.3 向量加权滤波与像素点重构
Z 矩阵为一个门限阈值,用函数计算出Z 矩阵中的最大值Zmax、最小值Zmin和中值Zmed与原像素点S(i,j)比较。若S(i,j)>Zmax,同时Zmin<Zmed<Zmax,则Zmed为一个脉冲值,输出S'(i,j)=Zmed,若Zmed不是脉冲值,则S'(i,j)=Zmax;如果S(i,j)<Zmin,同时,Zmin<Zmed<Zmax,则Zmed为一个脉冲值,输出S'(i,j)=Zmed;若Zmed不是脉冲值,输出S'(i,j)=Zmin;如果Zmin<S(i,j)<Zmax,则定义一种新加权算法,即

加权因子g1,g2,g3,g4∈[0,1]。然后将所有的S'(i,j)子点组合起来,形成处理后的图像S'(i,j),即

2.4 算法流程图
改进算法流程如图1。
3 实验结果与分析
衡量图像去噪质量的客观评价有峰值信噪比(peak signal to noise ratio,PSNR)、结构相似度(structural similarity,SSIM)等。PSNR 比较图像去噪前后,值越大越好,即
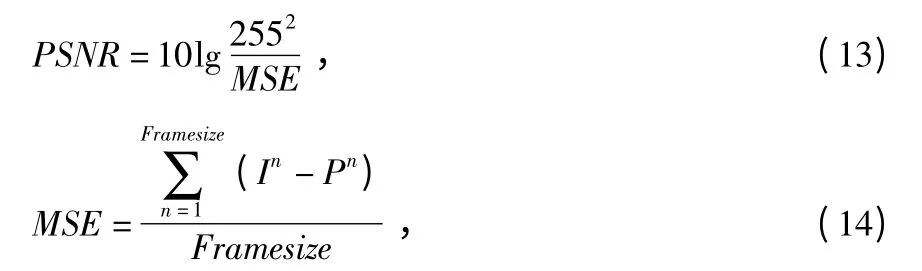
式中 Framesize 为图像尺寸。SSIM 衡量去噪后图与原图的一个相似性,SSIM∈[0,1],越接近1,则去噪后的图与原图越接近,细节保护越好。

图1 改进算法流程图Fig 1 Flow chart of the improved algorithm
给原图添加一定密度噪声,如图2,用标准平滑滤波法、维纳平滑法与改进法去噪。选取改进法中的邻域参量c=d=e=f=1。
在Zmin<S(i,j)<Zmax条件下取加权因子g1=g2=0.5,g3=g4=0,即
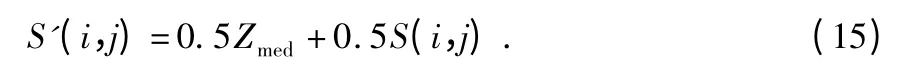

图2 原图与含噪图Fig 2 Original image and image with noise
实验1 选取σ=0.1 的含椒盐噪声图像lena.bmp(256×256,8 位)进行处理,选取3×3,4×4,5×5 作为邻域窗口,计算标准平滑滤波法、维纳平滑结合法和改进法的PSNR 与SSIM。
从图3 看出:标准平滑滤波法和维纳平滑结合法的去噪效果整体不如改进法,维纳滤波法和维纳平滑结合法去噪时未能将一些噪点滤除干净,留有噪点痕迹,而标准平滑滤波法虽滤除了噪点,但图像有明显毛刺且清晰度下降,各角点、灰度跳变点、边缘轮廓模糊化。相比而言,改进法的去噪效果佳,数据如表1。

图3 不同算法的去噪结果Fig 3 Denoising results of different algorithms

表1 各算法的客观数据统计Tab 1 Data statistics for each algorithm
从表1 看出:同等邻域下,改进法的PSNR,SSIM 值均高于标准平滑滤波法与维纳平滑结合法,在4×4 领域,改进法的PSNR 分别比标准平滑滤波法与维纳平滑结合法高8.063 9,8.764 6 dB,提升幅度明显。说明改进法的去噪程度与图像特征保护度均好于标准平滑滤波法和维纳平滑结合法。
实验2 引入漏检率[12]的概念,通过仿真得到各方法的漏检数、漏检率,如表2。

表2 各算法噪点漏检情况统计Tab 2 Noise point leak detection statistics for each algorithm
从表2 看出:改进法的漏检率远小于标准平滑滤波法与维纳平滑结合法,说明噪点滤除较彻底且检测噪声能力较强。
为了进一步强化细节纹理的保护,实验3 用canny 算子对各图进行边缘检测与提取,如图4。

表3 各算法去噪图与原图的相似度Tab 3 Similarity of denoising figure and original image of each algorithm
从表3 看出:改进法在图像特征细节的保真方面略优于标准平滑滤波法。

图4 各图的边缘检测Fig 4 Edge detection of each figure
实验4 分别给原图添加σ=0.1,0.2,0.3,0.4,0.5(10%,20%,30%,40%,50%)(噪声占全图百分比)的椒盐噪声,对比各方法的PSNR 和变化趋势,如图5。

图5 各算法在不同噪声密度下的PSNR 变化趋势图Fig 5 PSNR change trend chart of each alogrithm under different noise density
从图5 看出:在不同噪声密度下,改进法的PSNR 均高于标准平滑滤波法和平滑维纳结合法,各方法的PSNR 都随着噪声密度的增加而略有下降,但改进法的PSNR 下降速率小于标准平滑滤波法和平滑维纳结合法,噪声密度越大,改进法与平滑维纳滤波法和标准平滑滤波法的PSNR差值也越大。
4 结 论
针对传统的平滑模型在去噪过程中造成的图像模糊化和纹理失真问题,本文提出的自适应加权向量滤波法创新点在于:在用户选择滤波参量时对整幅图像进行先验测算与一个自适应分割,分析出图像的纹理和灰度分布,将重要特征点存入一个行(列)矩阵中,通过行(列)向量的最值、中值与原像素值,给出了一种加权像素重构新算法,将各点重构后合成去噪后的图。该方法尽量在像素点上与原图像素点一致,且保护了图像的清晰度。实验表明:该方法提高了人脸图像去噪效果,较彻底地滤除噪声的同时较好保护了图像纹理特征等信息,有很强的应用价值。
[1] Fabrizio Russo.A fuzzy approach to performance measurement of grayscale image denoising algorithms[C]∥Workshop on Intelligent Signal Processing(WISP),2015:1-6.
[2] 左振鹏.数字图像自适应去噪算法的FPGA 实现[J].电子技术应用,2012,38(11):14-16.
[3] 赵高长,张 磊,武风波.改进的中值滤波算法在图像去噪中的应用[J].应用光学,2011,32(4):678-682.
[4] 李金才,马自辉,彭宇行,等.基于图像熵的各向异性扩散相干斑噪声抑制[J].物理学报,2013,62(9):099501-099509.
[5] 周先春,汪美玲,周林锋.拟正态分布扩散的图像平滑[J].中国图象图形学报,2015,20(2):169-176.
[6] 付争方,朱 虹.基于模糊理论的低照度彩色图像增强方法[J].传感器与微系统,2014,33(5):121-124.
[7] Huang Dean,Kang Liwei,Wang Yuchiang Frank,et al.Selflearning-based image decomposition with applications to single image denoising[J].IEEE Transactions on Multimedia,2014,16(1):83-93.
[8] 余俊荣,何彦行,潘 丰.一种新的区域图像插值算法[J].传感器与微系统,2014,33(3):150-153,160.
[9] 贺兴华,周媛媛,王继阳,等.Matlab7.x 图像处理[M].北京:人民邮电出版社,2006.
[10]胡 旺,李志蜀,黄 奇.基于双窗口和极值压缩的自适应中值滤波[J].中国图象图形学报,2007,12(1):43-50.
[11]Shao Ling,Yan Ruomei,Li Xuelong,et al.A review and comprehensive comparison of image denoising algorithm[J].IEEE Transactions on Cybernetics,2014,44(7):1001-1013.
[12]杨柱中,周激流,郎方年.基于分数阶微积分的噪声检测和图像去噪[J].中国图象图形学报,2014,19(10):1418-1429.
