初中生代数证明水平的发展研究

陈进

摘要：数学证明具有重要的教育价值，在目前教育体制下，初中生具有怎样的数学证明水平值得大家关注。通过“日历问题”为例，对初中生的代数证明水平进行调查，了解初中生数学证明水平的一些现状，并思考出现这些状况的深层原因。

关键词：代数证明；日历问题；课程标准；性别差异；城乡差别

1.问题提出

《数学课程标准》在7～9年级的课程目标中提出“认识通过观察、实验、归纳、类比、推断可以获得数学猜想，体验数学活动充满着探索性和创造性，感受证明的必要性、证明过程的严谨性以及结论的确定性”；在课程实施建议中提出“应关注证明的必要性、基本过程和基本方法”。由此看出，新课标更加重视发展学生的数感和符号感，重视口算、估算，提倡算法多样化，更注重引导学生体会证明的必要性，理解证明的基本过程，加强培养学生“说理有据”的意识；同时，降低对论证过程形式化和证明技巧的要求，旨在让学生掌握基本的证明方法，对课程内容中有关术语在文字表达上的要求也有所降低，试图做到“淡化形式”，对于这种改变，数学界有不同的声音，孰是孰非？不敢妄下结论。在西欧和北美的一些国家，传统的数学证明在教学中的地位也在逐渐弱化。7～9年级学生的证明水平现状究竟怎么样，势必会引起许多人的关注。在八年级数学教科书下（苏科版）“说理”一节教学中的一个问题引起了我们的思考。

探索：1.当χ=-5、- 、0、2、3时，计算代数式χ2—2χ+2的值，

与同学交流。

2.换几个说再试试，你发现了什么？你能说明理由吗.

在教学中，笔者发现学生在解答本题时存在两个困难：一是代数式的值大于等于1不会归纳。二是对恒等变换证明这种形式很陌生。因此，能正确回答这个问题的学生很少。事实上，在初中阶段，几何是发展学生证明推理的主要载体。在学生的心目中，证明题就等同于几何题。众所周知，证明不仅仅局限于几何，在代数中也存在推理证明。本文以“日历问题”为例，研究7～9年级学生的代数证明发展水平。

2.研究方法

2.1 问题的设计

在数学课程标准以及在七年级数学上册（苏科版）第一章第二节中，都出现了探索月历中数量关系的问题，鉴于此问题对初中生来说都比较熟悉，便以操作，笔者略作改编，作为此次问卷调查的题目。

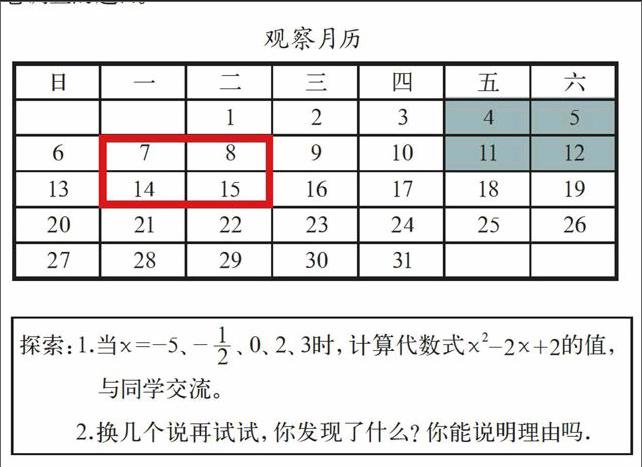
观察月历

问题1 观察月历中带有阴影方框中的4个数：

（1）方框中左上与右下数字之积为

（2）方框中左下与右上数字之积为

计算：第（1）个积与第（2）个积之差为

问题2 观察月历中另一方框中的4个数：

（1）方框中左上与右下数字之积为

（2）方框中左下与右上数字之积为

计算：第（1）个积与第（2）个积之差为

问题3 在这张月历中，将方框上下或左右平移后，方框中的4个数之间还存在如上的结论吗？说明你的理由（无论成立与否都要说明理由）。

3·调查对象

在2010～2011学年第二学期3月份在苏州常熟X校（市区公立学校、每个年级有10个班、辖区招生）每个年级随机选择了两个班级（七年级87名学生，八年级77名学生，九年级78名学生）进行了问卷测试。同时我们又在常熟M校某个（公立农村中学、每个年级有6个班、生源主要来自本镇）每个年级随机选择了两个班级（七年级、八年级、……）进行了相同的测试。

4.研究的结果

4.1 代数证明水平的划分

根据学生的回答，我们把学生的证明水平分成两类：经验的证明和逻辑的证明。经验的证明，可以划分出两个水平。

水平1通过具体的例子解释结论的真实性。

问题3在这张月历中，将方框上下或左右平移后，方框中的4个数字之间还存在如上的结论吗？请说明你的理由（无论成立与否都要说明理由）。

学生答：成立。

因为左上角的数比左下角的数小7，而且右上角的数比左上角的数大1，又因为右上角的数比左下角的数小6，左上角的数比右下角的数小8，所以应该积小7。

第二类是演绎的证明，利用代数式的恒等变换获得一般结论。此时，学生的水平存在以下三个水平。

水平3用字母来表示数，但未达到水平4。

问题3在这张月历中，将方框上下或左右平移后，方框中的4个数字之间还存在如上的结论吗？请说明你的理由（无论成立与否都要说明理由）。

学生答：存在。

上下两个数之差为7

问题3在这张月历中，将方框上下或左右平移后，方框中的4个数字之间还存在如上的结论吗？请说明你的理由（无论成立与否都要说明理由）。

学生答：成立。

设左上角的数为χ，右上角的数为χ+1，左下角的数为χ+7，右下角的数为χ+8，

则：χ（χ+8）-（χ+1）（χ+7）=χ2+8χ-（χ2+8χ+7）。

问题3在这张月历中，将方框上下或左右平移后，方框中的4个数字之间还存在如上的结论吗？请说明你的理由（无论成立与否都要说明理由）。

学生答：成立。

设左上角的数为n，右上角的数为n+1，左下角的数为n+7，右下角的数为n+8，

则：左上与右下之积为n2+8n，

右上与左下之积为n2+8n+7，

差为7。

所以成立。

4.2 数据分析

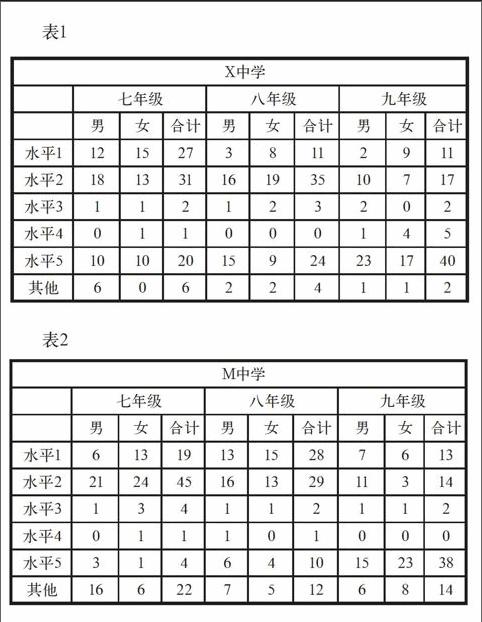
第一，数据表明（如下页表1、表2）能用字母表示数来解决问题（也就是达到水平3以上）的人数偏少，X中学学生七年级占26.44%，八年级占35.06%，九年级占61.04%；M中学学生七年级占9.47%，八年级占15.85%，九年级占49.38%。

第二，学生的代数证明水平七、八两个年级之间无显著差异，九年级显著高于其他两个年级。X中学三个年级之间存在显著性的差异（χ2（10）=33.530， p=0.000）；七年级、八年级无显著差异（χ2（5）=8.364， p=0.137）；八年级、九年级有显著差异（χ2（5）=16.097， p=0.007）；七年级、九年级有显著差异（χ2（5）=21.624， p=0.001）。X中学三个年级之间存在显著性的差异（χ2（10）=64.775， p=0.000）；七年级、八年级无显著差异（χ2（5）=10.464， p=0.063）；八年级、九年级有显著差异（χ2（5）=28.202， p=0.000）；七年级、九年级有显著差异（χ2（5）=47.569， p=0.000）。

第三，学生的代数证明水平存在城乡差别。七年级（χ2（5）=24.141，p=0.000）；八年级（χ2（5）=18.799，p=0.002）；九年级（χ2（5）=14.416，p=0.013）。

第四，每个年级的性别之间无显著差异，整个参与调查的对象的性别之间无显著差异。X中学三个年级的男女生之间均无显著差异，七年级χ2（5）=7.626，p=0.178；八年级χ2（4）=4.253，p=0.373；九年级χ2（5）=9.673，p=0.085，M中学三个年级的男女生之间均无显著差异；七年级χ2（5）=10.315，p=0.067；八年级χ2（5）=1.757，p=0.882；九年级χ2（4）=6.607，p=0.158。

5.讨论

5.1 学生代数证明水平的发展受到了课程教材的影响

初三学生能从数学的角度提出问题、理解问题，并能综合运用所学的知识和技能解决问题，发展应用意识；形成解决问题的一些基本策略，体验解决问题策略的多样性，发展实践能力与创新精神。同时教材对“空间与图形”的主要关注点—推理与证明，进行了整体性设计，这些设计主要基于以下两点考虑：一是合情推理与演绎推理是相辅相成的两种推理形式，不是隔立的，更不是对立的，应当把它们有机地结合起来。二是数学教学需要形式化训练，但过早地形式化可能会使学生远离数学的本质。推理的本质是“有条理的思考和表达”，而不是：“∵……∴……（……）”的形式化证明。我们的调查时间是在第一学期，而教材把证明放在八（下）和九（上），从这个角度来看也表明课程有效地促进了学生逻辑性证明的发展。

5.2 数学代数证明水平与学生的性别差异有关系

1993年，国际数学教育委员会（ICMI）在瑞典专门召开过“性别与教育”国际研讨会，几名美国学者通过对部分小学老师的深入调查分析，认为在数学学习上确实存在着性别差异，而且这种差异随年级的升高逐渐增大，越是高认知水平的学习，男生的优秀就越明显。我国学者在这方面的研究结论大致有两类：一类认为，男、女两性的数学思维发展在总体上是平衡的，但在逻辑推理、掌握逻辑法则、辩证思维及空间想象等方面的表现，又是各具特色的；另一类则认为，男、女两性的数学学习水平在总体上有显著差异（个别差异不显著除外），男性要高于女性。通过这次调查，发现在初中数学证明水平方面男女学生几乎没有差异，原因可能是在经济相对发达的苏南地区，家庭、社会和学校对性别基本已无偏见，对男女生的期望值是一样的；在对数学成绩的要求上，家长和教师对男女生是相同对待；平时在学校教学中，教师对男女生要求是相同的，环境因素的影响已经很小了。

5.3 数学代数证明水平与家庭教育有关

家长也对“教育孩子”给予了很大的关注，对孩子的健康成长起到了越来越大的积极作用。但由于长期以来的城乡二元结构，导致城乡之间经济、文化发展不平衡，表现在教育上城乡还存在着一定的差距。从这次调查结果来看也符合了这一点，本次调查的两所学校从硬件设施和师资及教学内容上来看基本不存在差异，可能主要在于家庭教育上的差异：一是经济状况影响，为了给孩子提供更好的学习和生活环境，大部分的农村家长将更多精力用在工作上，很少有时间关心学生的课余生活。二是资料表明，农村人口比城镇人口受文化教育年限平均少2～3年，城镇居民再学习提高的时间和机会多。农村家长接受的教育较少，文化程度普遍偏低，相对缺乏自我约束力和调节力，从而给子女造成一定的影响。