ARIMA模型在居民消费价格指数预测中的应用研究

杨鸿雁

摘 要：居民消费指数是监测和调控价格总水平、决策与分析宏观经济、核算国民经济的主要指标。文章将最近几年来的相关数据收集起来，运用相关函数构建了一个ARIMA模型，同时借助Eviews软件预测出相关参数。通过分析这个模型能够合理预测出我国居民消费价格指数。

关键词：ARIMA模型 居民消费价格指数 应用

中图分类号：F014.5 文献标识码：A

文章编号：1004-4914（2015）03-062-03

居民消费价格指数是市场价格的真实反映，它不仅能够反映出某一时段通货膨胀程度，而且反映了国民经济缩减程度。国家财政、社会保障、消费、价格、货币、工资等政策均受到居民消费价格指数的影响，同时，居民消费水平及评价也受到了其影响。居民消费价格指数预测可以有效引导价格舆论，有助于提高价格调控总体水平；同时可以正确指引合理消费价格的形成、满足各种需求，有助于稳定市场价格信息秩序和日常经济生活。例如，目前交通、教育、医疗等垄断行业价格增长迅速，造成居民储蓄过量，抑制了正常消费，消费结构不合理，阻碍了经济的可持续发展；而精准的居民消费价格指数预测能帮助国家相关部门有效利用价格与其他经济手段，达到调控价格总水平的目标。所以，准确分析与预测居民消费价格指数十分必要。

一、相关概念

（一）居民消费价格指数

居民消费价格指数一直都是政府和社会大众高度重视的社会热点问题，这主要是因为其同人们日常生活密切联系。居民消费价格指数是一个可预见的一段时间内人们支付的程度，深刻影响着消费商品和服务的价格的变动情况。分析和预测居民消费价格指数一直都是经济学研究的重点，正确地分析与预测物价指数是制定科学合理的经济政策的基础。

（二）ARIMA基本理论与方法

时间序列分析其实是一种比较常见的的数量分析方式，其重点阐述和描绘事物随着时间的变化而数量出现规律性变化。近年来，国内大量研究人员基于这一领域进行了深入的研究，并构建了相对应的时间序列。预测对象随着时间的推移组建成一个全新的序列数据，其随机性较强，利用数学模型来全面反映出这个序列的真实内涵。只要能够正确认识和分析这一模型便可以从时间序列值角度预测出该序列的未来趋势。

二、非平稳时间序列分析模型（ARIMA模型）

（一）平稳时间序列模型

ARMA模型也被称为自回归移动平均模型。同时被划分为MA模型、AR模型和ARMA模型三种类型。

AR模型也叫做p阶自回归模型，简称AR（p），其结构模型如下：

x1=φ0+φ1xt-1+……+φpxt-p+εt，φp≠0，E（εt）=0

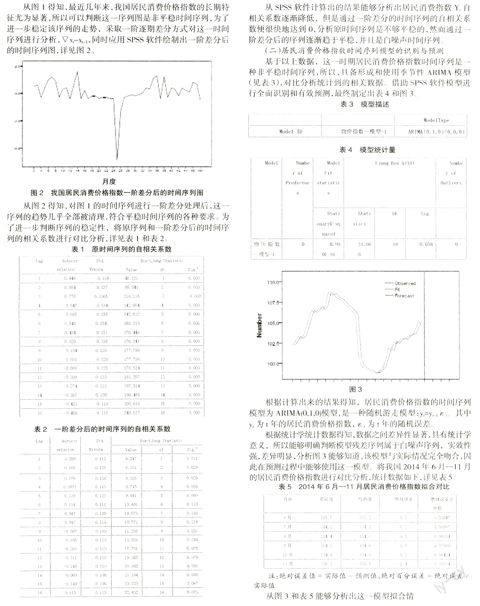
Var（εt）=σ2ε，E（εtεs）=0，S≠t，Exsεt=0，？坌s

MA模型被称为q阶移动平均模型，简称为MA（q），其模型结构如下：

xt=μ+εt-θ1εt-1-θ2εt-2-……-θqεt-q

θq≠0

E（εt）=0，Var（εt）=θ2ε，E（εtεs）=0，s≠t

ARMA模型也被稱为自回归移动平均模型，简称ARMA（p，q），其模型结构如下：

xt=φ0+φ2xt-1+φ2xt-2+……φpxt-p+εt-φ1εt-1-……-φqεt-q

φp≠0，φq≠0

E（εt）=0，Var（εt）=σ2ε，E（εtεs）=0，s=t

Exsεt=0，？坌s

引入延迟算式，ARMA（p，q）模型简称为：

φ（B）xt=θ（B）εt

式中：φ（B）=1-φ1B-……φpBp，为p阶自归系数多项式；θ（B）=1-θ1B-……-θqBq，是q阶移动平均系数多项式。

因此，当q=0时，ARMA（p，q）模型便成为了AR（P）模型；当p=0时，ARMA（p，q）模型则演变成为了MR（q）模型。

（二）非平稳时间序列分析模型（ARIMA模型）

ARIMA（p，d，q）模型的结构为：

φ（B）？荦dxt=θ（B）εt

E（εt）=0，Var（εt）=σ2s，E（εtεs）=0，s≠t

Extεs=0，？坌s

其中：？荦d=（1-B）d；{εt}是零均值白噪声序列：φ（B）=1-φ1B-……-φpBp是平稳可逆ARMA（p，q）模型的自回归系数多项式；θ（B）=1-θ1B-……-θqBq是平稳可逆ARMA（p，q）模型的移动平滑系数多项式。

显然，如果d=1，p=q=0时，AMIMA（0，1，0）模型便是xt=xt-1+εt，这一模型便称为随机游走模型或醉汉模型。

三、基于ARIMA的居民消费价格指数模型

居民消费价格指数是全球各国都十分重视和编订的一种指数，它充分反映了市场价格的总体趋向，是政府制定工资政策和价格政策的主要参考信息，所以正确分析与预测物价指数也是制定准确的经济政策的关键。本文以2011—2014年我国居民消费价格指数的相关数据为例，从整体上分析和预测我国将来的居民消费价格指数。

（一）数据分析及预处理

基于整理而来的样本数据，采用SPSS 软件制定出有关时间序列图。详见图1。

从图1得知，最近几年来，我国居民消费价格指数的长期特征尤为显著，所以可以判断这一序列图是非平稳时间序列，为了进一步稳定该序列的走势，采取一阶逐期差分方式对这一时间序列进行分析，？荦xt-xt-1，同时应用SPSS软件绘制出一阶差分后的时间序列图，详见图2。

从图2得知，对图1的时间序列进行一阶差分处理后，这一序列的趋势几乎全部被清理，符合平稳时间序列的各种要求。为了进一步判断序列的稳定性，将原序列和一阶差分后的时间序列的相关系数进行对比分析，详见表1和表2。

从SPSS软件计算出的结果能够分析出居民消费指数Yt自相关系数逐渐降低，但是通过一阶差分的时间序列的自相关系数便很快地达到0，分析原时间序列是不够平稳的，然而通过一阶差分后的序列逐渐趋于平稳，并且是白噪声时间序列。

（二）居民消费价格指数时间序列模型的识别与预测

基于以上数据，这一时期居民消费价格指数时间序列是一种非平稳时间序列，所以，具备形成和使用季节性ARIMA模型（见表3），对比分析统计到的相关数据。借助SPSS软件模型进行全面识别和有效预测，最终制定出表4和图3。

根据计算出来的结果得知，居民消费价格指数的时间序列模型为ARIMA（0，1，0）模型，是一种随机游走模型：yt=yt-1εt。其中yt为t年的居民消费价格指数，εt为t年的随机误差。

根据统计学统计数据得知，数据之间差异性显著，具有统计学意义，所以能够明确判断模型残差序列属于白噪声序列，实效性强，差异明显，分析图3能够知道，该模型与实际情况完全吻合，因此在预测过程中能够使用这一模型。将我国2014年6月—11月的居民消费价格指数进行对比分析，统计数据如下，详见表5。

从图3和表5能够分析出这一模型拟合情（下转第65页）（上接第63页）况良好，能够准确地预测出我国居民消费价格指数。预测结果详见表6。

（三）结果分析

分析图3得知，我国居民消费价格指数从2011年以来呈上涨趋势，同时上涨速度较快，到2012年4月达到顶峰。这是因为2010年以来国家经济水平不断提升，财富效应较强，在很大程度上促使我国居民消费价格指数不断增长。

这一模型对2014年1月—5月的居民消费价格指数进行了预测，结合相关调查数据得知，前四个月的预测趋势同实际情况相一致，我国2014年1月—5月的居民消费价格指数在不断的上漲。由于居民消费价格指数不断上涨，基于这样的形势，需要政府制定有效的宏观政策进行调控，将物价控制在一个合理范围内。

时间序列分析的ARIMA模型预测问题，其真实内涵为经过分析研究社会经济发展变化状况，发现与总结出其发展变化的规律，基于此来预测经济状况的将来。预测过程中不得受到其他因素的干扰，只是关注序列自身，构建科学合理的模型进行分析预测，这能够从源头上避免查找主要因素和识别主要因素与次要因素的难度；相比于回归分析法，其能够有效解决在查找因果模型中对随机干扰的限定条件在经济活动中无法满足的问题。从而，这些便是ARIMA模型预测同其他预测方式不同之处，也是其优势所在。

本文基于我国2010—2014年实际居民消费价格指数，构建了ARIMA的物价指数预测模型。从本文研究结果得知，这一模型的实际值和拟合值的百分比绝对误差、绝对误差均较小，基本上可以忽略，所以拟合效果良好，从而能够科学合理地模拟和预测我国居民消费价格指数的变化情况，其应用价值大。

参考文献：

[1] 刘春燕，姚杰.时间序列分析在居民消费价格指数预测中的应用[J].现代商贸工业，2010（16）

[2] 李嫣怡，刘荣，丁维岱.EViews统计分析与应用[M].北京：电子工业出版社，2013

[3] 薛冬梅.ARIMA模型及其在时间序列分析中的应用[J].吉林化工学院学报，2010（3）

[4] 赵喜仓，周作杰.基于SARIMA模型的我国季度GDP时间序列分析与预测[J].理论新探，2010（22）

[5] 蒋和.基于ARMA模型的恩格尔系数的分析与预测[J].理论经济学，2013（8）

（作者单位：中共辽源市委党校 吉林辽源 136200）（责编：贾伟）