采用DCT稀疏表示与Dual-PCNN的图像融合算法

宋 斌，吴乐华，唐晓杰，文玉强，牟宇飞

采用DCT稀疏表示与Dual-PCNN的图像融合算法

宋 斌，吴乐华，唐晓杰，文玉强，牟宇飞

（重庆通信学院，重庆 400035）

针对已有图像融合方法会导致融合图像亮度不均匀，与原图像对比度不一致，不适合人眼视觉效果的缺点，提出将DCT稀疏表示与双通脉冲耦合神经网络相结合的压缩感知域图像融合算法。首先结合图像DCT稀疏表示的特点，设计射线采样矩阵；再对测量值采用基于测量值的信息熵加权平均融合；最后经过全变分优化算法对融合测量值重构得到融合图像。通过对多组不同类型传感器所获图像融合实验的主观视觉分析和客观评价表明，该算法所得的融合图像能从原始图像中获取更多有用信息，更好地保持原图像的边缘信息，从而获得更好的视觉效果。

压缩感知；双通道脉冲耦合神经网络；信息熵；全变分优化算法

0 引言

图像融合技术是在不引入额外信息的前提下，将包含在多幅源图像中的重要信息融合起来，得到一幅包含信息更丰富的图像的技术[1]，它在计算机视觉、遥感、医学以及军事领域都有着广泛的应用前景。伴随着多媒体通信技术的发展及各种类型传感器的使用，图像融合所需处理的数据量越来越大，对传输硬件提出了更高的要求，同时也给图像融合技术本身的发展带来不利影响。2006年，E. Candse，D. L. Donoho以及T. Tao等人提出了一种新的信息获取指导理论——压缩感知理论（Compressed Sensing，CS）[2-4]，该理论表明：若信号在某个变换域是稀疏的或可压缩的，就可以利用与变换矩阵非相干的测量矩阵将变换系数投影为低维观测向量，这种投影保持了重建信号所需的信息，通过进一步求解稀疏最优化问题就能够从低维观测向量精确地或高概率精确地重建原始高维信号。CS理论提出以后就被迅速应用于图像融合领域，有效地解决了多传感器所获取的大量图像信息，给存储和传输硬件设备所带来压力的问题，同时也让图像融合算法能使用尽可能少的数据完成图像融合，大大提高融合算法的效率。

脉冲耦合神经网络（Pulse Coupled Neural Networks，PCNN）是Eckhorn等人通过模拟猫的大脑视觉皮层中同步脉冲现象提出的模型[5]，该神经网络具有全局耦合性和脉冲同步性的特征。Broussard等人[6]首先将PCNN应用于图像融合中，证实了PCNN无需经过训练，就能够从复杂的背景下提取有效信息。文献[7]针对图像DCT的频谱特性，提出了一种放射状的采样模式，通过新采样模式构造测量矩阵，并在此基础上提出了一种基于DCT稀疏的压缩感知域图像融合方法，该方法将得到的测量值进行小波变换，通过加权平均计算得到近似系数和细节系数，再经过IDWT变换得到融合测量，最后采用梯度投影稀疏算法（Gradient Projection For Sparse, GPSR）重构得到融合图像，该算法取得一定的效果，但是算法复杂度过高，而且对原图像的信息获取不够充分。

融合规则的选取同样严重影响融合效果。文献[8]采用基于测量值最大的融合规则，该方法在融合过程中带入较多的噪声，重构后的图像出现明显的条纹现象；文献[9]采用基于测量值平均的融合规则，文献[10]采用基于测量值标准差的融合规则，这些融合规则都没有充分考虑CS测量值的数据特点。

综合CS理论和PCNN的特点，提出一种基于CS理论和Dual-PCNN的图像融合算法。采用DCT变换对多传感器图像进行稀疏表示，并针对DCT变换后的数据特点，设计了射线（Radial）采样矩阵，结合测量值的特点提出基于测量值信息熵（Information Entropy，IE）的加权融合规则，最后通过更加适合二维图像重构的全变分优化（Total Variation，TV）算法[11]实现对融合后图像的重构。仿真实验结果的主观分析和客观评价表明：本文的融合方法能够从原图像中获取更多信息，使融合图像更加适合人眼的观察。

1 基础知识

1.1 压缩感知理论

设一个实值、有限长的一维离散信号，可视为()∈R中的一个×1列向量（＝1, 2, …,）。假设信号可表示为：

＝(1)

式中：是×基向量矩阵。若只包含个非零向量，则称是稀疏[4]。通过＝得到压缩测量值，其中∈R，是×测量矩阵，可得：

＝＝Q(2)

虽然从＜的测量值中恢复是一个病态问题，但是若满足限制性等距特性，则可以通过优化过程精确恢复稀疏信号。

1.2 Dual-PCNN模型

双通道脉冲耦合神经网络（Dual-channel Pulse Coupled Neural Network, Dual-PCNN）模型是PCNN的一种改进模型，克服了单通道PCNN模型只能对单张图像进行特征提取的不足，能有效实现对多幅图像的同时融合[13]。

若把图像中某像素的坐标记为(,)，则Dual-PCNN模型可作如下描述：

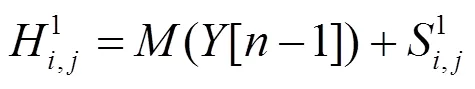
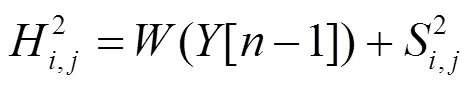
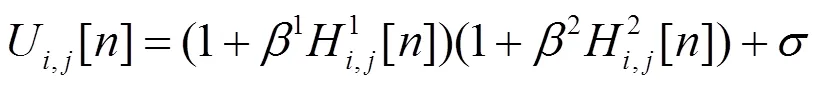
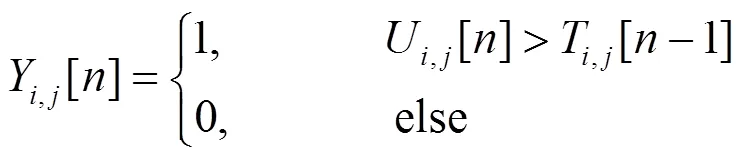
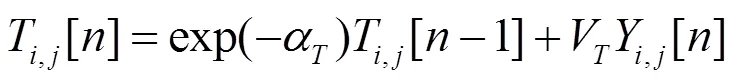
式中：H,j（＝1, 2）代表从外部输入的对称神经元通道；(×)和(×)代表从周围神经元到当前神经元的导入函数；U,j代表内部状态神经元；∈[0, 1]是权重参数，用来表示第个通道的重要性，通常情况下取1＝2＝0.5；是一个水平因子；T,j是决定触发的动态阈值；和V分别为时间常数及归一化常数；表示迭代的次数。

Dual-PCNN模型如图1所示，主要由3个部分组成：信息采集、信息融合和脉冲发生器。信息采集部分能够接收来自神经元的2个以上的信息触发，信息融合部分主要进行待融合图像信息的融合，脉冲发生器则负责产生对信息采集单元的触发脉冲。

2 采用DCT稀疏表示和Dual-PCNN的CS图像融合

2.1 DCT稀疏和双射线采样矩阵

采样矩阵的设计对图像重构的质量十分重要，由于多传感器图像经过DCT稀疏变换后，其信息主要集中在左上角部位，如图2(b)所示。本文针对多传感器图像经过DCT稀疏变换后的这一特点设计Radial采样矩阵，该矩阵明亮的地方为采样部分，数值为1；黑暗的地方为舍弃部分，数值为0。该采样矩阵与随机采样矩阵相比，在采样获取相同数据量的同时，能够获得更多有用信息。

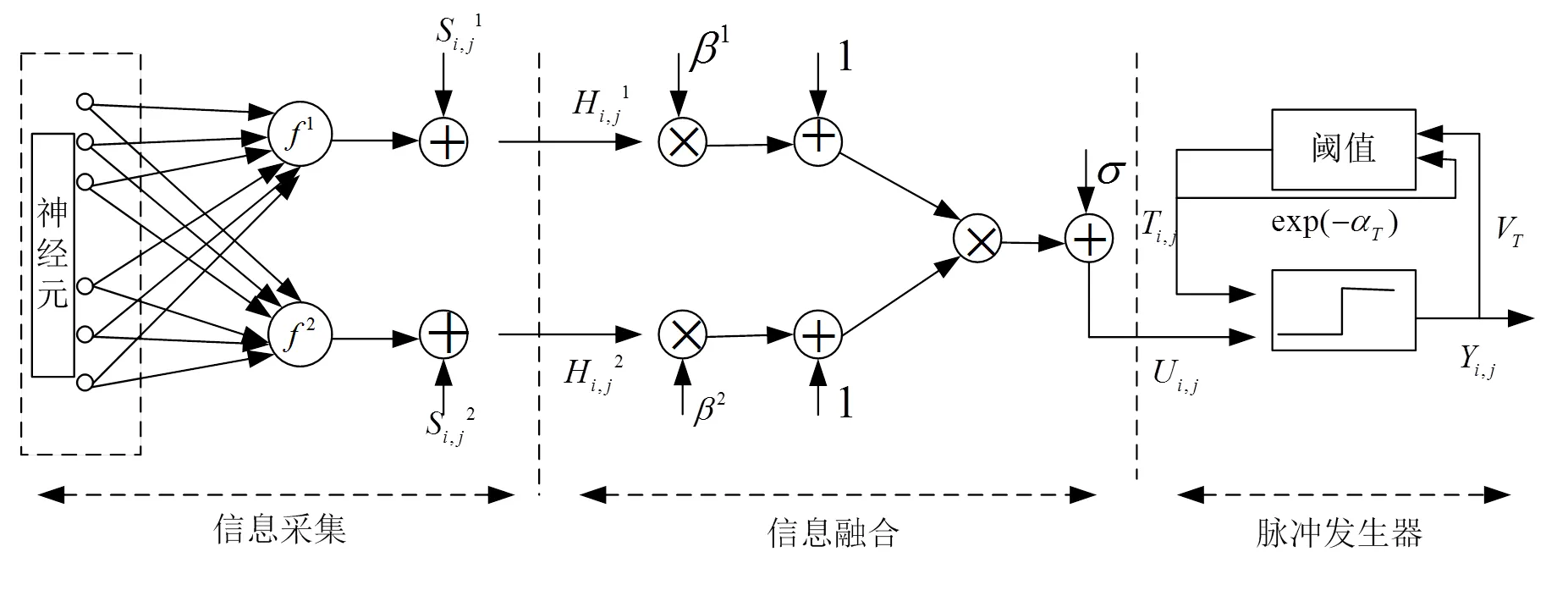
图1 Dual-PCNN模型

图2 原图、DCT稀疏表示及Radial采样矩阵图

2.2 基于测量值IE加权融合规则

基于测量值的信息熵加权融合，是通过计算测量值的信息熵来确定融合的权重系数。其数学表达式如下：

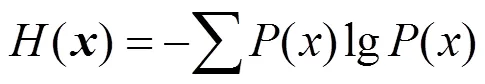
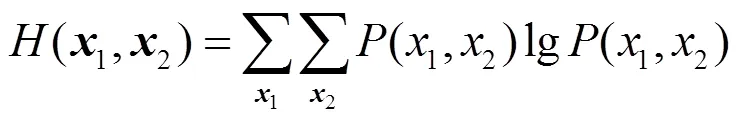
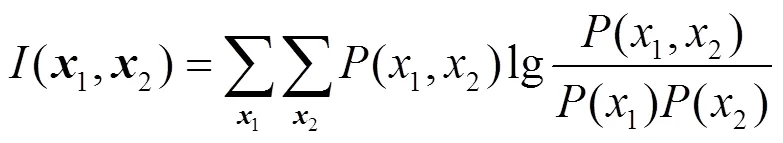
据此，测量值的融合权重系数可以用下列数学表达式：

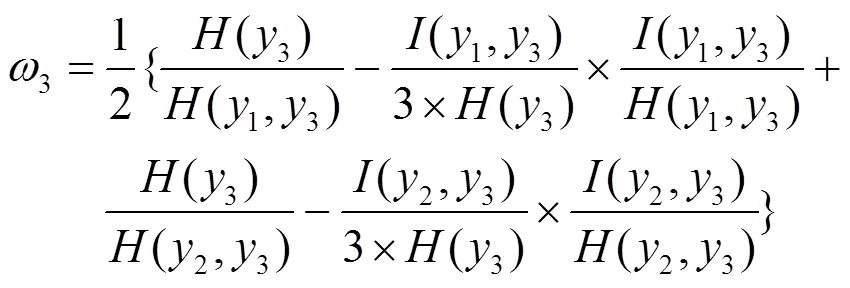
这样构造融合权重系数，可以充分发挥各个测量值的信息熵以及互信息熵，在融合权重中的作用。

2.3 全变分优化（Total Variation, TV）算法

重构算法同样是CS理论的核心之一，即从维测量值恢复维原始信号的过程，

其中远大于。目前，常用的重构算法主要有匹配追踪（matching pursuit, MP）系列算法和最小L1范数法等。MP系列算法包括正则正交匹配算法、正交匹配算法、压缩采样匹配追踪算法等，该系列算法对于小尺度信号重构较为理想，但对于大信号特别是有噪声存在的情况下，重构结果不够准确，而且算法本身的鲁棒性不强[14-15]；最小L1范数法比较适合一维信号的重构[16]。Candes E、Tao T和Schmidt M等人从大量的自然图像离散梯度都是稀疏的这一事实出发，总结出如下更加适合二维图像重构的TV算法[11,17]，其算法模型为：

MinTV()

Subject to||－||≤(14)

式中：函数TV()为图像离散梯度的和，该方法对二维图像的重构质量更高，算法本身的鲁棒性更好。

2.4 算法实现

本文具体算法的实现主要分为以下几步：

Step1：将原图像、及经过Dual-PCNN的信号进行DCT稀疏变换

＝(1,2, …,a)(15)

＝(1,2, …,b)(16)

＝(1,2, …,c)(17)

Step2：对经过DCT变换后的系数采用双射线采样矩阵计算、、的测量值

＝(1,2, …,x)＝(18)

＝(1,2, …,y)＝(19)

＝(1,2, …,z)＝(20)

Step3：计算融合后的测量值＝(1,2, …,f)

＝1×＋2×＋3×(21)

Step4：利用通过最小全变分方法重构融合图像¢

MinTV(¢)

Subject to||¢－||2≤(22)

3 仿真实验及结果分析

为验证本文算法的有效性，采用3组不同类型传感器获取的已经配准好的大小为256×256的图像进行融合实验，并与基于小波变换的融合方法（Wavelet），文献[8]的融合方法（CS-Max），文献[9]的融合方法（CS-Mean）以及文献[10]的融合方法（CS-SD）进行对比。为了方便表述，将本文方法记为CS-PCNN-IE。试验中，Dual-PCNN模型的参数选取如下：＝1，T,j为与输入图像大小相同的单位矩阵，、V分别取为0.012与3000，迭代次数为10，采样率均采用30%。第一组实验针对可见光图像与红外图像进行融合，结果如图3所示；第二组实验针对计算机X线断层扫描（Computed Tomography，CT）图像和磁共振（Magnetic Resonance Imaging，MRI）图像进行融合，结果如图4所示；第三组实验针对多焦点图像clock A、clock B进行融合，结果如图5所示。

由图3～图5可以看出，在3组实验所得的融合图像中，用Wavelet方法融合后的图像轮廓不是很清晰，特别是在对医学图像及多焦点图像进行融合时，存在明显的边缘模糊现象；CS-Max算法融合后所得图像有明显的条纹现象，尤其是对医学图像进行融合后图像有明显的白色阴影，这是由于采用最大值融合规则时带入的噪声较多引起的；CS-Mean算法和CS-SD算法所得的融合图像质量差别不大，均有效提高了融合图像的清晰度，并有效抑制了噪声，但与原图像相比，融合图像明显太亮；与CS-Mean算法、CS-SD算法相比，本文提出的CS-PCNN-IE算法所得融合图像的亮度分布更加均匀，更加适合人眼的视觉感受。

表1为信息熵（Information Entropy，IE）、互信息（Mutual Information，MI）[17]以及相关系数（Correlation Coefficient，CC）[18]3个客观评价指标的对比结果。其中，熵越大说明融合图像所含的信息量越多，图像的融合效果越好；互信息越大说明从原图像中获得的信息越多，图像融合效果越好；相关系数越接近1说明图像融合越好。

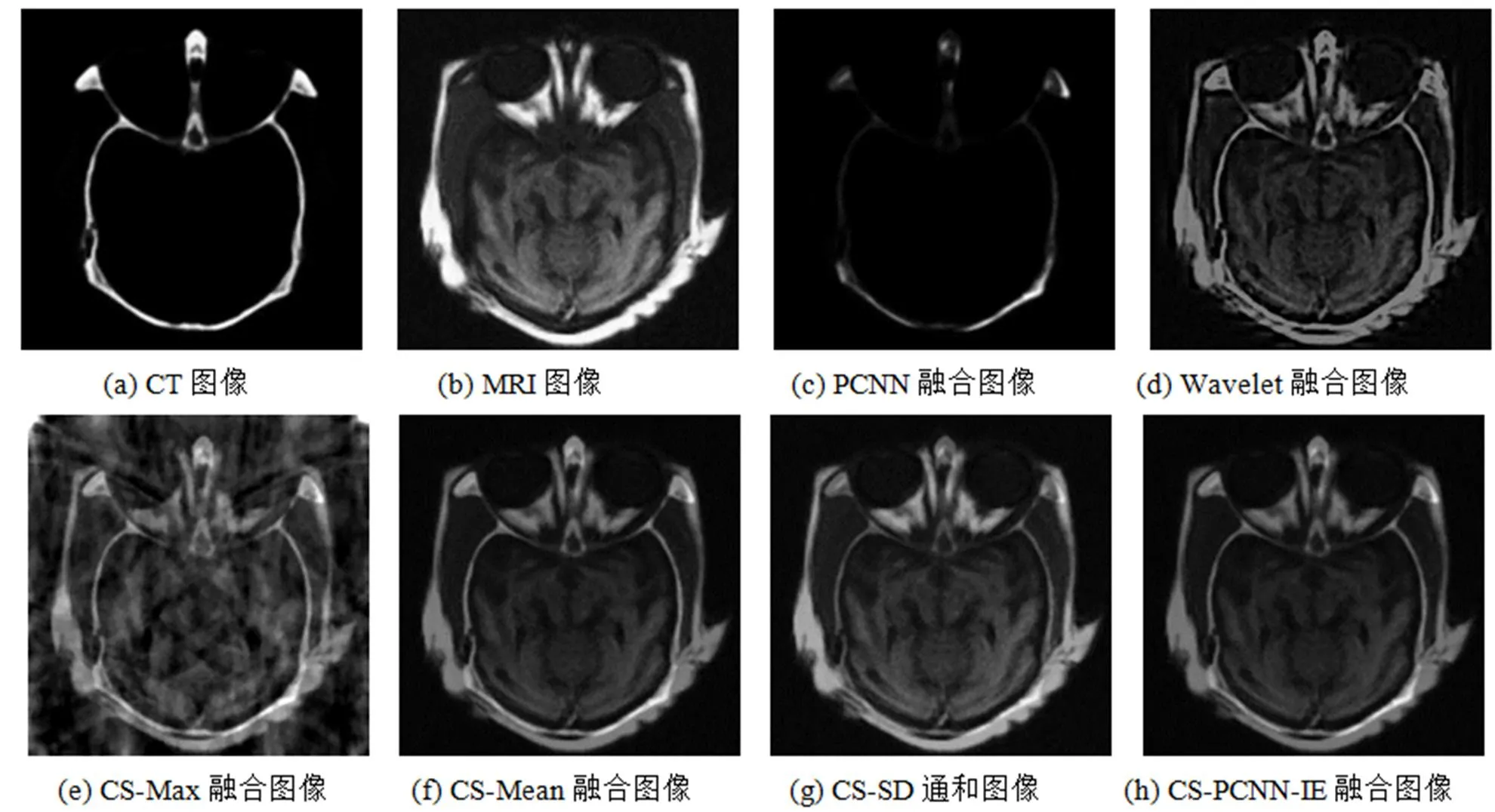
图4 第二组图像仿真结果

图5 第三组图像仿真结果

从表1的统计数据可知，CS-Max融合算法由于在融合过程中带入较多噪声，所以IE值在每组实验中都是最大，排除CS-Max融合算法，则实验结果中IE最大值第一组和第三组是CS-Mean融合算法；第二组是CS-SD融合算法。实验结果中MI最大值第一组和第三组是本文算法CS-PCNN-IE，第二组是CS-SD融合算法。实验结果中CC最大值第一组是CS-Mean融合算法，第二组是CS-SD融合算法，第三组是本文算法CS-PCNN-IE。主客观评价表明：本文算法结合CS与Dual-PCNN模型，能够有效地从原图像中获得更多的信息，特别是在对多焦点的图像进行融合时，在很好保持图像边缘信息的同时大大丰富了融合后图像所获得的信息。

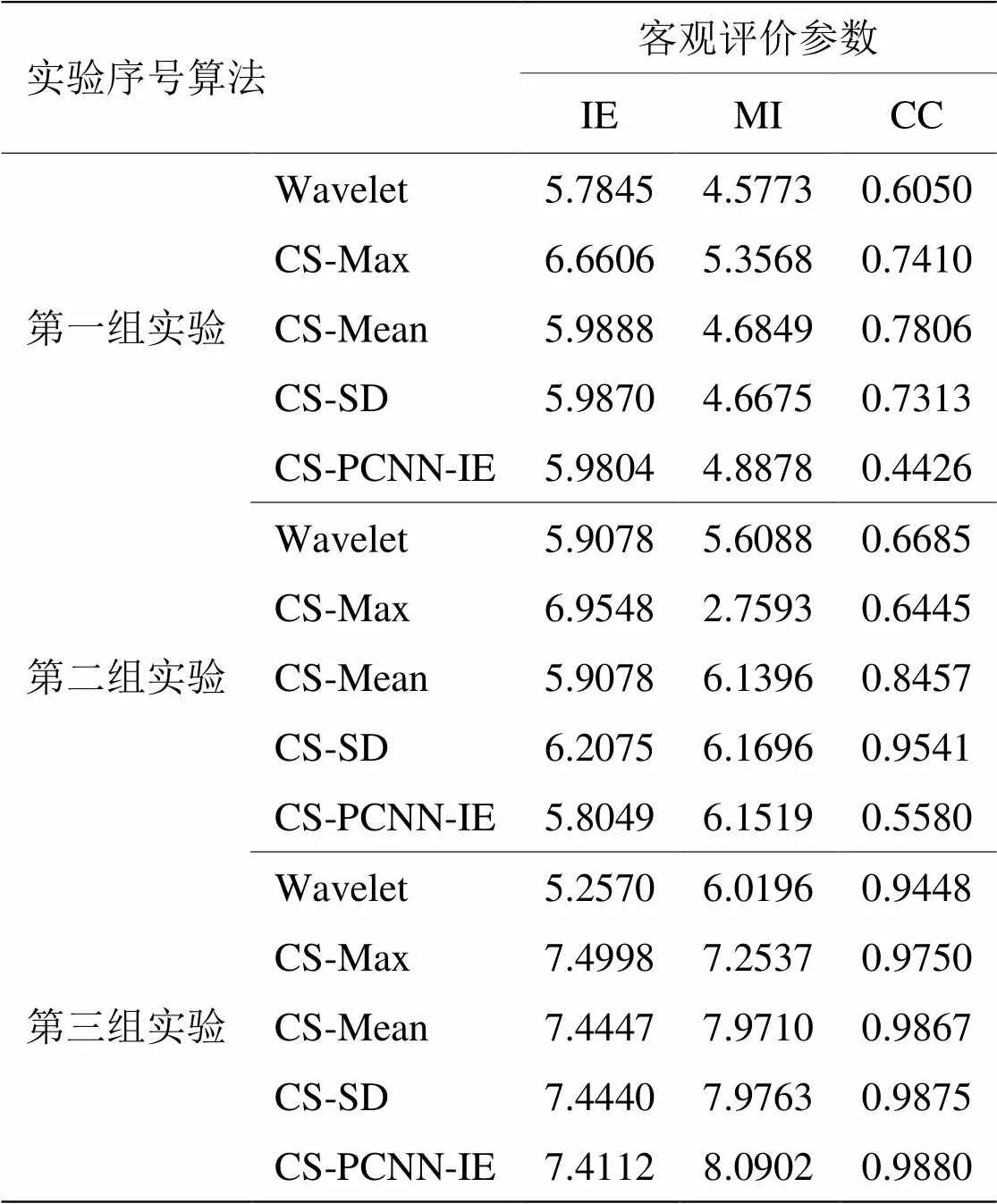
表1 各融合方案的评价参数统计

4 结束语

本文提出了一种结合Dual-PCNN模型与CS理论的不同传感器获取图像的融合方法，该方法针对DCT稀疏表示的系数特点，采用一种在射线采样模式下基于测量值信息熵的测量值加权融合方法，通过最小全变分（TV）算法实现融合后测量值的图像重构。仿真实验表明：本文提出的融合算法能够有效实现图像融合，融合后的图像更加适合人眼的观察，为进一步研究CS域的图像融合方法提供了参考。

[1] Parmar K, Kher R. A. Comparative analysis of multimodality image fusion methods[C]//(),, 2012: 93-97.

[2] E. Candes, T. Tao. Near optimal signal recovery from random projections：universal encoding strategies[J]., 2006, 52(12): 5406-5425.

[3] E. Candes. Compressive sampling[C]//P, 2006: 1433-1452.

[4] D. L. Donoho. Compressed sensing[J]., 2006, 52(4): 1289-1306.

[5] Eckhorn R., Reiboeck H. J., Arndt M., et al. Feature linking via synchornization among distributed assemblies:simulation of results from cat cortex[J]., 1990(2): 293-307.

[6] Broussard R. P., Pogers S. K., Oxley M. E., et al. Physiologically motivated image fusion for object detection using apulsecoupled network[J]., 1999, 10(3): 554-563.

[7] Juanjuan Han, Otmar Loffeld, Klaus Hartmann, et al. Multi image fusion based on compressive sensing[C]//(),, 2010: 1463-1469.

[8] T. Wan, Zengchang Qin. An application of compressive sensing for image fusion[C]//(2010), 2010: 3-9.

[9] X. Li, S. Y. Qin. Efficient fusion for infrared and visible images based on compressive sensing principle[J]., 2011, 5(2): 141-147.

[10] Xiaoyan Luo, Jun Zhang, Jingyu Yang, et al. Image fusion in compressed sensing[C]//(’07), 2009: 2205-2208.

[11] Schmidt M, Fung G, Rosales R. Fast optimization methods for Llregularization[C]//(), 2007: 286-297.

[12] Wang Z. B, Ma Y. D. Medical image fusion using m-PCNN[J]., 2008, 9(2): 176-185.

[13] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]., 2007, 53(12): 4655-4666.

[14] Haupt J., Nowak R. Signal reconstruction from noisy random projections[J]., 2006, 52(9): 4036-4048.

[15] E Candes. The restricted isometry property and its implications for compressed sensing[C]//, 2008: 589-592.

[16] Candes E , Romberg J，Tao T. Robust uncertainty principles; exact signal reconstruction from highly incomplete frequency information[J]., 2006, 52(2): 489-509.

[17] Xydeas C, Petrovic V. Objective image fusion performance measure[J]., 2000, 36(4): 308-309.

[18] Yang Senlin, GaoJinghuai. Seismicquality factors estimation from spectral correlation[J]., 2008, 5(4): 740-744.

An Image Fusion Algorithm Based on DCT Sparse Representation and Dual-PCNN

SONG Bin，WU Le-hua，TANG Xiao-jie，WEN Yu-qiang，MOU Yu-fei

(,400035,)

The existing image fusion method results in uneven image brightness, not agreeing with the original image contrast, not suitable for the human eye visual defects. To solve this problem, a new algorithm based on compressive sensing, which combined the DCT sparse representation with the Dual-channel pulse coupled neural network mode, is offered in this paper. First, for the character of the DCT sparse representation, Radial Sampling Matrix is designed. Second, the measurements based on the weighted average is fused with the information entropy of measurements. Finally, the total variation algorithm is used tore construct the fusion image. Experiments have been done to fuse multiple sets of different types of sensor image. Both subjective visual analysis and objective evaluation criteria show that the proposed algorithm can obtain more useful information from the original image, keep the edge information of original image, and get a better visual effect.

compressive sensing，dual-channel pulse coupled neural network，information entropy，the total variation algorithm

TP391

A

1001-8891(2015)04-0283-06

2014-12-23；

2015-02-05.

宋斌（1984-），男，湖北通山人，硕士研究生，主要研究方向为图像处理。

重庆市基础与前沿研究计划项目，编号：cstc2013jcyjA40045）；重庆市高校创新团队建设计划项目，编号：KJTD201343。