石英挠性加速度计数字闭环控制研究

朱海燕，叶凌云，彭皓岚，马才伟

(浙江大学 生物医学工程与仪器科学学院，浙江 杭州310027)

0 引 言

石英挠性加速度计数字闭环控制可以减小模拟闭环控制中因为A/D 转换导致的精度降低的问题［1］，并且易于控制和集成。关于石英挠性加速度计的数字闭环控制，多采用PWM 波反馈加矩的方式［2］。但是，由于加表表头的力矩线圈存在电感，因而会影响输入加速度值的准确测量。

针对该问题，国内外学者提出了基于A/D，D/A 直接转换驱动的方法［3，4］。该方法的反馈电流是直流信号，因而消除了线圈电感的影响。在数字闭环控制系统中，还需要一个合适的算法。国外Rojo D 等人提出过基于PID 算法的数字闭环加速度计设计专利［5］，国内北京航空航天大学等单位采用的也是PID 或PI 控制算法［3，6］。但是，该算法控制精度和实时性较差［7］。为了提高数字加速度计的性能，要求系统超调不超过5%，控制精度达到0.001%，调节时间在10 拍以内。

基于以上要求，本文提出了最少拍无纹波算法。该算法是一种时间最优的算法，理论上可以解决PID 算法的上述问题。本文针对具体的表头模型，分别设计出对应的PID 控制算法和最少拍无纹波控制算法，并仿真对比了系统超调、调节时间和稳态误差等性能指标。

1 数字闭环石英挠性加速度计表头模型

石英挠性加速度计表头相当于系统的传感器，其简化结构如图1 所示［8］。

摆片的动力学模型可以近似为典型的二阶模型［9］，数学方程式为

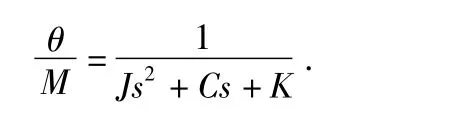
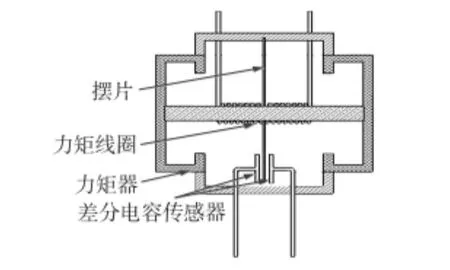
图1 石英挠性加速度计表头结构Fig 1 Mechanical meter structure of quartz flexible accelerometer

其中，θ 为摆片转角，(°);M 为外力矩，Nm;J为转动惯量，Nms2;C 为阻尼系数，Nms;K 为摆组件的刚度，Nm/rad。

这里不去详细讨论如何对表头进行数学模型的建立，而是以现有的石英挠性加速度计为研究对象来比较两种控制算法，其表头连续域传递函数［2］为

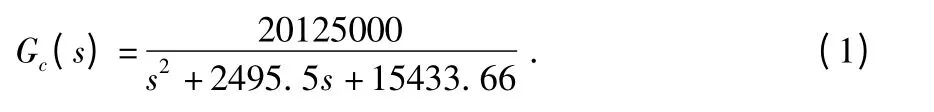
2 数字闭环加速度计最少拍无纹波控制算法设计

为了设计最少拍算法，首先需要知道最少拍系统的原理框图，如图2 所示。其中，R(z)为输入信号传递函数，D(z)为需要设计的数字控制器，G(z)为包含零阶保持器在内的广义受控对象传递函数，C(z)为输出信号传递函数，Φ(z)为闭环系统传递函数。

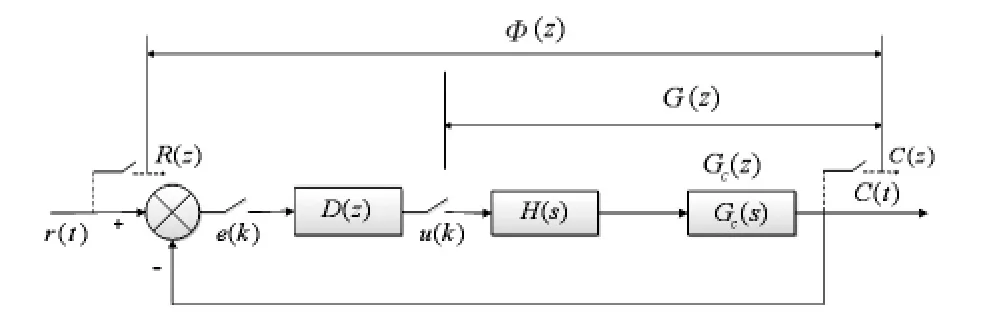
图2 最少拍控制系统原理框图Fig 2 Principle block diagram of deadbeat control

由图2 可以得出系统的闭环Z 域传递函数为

其中

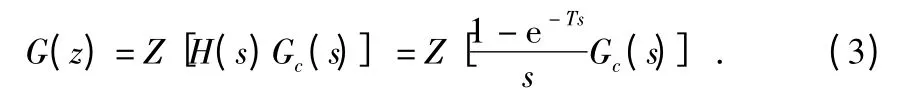
可见，求解最少拍无纹波控制器的步骤有以下三步:

1)构建被控对象的数学模型，即求解Gc(s);

2)确定系统采样频率，即确定H(s)的表达式;

3)根据系统最少拍无纹波的要求，构造Φ(z)。

步骤(1)在上面已有说明，这里不再赘述，下面介绍步骤(2)，(3)。

2.1 采样频率的确定

理论上采样频率越高，越能复现原始信号。但是，采样率增加会使系统带宽增大，引入更多的高频噪声［10］。另外，采样率增加会使系统的极点更趋近单位圆，降低了系统的稳定性。所以，采样率的确定要综合各种因素来考虑。根据经验，一般设定采样率为系统带宽的10 ～20 倍，这样可以确保数字控制器与连续控制器的性能相匹配［11］。由于加速度信号的频率一般不会超过1 kHz，所以，本文最终选取采样频率为10 kHz。

2.2 最少拍无纹波控制器设计

由上面式(1)、式(3)可得

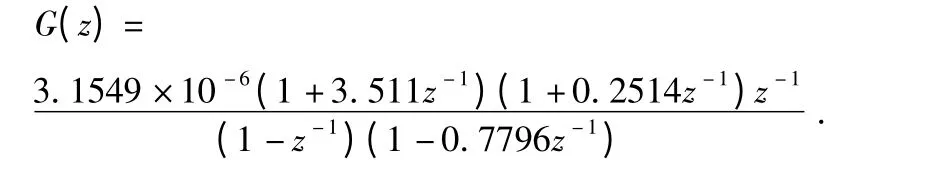
由图2 可知，控制系统的误差信号e(k)的Z 域传递函数为

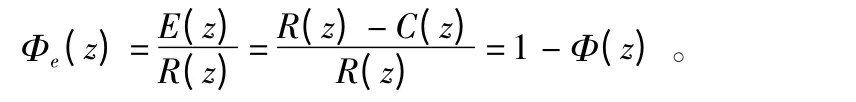
误差传递函数Φe(z)会因为不同的典型输入信号而不同，本系统的输入信号可以认为是一个个小的阶跃信号［12］。单位阶跃信号的Z 变换为

根据系统稳定性的要求可得

最终得到数字控制器传递函数为

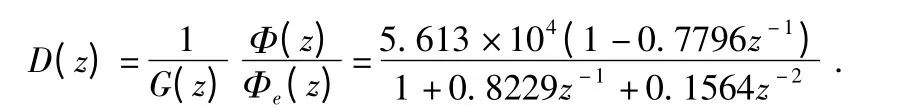
3 仿真验证

本文对两种算法的控制效果进行了Simulink 仿真，在相同的采样频率和系统带宽的条件下，对比了系统超调、调节时间和稳态误差等方面性能。

3.1 最少拍无纹波控制算法的Simulink 仿真

Simulink 环境下的最少拍无纹波控制算法仿真框图如图3 所示，输入是单位阶跃信号(Step)，输出通过示波器(Scope)来观察，采样频率f=10 kHz。

图3 最少拍无纹波控制算法Simulink 仿真图Fig 3 Simulation diagram of ripple-free deadbeat control algorithm by simulink

仿真结果如图4(a)～(d)所示。

由图4 可以得到系统具体性能指标如表1 所示。

表1 最少拍无纹波控制系统性能指标Tab 1 Performance indexes of ripple-free deadbeat control system

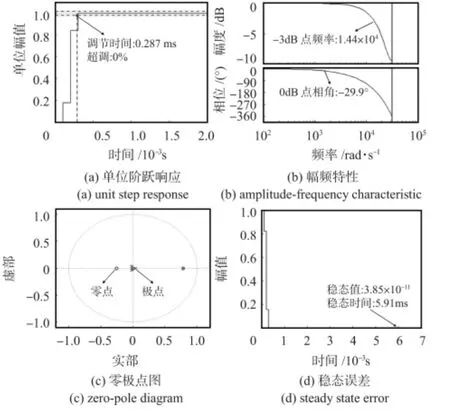
图4 最少拍无纹波控制算法仿真结果Fig 4 Simulation results of ripple-free deadbeat control algorithm

3.2 PID 控制算法的Simulink 仿真

Simulink 环境下的PID 控制算法仿真框图如图5 所示。

图5 PID 算法的Simulink 仿真图Fig 5 Simulation diagram of PID algorithm by simulink

通过调节Simulink 工具箱中的Tune 按钮，动态地调整PID 参数，使得系统的带宽与最少拍无纹波控制算法一致。仿真结果如图6(a)～(d)所示。

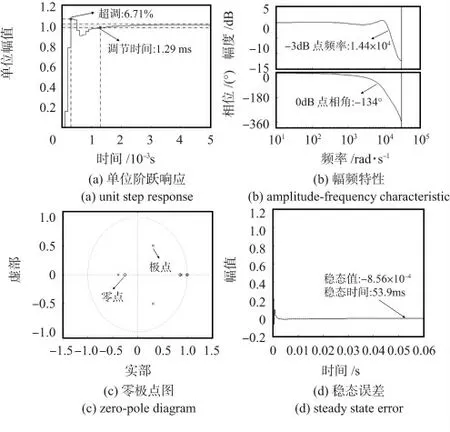
图6 PID 控制算法仿真结果Fig 6 Simulation results of PID control algorithm

由图6 可以得到系统具体性能指标如表2 所示。

表2 PID 控制系统性能指标Tab 2 Performance indexes of PID control system

结合图4(a)和图6(a)可知，PID 控制系统超调为6.71%，超过5%，远大于最少拍算法的超调;调节时间为1.29 ms，超过10 拍，远大于最少拍算法的0.287 ms。因此，PID 控制系统的实时性和相对稳定性较最少拍算法要差。

结合图4(b)和图6(b)可知，PID 控制系统的谐振峰增益相对较大，幅值裕度和相位裕度相对较小，系统的稳定性较最少拍算法要差。

结合图4(c)和图6(c)可知，PID 控制系统的极点分布更趋向于单位圆，系统的相对稳定性较最少拍算法要差。

结合图4(d)和图6(d)可知，PID 控制系统的稳态误差为8.56×10－4，大于0.001%，而最少拍系统的稳态误差只有3.85×10－11，远小于0.001%。PID 控制系统达到该精度的时间为53.9 ms，远大于最少拍系统的5.9 ms。因此，PID 系统的控制精度和响应速度较最少拍算法要差。

综合以上可知，虽然PID 算法可以使系统稳定，但是与最少拍无纹波控制算法相比，PID 算法达到稳态需要更长的调节间，并且系统的超调和稳态误差也更大。因此，PID控制算法在系统实时性、准确性、稳定性等方面的性能较最少拍无纹波算法相对较差。

4 结 论

在石英挠性加速度计数字闭环控制系统中，最少拍无纹波算法比PID 算法具有更好的控制性能。仿真证明:在相同的带宽和采样频率下，最少拍无纹波算法的超调量远小于5%，调节时间只需要3 个采样周期，稳态精度可以达到0.001%以下，综合性能优于PID 算法。因此，在一些对控制精度和响应速度均有较高要求的场合，最少拍无纹波控制算法有着很大的应用价值。

［1］ Li Lin，Zhang Chunxi，Zhang Xi，et al.Investigation on noise of digital closed-loop Q-flex accelerometer［C］∥6th IEEE Int'l Conference on Industrial Electronics and Applications(ICIEA)，Beijing:IEEE，2011:614－619.

［2］ 夏 瑜.石英挠性摆式加速度计全数字伺服回路技术［D］.天津:河北工业大学，2008:14－19.

［3］ 张 晞，张声艳，顾欣怡，等.数字闭环石英挠性加速度计表头离散化研究［J］.传感器与微系统，2012，31(12):62－65.

［4］ Soen Jonathan，Voda Alina，Condemine Cyril.Controller design for a closed-loop micromachined accelerometer［J］.Control Engineering Practice，2007，15(1):57－68.

［5］ Rojo D.Closed-loop accelerometer system，has rebalancing controller comprising proportional-integral-derivative control portion having variable gain components，where controller is in signal communication with driver:US，2010057224—A1［P］.2010—03—04.

［6］ 顾欣怡，张 晞，魏 渊.数字闭环加速度计控制器设计与仿真［J］.弹箭与制导学报，2012，32(6):170－173.

［7］ 曹承志.微型计算机控制新技术［M］.北京:机械工业出版社，2001:170.

［8］ 陈 浩.基于ARM 的石英挠性加速度计采集处理系统设计［D］.哈尔滨:哈尔滨工程大学，2007:4－5.

［9］ 毛伟玲.基于模型辨识的石英挠性加速度计控制回路设计［D］.天津:天津大学，2012:21－23.

［10］张 晞，张声艳，曹巧媛.数字闭环石英挠性加速度计量化误差分析与实验研究［J］.传感器与微系统，2013，32(11):33－36.

［11］Franklin G F，Powell J D，Emami-Naeini A.Feedback control of dynamic systems［M］.Beijing:Publishing House of Electronics Industry，2004:442－443.

［12］叶凌云，陈 波，张 建，等.基于最少拍无纹波算法的高精度动态标准源反馈控制［J］.浙江大学学报:工学版，2013，47(9):1554－1558.