面向无线传感器网络的无线携能通信研究*

王世强，邢建春，李决龙，杨启亮，3

(1.解放军理工大学 国防工程学院，江苏 南京210007;2.海军海防工程研究中心，北京100841;3.计算机软件新技术国家重点实验室(南京大学)，江苏 南京210093)

0 引 言

无线传感器网络(wireless sensor networks，WSNs)将逻辑上的信息世界与真实的物理世界融合在一起，可广泛地应用于军事、国防工程、工农业控制等诸多领域。然而，无线传感器节点一般采用电池供电，电池的周期性更换将大大增加网络维护成本，并且，很多传感器网络(如结构健康监测传感器网络)因为需要长时间工作在特殊环境下，替换电池是不可能的。

无线携能通信(simultaneous wireless information and power transfer，SWIPT)技术将发射出的同一电磁波不仅用于信息传输，还用于能量获取，能够为能量受限型网络提供持久的能量供应，近年迅速成为研究热点［1］。

Varshney L R 在假设接收电路能够同时从接收信号中进行信息解调和能量获取的条件下，首次提出信息和能量同时传输的思想［2］。然而，这样的假设在实际中是不成立的。因为目前的硬件电路无法在解调信息的同时，收集作为载体的无线电波所携带的能量。在传统无线通信中，无线电波所携带的能量最终都以热能的形式耗散。从上述问题出发，文献［3，4］提出了动态功率分配(dynamic power splitting，DPS)方式作为无线携能通信技术的解决方案。基于DPS 方式，文献［5 ～8］研究了无线携能通信在多用户系统中的应用。Fouladgar A M 在文献［9］中提出了一种受约束的RLL(run length limited)编码规则，使系统更适合信息与能量的权衡。文献［10］将无线携能通信应用于认知无线电中，最大化次用户的可获得吞吐量。文献［11］详细分析了无线携能通信在正交频分复用(OFDM)系统中的应用。

然而，现有工作中的无线携能通信系统存在两点不足:第一，优化模型只注重效率性，却忽视了公平性;第二，在满足最低能耗时，如果一味地提高信息速率，对于信息速率要求不高的场合只会造成能量的浪费。

本文将无线携能通信技术应用在无线传感器网络中，针对现有优化模型存在的不足，建立了适应于无线传感器网络的新优化模型。基于时分多址(time division multiple address，TDMA)机制，与TS 方式相结合，研究了无线传感器网络的无线携能通信系统。

1 系统描述

无线携能通信主要应用在无线传感器网络中信息量比较小的下行链路中，如图1 所示。

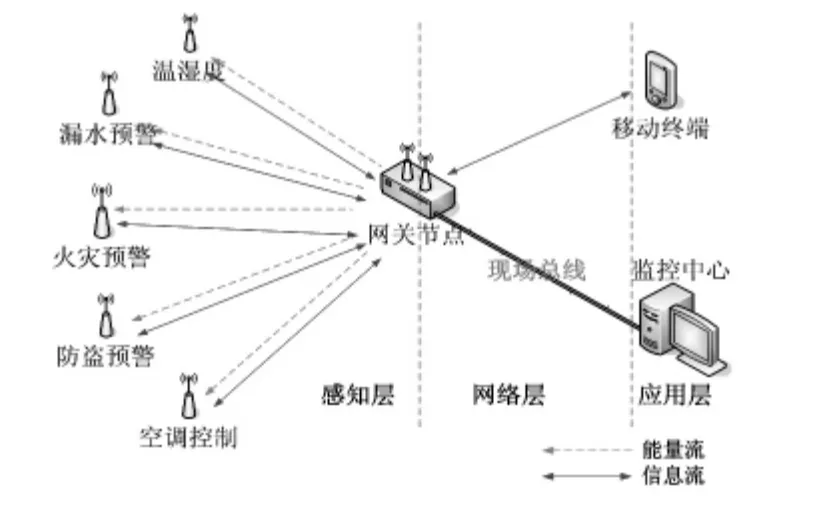
图1 无线传感器网络信息与能量传输Fig 1 Information and energy transmission of wireless sensor networks

建立具有K 个传感器节点的无线携能通信系统。设定最大发射功率为P，第k 个时隙的发射功率为pk，规定每个时隙的峰值发射功率为ppeak，则0≤pk≤ppeak;第k 个传感节点的信道增益为hk;选用高斯白噪声作为信道中的噪声模型，且均值为0，方差为σ2;Γ 为SNR 距离。

传感节点硬件电路中既有信号解调模块，又有能量收集模块，二者通过转换开关进行切换，如图2 所示。

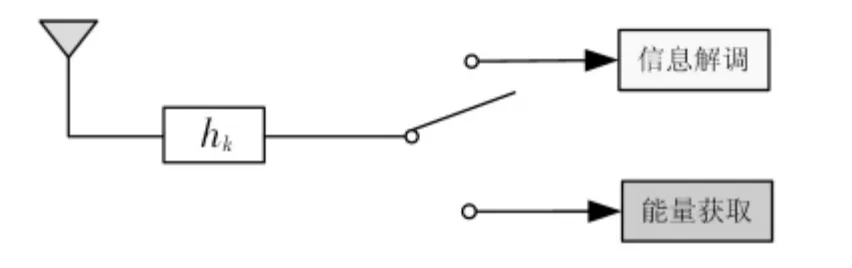
图2 TS 方式的无线携能通信Fig 2 Simultaneous wireless information and power transfer by TS mode

采用TS 方式设计基于TDMA 的无线携能通信系统。指定时隙k(k=1，…，K)用于传感节点k 的信息传输。为简单起见，将总传输时间进行归一化处理。每个时隙的持续时间是动态变化的，时隙k(k=1，…，K)的持续时间用αk表示，则0≤αk≤1。因此，最大传输功率可表示为

传感节点k 在第k 个时隙进行信号解调，在其余时隙进行能量获取，如图3 所示。

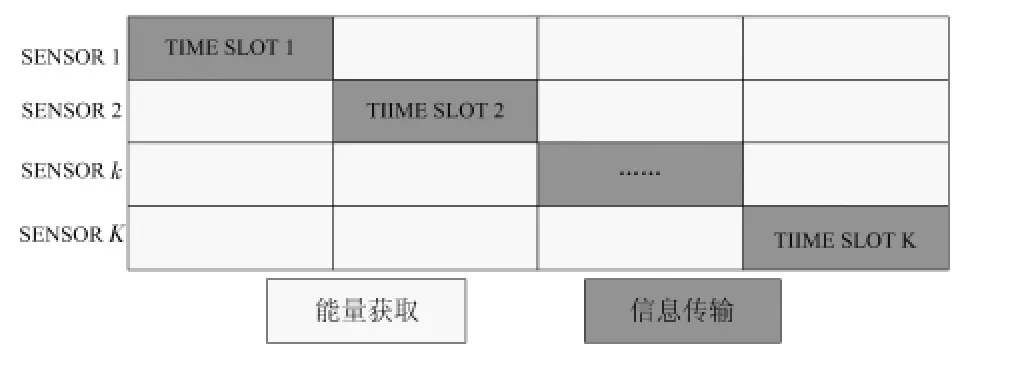
图3 基于TDMA 的无线携能通信Fig 3 Simultaneous wireless information and power transfer based on TDMA

传感节点k 的信息传输速率(单位:bps/Hz)可表示为

设定传感节点的能量转换效率为ζ(0 ＜ζ ＜1)，则传感节点k 的能量获取(单位:μW)可表示为

2 系统模型建立

无线携能通信系统的优化目标主要有:通过调整每个时隙的功率和时间分配，最大化信息传输速率和能量获取量。以往工作是将能量获取目标作为约束条件构建优化模型，使信息传输速率最大化。

本文采用线性加权的方法建立目标函数。为了保证公平性，防止信道状态较好的节点消耗过多的信道资源，满足不同节点对能量和流量消耗的不同需求。设定每个节点的最小速率和最低能量需求为和

因此，构建如下的优化模型

其中，ψ 为加权因子，反映了通信过程中是偏向能量获取，还是信息传输。

3 最优化资源分配策略

无线携能通信中能量作为重要资源，与频谱等共同参与分配，进而需要构建新的分配策略。

现有形式的式(4)为非凸优化问题，通过引入非负变量:qk=αkрk(k=1，…，K)，并且为了保证连续性，当αk=0时，定义

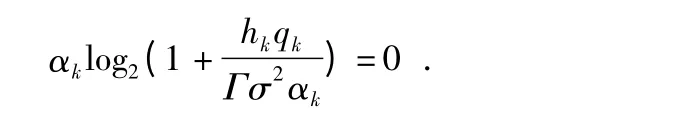
式(4)可以转换为

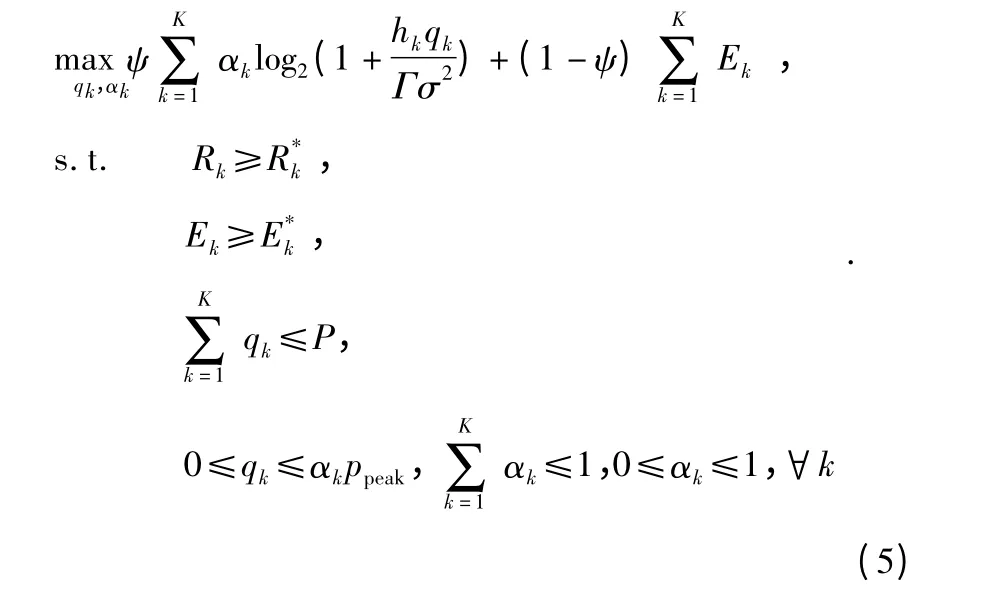
当qk≥0，αk≥0 时，f(qk，αk)为凸函数，其中

从而得到拉格朗日函数

其中，λi(i=1，…，K)，θk(k=1，…，K)，u，v 为对应于各约束条件的非负对偶变量，进而原始问题的对偶函数g({λi}，{θk}，u，v)可以转换为

令

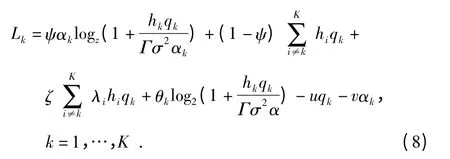
求最小值

从而拉格朗日函数的变形为

最优化问题可被分解为针对K 个时隙的子问题

Lk对qk(k=1，…，K)求偏导得

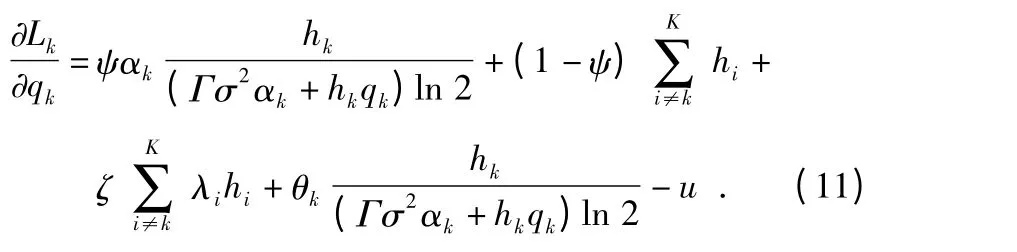
当αk给定时，令

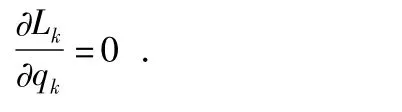
可得使Lk取最大值的

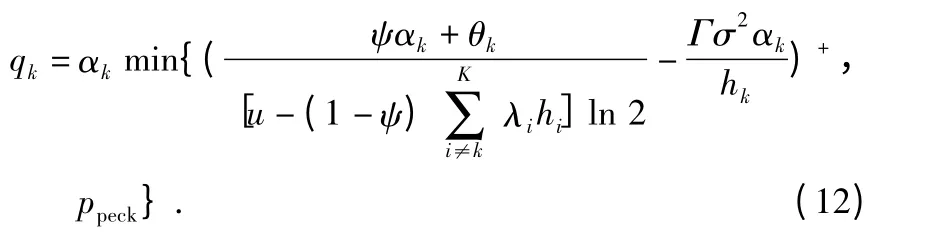
其中，(x)+=max(0，x)。

Lk无法对αk求出解析解，故可以利用数值解法求得在一定误差范围内的。

最后，采用次梯度迭代的方法求解g({λi}，{θk}，u，v)的{λi}，{θk}，u，v 的最优值，各变量的次梯度如式(13)

求解算法总结如下:

初始化对偶变量{λi}，{θk}，u，v;

循环

1)初始化αk=1/K，k=1，…K;

2)循环

a)通过式(14)计算{qk}，k=1，…，K;

b)通过牛顿迭代法计算使Lk({qk}固定)的取最大值的αk，k=1，…K;

3)直到Lk达到指定精度要求;

4)计算g({λi}，{θk}，u，v)的次梯度;

5)利用次梯度迭代的方法对{λi}，{θk}，u，v 更新;

直到{λi}，{θk}，u，v 达到指定的精度要求;

4 仿真结果分析

结合工程需求，为简单起见，这里以具有三个节点的传感器网络为例，对以上结果进行仿真。

根据国际非电离无线电保护委员会(International Commission for Non-Ionizing Radiation Protection，ICNIRP)制定的电磁辐射安全限度标准，在满足卫生要求的前提下，有效全向发射功率(effective isotropic radiated power，EIRP)控制在10 W 以下。

设置参数如下:

噪声功率σ2=10 μW/Hz(或－20 dBm/Hz)，信道增益h1=－17 dB，h2=h3=－20 dB，即传感器1 的信道状况要比传感器2 和传感器3 差。能量转换效率ζ=0.2，SNR 距离Γ=1。工程中温湿度传感器的能耗一般设置在μW 级。

利用表1 的求解算法，得到仿真结果如图4、图5。

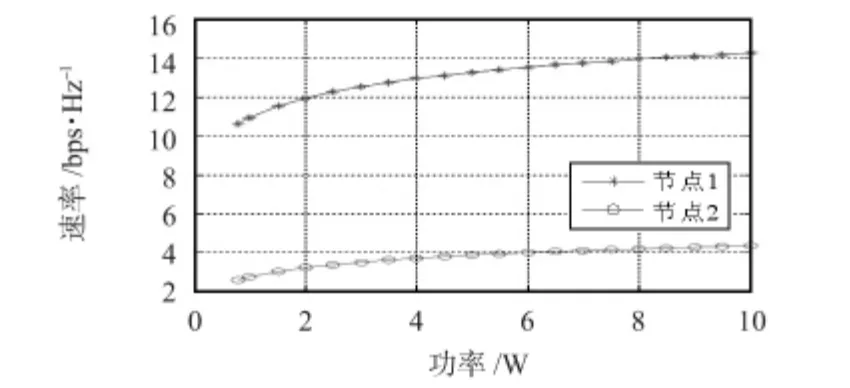
图4 原优化模型下节点速率Fig 4 Node rate under the original optimization model

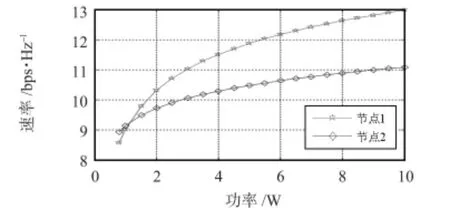
图5 新优化模型下节点速率Fig 5 Node rate under the improved optimization model

图4 和图5 分别为原优化模型和新优化模型节点的速率随发射功率的变化情况，其中新优化模型约束条件=，由于节点2 和节点3 的信道状况和需求设定为一致，故图中仅对差异比较大的节点1 和节点2 进行对比，便可说明问题;图6 为两种模型的总容量对比。

虽然原优化模型总容量要比新优化模型大(如图6)，但是原优化模型中由于节点2 的信道增益比较差，使得节点2 的速率很低(小于4.5 bps/Hz)，即使发射功率增大，节点2 速率增加不明显，而节点1 的速率一直很高(如图4)，这可能导致节点2 的速率达不到节点通信需求。新优化模型中对节点2 的速率给定最低值，速率得以提升(如图5)，达到系统需求。

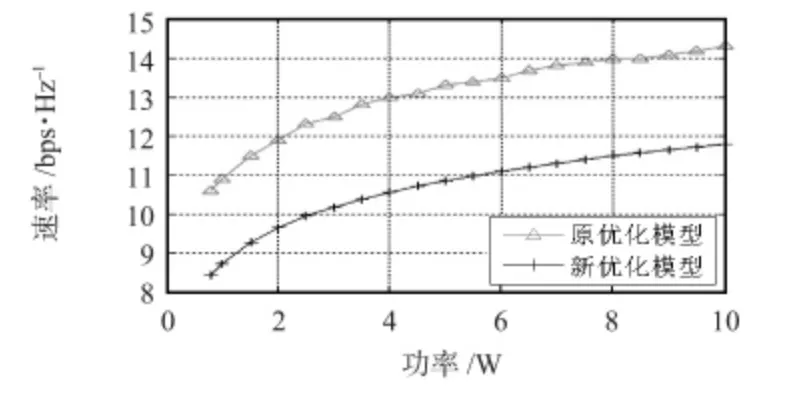
图6 总容量对比Fig 6 Comparison of total capacity

图7 为两种不同优化模型获取总能量的对比，其中新优化模型中加权因子ψ 取特殊值0，即偏向于能量获取，原优化模型约束条件与新优化模型一致。由仿真结果可得，新优化模型获取的能量要比原优化模型提高将近20%，更加适合于能量受限型网络。实际系统中，可以根据对能量和速率的需求调整ψ 的取值进行调整。

图7 总能量对比Fig 7 Comparison of total energy

5 结 论

本文构建了基于TDMA 的无线携能通信系统，针对无线传感器网络自身的特点，建立了新的优化模型。实验结果表明:该模型更加注重公平性，更加适应网络的多样性需求，并使获取能量最大化。将无线携能通信应用在无线传感器网络是合理的，能够为无线传感器网络的能量问题提供新的解决方案。

［1］ Huang K B，Larsson E.Simultaneous information and power transfer for broadband wireless systems［J］.IEEE Transactions on Signal Processing，2013，61(23):674－681.

［2］ Varshney L R.Transporting information and energy simultaneously［C］∥Proc IEEE Int’l Symposium on Information Theory(ISIT)，2008:1612－1616.

［3］ Zhang R，Ho C K.MIMO broadcasting for simultaneous wireless information and power transfer［J］.IEEE Transactions on Wireless Communications，2013，12(5):1989－2001.

［4］ Zhou X，Zhang R，Ho C K.Wireless information and power transfer:Architecture design and rate-energy tradeoff［J］.IEEE Transactions on Communications，2013，61(11):4754－4767.

［5］ Xu J，Liu L，Zhang R.Multiuser MISO beamforming for simultaneous wireless information and power transfer［C］∥Proc of IEEE International Conference on Acoustics，Speech，and Signal Processing(ICASSP)，Vancouver，Canada:IEEE，2013:4754－4758.

［6］ Liu L，Zhang R，Chua K C.Wireless information transfer with opportunistic energy harvesting［J］.IEEE Transactions on Wireless Communications，2013，12(1):288－300.

［7］ Liu L，Zhang R，Chua K C.Wireless information and power transfer:A dynamic power splitting approach［J］.IEEE Transactions on Communications，2013，61(9):3990－4001.

［8］ Park J，Clerckx B.Joint wireless information and energy transfer in a two-user MIMO interference channel［J］.IEEE Transactions on Wireless Communications，2013，12(8):4210－4221.

［9］ Fouladgar A M，Simeone O.Constrained codes for joint energy and information transfer［J］.IEEE Transactions on Communications，2014，62(6):1251－1260.

［10］Zheng G，Ho Z，Jorswieck E A.Information and energy cooperation in cognitive radio networks［J］.IEEE Transactions on Signal Processing，2014，62(9):2031－2038.

［11］Ng D W，Lo E S，Schober R.Wireless information and power transfer:Energy efficiency optimization in OFDMA systems［J］.IEEE Transactions on Wireless Communications，2013，12(12):1536－1276.