保险公司的最优投资比例研究

雷丹， 王源昌， 张芬

(云南师范大学 数学学院，云南 昆明 650500)

1 问题的提出

随着我国改革的不断深化和经济市场化程度的提高,我国保险公司之间的竞争也越来越激烈.很多保险公司都通过降低保费来扩大公司的市场占有率,造成有些保险公司收取的保费越来越低，出现亏损.这样一来,合理地利用保险资金进行投资,获得利润,对保险公司的生存和发展都至关重要.保险公司应该在有效控制风险的前提下,选择最优的投资方案,尽可能地提高投资收益率[1].

传统的最优投资问题分析为简化计算,都假定无风险利率是确定的.但事实上，利率会不断调整,具有随机性.对利率随机性的研究在近年来逐步受到重视,人们开始注意到由利率随机性产生的风险是相当大的[2].

本文分别在常利率模型和随机利率模型下,利用随机最优控制的动态规划方法,对保险公司的最优投资比例进行求解.对两种模型得出的结果进行比较,表明了考虑随机利率的必要性.这对保险公司更加合理的运用保险资金进行投资有重要的理论和实际意义.

2 模型构建与求解

2.1 动态规划方法简介

设(t,x)∈[0,T]×Rn,考虑下面的状态方程

成本函数为

定义它的值函数为

其中X(·)是初始值条件为X(t)=x，与控制u(·)一致的状态过程.

命题2.1.2 如果V(·,·)、Vt(·,·)、Vx(·,·)、Vxx(·,·)都是连续的，则V(·,·)满足下面的Hamilton-Jacobi-Bellman方程

2.2 模型的建立

设N是一个参数为λ的泊松过程，Yi>0,i=1,2,…是独立同分布序列，取值为非负，且{Yi}与N相互独立.c>0，令

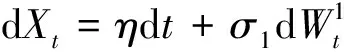
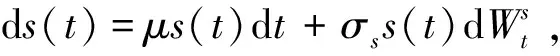
模型假设：

(1)用于投保的初始资金X0=x;

(2)投资于风险资产的资金比例是由公司自己决定的;

(3)公司的决策总是为了实现终端财富的期望效用最大化;

(4)没有交易费用;

(5)风险资产的收益率高于无风险资产的收益率.

公司的总资产变化满足如下随机微分方程[4]

2.3 常利率模型下求解保险公司的最优投资问题

最大化终端财富的期望效用函数为目标：设T是终端时刻，效用函数为U(x)，值函数

首先给出该问题的HJB方程

(1)

解得

代入方程(1)中，整理可得

(2)

设保险公司追求期末财富效用最大化，在这个过程中，资金的安全性非常重要.所以在效用函数是常系数绝对风险厌恶的情况下讨论.

其中g(·)是一个待定的函数，由边值条件有g(0)=0.在这种情况下易得

代入方程(2)中，整理可知g(·)需要满足如下方程

积分并令g(0)=0，则有

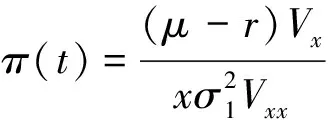
(3)

2.4 随机利率下求解保险公司的最优投资问题

公司的总资产变化满足如下随机微分方程

式中v为初始盈余.

Vasicek随机利率模型为

最大化终端财富的期望效用函数为目标：设T是终端时刻，效用函数为U(x)，值函数

首先给出该问题的HJB方程

(4)

其中

对其求最大值，将上式对π求导，并令其等于零可得

解得

代入方程(4)中，整理可得

(5)

其中g(·)是一个待定的函数，由边值条件有g(0)=0.在这种情况下易得

代入方程(5)中，整理可知g(T-t)需要满足如下方程

积分并令g(0)=0，则有

(6)

其中λ=1+r(T-t).

3 实证分析

本论文在建立模型时,假设风险资产的收益率是比无风险资产的收益率高的.但是由于全球经济危机的影响,从2007年开始,投资于风险资产的收益率普遍下降,低于存款利率,有时还是负值.所以在对本模型的实证研究中,采取2005年全年以及2006年上半年的数据.

3.1 无风险利率的确定[6]

我国以银行存款利率作为金融资产定价的基准,所以采用银行存款利率作为无风险利率.本文采用一年期的定期存款利率作为无风险资产,那么,利率的平均值就可以作为无风险资产的收益率.本文收集了从1990年1月至2012年7月的中国人民银行公布的一年期定期存款利率,计算得平均值为rf=4.27%,波动率为σf=0.007 89.

3.2 风险资产的确定

选取上证国债指数、上证企债指数、上证180指数和上证基金指数作为风险资产.选取从2005年1月至2006年6月之间的收盘数据作为研究样本,计算其年平均收益率作为风险资产的收益率.计算其方差,作为风险资产的波动率.计算结果见表1.

表1 四种风险资产的年平均收益率及波动率

对四种风险资产的平均收益率和波动率取平均值,来作为投资于风险资产的平均收益率和波动率.计算得μ=20.46%,σs=4.97%.

在计算风险资产与无风险资产之间的相关系数时,采用的是1992年1月至2012年7月的数据,计算得ρ=-0.31.

3.3 实证研究

采用中国人寿保险公司的投资情况来做实证研究.在2005年全年和2006年上半年中，中国人寿保险公司可用来进行投资的资金平均为55 921 900万元.风险偏好系数为0.5.

将以上计算所得的数据代入(3)式和(6)式中，计算得，在不考虑利率的随机性的情况下，投资于风险资产的比例为0.000 306%.在考虑了利率随机性的情况下，投资于风险资产的比例为5.45%.而在实际情况中,中国人寿保险公司投资于风险资产的比例为4.2%(本数据来源于中国人寿2005年报和2006中报).显然,在考虑了利率随机性的情况下,计算所得的比例更接近实际情况.

4 结束语

保险公司的最优投资比例问题是近年来学术界关注的一个问题，但是现有的研究很少考虑到利率的随机性.本文在考虑随机利率的情况下,建立了HJB方程.同时，因为保险公司在投资时，最重要的是保证资金的安全性，所以采用指数效用函数作为保险公司的效用函数，解出了最优投资比例.

最后将求解的结果运用到实际中，采用中国人寿保险公司的数据进行实证.结果显示，考虑了利率的随机性的模型,计算出的结果更加符合实际，也就更加的现实指导意义.

[1] BROWNE S.Optimal investment policies for a firm with a random risk process exponential utility and minimizing the probability of ruin[J].Mathematics of Operations Research,1995,20(4):937-958.

[2] TAKSAR M,MARKUSEEN C.Optimal dynamic reinsurance policies for large insurance portfolios[J].Finance Stochastics,2003(7):97-121.

[3] 郭文旌.保险公司的最优投资策略选择[J].数理统计与管理,2010,29(1):144-149.

[4] 袁远,施齐焉.基于Hamilton-Jacobi-Bellman方程求解保险业最优投资策略[J].经济数学,2012,29(4):105-110.

[5] 荣喜民,范立鑫.常弹性方差保险模型下保险人的最优投资策略[J].系统工程理论与实践，2012，32(12),2619-2628.

[6] 张景肖.随机最优控制及其在保险中的应用[M].北京：科学出版社，2013.