地面控制点对机载LiDAR航带平差结果影响分析
2015-03-30孙秉钊
陈 洁,杜 磊,李 京,孙秉钊
(1.中国国土资源航空物探遥感中心,北京100083;2.中国科学院遥感与数字地球研究所,北京100101)
集成了全球定位系统(Global Positioning System,GPS)和惯性测量单元(inertial measurement unit,IMU)的机载LiDAR技术,利用GPS得到航空遥感平台的精确三维位置和IMU测得的空中姿态信息,结合激光测距仪精确测定与地面点的距离,根据几何原理就可以计算出激光点的三维位置,从而使其具备了采集高精度三维地形数据的能力[1]。由于硬件方面的限制,机载LiDAR具有一定的扫描宽度,在进行大面积数据采集时,需进行多条航带的扫描,各航带间的重叠度约为15%~20%。在航带重叠区域内的同名地物点,因为机载LiDAR系统间安置角误差产生的系统误差会引起航带间的相对位置偏差。为了改正此偏差,通常采用两种方式:一是直接进行检校场飞行,二是利用共轭方程进行航带平差[2]。检校场飞行理论上需要每架次进行,且检校场的选择条件较为苛刻,并要进行地面测量工作[3],严重影响了机载LiDAR快速成图技术优势。为了提高作业效率,通常采用文献[4]提出的航带平差方法进行系统误差校正,以消除或减少航带间偏差。
文献[4]航带平差方程采用可能造成系统误差的物理变量为参数,利用地面已知控制点求解这些物理参数值,达到改正误差的目的。但方程中各参数间相关性较高,理论上所需的控制点数量较多,也在一定程度上增加了作业量和周期。为此,本文对是否采用地面控制点进行航带平差进行了实践应用,研究分析了控制点的引入对航带平差结果和整体点云精度的影响。
一、航带性系统误差改正
引起航带偏差的各种误差中,系统误差是其主要来源。各集成单元的仪器测量差、定标误差和解算误差等,可利用设备厂商提供的检校文件予以较好的修正。但由于各测量单元间的坐标系转换和安置角的不确定性引起的系统差,则需要对所采集的点云数据进行航带平差予以改正。
在进行航带平差时,需考虑以下4方面的问题:①选用适当的数学模型来描述航带间的变形参数,例如常使用的坐标系统间转换的七参数[5]、九参数[6]和十二参数[7]等,航带变形参数的选择必须与实际情况相吻合,否则平差效果可能不明显,还有可能造成因为使用参数过量而产生的其他误差;②根据最小二乘平差原理,选择最优的平差模型进行变形参数计算;③布设一定数量的地面控制点用来赋予点云数据具有精确的绝对坐标信息;④在航带重叠区域内进行连接点的匹配运算,通过连接点的平差来计算变形参数。
因此,本文使用的目前已相对较为成熟的文献[8]提出的航带平差原理和处理方法流程进行研究分析,采用的软件为TerraSolid商业软件系列中的TerraMatch模块。
1.航带平差方法原理
文献[8]的观测方程式如下
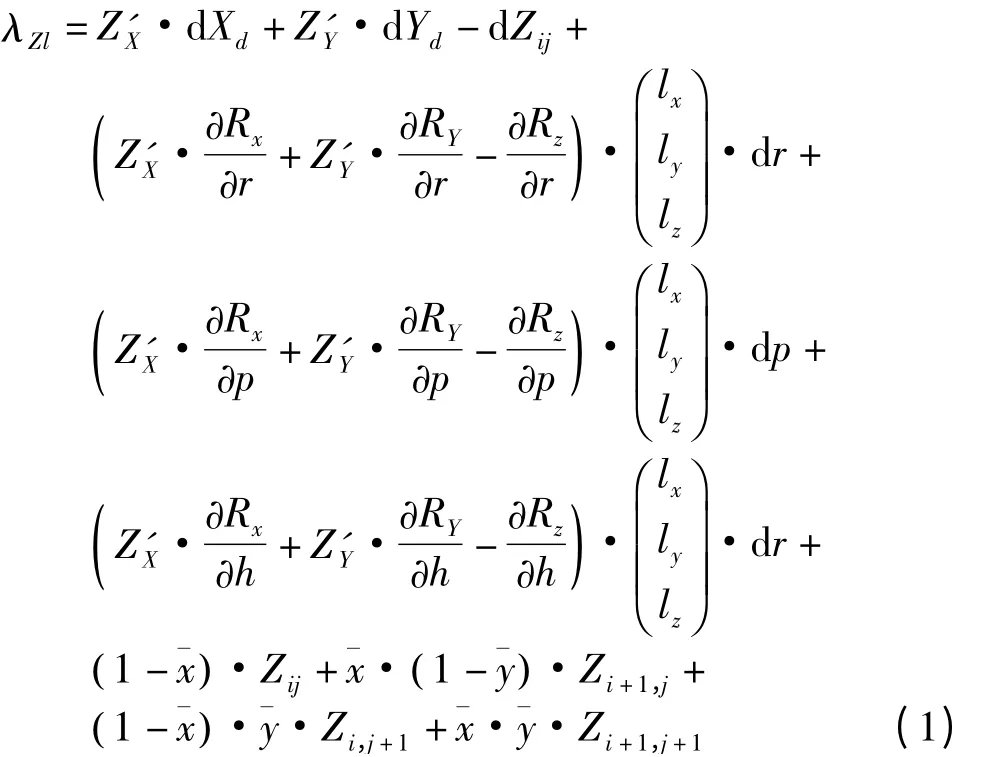
式中,λZl为观测高程值与格网内高程值的差值;(d Xd,d Yd,d Zd)为基准偏移变量;d Zij为高程格网点高程的改正值;r、p、h为3个安置角初始值;d r、d p、d h为安置角改正值;¯x、¯y为4个各网点的归一化坐标近似值。
最小二乘平差公式为
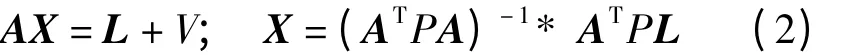
对每条航线而言,其主要未知参数有3个方向的平移量和漂移量,3个轴角偏移量与漂移量。利用最小二乘平差公式求解未知参数X,其中观测矩阵L由重叠区的地面点、房屋和地面控制点组成,P为各观测值权重。由于未知参数之间存在参数高相关,一方面可以通过加入地面控制点方法解决;另一方面可以减少参数量,如去除平移参数和线性漂移量的未知数,会有较稳健的解算结果。未知参数需要输入迭代收敛和标准差的先验条件。
2.航带平差处理流程
(1)数据和资料准备
工作区航带机载激光雷达数据、飞行轨迹文件、地面控制点资料。对于大面积机载激光雷达飞行作业,建议在测区内布设适量地面控制点,以避免出现航带平差结果相对精度提高而损失绝对精度的情况。地面控制点的布设原则是控制点需要分布均匀,同时对地形地貌复杂区需重点控制。
(2)各航带分别进行点云分类
由于激光点云中存在的一些噪声点和大量植被点会对航带间比较和平差处理造成干扰,需要逐条航带进行地面点和房屋分类。采用的方法是:地面点分类可利用软件自动进行,房屋点采用人工分类以提高分类精度,对于地面点中典型地区(如平地或光滑坡面)和房屋点,在航带平差参数解算时应给予较大的权重。
(3)参数解算
利用TerraMatch软件迭代计算各航线的参数修正量。解算方式分无地面控制点和含地面控制点两种,并一般只针对d z、d r、d p、d h为未知参数计算,其他漂移量在短航线测量可以忽略。根据已有资料对不同参数解算难易程度的分析,航带间高程方向和测滚(Roll)方向上的偏移量d z和d r的解算比较容易实现,在仅有平坦地面的情况下就可以进行(如图1所示);俯仰(Pitch)和方向性(Heading)偏移参数的解算则相对困难,Pitch需要有飞行方向的坡面,Heading则需同时有飞行和垂直飞行方向的坡面(如图2所示)。
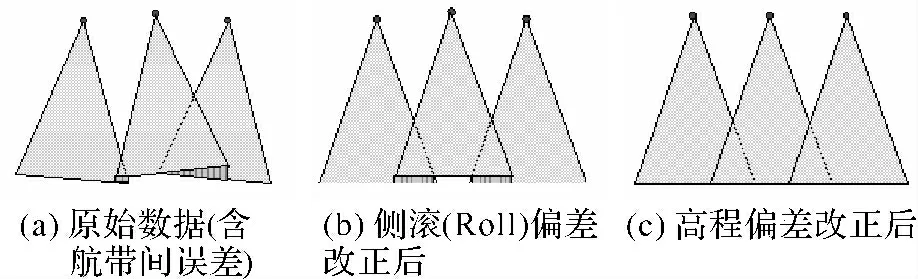
图1 侧滚和高程方向偏差改正示意图
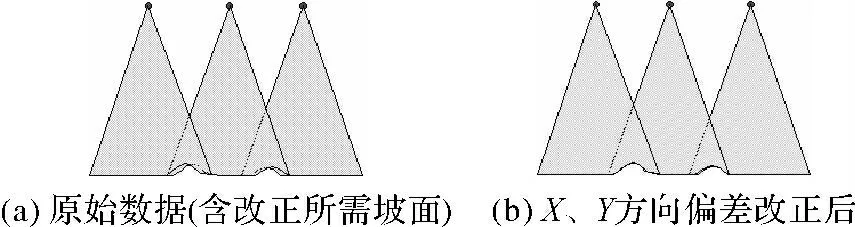
图2 俯仰和方向性偏差改正示意图
整个解算过程分为数据工程整体参数解算和各航线调整参数分别解算两个步骤。工程整体参数解算方法为:在工作区内尽量分布均匀地选择航线重叠区中含有平地、光滑坡面和房屋点等典型地物的区块,并利用这些区块创建工程文件。用Terra-Match软件对该工程文件进行飞行姿态偏移(hrp)和扫描镜尺度(mirror scale)误差参数解算,并将解算参数应用于全部测区数据的改正。各航线调整参数分别解算方法为:将全部测区数据组成区块性的工程文件,其中可以去除植被覆盖度过大造成无地面点或地面点稀少的区块,然后解算每一条航线的高程偏移d z(此时也可同时解算侧滚roll)改正参数。
根据解算出的参数修正量修正激光点云数据,并对平差后的成果数据精度改善情况进行分析评价,利用航线重叠区数据评价内部精度,用地面控制点检测数据的外部精度。
航带平差作业流程如图3所示。
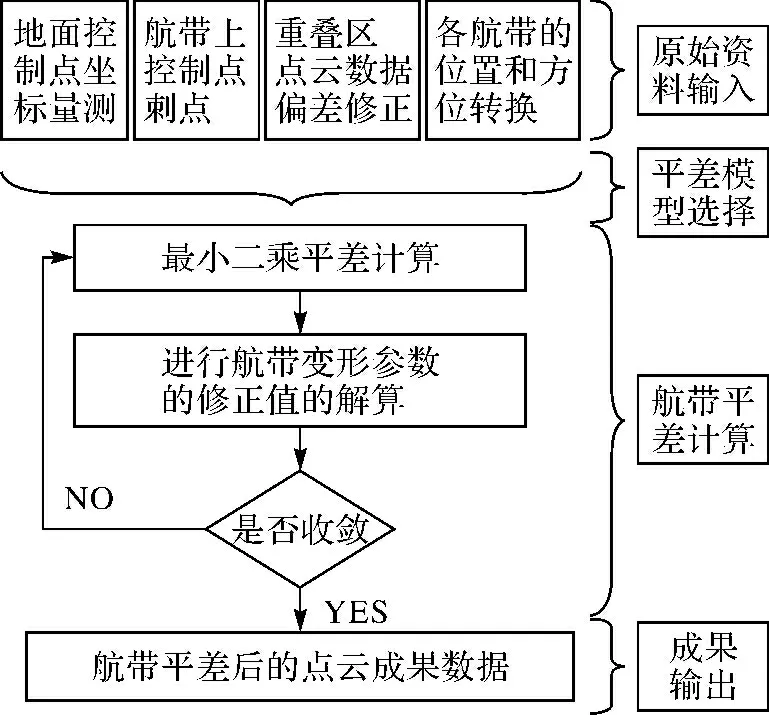
图3 航带平差处理流程
二、数据获取情况
数据获取采用运五飞机作为航空遥感平台,机载LIDAR系统采用Leica公司生产的ALS50-II激光断面扫描系统,其最大脉冲为150 kHz,最大回波次数为4次,扫描频率可达90 Hz。实践研究区由5条航线构成,平均点云密度2个点/m2,平均地面分辨率优于20 cm。通过检校场的飞行和地面测量,完成了对点云数据的初步检校工作,经检校后,数据高程方向平均差为0.012 m,最大差值为0.112 m,最小差值为-0.074 m,均方差为0.036 m,标准差为0.034 m。
三、对比结果与分析
以实践研究区的五条航线数据的平差试验为例,在无地面控制点情况下分别以整体三轴姿态偏移d r、d p、d h和各航线高程调整为未知参数进行解算,得到的参数修正量见表1、表2。
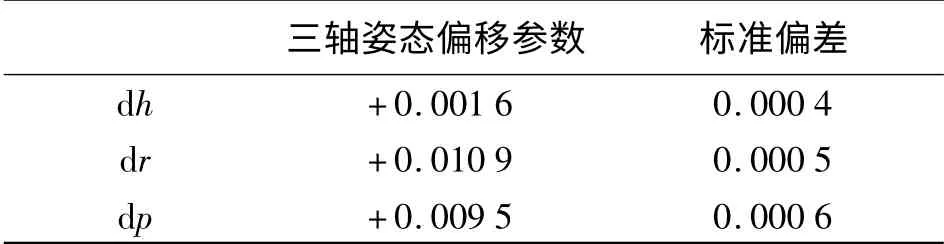
表1 整体参数解算结果 (°)

表2 各航线调整参数解算结果 m
内部精度分析主要在于讨论航带重叠区高程资料的吻合程度,航带重叠区点云资料经地面点分类后,比较所有的共轭地面点的水平距离magnitude大小和高程差异Δz(见表3),结果显示平差处理能够显著降低航带间的水平和高程差异,其剖面点云在平差前后修正情况如图4所示。
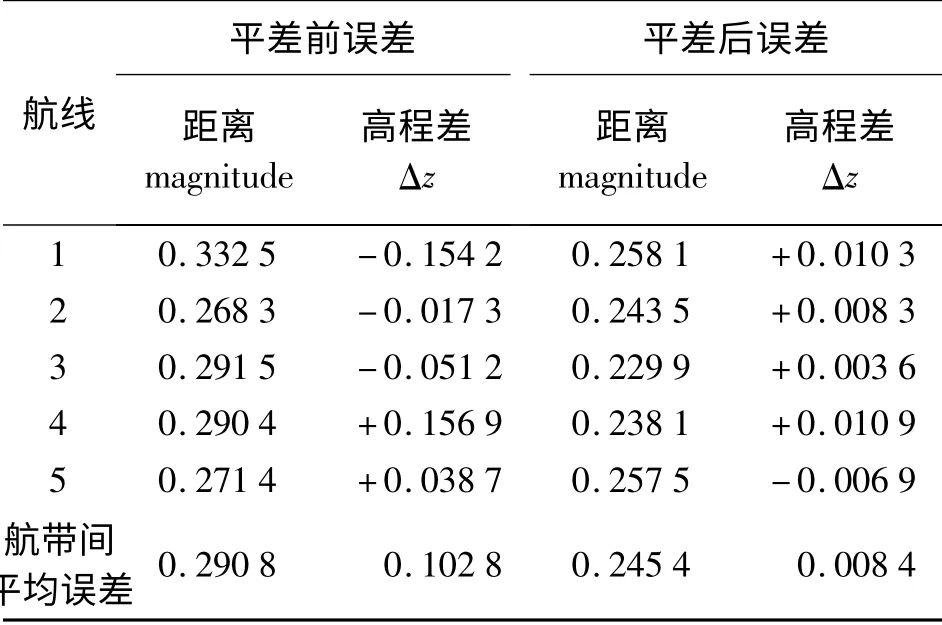
表3 航带平差处理前后误差评价 m
上述平差处理结果表明,机载激光雷达扫描航带间平面误差可达30 cm以上,高程误差可达15 cm,对于大面积多航带激光雷达扫描测量,航带平差具有必要性。需要注意的是,前人的相关研究证明,无地面控制点条件的航带平差结果,虽能消除航带间的相对高程差异,但对于其绝对高程精度没有绝对帮助,有时还会引起误差增大的负效应,因此在平差前要妥善评估。一般对于航带间高程差在5 cm以内的航线,在无地面控制点情况下建议不进行航带平差,以免发生提升了内部精度却降低外部精度的情况。对于大面积机载激光雷达扫描作业,建议引入分布均匀的适量地面控制点进行全区航带平差,以确保高程绝对精度。

图4 航带平差前(a)后(b)重叠区偏差的改善
这里用本次工作中的研究实例具体说明这个问题:由于本次飞行的地面控制点集中布设在实践研究工作区内,对该地区的机载激光雷达数据进行航带平差时就可以引入地面控制点资料。试验结果(见表4)表明,不论航带平差处理中是否引入地面控制点资料,都会对数据的内部精度得到大致相同的改善效果。
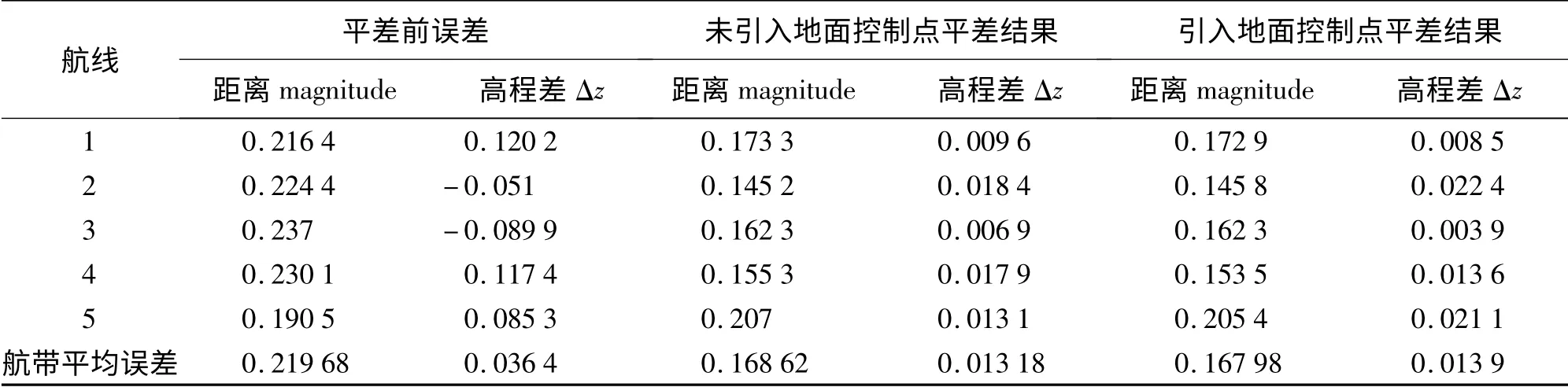
表4 航带平差处理前后内部误差评价 m
但对两种平差结果进行绝对高程精度评价的结果见表5和表6,引入控制点之后的平差结果绝对高程误差为0.119 m,不使用地面控制点的平差结果为0.218 m,而平差之前原始点云的高程误差0.197 8 m(见表7)。以上结果说明,在没有利用地面控制点情况下进行航带平差,虽然会改善数据的内部精度,但造成其外部精度的降低;而利用分布合理的适量地面控制点进行平差不仅能够改善数据的内部精度,同时其外部精度也可以得到显著的提升。这可能是因为在不使用地面控制点时,点云的匹配时不用考虑其绝对坐标的偏差,而只用顾及相同地物点点云之间的位置关系,在这种情况下,匹配之后的点云之间相对位置关系肯定得到了提高,消除了因为系统误差造成的航带间偏移,但点云的绝对位置坐标是否改善并不能肯定,这还是需要依靠地面控制点予以校正和检验。因而下一步,利用分布在试验区四角的4个检查点作为控制点,分别进行了有地面控制点和无地面控制点的平差计算,并对绝对搞成精度进行了分析和对比,结果见表5、表6。
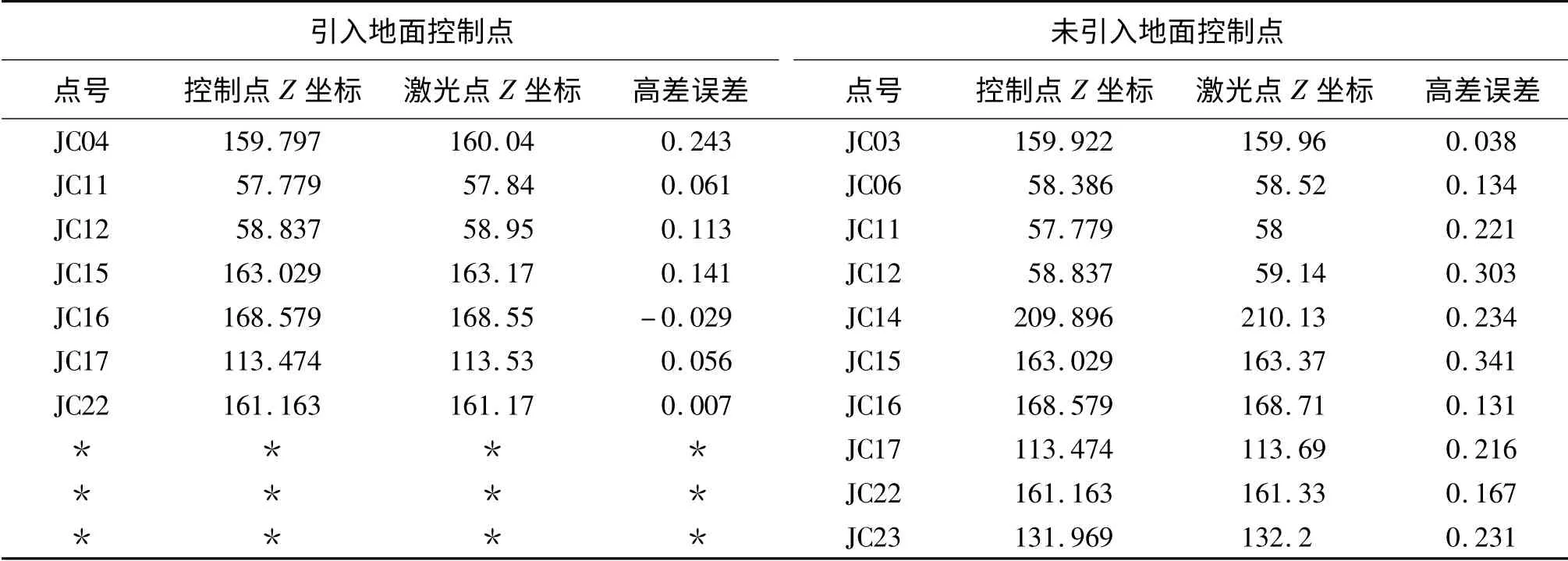
表5 两种平差方式的高程绝对精度对比 m
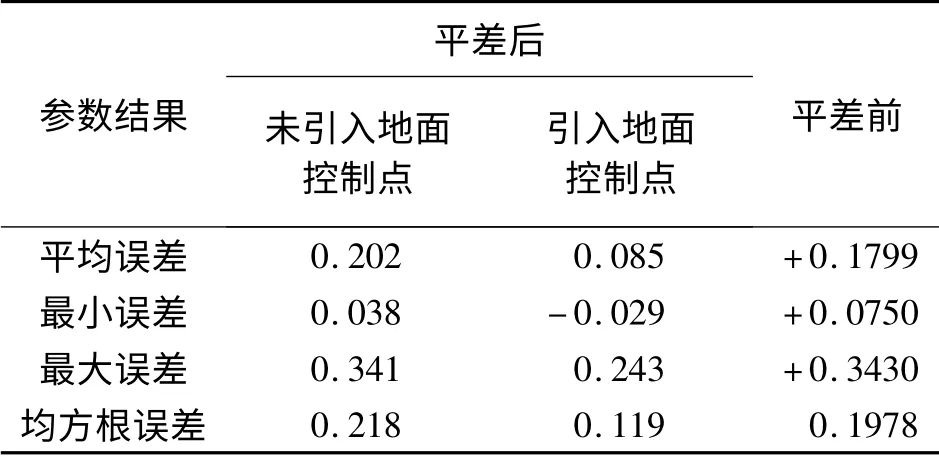
表6 两种方式误差统计结果 m
需要指出的是,本次平差时引入的地面控制点是按照均匀分布的原则,仅选择了试验区内10个控制点中的JC03、JC06、JC14和JC23四点,故在进行高程精度评价时没有采用此四点的对比资料。
四、结 论
对于数据解算过程仍然无法消除的残余航带性系统误差,通常采用航带平差方法进行改善,目前在航带平差时,即使不采用地面控制点,平差后的点云匹配结果仍较理想,且与采用了地面控制点的校正效果有一致性。但无地面控制点的航带平差对于数据整体精度的提升程度未完全确定,在对比了使用和不适用地面控制点两种方式的航带平差的绝对高程结果说明,不使用地面控制点的航带平差虽然提高了点云的内部匹配精度,但绝对定位效果并不理想,高程精度甚至还没有未平差之前高。因此,在对绝对地理位置要求不高、需要快速成图的情况下,可进行无地面控制点的航带平差以获得内部相对位置精度提升的目的。
[1] 张小红.机载激光雷达测量技术理论与方法[M].武汉:武汉大学出版社,2007
[2] 邬建伟.机载LIDAR系统检校和航带平差方法研究[D].武汉:武汉大学,2008.
[3] Leica Company.ALS60 User Manual v0.90[DB].Leica,2009.
[4] BURMAN H.Adjustment of Laserscanner Data for Correction of Orientation Errors[J].International Archives of Photogrammetry and Remote Sensing,2000,33(B3):125-132.
[5] MORIN K,EL-SHEIMY N.A Comparison of Airborne Laser Scanning Data Adjustment Methods[C].∥ISPRS WGII/2 Three-Dimensional Mapping from InSAR and LiDAR Workshop Proceedings.Banff,Alberta,Canada:[s.n.],2001.
[6] VOSSELMAN G,MAASH G.Adjustment and Filtering of Raw Laser Altimetry Data[C]∥Proceedings of OEEPE Workshop on Airborne Laserscanning and Interferometric SAR for Detailed Digital Terrain Models.[S.l.]:OEEPE Publications,2001,40:62-73.
[7] KILIANJ,HAALA N,ENGLICH M.Capture and Evaluation of Airborne Laser Scanner Data[J].International Archives of Photogrammetry and Remote Sensing,1996,31(B3):383-388.
[8] BURMAN H.Laser Strip Adjustment for Data Calibration and Verification[J].International Archives of Photogrammetry and Remote Sensing(IAPRS),2002,34(3A):67-72.
