一种K－均值聚类的改进算法及其应用

江京亚，郭庆胜，陈 旺，周贺杰，陈 勇

（1．武汉大学 资源与环境科学学院，湖北 武汉430079；2．湖北省鄂东地质大队，湖北 孝感432000）

聚类分析是人类理性认识自然，科学分析世界的主要手段之一。自1994年，李德仁院士在国际上首次提出空间数据挖掘与知识发现（Knowledge Discovering and Data Mining）这一概念以来，聚类分析在信息领域得到空前发展，至今已成为空间数据挖掘与知识发现的主要技术手段之一［1］。近十年来，聚类分析已经成为数据挖掘中的一个热点，得到广大学者的关注。综合国内外多年的研究成果［1－5］，聚类分析常用的算法基本可分为基于划分的算法、基于层次的算法、基于密度的算法、基于图论的算法、基于模型的算法、基于格网的算法及其混合算法等七类方法［1］。

K－均值聚类是一种基于划分的经典聚类算法，由于其简单、高效，已被广泛应用于诸如图像处理、模式识别、人工智能和市场销售等领域。然而K－均值聚类其本身却存在很多缺陷，如对初始聚类中心的依赖性和对少量噪声点的敏感性。本文正是为了较好克服这两方面的缺陷，基于k－dist图（又称第k邻近距离图）提出了一种改进K－均值聚类算法。通过数据集的第k邻近距离图，获得噪声范围去除噪声点，同样地在第k邻近距离图中取得点聚集区域范围，从中选取距离相距最远且尽量靠近真实簇中心的k′（为了区别第k邻近距离图中的参数k，聚类类别数用k′表示）个数据点作为初始簇中心。实验证明改进算法能很好地去除噪声点影响，减少迭代次数，得到稳定的聚类结果。

1 K-均值聚类算法

K－均值聚类算法是应用最为广泛的一种空间聚类方法［4］，其基本思想是：在数据集范围内，随机选取k′个对象作为初始簇中心，然后将数据集中每个对象分配到离它最近的初始簇中心分为一类。处理完后，整个数据集暂时被划分为k′个簇，更新簇中心（一般是取此簇中所有对象的平均值），重复上述步骤直到达到一定迭代次数或满足一定的平方误差准则为止。

K－均值算法由于是在数据集范围内随机选取初始簇中心，难以正确反映数据集的性质，聚类结果波动较大，稳定性差。与此同时，在更新簇中心时，采取簇内所有对象的平均值，少量远离数据聚集区的噪声点的加入会使计算结果产生误差，偏离真正的聚类中心，较大地影响聚类结果，甚至可能产生不准确的结果。

近些年，针对K－均值聚类算法对初始中心的依赖性和对噪声点的敏感性，许多学者提出了改进算法。文献［2］在K－均值算法引入混合粒子群优化算法思想，将k′个聚类中心整体作为一个粒子，寻找最优解得到聚类结果。该方法能改善K－均值聚类对于初始聚类中心依赖的缺陷，加快收敛速度，具有很好的全局寻优能力。文献［3］基于高密度区域数据被低密度区域数据所分割的思想，从高密度区域选取k′个相距最远的点作为初始聚类中心，能很好体现数据的分布情况，消除算法对初始聚类中心的依赖。文献［4］用迪杰斯特拉最短距离作为数据对象之间的距离，初始中心选择距离和平均值最小的数据对象，进行K－均值聚类。该方法能消除噪声点的影响，取得较好的聚类结果。这些改进算法虽在一定程度上克服某一方面的缺陷，如对初始中心点依赖性，但无法兼顾噪声点影响，或者消除噪声点，初始聚类中心选取却无法顾及，而且实现起来都比较复杂。

2 第k邻近距离图

在待聚类分析的数据集中，计算每个数据对象离它最近的第k个数据对象的距离（文章后面就称第k邻近距离），然后将此距离序列降序排列，绘制成一个折线图，即为第k邻近距离图，图1为人工数据集Point1及其第4邻近距离图。横坐标代表第k邻近距离排序后的点序列号（和实际读入的数据序列顺序不同），纵轴代表横轴序列点所对应的第k邻近距离。

第k邻近距离图最早是由Martin Ester［5］等为确定一种密度聚类－DBSCAN方法的邻域半径参数而做的图，曲线走向变化较大的那个数据对象所对应的第k邻近距离即为邻域半径（如图1（b）中箭头所指的纵坐标值）。第k邻近距离图能很好地反映一个数据集的分布情况。曲线从左边以陡峭的趋势快速下降到一个临界值－临界第k邻近距离，然后以较小的第k邻近距离趋于平缓，即为数据聚集的地带。由于噪声点数量少，分布离散，因此从左边开始下降速度较快，呈陡峭形势，而在数据聚集区域，数据对象的第k邻近距离都相对较小，较为集中，曲线呈平缓趋势。数据对象的第k邻近距离越小，其为簇中心的可能性越大，反之，其为噪声点的可能性越大。

文献［5］研究发现，第k邻近距离图中当k＞4时，如k＝8，绘制出来的曲线整体趋势与k＝4绘出的曲线变化很小，因此本文取k＝4。

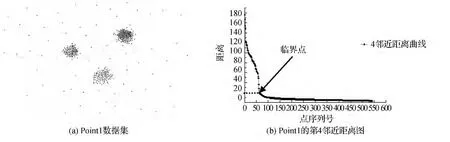
图1 Point1数据集及其第4邻近距离图

3 改进后的K-均值算法

3．1 算法思想及流程

做出数据集的第4邻近距离图，由于数据对象的第4邻近距离越小，其为簇中心的可能性越大，反之，则其为噪声点的可能性越大，因此需要找出噪声临界点（曲线趋势显著变化的那个数据点）所对应的第4邻近距离（称临界第4邻近距离），然后从数据集中清除那些第4邻近距离大于临界第4邻近距离所对应的数据点，得到整理后的数据集。接着在第4邻近距离图中平缓带（数据点密集段）所对应的数据点集中选取相距最远的k′个数据点作为初始簇中心，然后按照最近距离将各个数据分配到离它最近的簇中心，更新簇中心，直到达到一定迭代次数或满足一定的误差平方准则为止。

改进算法主要是基于第4邻近距离图，获得噪声范围去除噪声点，然后选取尽量靠近数据聚集区的k′个初始簇中心，因此迭代次数少，聚类稳定，同时消除噪声点的影响，所得结果较好。

3．2 去除噪声点

噪声点往往是远离数据聚集区的孤立点，数量不多，因此处在4－邻近图中陡峭的一段中。做出第4邻近距离图后，找到临界第4邻近距离，将此距离作为数据点的第4邻近距离的阈值，去除那些第4邻近距离大于该临界第4邻近距离所对应的数据点，即得到去噪后的数据集。

输入：含n个对象的待聚类数据集P

输出：去噪后数据集P1，第4邻近距离图

具体步骤如下：

1）读取数据集P，计算P中每个数据对象pi（i＝1，2，3，…，n）的第4邻近距离，并存储在temp Dist（pi）中。

2）将temp Dist（pi）降序排序，并制作出第4邻近距离图。

3）顺序计算图中相邻3点之间的转角ɑ，找到最大转角ɑ所对应的数据点，将该数据点设为临时临界点，然后依据第4邻近距离图人工判断其合理性，若不符合数据分布特征，则重新指定。确定该临界点的第4邻近距离为临界第4邻近距离dist－Threshol d（如图1（b）中箭头所指临界点所对应的第4邻近距离）。

4）将每个数据点的第4邻近距离与dist－Threshol d比较，若大于或等于dist－Threshol d，则该点是噪声点，从P中删除该点，否则保留此点。

5）处理完所有数据后得到去噪后数据集P1，同时将第4邻近距离图保留下来。

如图2所示，对于数据集Point1，选用传统K－均值聚类算法处理得到的多个聚类结果中较好的一个，如图2（a）中所示，其最终生成的3类簇中包含大量噪声点，簇的中心（图2（a）中十字架所在位置）也偏离了真正的簇中心，而采用本文方法得到的结果，则去除了噪声点只保留了数据点聚集的3个簇，簇的中心也在数据集正中间，聚类效果较好。但是必须注意到很多数据的分布并不是很理想化，即数据聚集区和噪声点可以明显区分开，很多数据簇的界线是模糊的，如图3所示，此时将最大转角a对应的数据点设置为临时临界点，依据第4邻近距离图，发现其并不合理，应顺序后移重新设置临界点，而其第4邻近距离作为临界第4邻近距离。

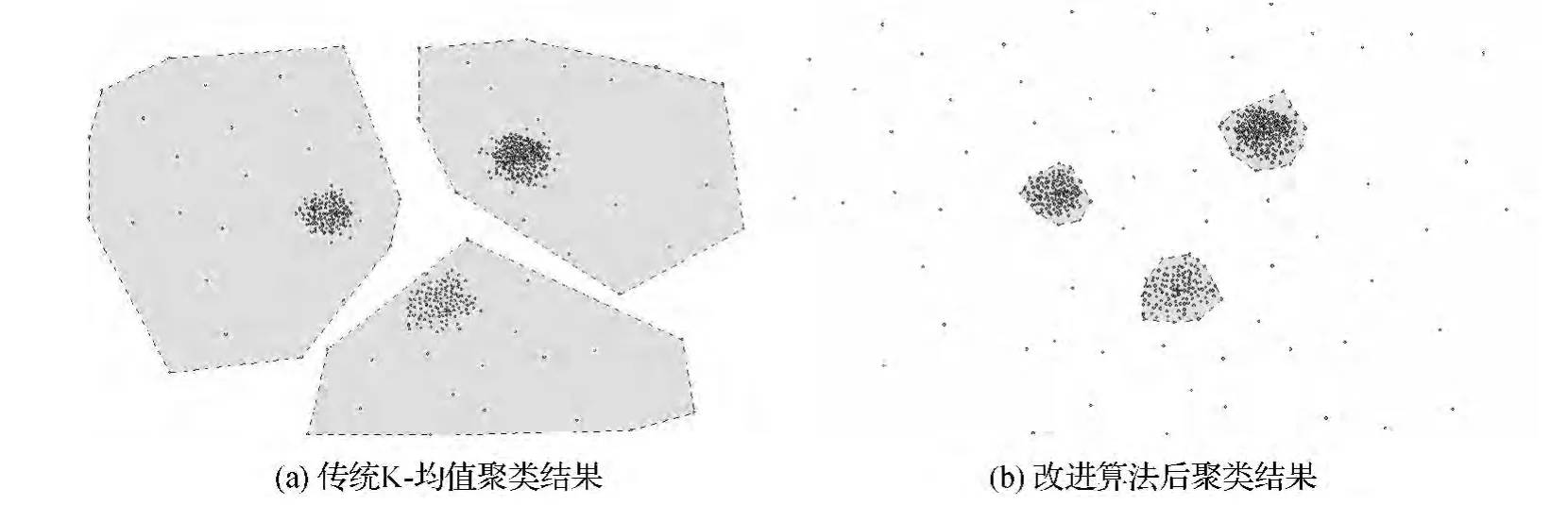
图2 传统K-均值聚类与改进K-均值聚类结果比较

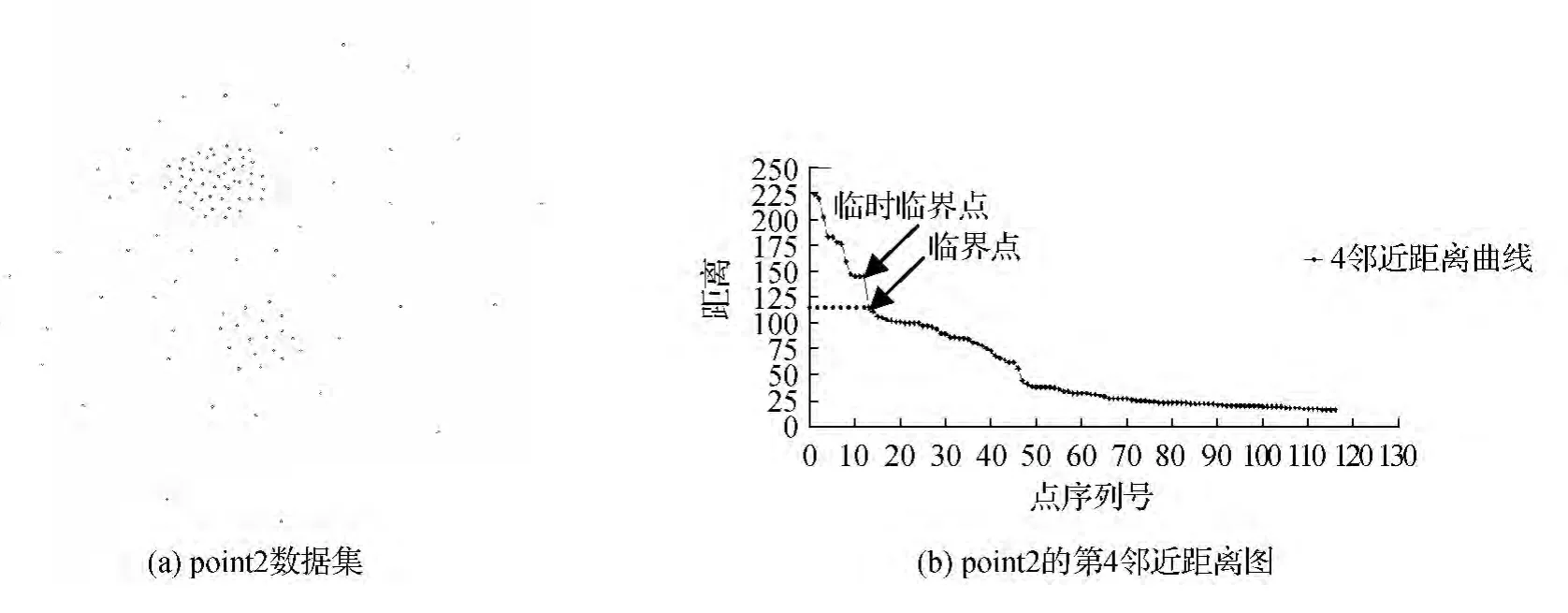
图3 point2数据集及其第4邻近距离图

3．3 k′个初始簇中心的确定

经过去噪后的数据集P1没有噪声点的干扰，可以开始进行K－均值聚类。在第4邻近距离图中找到数据点密集分布的那个平缓带，提取第4邻近距离的范围C（事实上在去噪的同时提取第4邻近距离的最大值和最小值），找到第4邻近距离在此范围内的数据集P2，取最小的第4邻近距离所对应的那个点作为第1个初始簇中心k′1，然后在数据集P2选取离k′1最远的数据点作为第2个初始中心k′2，同理第3个初始簇中心k′3选取离k′1，k′2最远的点，以此类推直到k′个初始簇中心都找到为止。

输入：去噪后数据集P1，聚类个数k′

输出：k′个初始簇中心集合

具体步骤如下：

1）利用去噪时制作的第4邻近距离图，找出数据点密集分布的平缓带C，其中第4邻近距离dist－Threshol d可作为C的上界，下界则为最小4－邻近距离。

2）从数据集P1中选择第4邻近距离在C段的数据点，完成选择后得到数据集P2。

3）将最小第4邻近距离所对应的数据点作为第1个初始簇中心k′1，在P2中找到距离k′1最远的数据点作为第2个初始簇中心k′2，同理，第3个初始簇中心k′3选取离k′1，k′2最远的数据点，即得到的k′3与k′1，k′2之间的最小距离最大。以此类推，直到找到k′个初始簇中心。

4）输出k′个初始簇中心集合。

图4即为数据集Point1的初始簇中心选择，十字架所在位置即为初始簇中心，图4（b）是改进后的K－均值聚类方法选取的初始簇中心，初始簇中心已经很靠近数据点聚集区了，迭代次数少，聚类稳定，而图4（a）则是传统K－均值算法中选取的初始簇中心，它们已经偏离了真正的数据聚集区，增加了迭代次数，产生的结果也有误差。

图4 改进前后K-均值聚类初始簇中心

4 实验结果及其应用

数据来源于网络爬虫软件在2013年6月采集到的47个类型130 683个兴趣点集，本文从中选用了属于河北省张家口市，类型为“小区”的251个子点集，每个数据点包含9个属性，共有3个聚类。运用本文改进的K－均值聚类算法后得出的实验结果见图5。

图5 改进算法后所得结果

从图5可以看出，改进算法去除了少量的噪声点（图5（a）中三角板所在位置），获得了3个主要小区点密集分布区域（图5（b）中3个斑块，也是点集的凸包），效果较好。由于传统的K－均值聚类处理该数据集的不稳定性，进行了10次实验，取其迭代次数平均值（见表1），为3．6次，而采用本文算法只需迭代2次，实验结果也比较满意。在运行时间上，传统K－均值平均运行1 367．9 ms，而本文算法只需738．6 ms，效率提高了46%。这是由于改进算法选取的初始簇中心是尽量靠近点集密集区的数据点，离真正的簇中心很接近，聚类迭代次数少，只需2次就能完成聚类，实验结果稳定，效率高。

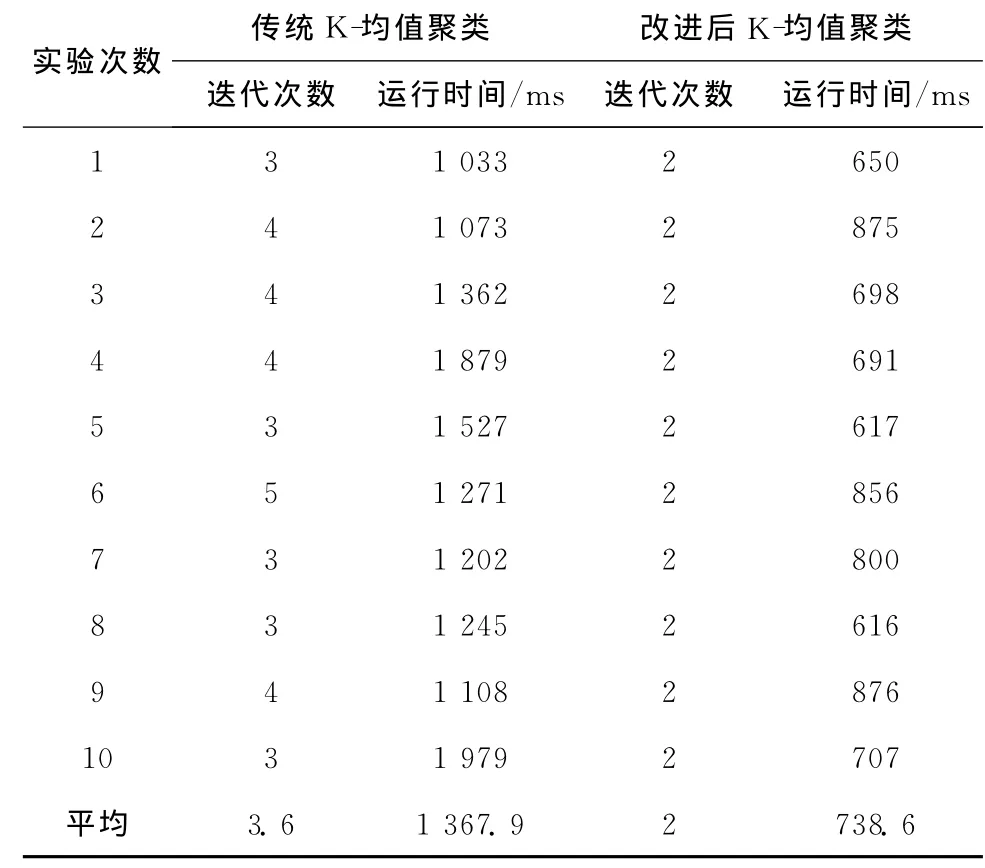
表1 改进前后K-均值聚类算法迭代次数和执行时间

聚类分析是信息挖掘的有效工具之一。通过K-均值聚类分析居民居住小区的聚集区域，往往可以得到很多信息。例如，选址一直是关系经营者盈利与否的关键问题［6］，商场建在那里才能保证人流量足够大，当然也可以结合小区周围的商场、超市等数据点一起分析，怎样才能确定既不和其它商场或超市冲突又能保证足够客流量的最佳位置。利用本文改进的K－均值聚类算法对小区数据点去噪，聚类得到3个小区点数据集，进而生成3个数据集的凸包，得到小区密集区域，即居民常住区域，可以直观地观察到居民的生活范围。为居民提供服务的行业，如餐厅，服装店，商场、KTV等等可以选择在其周围建立，保证其利润最大化。同时，本文提出的算法也可以用来确定传染病重症区，合理安排救治人员；划分旅游景点聚集区，规划最佳旅游路线等等，实用性较好。

5 结束语

针对K－均值聚类对初始簇中心选取的依赖性和对噪声点的敏感性，基于第k邻近距离图，提出了一种改进的聚类算法。该算法去除第k邻近距离较大的噪声点后，选取处于第k邻近距离图中平缓带－数据点密集区中的k′个相距最远的数据点作为初始簇中心。实验证明了改进后算法迭代次数少，聚类稳定，所得结果理想。与此同时，结合实际应用，验证了本文算法的实用性，希望能为选址、规划等一些特定问题决策提供参考。

［1］邓敏，刘启亮，李光强，等．空间聚类分析及应用［M］．北京：科学出版社，2011．

［2］但汉辉，张玉芳，张世勇．一种改进的 K－均值聚类算法［J］．重庆工商大学学报：自然科学版，2009，26（2）：144－147．

［3］傅德胜，周辰．基于密度的改进K均值算法及实现［J］．计算机应用，2011，31（2）：432－434．

［4］仇新玲．K－均值聚类算法改进及应用［D］．北京：北京邮电大学，2012．

［5］ESTER M，KRIEGEL H－P，SANDER J，et al．A densitybased algorit h m for discovering clusters in large spatial databases with noise［C］／／KDD－96：Proceedings of 2nd Inter national Conference on Knowledge Discovery and Data Mining．Menlo Par k：AAAI Press，1996：226－231．

［6］付金辉，赵军喜，高源．基于灰色预测法的超市选址模型研究［J］．测绘工程，2013，22（5）：46－50．

［7］WANG M，WANG A P，LI A B．Mining spatial－temporal clusters fro m geo－database［J］．Lect Notes Artif Intell，2006，4093：263－270．

［8］殷君伟．K－均值聚类算法改进及其在服装生产的应用研究［D］．苏州：苏州大学，2013．

［9］郑丹，王潜平．K－Means初始聚类中心的选择算法［J］．计算机应用，2012，32（8）：2186－2188．

［10］刘艳丽，刘希云．一种基于密度的 K－均值算法［J］．计算机工程与应用，2007，43（32）：153－155．