基于HJ－1B影像的内蒙古草地叶面积指数反演

杨灿灿，吴 见，王 春，邓岳川

（滁州学院 地理信息与旅游学院，安徽 滁州239000）

叶面积指数（LAI）是生态系统，全球碳循环和气候变化等研究的关键参数，而且作为描述植被冠层几何结构的植被特征参数可用于反映植被冠层结构变化和植被生长过程，确定水氧交换率等［1］。庄东英等利用归一化植被指数进行反演LAI并且作为模型参数用于预测小麦生物量［2］。刘照言等基于多光谱遥感利用SAIL模型进行叶面积指数的反演［3］。包刚等对草地LAI进行高光谱数据的反演研究，取得较好的效果［4］，江淼，吴国训等分别对植被覆盖及植被LAI进行了反演并进行尺度变化和时空特征分析［5－6］。王强等人利用IDL处理CHRIS多角度数据并实现森林叶面积指数的反演［7－8］。韩桂华等人根据不同遥感数据选择不同的合适的模型并建立相应的查找表反演LAI，其结果表明多角度数据反演准确率有一定的提高［9］。杨飞等利用环境星影像和T M影像进行LAI的反演并对结果进行对比分析［10］。另外，研究表明，热点区域包含丰富的冠层结构信息，暗点包含有叶片的聚集信息，利用热点效应可以进行准确推断，获取叶片的大小形状及LAI等参数［11］。赵娟等人采用归一化热暗点指数反演不同株型小麦的LAI，并证明多角度遥感数据在作物结果参数提取方面更具优势［12］。内蒙古位于我国北部边疆，是我国最大的草场和天然牧场。估测草地LAI对于掌握其区域草地的生长状态，了解其空间分布格局，对合理利用草场，保持其特色发展其经济具有重要意义。本文基于HJ－1B卫星影像，应用植被指数模型、PROSAIL模型以及在此基础上引用热暗点指数与植被指数构建模型的思想对内蒙古草原的LAI进行反演研究，并对反演结果进行验证和分析。

1 数据和研究区介绍

实验区位于内蒙古自治区贡格尔大草原，属于蒙古东部大兴安岭西麓波状高平原地带经度约为E116°48′，纬度为 N43°24′。该区草地类型以禾草、羊草、杂草群落为主，受地理环境和气候特征的限制，生态具有脆弱性和易损性，在气候、植被和土壤等方面是中国温带半干旱草原典型区域，在内蒙古地区具有较为广泛的代表性，实验区影像见图1。

图1 实验区影像

本实验采用的野外数据通过LAI－2000仪器实地测量获得；量测时选取了30个样地，每个样地的大小为30 m×30 m，每个样地又选3个小区域，大小为10 m×10 m，每个小区域测量的A（冠层上方测量数据），B（冠层下方测量数据）数据利用CV2000进行处理，得到可用的LAI数据。本文将实测点以7∶3的比率分成两组，70%的实测点进行模型的建立与模拟，30%的实测点用来检测叶面积指数反演的精度，参与模型统计的样点数为20个。测量时间在2012年7月29日～2012年8月6日。因云雾影响，本次试验选取2012年8月9日HJ1BCCD卫星影像，并对此影像进行几何纠正，辐射定标和大气校正等。

2 反演模型的建立

2．1 统计模型

统计模型是将可表达光谱特征的量（如植被指数、波段等）和植物的生物量参数（如叶面积指数、叶绿素含量等）通过实验数据联系起来，建立某种相关性关系，进而利用这种相关关系进行叶面积指数的反演。本文选择抗大气阻抗植被指数（ARVI）建立反演模型，ARVI的表达式为

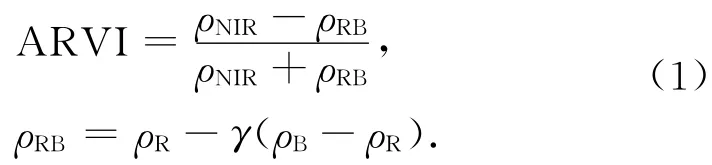
式中：ρR，ρB，ρNIR分别为红色、蓝色和近红外波段的反射率；γ为阻尼系数，当气溶胶含量变化时，用于保持指数的稳定性。抗大气植被指数与LAI之间的关系如表1所示。

表1 ARVI与LAI之间的关系

从线性、二次多项式、幂函数、指数函数四种回归模型中可以看出，ARVI与LAI有较强的关系。但在四种关系统计模型中，相关性最高的二次多项式模型R2＝0．717 5，最低的线性模型R2＝0．69，而RSME的值则以指数模型最低，线性模型最高，但相差不大，所以选择二次多项式模型作为本文的植被指数反演模型。

2．2 PROSIAL反演模型

PROSAIL是在SAIL模型的基础上，建立包含化学组份含量的叶片散射和吸收模型，从而将叶片模型耦合到冠层模型中反演整个冠层的生化组份含量。本研究中，PROSAIL模型中生化参数及土壤背景为试验同步取样后分析结果，并设置时参考LOPEX′93（Leaf Optical Pr operties Experi ment）数据库以及我国典型地物波谱知识库。模型部分参数值设定如表2所示，叶倾角分布选择为球形分布。

表2 PROSAIL的部分输入参数

2．3 热暗点植被指数模型

所谓“热点”，即指观测方向与太阳入射方向同侧即后向散射区域存在的反射率最强点，而“暗点”则正好相反，是指观测方向与入射方向异侧即前向散射区域存在的反射率最弱点。以往的研究表明，反射率在主平面上的变化与日照情况和叶片阴影有很大的关系［10－11］。在同等光照条件下，叶片越聚集，光照叶片的数量越少，这就导致了在不同情况下反射率的差异。这种影响在热暗点指数（HDS）有一定的表现。“热暗点指数”可以被描述为“热暗点差值”与“暗点”的比值，计算时表示为

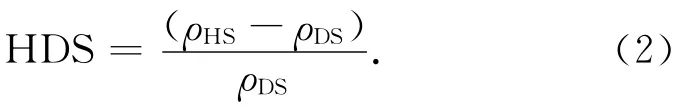
式中：rHS，rDS分别为热点和暗点对应的反射率。显而易见，HDS越高表明“热点”与“暗点”之间的反差越大，这种强烈的反差来自于冠层的粗糙程度，这表明HDS与冠层结构（如叶片空间分布等）有很大的关系，所以在进行植被指数反演时，将热暗点指数和现有的植被指数模型相结合构建了具有二向反射特性的热暗点植被指数模型，其数学表达式为择－35°所在位置对应点，即为暗点，继而可以计算出热暗点指数。

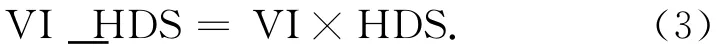
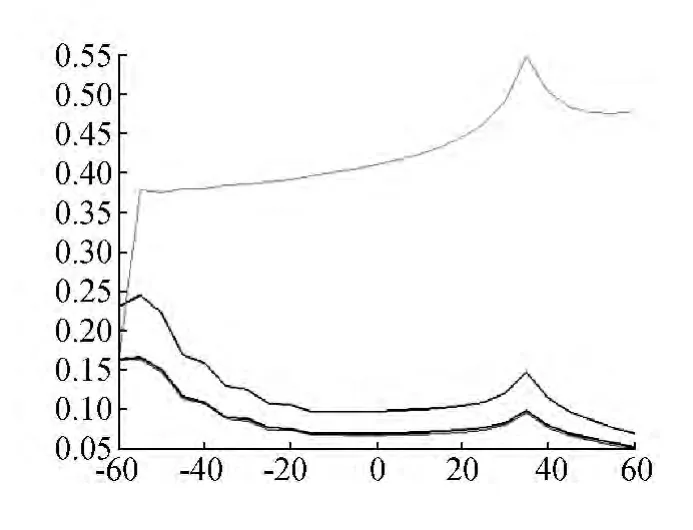
图2 不同波段的二向反射光谱

由于“热点”效应在红光波段和近红外波段比较显著，本文测试了红色、近红外波段热暗点指数（HDS＿R、HDS＿NIR）与LAI之间的相关性度量R2。测试后得到HDS＿R与LAI之间的R2＝0．98，略高与HDS＿NIR。因此，本文用 HDS＿R和NDVI、ARVI分别构建复合植被指数模型，具体形式及与LAI的关系如表3所示。

表3 热暗点植被指数模型关系表

从表3可以看出，加入热暗点指数的模型进行模拟时的相关度与传统的统计模型的相关度要提高很多，从0．7提升到0．89。其中 NDVI－HDS与LAI之间的关系比ARVI－HDS与LAI的关系微强，特别是二次多项式的R2最高，所以本文最终用NDVI＿HDS构建二次多项式热暗点植被指数模型，并应用于实验区LAI的反演。

3 反演结果及分析

3．1 反演结果

统计模型反演LAI结果如图3（a）所示，可以看出整个区域中植被LAI的值集中在1～1．6之间。为验证反演结果，在此区域随机选择了30个实地测量的样本值，其最小值为0．73，最大值为2．1，平均值为1．207 6，这与反演得到的结果在整体上是一致的。从图3（b）中可以看出，利用PROSAIL模型的反演结果碎块比较多，植被LAI的最小值约为0．65，最大值为2，少部分值偏低或者偏高。从LAI集中范围来看，PROSAIL模型的反演结果值的范围与经验统计模型范围大致相同；从最大最小值的角度，PROSAIL模型得到最小值比植被统计模型的最小值大0．05，最大值相差0．2，两种模型的反演结果大体一致。热暗点植被指数模型的反演结果如图3（c）所示。可以看出，LAI的范围在0～2之间，但是植被的叶面积指数在1～1．5范围内占有大量份额，最小值约为0．8，最大值为1．8，与经验统计模型和辐射传输模型的反演结果有差异，但在整体趋势上是一致的。结果图比较整齐，没有太多的碎块，这是因为加入热暗点指数后弱化了零散的地块。

3．2 验证与分析

本文利用30%的实测点检测叶面积指数反演的精度，各指标如表4所示。

表4 LAI验证结果表

从表4可以看出，实测检测点的平均值为1．207 6，传统二次多项式统计模型反演得到的LAI平均值为1．216 8，比实测值高0．099 2；PROSAIL模型反演的平均值为1．267比实测值高出0．069 4热暗点植被指数模型得到的LAI平均值为1．188，比实测值低0．019 6，与实测值最为接近。在与LAI的相关度方面，传统二次多项式统计模型的R2＝0．612 3，PROSAIL模型为0．670 8，复合型植被指数模型为0．700 1；后者与PROSAIL模型比较接近，但略高于PROSAIL模型。在反演的理论精度方面，传统二次多项式统计模型的均方根误差RMSE为0．112 9，PROSAIL 模 型 的 RMSE 为0．076 8，热暗 点植被 指数模 型为 0．089 8，仅比PROSAIL模型低0．013。

图3 各反演模型的LAI反演结果

引入HDS因子的植被指数模型反演后的R2相对于PROSAIL模型没有明显优势，但是其可以避免过多参数的获取。热暗点植被指数模型与传统的植被指数模型相比，其均值比传统植被指数模型反演结果的均值更接近实测值，且相关性R2较高，误差RMSE更小。由此说明引入HDS的统计模型比传统统计模型更适合用来反演内蒙古草地的LAI。

4 结 论

本文分别利用植被指数模型，PROSAIL模型和热暗点植被指数模型对内蒙古自治区贡格尔大草原的LAI进行了定量反演研究。反演结果证明热暗点植被指数统计模型的R2＝0．7，PROSAIL模型R2＝0．67，而传统的植被指数模型R2＝0．61；对于内蒙古草地而言引入热暗点指数的模型反演LAI效果较好，该模型不但与LAI的相关度高，而且对于范围在1～2之间的草地叶面积指数反演也有一定的适应性。但是这三种模型反演的精度普遍不高，可能的原因是：建立的模型和验证的实测数据比较少，从而使模型建立时的统计性不足；影像数据处理产生的残差也是定量反演精度不高的原因之一，有待进一步改善。

［1］ POCOCK M J O，EVANS D M，MEMMOTT J．The i mpact of far m management on species－specific leaf area index far m－scale data and predictive models［J］．Agriculture Ecosystems ＆ Environ ment，2010，135（4）：279－287．

［2］ 庄东英，李卫国，武立权．冬小麦生物量卫星遥感估测研究［J］．干旱区资源与环境，2013，27（10）：158－162．

［3］ 刘照言，马灵玲，唐伶俐，等．基于SAIL模型的多角度多光谱遥感叶面积指数反演［J］．干旱区地理，2010，33（1）：93－98．

［4］ 包刚，覃志豪，周义，等．基于高光谱数据和RBF神经网络方法的草地叶面积指数反演［J］．国土资源遥感，2012（2）：7－11．

［5］ 江淼，张显峰，孙权，等．不同分辨率影像反演植被覆盖度的参数确定与尺度效应分析［J］．武汉大学学报：信息科学版，2011，36（3）：312－315．

［6］ 吴国训，阮宏华，李显风，等．基于MODIS反演的2000－2011年江西省植被叶面积指数时空变化特征［J］．南京林业大学学报：自然科学版，2013，37（1）：11－17．

［7］ 王强，白帆，唐彦，等．利用IDL与VC＋＋联合构建森林叶面积指数反演系统［J］．测绘工程，2012，21（3）：1－4．

［8］ 付海强，汪长城，朱建军，等．一种改进的POLINSAR PCT方法反演植被垂直结构［J］．测绘工程，2014，23（11）：56－61．

［9］ 韩桂华，王强，刘丹丹．基于多角度遥感物理模型的叶面积指数反演［J］．测绘科学，2010，35（3）：77－79．

［10］YANG F，WANG J，CHEN P，et al．Comparison of HJ－1 A CCD and T M data and for esti mating grass LAI and fresh biomass［J］．Journal of Remote Sensing．2012，16（5）：1000－1023．

［11］陈瀚阅，牛铮，黄文江，等．基于热点植被指数的冬小麦叶面积指数估算［J］．农业工程学报，2012，28（1）：167－172．

［12］赵娟，张耀鸿，黄文江，等．基于热点效应的不同株型小麦LAI反演［J］．光谱学与光谱分析，2014，34（1）：207－211．