经典平差函数模型的概括形式分析

刘志平，张书毕，卞和方

（中国矿业大学 国土环境与灾害监测国家测绘地理信息局重点实验室，江苏 徐州221116）

《误差理论与测量平差基础》是测绘专业的八大公共专业基础课之一，该课程教学内容受到高度重视［1－2］。经典平差函数模型已发展为条件平差、附有参数的条件平差、间接平差、附有限制条件的间接平差以及附有限制条件的条件平差模型五种基本形式，但在过去较长时期内沿用平差方法介绍孤立的体系［3］。对此，於宗俦［3］教授提出以附有限制条件的条件平差模型统一各种经典平差模型（为叙述方便，简称於氏概括模型），对引导学生理解各种平差函数模型的区别与联系起到了极大的作用。此外，王新洲［4］教授指出概括平差模型只是在形式上统一各种平差模型，但没有真正揭示各种经典平差模型之间的内在联系，并证明附有限制条件的间接平差即为各种经典平差模型的概括模型（简称王氏概括模型）。

在证明各种经典平差模型的数学等价性方面，王氏概括模型优于於氏概括模型；而在指导测量平差应用中的参数选取等方面，於氏概括模型优于王氏概括模型。例如，文献［4］在证明条件平差模型是王氏概括模型的特例时，设参数个数与观测数相等。这本身只是一个数学推导过程，易使初学者对刚掌握的“观测数”、“多余观测”、“参数”等重要概念产生混淆［5］。鉴此，为进一步在教学过程中突出测量平差理论的核心、反映经典测量平差的研究对象－偶然误差或带有偶然误差的观测值，并在此基础上提出另外一种概括模型形式－等价条件平差模型。

1 於氏概括模型的完备

对于某一平差问题，设观测数为n，必要观测数为t，则多余观测数r＝n－t。r个多余观测必然产生r个关于观测值的一般条件方程。若选用u个参数，且参数之间可以形成s个函数关系式，则必然产生u－s个关于观测值与参数的一般条件方程、s个关于参数的限制条件方程。因此，一般条件方程个数为c＝r＋u－s，限制条件方程个数为s。因此，根据上述平差问题，可形成於氏概括平差模型：

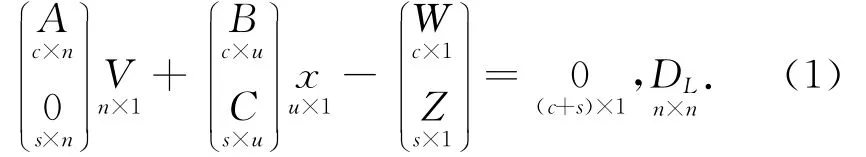
式中：A，B，C为已知的系数矩阵；W＝－（AL＋Bx0＋A0）为具有参数的条件方程闭合差；Z＝－（Cx0＋C0）为限制条件方程闭合差；DL为观测值L的方差阵；V，x分别为待求的残差与参数改正向量。

为保证平差函数模型解估计的存在性，应满足

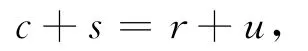
因此，平差模型中的矩阵应满足：A为行满秩矩阵，B为列满秩矩阵或为列满秩矩阵

C为行满秩矩阵。基此，结合三大类参数选取方式，可以获得五种基本平差模型形式，见表1。

表1 完备的平差函数模型

分析三大类参数选取及其对应概括模型中的矩阵性质：

1）当不选取任何参数时，其参数数目u＝0，可建立条件平差模型，即B＝0，C＝0，A为行满秩矩阵的概括模型。

2）选取独立参数，其数目理论上满足0＜u≤t。若0＜u＜t，则可建立附有参数的条件平差模型，即相当于C＝0、A为行满秩矩阵、B为列满秩矩阵的概括模型。若u＝t则可列立间接平差模型，即相当于A＝－I，C＝0。

3）当选取的参数具有函数相关的性质，其数目理论上满足u＞0。若其中参数独立数不超过必要参数个数t，则参数数目u＞0，可列立附有限制条件的条件平差模型，相当于A为行满秩矩阵，¯B为列满秩矩阵，C为行满秩矩阵的概括模型；若其中参数独立数恰好为必要参数个数t，则参数数目u＞t，可列立附限制条件的间接平差模型，即相当于A＝－I，B为列满秩矩阵，C为行满秩矩阵的概括模型。

综上所述，从参数数目u取值范围的角度看，表1描述的经典平差模型是完备的。然而现有文献［6］介绍的附有限制条件的条件平差，对参数数目的要求（0＜u＜t）是不完备的，现有教材对u≥t且其中独立参数少于t的情况没有考虑。对此，曾在文献［7］针对参数u＝t且其独立参数少于t的附有限制条件的条件平差解法进行完善，其思路可以推广至参数取值范围完备的於氏概括平差。

2 等价条件平差模型

讨论参数完备条件下的於氏概括模型，为平差模型应用中的参数选取提供依据，同时也建立必要观测、多余观测、参数等基本概念与测量平差模型的联系。

1）附有参数的条件平差模型、间接平差模型。首先，对任意列满秩矩阵B，其零空间投影算子［8］HB可以仿照平差因子［9－12］得到

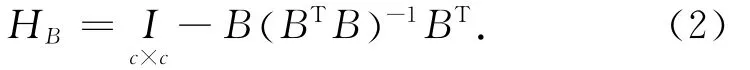
其中，零空间投影算子满足HBB＝0。

进而，对附有参数的条件平差模型、间接平差模型分别左乘上述零空间投影算子HB，便可消去其中的独立参数，由此可得相同形式的条件平差模型

经零空间投影算子HB处理后，上述两种基本平差模型均具有“条件平差模型”的形式。分析零空间投影算子可知，零空间投影算子HB的维数为c×c，由于附有参数的条件平差模型与间接平差模型的限制条件方程个数s＝0，则方程总数为c＝r＋u。另外，顾及到零空间投影算子的秩rank（HB）＝c－u，表明其仅r个行向量相互独立。因此该“条件平差模型”具有r个有效的条件方程。

2）附限制条件的条件平差模型、附有限制条件的间接平差模型。与式（2）同理，令¯BT＝［BC］可得列满秩矩阵B的零空间投影算子 H¯B。

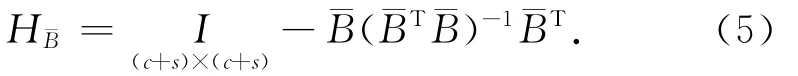
与式（3）、式（4）同理，对附有限制条件的条件平差模型、附有限制条件的间接平差模型分别左乘上述零空间投影算子H¯B，便可消去其中的相关参数，得到相同形式的条件平差模型

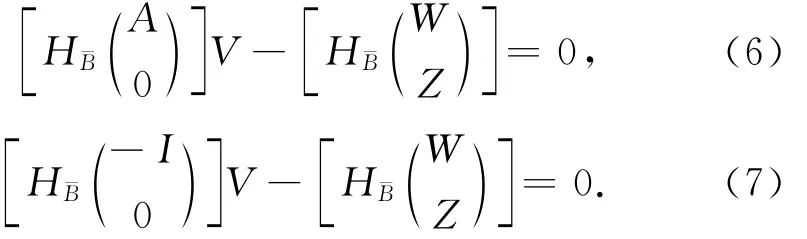
经零空间投影算子H¯B处理之后，上述两种基本平差模型均具有“条件平差”的形式。分别分析两类零空间投影算子可知，H¯B的维数为（c＋s ）×（c＋s ） ，由于附有限制条件的条件平差模型、附有限制条件的间接平差模型具有s个限制条件，则方程总数c＋s＝r＋u。另外，考虑零空间投影算子的秩rank （H¯B）＝c＋s－u，表明其仅r个行向量相互独立。因此该“条件平差模型”具有r个有效的条件方程。

综上所述，式（2）、式（5）实现了四种基本平差模型至条件平差模型的转换，证明了五种基本平差模型的等价性。因此，可将式（3）、式（4）、式（6）和式（7）以等价条件平差模型概括为

由前述分析可知，式（3）、式（4）、式（6）和式（7）的方程个数不少于r，但仅含有r个函数独立的条件方程，即等价条件平差模型。此外，现有的於氏概括模型、王氏概括模型和本文概括形式——等价条件平差模型，从三个不同的角度均对各种经典平差模型进行正确的概括，这本身也证明了各种经典平差模型的等价性。本文仅对包含残差向量V的等价条件平差模型进行概括，该特点便于在教学过程中使学生加深理解平差准则这一核心内容。

实际上，在教学中要强调平差参数的引入仅是源于测量工作的实际需要，所需参数可能是函数相关、也可能是函数独立的，而且参数个数也可因需要确定，但都不影响其平差实质——对偶然误差或带有偶然误差的观测值按最小二乘准则进行调整。换言之，若不考虑实际工作，首先，不选任何参数而建立条件平差模型，之后根据所需参数与观测值的函数关系进行参数估计、以及利用协方差传播律进行参数精度评定。由此可知，本文概括模型凸显了条件平差模型及与其他各种经典平差模型的关系，也加强条件独立与参数独立、平差准则与平差模型等基础概念的联系，易使学生更加深刻理解“同一平差问题的平差结果不因平差函数模型的不同而不同”。

3 结束语

当前，许多学者对各种经典平差模型的等价性及其内在联系作了较为广泛的探讨。本文对比分析於氏概括模型、王氏概括模型的特点，同时从参数数目取值范围的角度，完善於氏概括模型。在此基础上，利用零空间投影算子（或称平差因子）将各种经典平差函数模型转换为等价条件平差模型，由此得出经典平差模型的另一种概括形式。同时指出，等价条件平差函数模型仅包含残差向量，便于加深学生对测量平差研究对象（偶然误差或带有偶然误差的观测值）、经典平差理论核心（最小二乘平差准则）的理解。此外，推导过程中零空间投影算子的应用，可让学生对矩阵运算的重要性留下深刻印象，为学习高等平差做铺垫。

［1］ 邓兴升．提高测量平差课程教学质量的措施［J］．测绘工程，2010，19（3）：74－76．

［2］ 邱卫宁，陶本藻，姚宜斌．误差理论与测量平差基础精品课程的建设与实践［J］．测绘工程，2011，20（1）：77－81

［3］ 武汉测绘科技大学测量平差教研室．测量平差基础［M］．3版．北京：测绘出版社，2007．

［4］ 王新洲．论经典测量平差模型的内在联系［J］．测绘通报，2004，33（2）：1－4．

［5］ 姚宜斌，邱卫宁．测量平差问题中必要观测数的确定［J］．2007，36（3）：14－15．

［6］ 邱卫宁，王新洲．测量平差教学体系的设计与研究［J］．测绘通报，2006，35（2）：67－69．

［7］ 张书毕，秦永宽，陆翠，等．概括平差模型解法的完善［J］．测绘通报，2007，36（11）：7－9．

［8］ 刘志平．等价条件闭合差的方差－协方差分量估计解析法［J］．测绘学报，2013，42（5）：648－653．

［9］ 陶本澡．平差因子与平差结构［J］．大地测量与地球动力学，2002，22（3）：6－10．

［10］刘志平，张书毕．方差协方差分量估计的概括平差因子法［J］．武汉大学学报：信息科学版，2013，38（8）：925－929．

［11］张海霞，陈向阳，赵文普．基于自由网平差的一体化DLG生产试验［J］．测绘工程，2015，24（1）：69－72．

［12］黄志伟，刘晓华，龚率，等．基于三维平差的基坑监测数据处理方案探讨［J］．测绘工程，2015，24（2）：51－54．