相交圆柱圆锥参数化绘图命令的二次开发

胡志刚,胡炜

(1.河南科技学院,河南新乡453003;2.贵州电子信息职业技术学院,贵州凯里556000)

相交圆柱圆锥参数化绘图命令的二次开发

胡志刚1,胡炜2

(1.河南科技学院,河南新乡453003;2.贵州电子信息职业技术学院,贵州凯里556000)

就相交圆柱、圆锥体参数化绘图命令的Lisp二次开发,给出了相交圆柱及圆锥表面的相贯线算法的参数公式和实现参数化绘制三视图程序设计思路,对实现参数化绘图所涉及到的一些关键问题给出相应的处理方法,对绘图命令的不同参数输入及对应的相贯线绘图结果进行分析;该命令以对话框输入初始参数,能实现自动绘制圆柱、圆锥体及其相贯线三视图、尺寸标注及将主要尺寸、参数及相贯线的坐标数据写入数据文件.

二次开发;相贯线;参数化绘图;Lisp

在工程设计中,几何形体建模及图样的绘制是基本的和极其重要的设计环节,回转体是组成几何体模型的基本单元之一,准确建模及绘图,尤其是创建相交的回转体表面交线是关系到回转体建模、绘制多面投影视图和表面展开图的关键,也是设计人员常常遇到的问题.有关文献基于不同的建模与绘图要求给出了相应的数学模型及其程序设计方法,有些是针对轴线相交的情况,有些是针对轴线垂直的情况,有些则是针对轴线处于一般位置的情况[1-3].本文介绍一个基于AutoCAD二次开发的参数化设计与绘图命令,用于圆锥和圆柱体组合建模时处于一般位置的情况,但与一些相关文献对同类情况的具体数学模型在坐标系的选择及表达式的建立上具体方法有所区别,几何意义更为明显,在应用程序的功能设计上更为全面,可以绘制其组合体及其相贯线的多面投影视图、表面展开图,实现尺寸标注,将输入的初始参数和其他重要的数据写入数据文件,为工程设计和制图提供一个有效的工具.

1 圆柱、圆锥交线的数学模型

两个基本回转体相交,其交线只与各自的尺寸和相对位置有关,而与坐标系的选择无关,但呈现的数学表达式在形式上有所不同[2-3].本算法采用两个附着于圆锥和圆柱的笛卡尔坐标系定义各自回转面及其交线,并通过适当的坐标变换将交线分别绘制在各个视图平面及展开面上.

建立一个笛卡尔坐标系O-XYZ,将下圆锥(对顶的上圆锥不显示)顶点置于坐标原点位置,圆锥轴线与Z轴共轴,下圆锥位于XY坐标平面下方,向上为正方向;将圆柱体轴线与Y轴同轴,此时圆锥圆柱轴线正交,锥顶点在圆柱轴线上;当两者处于一般位置时(即圆锥面和圆柱面轴线为异面直线),相当于改变圆柱面及其坐标系的位置,即围绕X轴旋转β角度,再分别沿着X、Z轴移动Δx和Δz而得到,此时Δz一般应为负值,此时随同圆柱面移动到新位置的坐标系用O1-X1Y1Z1表示,这时X和X1方向仍相同,如图1所示.

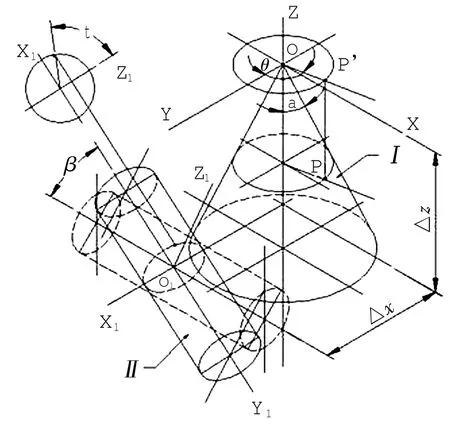
图1 相交圆柱体、圆锥体、坐标系及基本参数Fig.1 Intersecting cylinder and cone,coordinate systems and basic dimensions

2 Lisp程序设计及问题处理方法

开发过程基于Visual Lisp集成开发环境,用Autolisp语言进行程序设计,并基于对话框输入初始尺寸和参数,如图2所示.

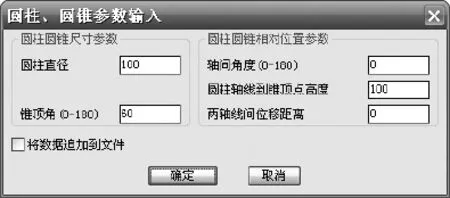
图2 相交圆柱、圆锥参数输入对话框Fig.2 Parametric entry dialog box for intersection of a cone and a cylinder

参数化绘图命令命名为cone_cyl_intersection,命令功能包括在指定点绘制圆柱、圆锥组合体及其交线的主、俯及左视图,在各自回转体视图附近绘制表面展开图,标注各部尺寸,将回转体尺寸、位移参数及交线参数数据写入一个Excel文件[5].主程序和绘图部分程序设计框图如图3所示,在执行主程序绘制视图和展开图时调用画图子函数,左图为主程序框图.

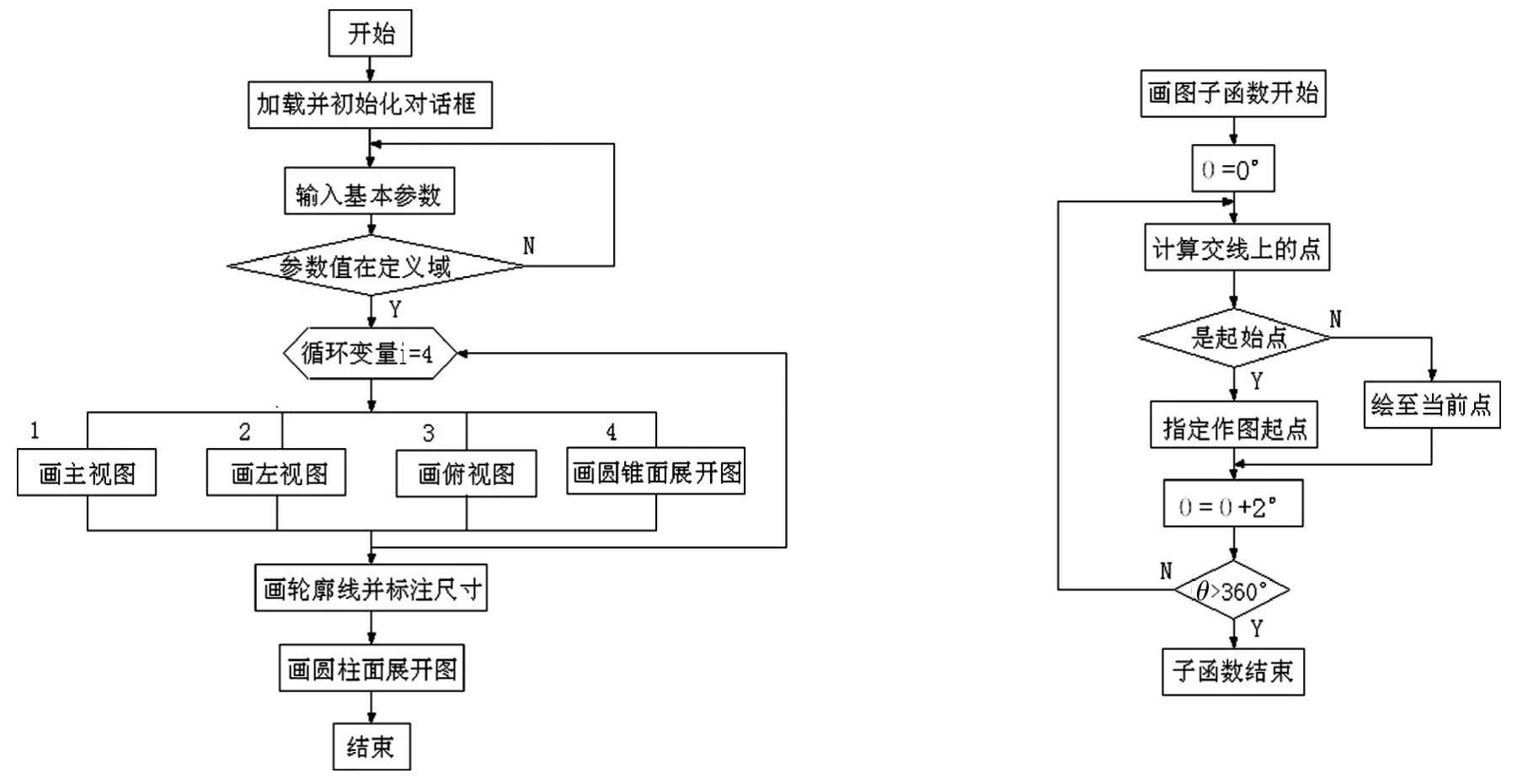
图3 三视图绘制的程序框图Fig.3 Diagram of mutiview drawing program section

2.1 点在构造平面上的坐标变换

由公式(5)、(7)计算出的交线上点的坐标,必须经过坐标变换形成用户坐标系O′-X′Y′Z′的X′Y′构造面上的二维坐标.设计算出点的坐标为P(x,y,z),绘图起始点的坐标为S′(x′0,y′0,z′0),俯、左视图与绘图起始点的距离分别为和e1和e2,其转换公式分别为

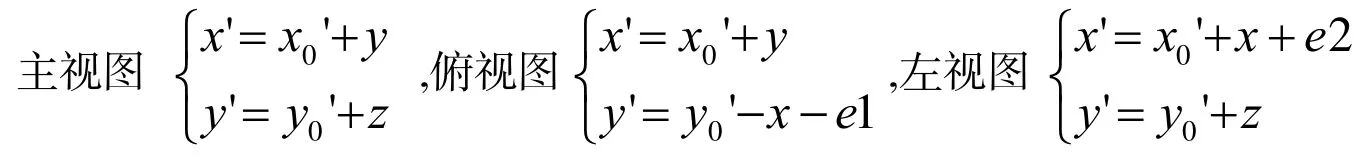
圆锥面展开图的绘图起点可置于主视图左上方,设为A′(x′1,y′1,z′1),根据式(8),其交线展开图上任意一点与用户坐标系X′轴的夹角,该点可用Autolisp中的函数(polar A′ω′ρ)来确定.

绘制圆柱面展开图时,同样需要把交线上的点P(x,y,z)变换到用户坐标系X′Y′构造面上,设绘制圆柱面展开图的起始点与S′点在X′、Y′方向的偏移距离分别为e3和e4,根据公式(7)和(8),坐标变换公式为.

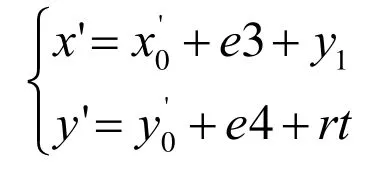
2.2 交线连接点的处理

由公式(5)和(7)可以看出,在计算交线上一点时,一次计算出两个点的坐标(公式(5)的z和公式(7)的y1),当交线包围锥顶点时,同时生成的两条交线分别位于对顶点两边的上、下圆锥面上,一般在工程设计上只保留一侧圆锥面(本文为XY坐标面下侧)及其交线,所以舍弃掉z＞0的交点;当交线处于不包围锥顶点的位置,同时生成的两个交点将形成两段交线,由这两条交线构成一条封闭的交线;由于计算交点是不连续的,其密度随参数步长值Δθ和Δt减小而增加,生成的交线越光滑,但总会在两段交线连接处有间断,如图4所示,除非计算的z或者y1恰好两值相等,在实际计算交点时,可以在接近连接点区域时取足够小的参数步长值Δθ和Δt,并用直线直接两个端点,而在其他交线参数域内取较大的参数步长值,以减少计算量.

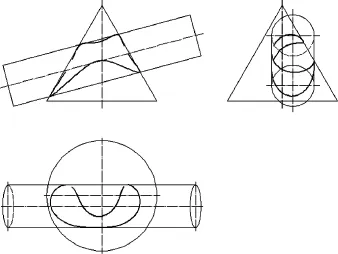
图4 封闭交线在连接点出现间断Fig.3 Breaks at jionts of two sections of a closed intersection curve

3 命令执行及运行结果分析

在程序设计中,将该绘图命令命名为cone_cyl_intersection,加载该命令定义程序,输入命令名后,程序将绘制相交圆柱、圆锥体及其交线的三视图、尺寸标注和圆柱、圆锥表面展开图,同时将原始输入参数及相贯线坐标数据写入数据文件.根据输入的参数不同,图形将反应出圆柱、圆锥相交的各种相对位置关系和对应的交线形状[3].

3.1 轴线平行的情况

两轴线平行时β=90°,所产生的交线分为包围锥顶和不包围锥顶,共轴是包围锥顶的一个特例.当r=25,α=30°,Δx=35,Δz=0时,绘图结果如图5所示为交线包围锥顶的情况;当r=25,α=45°,Δx=0,Δz=0时,绘图结果如图6所示共轴的情况;当r=25,α=30°,Δx=85,Δz=150时,绘图结果如图7所示为交线不包围锥顶的情况.

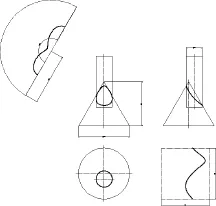
图5 交线包围锥顶点Fig.5 Intersection line around cone apex

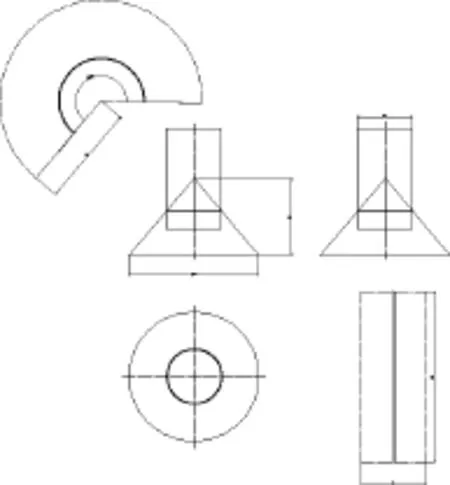
图6 交线包围锥顶且轴线共轴Fig.6 Intersection line around cone apex and coincident

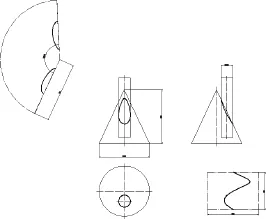
图7 交线不包围锥顶点Fig.7 Intersection line not around cone apex

3.2 轴线相交

轴线相交有表面互贯、圆柱面贯穿圆锥面和圆锥面贯穿圆柱面三种情况,同时根据轴线的交角不同又分为正交和斜交.

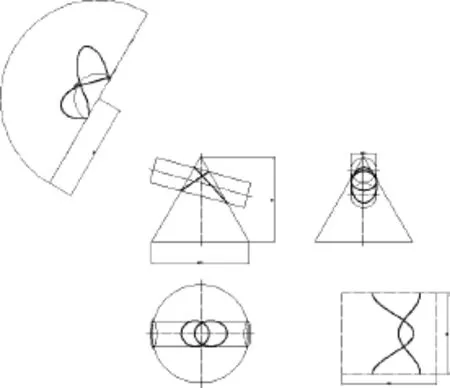
图8 轴线正交时的两曲面互贯的相贯线Fig.8 Intersection line on right intersecting condition

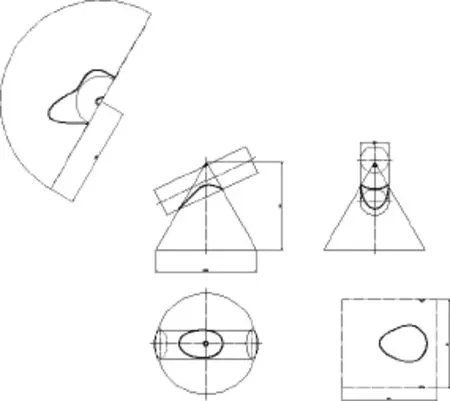
图9 轴线斜交时圆锥面贯穿圆柱面的相贯线Fig.9 Intersection line of cone through cylinder surface at non-right angle

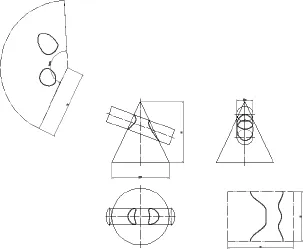
图10 轴线斜交时圆柱面贯穿圆锥面的相贯线Fig.10 Intersection line of cylinder thought cone surface at non-right angle

3.3 轴线是异面直线

圆柱和圆锥的轴线以直角或者一般角度相交且是异面直线时,相贯线一般为单条或两条封闭的空间曲线,此时,参数输入对话框中"两轴线间位移距离"Δx不为0.以下是几种典型的相贯线的形态.

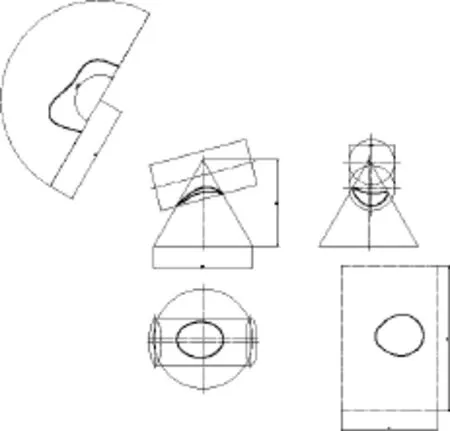
图11 一条交线围绕锥顶点Fig.11 One intersection line around cone apex

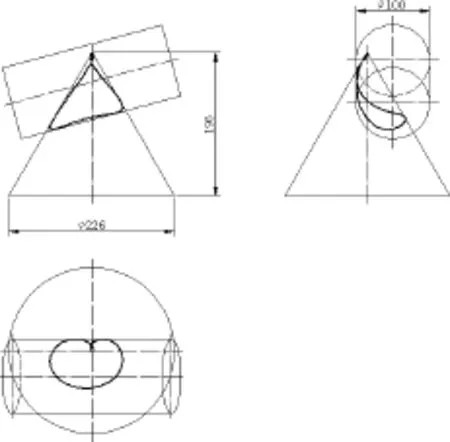
图12 两条交线围绕锥顶点Fig.12 Two intersection line around cone apex

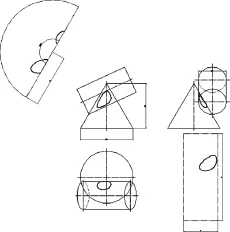
图13 一条交线不围绕锥顶点Fig.13 One intersection line not around cone apex

当β ＜90°−α 时,,且Δx的绝对数值较大时,交线常为一不围绕圆锥顶点的空间封闭曲线,如图14所示;Δx的绝对数值较小时,交线主要呈现为两条围绕圆锥顶点的空间封闭曲线,如图15所示.

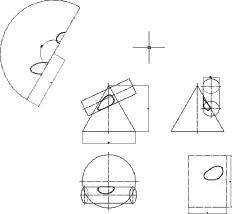
图14 一条交线不围绕锥顶点Fig.14 One intersection line not around cone apex

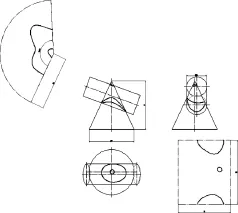
图15 两条交线围绕锥顶点Fig.15 Two intersection line around cone apex

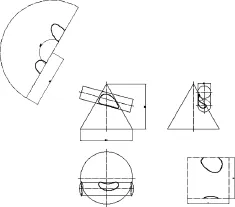
图16 一条交线不围绕锥顶点Fig.16 One intersection line not around cone apex

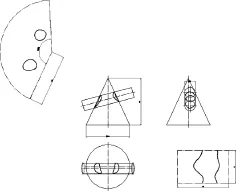
图17 两条交线不围绕锥顶点Fig.17 Two intersection line not around cone apex

当β＞90°−r 时,交线通常为一条空间封闭空间曲线,如图18所示.

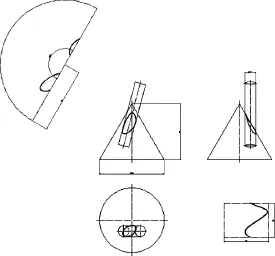
图18 一条交线Fig.18 One intersection line

可以通过更为详细的相贯线状态分析来创建圆柱、圆锥相交的形态图谱,并对每种形态图对应出初始输入尺寸和参数,以便设计和绘图时有针对性的应用[6].

4 小结

应用程序是以圆锥及其附着的坐标系O-XYZ为参照来定义圆柱及其附着坐标系O1-X1Y1Z1的位置,其一般位置可以通过将圆柱及其固连坐标系围绕X轴旋转一定角度,并分别沿着Z轴和X轴移动一定距离而实现,因此不需要使其再围绕Y和Z轴旋转及沿着Y轴平移的变换,从而简化了坐标点的计算量和程序设计.

应用程序可以通过输入不同的初始尺寸、参数来绘制各种相对位置情况下的相交圆柱、圆锥的三视图.该程序没有设计消除隐藏线的功能,在作图时可以使用Trim(修剪)或Break(打断)命令进行消隐,或打断后用虚线表达隐藏线.不同初始参数的对话框输入可以通过对DCL对话框文件及Lisp程序参数输入及对话框处理的相关函数进行少量改动来实现,以适应不同的设计及制图的需要.依据本文提供的相贯线参数计算公式还可以进一步推导出圆柱、圆锥面展开面的相贯线展开公式,从而增加表面展开图的作图功能,方便了钣金图的绘制.

[1]胡志刚,郑秋白.相交圆柱表面展开参数化绘图命令的Lisp二次开发[J].河南科技学院学报:自然科学版,2014,42(5):66-71.

[2]侯爱民.偏斜交圆柱圆锥表面展开图计算机绘制数模原理[J].机械管理开发,2011,121(3):197-198.

[3]高丽华.相交圆柱与圆锥表面展开图的计算机绘制[J].机械设计与制造工程,2001,30(5):45-46.

[4]江苏师范学院数学系.解析几何[M].北京:人民教育出版社,1983:187-208.

[5]胡志刚.大型椭圆形封头放样图参数化绘图的Lisp实现[J].河南科技学院学报:自然科学版,2013,41(5):53-57.

[6]储珺,高满屯.用形态图方法建立圆柱与圆锥相贯图谱[J].机械科学与技术,2003,22(1):63-65.

（责任编辑：卢奇）

Secondary development of parametric drawing command of intersection of a cylinder and a cone

HU Zhigang1,HU Wei2
(1.Henan Institute of Science and Technology,Xinxiang 453003,China;2.Guizhou Vocational Technical Collage of Electronic Information,Kaili 556000,China)

For secondary development of a parametric drawing command of a complex object,which was composed of a cylinder and a cone,the formula of the intersection curve was given and the Lisp program structural diagram of parametric drawing of multiview was delivered,some processing methods coping with several key problems of drawing of intersection curve was listed.Different intersection line result in connection with different parameters'entry were analyzed.The command has the functions of multivew drawing,dimensioning and writing main parameters and coordinate data of intersection line to a data file.

secondary development;intersection line;parametric drawing;Lisp

TP391.7

：A

：1008-7516（2015）05-0058-09

10.3969/j.issn.1008-7516.2015.05.013

2015-06-09

国家自然科学基金(51375149)

胡志刚(1962-),男,江西进贤人,副教授.主要从事机械设计、CAD及工程图学研究.