GM（1，1）模型在区域似大地水准面精化中的应用研究

罗文生，倪 津，施 昆，杨建文

（1．昆明理工大学 国土资源工程学院，云南 昆明650093；2．云南省测绘产品检测站，云南 昆明650034）

灰色模型是灰色系统理论的一个重要分支，自邓聚龙教授首次提出以来，在农业、交通、地质、测绘、金融、生态等众多领域得到了广泛的应用，并取得了丰硕成果，产生了显著的社会效益和经济效益［1－2］。GM（1，1）模型是灰色模型中迄今为止应用最广泛的模型之一，该模型计算简便、实用广泛，因此在灰色预测中占有重要地位［3］。目前国内外在精化区域似大地水准面的常用方法主要有地球重力场模型法和数学模型拟合法。常用的地球重力场模型有EGM96、EGM2008，虽然其分辨率很高，但精度相对较低，并且相应区域的重力数据很难获取，不能满足一般工程建设的实际需要［4］。数学模型拟合法包括曲线拟合法、曲面拟合法、非参数回归法等，其对建模要求较高，并且要根据区域地形特征和对已知点数量的多少来选择相适应的数学模型，在地形复杂、控制点稀少的区域难以建立精确的似大地水准面模型。在缺少重力数据的区域，GM（1，1）模型建模不像一般的函数模型那样，根据地形特征与已知点数量的多少决定选择哪种数学模型更好，在已知控制点稀少，不用考虑地形特征的情况下，GM（1，1）模型建模的效果一样很好。

本文针对GM（1，1）模型建模只需少量数据的优势，利用该模型来拟合高程异常值序列，并在我国地形复杂、交通不便、等级控制点稀少的偏远山区建立了区域似大地水准面精化模型，以充分预测似大地水准面的变化趋势，为工程建设提供保障。

1 似大地水准面精化的原理

近年来，在我国经济发达的中、小城市的地形图测绘中，对厘米级似大地水准面的需求十分迫切，因此区域似大地水准面精化是一个国家或地区建立现代高程基准的主要任务之一［5］。在工程实践中，利用GPS技术可以获取基于WGS－84参考椭球的地面控制点的大地高H，同时利用常规的水准测量方法可以提取基于我国常用的正常高系统上的正常高h 由这两种方式而建立的地面控制点成为GPS水准点。同一GPS水准点的大地高和正常高有如下的关系：

式中ζ称为高程异常。

通常情况下，可通过离散点的高程异常值建立数学模型来拟合区域似大地水准面精化模型，从而求解待定点的高程异常值。高精度的区域似大地水准面所求取高程异常值结合GPS定位技术所获得大地高可求得正常高。这能够改变传统高程测量作业模式，以满足1∶1万、1∶5000甚至更大比例尺测图的迫切需要，加快数字中国、数字区域、数字城市等的建设，能够节约大量人力、物力，产生巨大的经济效益，因此具有特别重要的科学意义和社会效益。

2 GM（1，1）模型的建立

2．1 模型的建立

设某工程测区有n个GPS水准点，且各水准点的高程异常值已知，其相应的高程异常值序列为ζ（0）＝ （ζ（0）（1），ζ（0）（2），…，ζ（0）（n））；其一次累加生成序列为ζ（1）＝ （ζ（1）（1），ζ（1）（2），…，ζ（1）（n））。且满足

对式（2）在区间 ［ki，ki＋1］上积分，则有

令

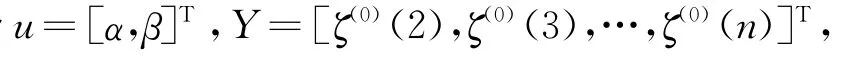
于是求解得

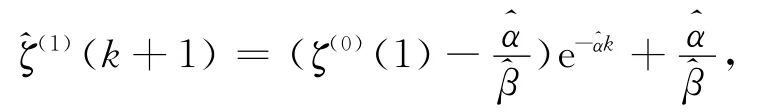
以上是通过高程异常值序列建立GM（1，1）模型的过程，建模过程显示，只需利用少量的GPS水准点就可以建立似大地水准面精化模型，并且可进行似大地水准面的变化趋势的预测。

2．2 GM（1，1）模型的预测步骤

2．2．1 已知建模数据的检验与处理

为了保证GM（1，1）模型建模的可行性，通常需要对高程异常值序列进行检验处理。设建模需用的高 程 异 常 值 序 列 为 ζ（0）＝ （ζ（0）（1），ζ（0）（2），…，ζ（0）（n）），计算序列的级比为

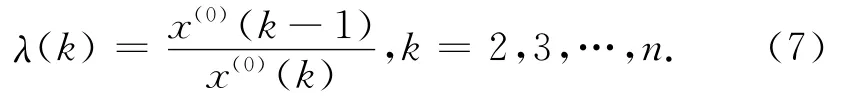
2．2．2 建立过程与计算流程

根据式（1）可建立基于GM（1，1）模型的似大地水准面精化模型，本文采用MATLAB语言编程对建模算法加以实现，其计算流程［7］如图1所示。

图1 基于MATLAB软件的建模算法流程

2．2．3 检验模型的预测值

对检验GM（1，1）模型的精度进行验证，可保证模型的可靠性，方便以后利用模型进行预报。通常可采用残差值级比偏差值进行检验。

令残差为ε（k），则

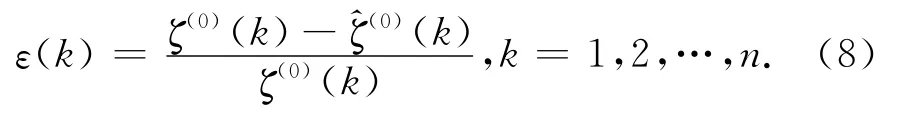
令级比偏差为ρ（k），则

通常认为，当ε（k），ρ（k）越小时，模型精度越高，达到的要求也越高。

2．2．4 GM（1，1）模型的预测预报

由GM（1，1）模型得到相应区域内的预测值，根据似大地水准面精化模型的实际需要进行预测，给出似大地水准面的变化趋势。

3 算例与分析

以云南省“兴地睦边”农田整治重大项目的某工程为例，测区均匀布设了10个GPS控制点，采用Tri mble天宝接收机施测了四等GPS控制网，利用其后处理软件进行基线处理，并在 WGS－84坐标系进行三维无约束网平差和在1980国家坐标系进行二维约束网平差，从而获得控制点的平面坐标（x，y）和大地高H。高程控制测量采用四等光电测距三角高程测量，并对高差进行加常数改正、乘常数改正、大气折光改正、地球曲率改正和温度改正，获得控制点的正常高h，由此得到了GPS控制点的三维坐标 （x，y，h），其成果见表1。

表1 测区GPS控制点的成果

根据GM（1，1）模型的建模及预测步骤，对工程测区的10个GPS控制点建立了似大地水准面精化模型，并对其精度进行验证。

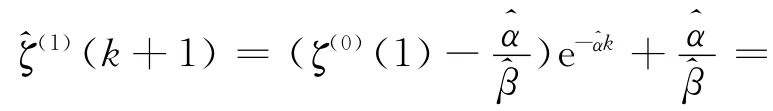
通过计算，得到GM（1，1）模型的各种计算及检验指标值的结果见表2。

表2 GM（1，1）模型的检验

由表2可知，利用GM 1 1模型建立的区域似大地水准面精化模型的残差、相对误差和级比偏差都很小，能够有效地反应似大地水准面的变化趋势，满足实际需求。

4 结束语

本文提出了一种利用灰色GM（1，1）模型来拟合高程异常值序列的方法，就其建模理论和计算流程进行了系统的介绍，采用MATLAB软件可靠的计算功能和强大的函数资源［5］对算法加以实现，并以某区域似大地水准面精化数据为例，验证了通过GM（1，1）模型建立区域似大地水准面精化模型的可行性。通过对模型的背景值进行重构，残差进行修正，扩展一些灰色模型的特性，可以提高建立似大地水准面模型的精度，进而更精确地预测似大地水准面的变化趋势，为工程建设提供更有力的保障。

［1］ 邓聚龙．灰理论基础［M］．武汉：华中科技大学出版社，2002．

［2］ 谢乃明，刘思峰．多变量离散灰色模型及其性质［J．系统工程理论与实践，2008（6）：143－144．

［3］ 戴文战，李俊峰．非等间距 GM（1，1）模型建模研究［J］．系统工程理论与实践，2005（9）：89－90．

［4］ 雷伟伟，张锋．区域似大地水准面精化模型算法的优选［J］．测绘工程，2011，20（1）：33－34．

［5］ 袁士涛．灰色理论在精化大地水准面中的应用［D］．成都：西南交通大学，2008：36－50．

［6］ 罗党，刘思峰，党耀国．灰色模型 GM（1，1）优化［J］．中国工程科学，2003，5（8）：50－52．

［7］ 王穗辉，潘国荣．基于MATLAB多变量灰色模型及其在变形预测中的应用［J］．土木工程学报，2005，38（5）：25－27．

［8］ 郭春喜，肖学年，王斌，等．GB／T 23709－2009区域似大地水准面精化基本技术规定［S］．北京：中国标准出版社，2009．

［9］ 徐绍铨，张华海，杨志强，等．GPS测量原理及应用［M］．武汉：武汉大学出版社，2008．

［10］司守奎，孙玺菁．数学建模算法与应用［M］．北京：国防工业出版社，2013．