一个包含Smarandache LCM对偶函数的方程
2015-03-27高丽马娅锋
高丽,马娅锋
(延安大学数学与计算机科学学院,陕西 延安 716000)
1 主要结论
对任意的正整数n,著名的Smarandache LCM函数的对偶函数定义为[1]:
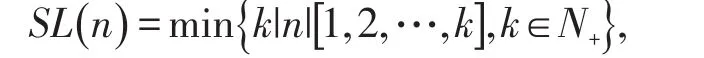
其对偶函数定义为[2-3]:
许多学者对SL∗(n)的算术性质进行了研究,获得了不少有趣的结果.例如,田呈亮[4]得到当n为奇数时;当n为偶数时.王妤[5]得到的正整数解.陈斌[6]得到了的正整数解.赵娜娜[7-8]得到了的正整数解.
本文中利用初等数论和分类讨论的方法研究方程

的正整数解,并得到其所有正整数解.
2 定理的证明
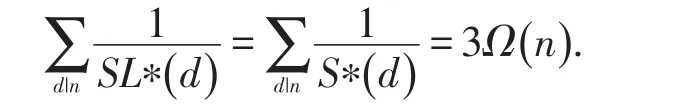
Ⅰ)当m=1时,n=2α,3Ω() n=3α,有
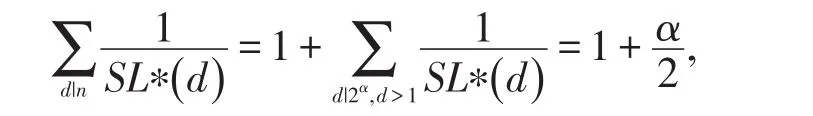
Ⅱ)当m>1时,分α=1和α>1两种情况,具体分析如下:
(ⅰ)当k=1时,n=2∙3α1,3Ω(n)=3(1 +α1),有
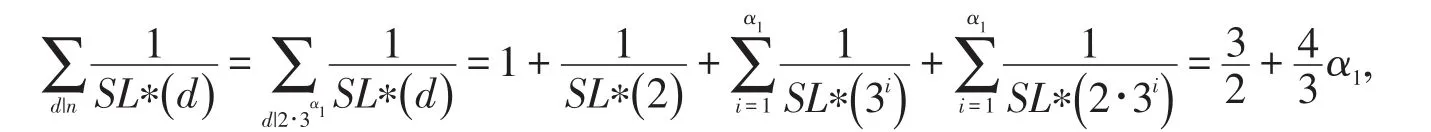
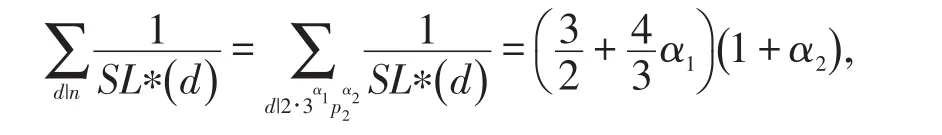


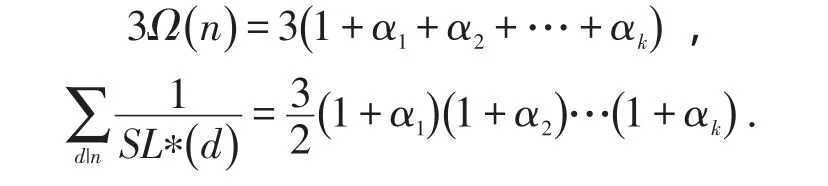
因此,方程(1)等价于
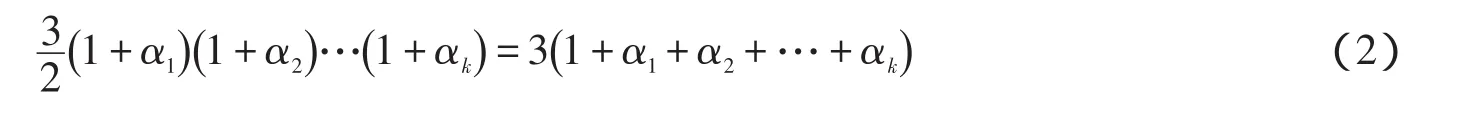
下面求解方程(2).
(ⅳ)当k≥4时,由数学归纳法证得,

易知此方程无正整数解,此时方程(1)无正整数解.
(Ⅰ)当3|m时,具体讨论如下:
(ⅰ)当k=1时,n=2α3α1,3Ω(n)=3(α +α1),有


为方程(1)的解.
①当p2=5时,即,有

因此,方程(1)等价于

可化简为6+3αα1+6αα2+10α2α1+2αα1α2=30α+27α1+30α2.由 java程序解得α=3,α1=2,α2=6;α=3,α1=4,α2=3;α=4,α1=6,α2=2;α=4,α1=40,α2=1;α=5,α1=3,α2=3;α=5,α1=18,α2=1;α=10,α1=18,α2=1;α=13,α1=2,α2=3;α=13,α1=7,α2=1;α=21,α1=6,α2=1;α=25,α1=3,α2=2;α=109,α1=5,α2=1.
②当p2>5时,有
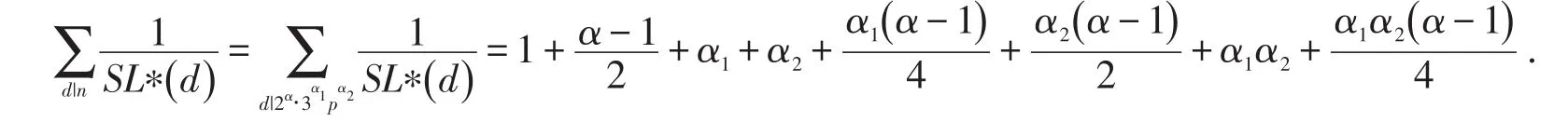
因此,方程(1)等价于
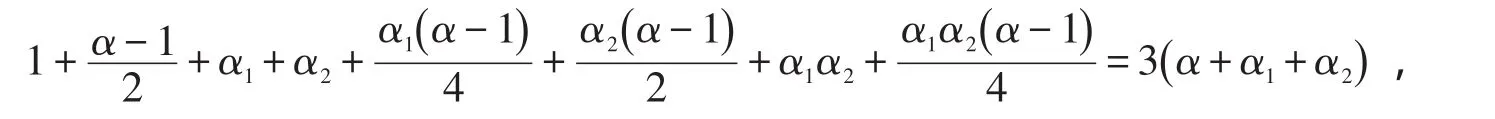
可化简为2+αα1+2αα2+3α2α1+αα1α2=10α+9α1+10α2.由java程序解得
α=2,α1=2,α2=8;α=2,α1=10,α2=2;α=3,α1=1,α2=17;α=3,α1=2,α2=5;α=3,α1=6,α2=2;α=4,α1=2,α2=4;α=4,α1=20,α2=1;α=5,α1=4,α2=2;α=5,α1=12,α2=1;α=7,α1=1,α2=5;α=7,α1=2,α2=3;α=7,α1=8,α2=1;α=9,α1=3,α2=2;α=11,α1=6,α2=1;α=19,α1=5,α2=1.即
①当p2=5,p3=7,α1=α2=α3=1时有

②当p2≠5,5<p2<p3,α1=α2=α3=1时
③当α1>1,α2>1,α3>1时,有

(ⅳ)因此,当k≥4时,方程(1)也无正整数解.
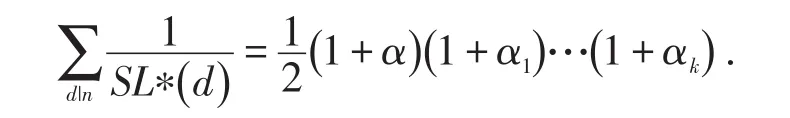
(ⅰ)当k=1时,方程(1)等价于1+αα1=5α+5α1,由java程序解得α=6,α1=29;α=7,α1=17;α=8,α1=13;α=9,α1=11;α=11,α1=9;α=13,α1=8;α=17,α1=7;α=29,α1=6.
α=2,α1=2,α2=5;α=2,α1=3,α2=3;α=2,α1=5,α2=2;α=3,α1=1,α2=8;α=3, α1=2,α2=3;α=3,α1=3,α2=2;α=3,α1=8,α2=1;α=4,α1=1,α2=5;α=4,α1=5,α2=1;α=5,α1=1,α2=4;α=5,α1=2,α2=2;α=5,α1=4,α2=1;α=8,α1=1,α2=3;α=8,α1=3, α2=1.即为(1)式的解.
解得α=2,α1=2,α2=1,α3=1;α=2,α1=1,α2=2,α3=1;α=2,α1=1,α2=1,α3=2.
因此,方程(1)无正整数解.
综上所述,定理得证.
[1]Smarandache F.Olny problems,not solutions[M].Chicago:Xiquan Publ House,1993.
[2]潘承洞,潘承彪.初等数论[M].北京:北京大学出版社,1992.
[3]张文鹏.初等数论[M].西安:陕西师范大学出版社,2007.
[4]Tian Chengliang.An equations involving the two Smarandache LCM dual function[J].Scientia Magna,2007,3(3):104-107.
[5]王妤.一个包含Smarandache LCM对偶函数的方程[J].黑龙江大学:自然科学学报,2008,25(5):645-647.
[6]陈斌.包含Smarandache对偶函数的方程的正整数解[J].天津师范大学学报:自然科学版.2012,32(3):6-8.
[7]赵娜娜.关于Smarandache LCM对偶函数方程的可解性[J].渭南师范学院学报,2013,28(9):14-18.
[8]赵娜娜.一个关于Smarandache LCM对偶函数的方程[J].纺织高校基础科学学报,2013,26(3):323-327.
[9]闫天国.关于Smarandache LCM对偶函数的一个方程[J].西南民族大学学报,2013,39(4):570-574.
[10]陈斌.一个包含Smarandache对偶函数的方程[J].西南大学学报:自然科学版,2012,34(12):92-96.
