考虑多级采动效应的边坡失稳过程研究

张拥军 陈关平 李乾龙 孙 涤 李 博 万 勇

(1.青岛理工大学土木工程学院，山东 青岛266033;2.中国科学院青岛生物能源与过程研究所，山东 青岛266101;3. 山东鸿顺集团，山东 济宁272000)

边坡稳定性是岩石工程研究领域内重要问题之一，在工程实践中，高边坡往往每隔一定高度设置一个平台，而传统的研究土质边坡稳定性的方法不能直接用于解决这种梯状边坡的稳定性分析［1-2］。研究边坡稳定性的传统方法主要建立在极限平衡理论方法基础之上，主要有极限平衡法、滑移线法、极限分析法等，而这些方法并没有考虑应力跟应变关系，无法分析边坡破坏的发生和发展。随着计算机技术发展，考虑了土体的本构关系及变形对应力影响的强度折减法的广泛应用，成为分析边坡稳定性强有力工具［3-4］。

连镇营［5］用强度折减有限元法对天然边坡和开挖边坡进行稳定性分析对比，得出具有相似的破坏形式，从而证明了强度折减法适用于开挖边坡的研究。韩爱民［6］引入FLAC3D程序和强度折减法理论对多级边坡随台阶的宽度变化进行研究，得出随着台阶宽度的减小边坡的稳定性减小，滑移面的位移、边坡的破坏模式及稳定性也随着台阶宽度的变化表现出不同的特征。陈佳［7］利用FLAC 软件对露天矿边坡的稳定性进行数值计算分析，得出边坡破坏在数值模拟中表现为计算的不收敛，塑性区的贯通只是边坡破坏的必要条件。陈国庆［8］为了真实再现边坡渐进失稳过程，提出了边坡渐进破坏的强度折减法，获得的位移变化趋势与破损区演化过程具有一致性。杨光华［9］在Duncan－Chang 非线性本构模型基础之上，建议在弹性阶段过程分析中对岩体的弹性模量也要进行折减，这样可以获得更符合实际的变形场。唐春安［10］、李连崇［11］对边坡的稳定性分析时将强度折减法引入到RFPA 中，不仅对滑动面不做任何假设而且还以基元的破坏次数统计作为失稳的判断准则，不仅直观地得到边坡体的滑移破坏面，而且还可以求得安全系数，在复杂环境地质下也是适用的。

通过强度折减法求边坡的安全系数，在多级边坡的稳定性分析中得到广泛应用，但是没有结合现场监测数据对边坡的局部破坏过程和破坏机理进行详细的阐述，造成多级边坡破坏过程和破坏机理关系不明确。而多级边坡局部破坏过程和破坏机理可以更合理地对局部稳定性进行定性分析，同时对多级边坡的监测预警也具有指导意义。

合理地选择分析方法和建模方式对多级边坡稳定性分析至关重要，以往很多数值模拟并没有真正意义上实现连续采动与强度折减结合，即在强度折减的过程中进行连续开采。本研究采用RFPA 有限元软件，在折减的过程中考虑连续采动的作用，研究多级边坡多次采动过程中局部化岩体损伤、破坏、失稳过程，再现多次采动影响下多级边坡局部失稳效应。实现真正意义上的强度折减和多级采动效应，使得破坏方式与实际开采过程更为接近，其损伤机理贴近实际情况。

1 研究背景

1.1 工程地质

以金川集团石英石露天矿多级台阶边坡为研究模型，目前许多区段边坡已产生不同程度的变形和破坏，主要表现:1 780 m 台阶中段出现局部坍塌;1 816 m 台阶西部出现许多裂缝，且不断扩大;1 792 m 台阶东部出现滚石。1 756 m 水平以下的1 744、1 732、1 720、1 708、1 696 m 等5 个水平将进入深凹采场。在采场北部边帮1 768、1 780、1 792、1 816、1 826 m 5个平台上拉网式布置21 个监测孔共84 个测斜仪(位置如图1 所示)。

1.2 研究模型

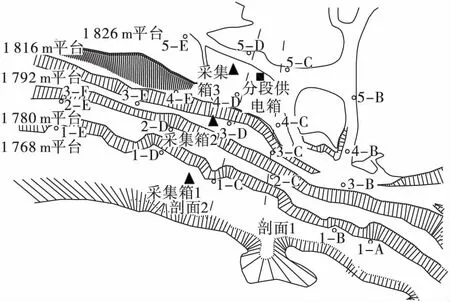
图1 监测孔位置分布图Fig.1 Location map of monitor holes

将现场多级边坡转换成平面应变问题，通过RFPA在细观尺度上建立本构模型，对现场非均匀岩性边坡进行数值模拟。以金川集团石英石露天矿勘察地质报告为设计依据，将图1 中剖面2 作为模拟对象，根据现场地质勘查报告，地层岩石参数见表1，建立如图2 连续采动多级边坡模型和如图3 一次开挖多级边坡模型。分别对2 个模型进行数值模拟并进行对比，分析随着强度折减的连续开挖和一次性开挖损伤机理和损伤过程的不同。

表1 地层岩石物理与力学参数Table 1 Physical and mechanical parameters of rock strata

图2 连续开挖多级边坡模型Fig.2 Continuous excavation model of multistage slope

图2 模型和图3 模型水平方向取150 m，垂直高度100 m，共5 类岩层，划分260 ×180 =46 800 个单元。边界条件:左右边界限制水平位移，竖向自由;底部限制水平与竖向位移。本模型只考虑自重，采用RFPA 强度折减法进行分析，强度折减系数0.01，加载步数80，最高迭代100 次。通过2 个模型1 768 m平台开采后卸载破坏情况，分析高陡边坡渐进失稳的过程损伤机理和损伤过程。

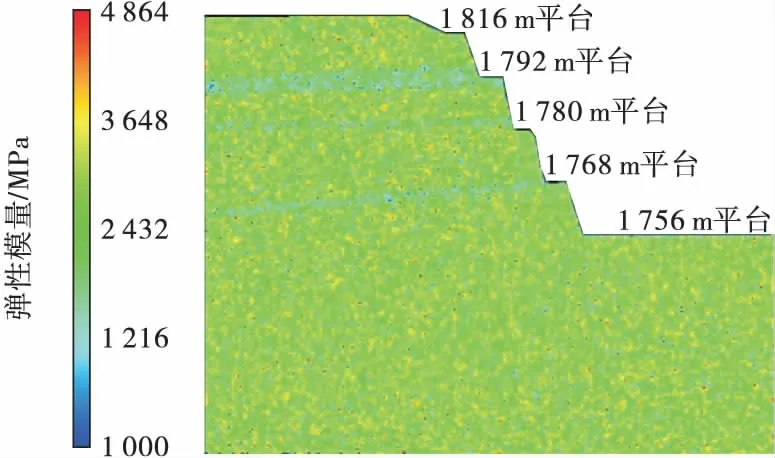
图3 一次开挖多级边坡模型Fig.3 Once excavation model of multistage slope

1.3 数值模型的参数选取分析

计算输入参数对原位模型数值计算模拟分析至关重要，RFPA 有限元软件进行模拟分析时，假设材料为非均质材料，材料细观力学特征的非均匀性服从Weibull 分布，并引入均质度系数m 控制材料的均匀程度，m 越小，岩石越不均匀，m 越大，岩石越均匀。通过均度系数m 将材料的细观力学特性与宏观力学特性建立起来，因此RFPA 中输入的细观均值可由实际物理力学参数的宏观值经过均度系数m 转化计算得到。RFPA 细观参数取值如下:

第一，根据实际地质情况及结构体几何尺寸大小，确定均质度系数m。

第二，根据拟合公式对输入的弹性模量和强度模量进行初步选取，计算式为［13］

式中，Eh和fh分别为数值试样的弹性模量和强度模量的宏观值;Ex和fx分别为Weibull 分布赋值时(数值计算输入值)弹性模量和强度模量的细观值。

由以上分析，将表1 中的宏观物理参数量代入式(1)和式(2)，由此可得到需要输入RFPA 中的细观均值。

2 数值模拟分析

2.1 连续采动卸荷数值分析

图4 是进行强度折减和连续开采结合模型的数值弹性模量图。图5 是对应的声发射图，图5 中浅黑表示当前步压剪破坏，深黑表示当前步拉破坏。声发射中圆圈的圆心代表声发射的位置，圆圈的半径代表声发射的能量。图4 和图5 由RFPA 有限元软件模拟得出。

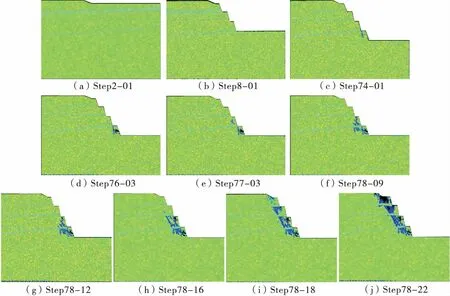
图4 连续开挖后弹性模量动态变化Fig.4 Continuous dynamic elastic modulus after excavation

图4 是通过数值模拟得出的1 768 m 平台开挖后高陡边坡的渐进失稳过程。随着强度折减到Step 76 －03 时，1 780 m 平台坡脚出现微损伤，当折减逐步增加，1 780 m 平台坡脚出现损伤且向1 768 m 平台坡脚扩展。1 780 m 平台坡脚损伤逐步积累并向1 768 m平台坡脚蔓延、贯通，与此同时1 768 m 平台坡脚损伤逐步向1 780 m 平台坡脚扩展，并偏向坡体内部方向，最终形成了损伤—积累—扩展—贯通的破坏过程，整个过程由原始损伤点诱导新的损伤向其扩 展，如Step77 －03 所示。与此同时，1780 m平台中上部出现局部损伤，且随着折减的过程进行，1 780 m 中上部损伤逐渐发展逐渐向1 780 m 平台坡脚扩展，贯通如Step 78 － 09 至Step 78 － 12。此时，1 780m 平台处及1 768 m 边坡中上部岩体出现局部破坏。

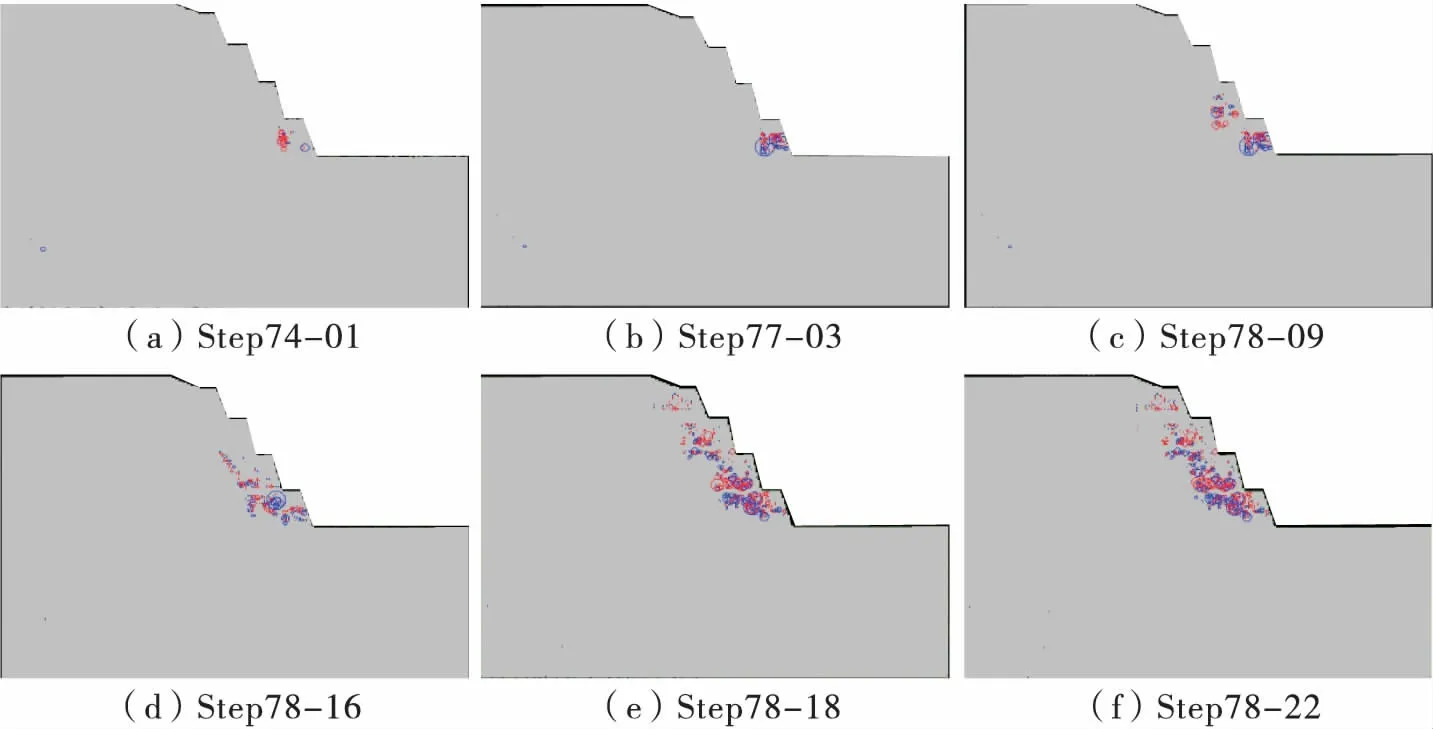
图5 声发射图Fig.5 Continuous dynamic elastic modulus after excavation

由图5 分析，当折减到Step 74 －01，1 768 m 边坡原离悬空面的内部岩体发生拉破坏，随着折减的进行，1 768 m 平台坡底出现压剪破坏，当折减进一步进行时，1 780 m 平台中上部岩体出现压减和受拉混合破坏，且在下部岩体发生贯通损伤之后1 780 m 平台出现损伤，由此分析，局部岩体破坏会引起岩体内部应力迁移。当折减到Step 78 －16，岩体内部损伤发展逐步加快，1 780 m 平台和1 768 m 平台损伤逐渐贯通，其后损伤逐渐加快，迅速扩展到1 792 m 平台和1 816 m 平台，上部岩体都是由1 816 m 平台坡脚及1 816 m 平台上部岩体突变截面处发生损伤，逐渐向岩体内部扩展，与下部损伤贯通。从整个破坏过程分析，多级边坡损伤主要产生局部损伤变化，如图5中Step78 －18，整个多级边坡并没有形成滑移带，只是局部发生破坏，但其损伤贯通整个多级边坡。由图5 可知，在整个损伤区域扩展蔓延的时候，其新的损伤区域呈现浅黑较多，由此可以判断损伤扩展主要发生压剪破坏。而损伤区损伤程度加大，其声发射区域主要呈深黑色，由此可以判断损伤区的损伤度加大，主要产生张拉破坏。

由以上多级边坡连续开采数值模拟分析，多级边坡的破坏过程是由开采1 780 m 平台坡脚发生起始损伤，并逐步向下部扩展，扩展过程中产生新的损伤点，形成贯通损伤区域，在整个扩展、贯通的过程中坡体局部发生应力迁移。随着强度折减，在新的应力分布环境下形成新的损伤点，新的损伤点进一步向已形成的贯通损伤区域扩展、贯通，再次形成新的损伤区域，随着损伤区域的增大其应力重分布影响的区域也将进一步扩大，进而引起新的损伤点，并由原始损伤区诱导新的损伤向其扩展、贯通。整个破坏过程可以归纳为起始损伤—新的损伤点—向已损伤区域扩展—新贯通损伤区域—新的损伤点，其中损伤的扩展、贯通伴随着岩体内部应力迁移。其次，高陡边坡起始损伤主要由张拉破坏造成，然后由剪切破坏引起损伤扩展。

从整个多级边坡失稳破坏过程分析，多级边坡顶部主要发生张拉破坏，坡面浅层主要发生拉张剪切破坏。坡面浅层张拉剪切破坏由坡脚向坡顶发展的过程中逐步向坡体内部偏移并转变成以张拉破坏为主，且多级边坡的中部台阶破坏较下部严重。

2.2 多级边坡的安全系数

在用RFPA 强度折减方法时，由折减系数μ 和失稳时当前的计算步求出未折减时结构的初始强度储备安全系数fs，fs的计算式如下［16］:

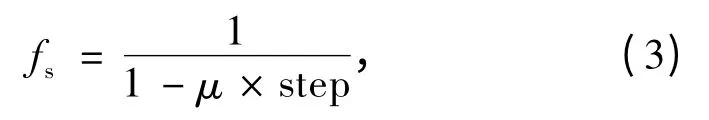
其中，step 为破坏时当前的计算步。

将上述模拟参数及结果代入式(3)，有

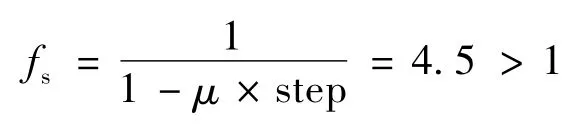
2.3 一次性开采卸荷数值分析

图6 是进行强度折减和一次性开采结合模型的数值弹性模量图，图7 是对应的声发射图。

图6 1 768 m 平台开挖后弹性模量动态变化Fig.6 1 768 m platform dynamic elastic modulus after the excavation

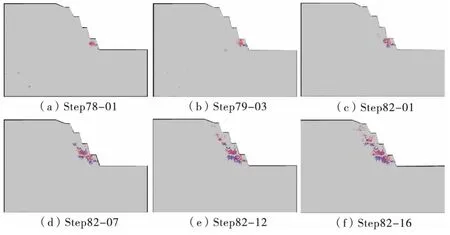
图7 1 768 m 平台开挖后声发射变化Fig.7 1 768 m acoustic emission after excavation

由以上一次开挖模拟过程分析，多级边坡损伤由边坡底部向上逐步发展，由1 768 m 平台坡脚附近出现起始损伤点，损伤点扩展、贯通形成损伤区域过程中，下部岩质边坡内部出现应力转移、应力重分布，1 780 m平台出现新的损伤点，已形成的损伤区域诱导新的损伤点向其扩展、贯通形成新的损伤区域。整个多级边坡损伤过程以此破坏过程为循环，每次损伤区域贯通之后，其影响岩体内部应力范围逐渐增大。一次性开挖并没有形成贯通的滑移带，只是局部产生损伤及破坏。

将上述模拟参数及结果代入式(3)，求得多级边坡安全系数为

fs= 5.6 ＞1.

2.4 连续开采和一次性开采分析结果对比

第一，连续开采最后求得的安全系数为4.5，一次开挖求得的安全系数为5.6。由此分析，一次开挖数值模拟的边坡安全系数偏大，算得的边坡安全贮备过于保守。

第二，连续开采和一次性开采损伤点都是由多级边坡局部损伤点开始萌生、扩展贯通，但是随着强度折减进行，连续开挖损伤区逐步向远离多级边坡悬空面扩展，一次性开挖损伤区沿着各平台坡脚逐步向上扩展。最终，连续开采1 792 m 平台和1 804 m 平台损伤度较大，一次开挖1 780 m 平台和1 792 m 平台损伤度较大，且1 792 m 平台坡脚损伤较严重。

由此可知，一次开采和连续开采只是在时间步骤、空间位置、多级边坡结构稳定性分析上不同，其损伤过程、损伤机理基本保持一致。损伤过程都是多级边坡坡脚发生起始损伤，起始损伤远离悬空面方向逐步向上扩展，且在每个坡脚内部附近岩体产生新的损伤点，原始损伤点诱导新的损伤点向其扩展，原始损伤和新的损伤点逐步逼近、重合、贯通。与此同时，伴随整个诱导贯通损伤的过程中，在该贯通损伤区上部继而产生新的损伤点，整个过程往复循环，逐步向多级边坡顶部发展。损伤机理，主要由剪切破坏引起损伤扩展，张拉破坏加大损伤度。多级边坡顶部主要发生张拉破坏，坡面浅层主要发生拉张剪切破坏。坡面浅层张拉剪切破坏由坡脚向坡顶发展的过程中逐步向坡体内部偏移并转变成以张拉破坏为主，且多级边坡的中部台阶破坏较下部严重。

3 监测数据分析

取对应数值模拟剖面2 上的现场监测数据，取剖面2 上3 个测点1 －C、3 －D、5 －D，将每个平台测点的位移场曲线与数值模拟的结果做对比，验证数值模拟分析结果的合理性。

3.1 1 －C 监测数据分析

取现场监测数据，2012-09-15—2012-10-15 期间3 m 测点发生较大位移，13 m、18 m 测点的位移差为负值，表示上部岩体位移向悬空面产生较大位移。

由图8 可以看出，1 －C(左侧为悬空面)测点8 m处向悬空面位移变形比较大，下部向悬空面逐步均匀增长，且位移变量较上部大。深度18 m 处测点的位移在2012-10—2013-04 期间底部位移增加97.6 mm，平均每个月位移增幅为16.3 mm。结合图4 Step 74－01、Step 76 －03 来看，1 768 m 平台坡体中上部破坏较下部发展较快，但是随着折减进行，1 768 m 平台坡脚损伤逐步发展如Step 77 －03 、Step 78 －09。1 －C 表面出现多条平行于悬空坡面的张拉裂缝，由图5中Step 74 －01 ～Step 78 －09 可以看出1 768 m 平台上部受张拉破坏。由以上分析看出现场多级边坡底部破坏形式与数值模拟基本保持一致。

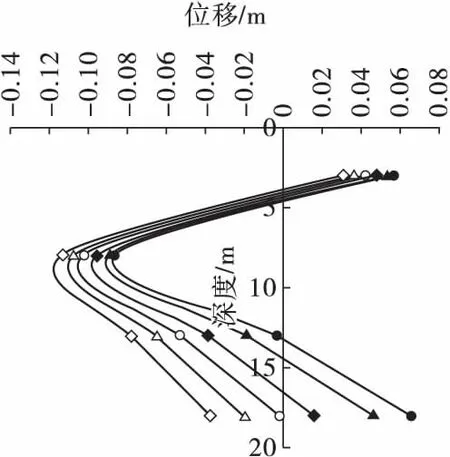
图8 1 －C 测点位移变化曲线Fig.8 1-C measuring point displacement curve

3.2 3 －D 监测数据分析

取现场监测数据，做位移变化图如图9。由图9可以看出，3－D 测点坡体中下部位移较大，且变化较明显。深度13 m 测点2013 －01—2013 －12 期间位移增大了31 mm，深度23 m 的测点在2013 －01—2013 －12 期间位移增大了30.2 mm。由图4 的Step78－16 可以看出1 792 m 平台坡脚损伤严重，并与1 780 m 平台形成了贯通，行成较大贯通损伤区域。深度在3 m 处的测点在2013 －01—2013 －12 期间位移增大了14.5 mm，由3－D 测点坡体表面破坏看出坡体平台表面形成了20 mm 宽度张拉裂缝，且裂缝方向平行于悬空面发展。由图5 中Step78－09 ～Step78 －18 可以看出，1 792 m 平台和1 780 m 平台坡体内部呈现拉张剪切破坏，坡体平台上部呈张拉破坏。由现场分析，剖面2 有自3－D 到1 －C 监测点的贯通型小规模滑带，且在1 792 m 平台3 －D 附近不断有新的裂缝产生。由以上现场监测数据分析可知，实际边坡破坏主要发生在坡体的下部，该破坏方式跟数值模拟破坏形式基本一致。

图9 3 －D 测点位移变化曲线Fig.9 3-D measuring displacement curve

3.3 5 －D 监测数据分析

取现场5 －D 监测数据做成曲线如图10。

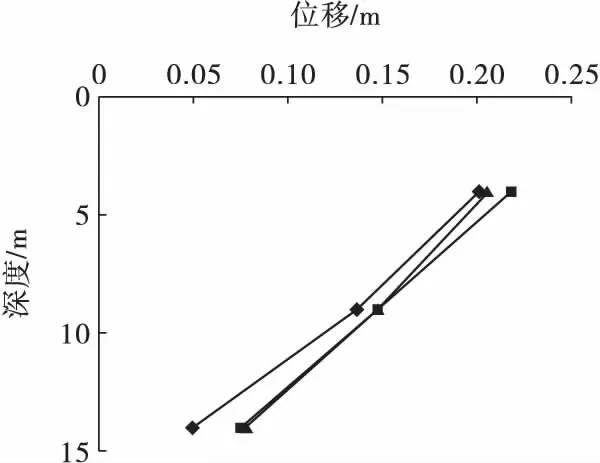
图10 5 －D 测点位移变化曲线Fig.10 5 －D measuring displacement curve

由图10 观察发现，5 －D(右侧为悬空面)测点上部坡体向悬空面倾覆，上部跟下部岩体变形差达到126 mm，深度3 m 处位移增大值达到16.6 mm。测孔4 m、9 m、14 m 测点在2012 －08 －04—2012 －08 －30 期间位移差逐渐减小由正逐渐变为负数，说明在此期间边坡先是由下部局部岩体发生破坏产生移动，且移动速率和幅度都较上部大，随着时间变化的过程中，上部局部岩体也逐渐发生移动，所以4 m、9 m 处的相对位移逐渐减小，其位移差也逐步减小变为负数，14 m 测点位移差在之后基本保持不变趋于稳定。由此分析上部位移主要是由于下部局部岩体发生破坏损伤造成上部岩体逐步失去平衡发生移动，当上部岩体位移变形量达到其极限抗拉强度时，便出现张拉裂缝。

在2012 －08—2013 －01 期间，深度14 m 测点位移增长量为31.3 mm。在多级边坡顶部局部出现张拉裂缝。由图5 中Step78 －16 ～Step78 －22 看出，多级边坡顶部出现大面积的损伤，该损伤区域主要产生张拉破坏。由此分析，5 －D 测点附近特征与模拟结果基本保持一致。

4 结 论

一次开采和连续开采只是在时间步骤、空间位置、多级边坡结构稳定性分析上不同，一次开采数值模拟的边坡安全系数偏大，得到的边坡安全贮备过于保守。时间、空间效应造成连续开采多级边坡局部破坏效应比一次性开采局部破坏效应明显。连续开采时间、空间效应对多级边坡每个坡脚附近产生起始损伤效应，而一次性开采起始损伤点由多级边坡底部向上逐渐循环诱导发展。在连续开采的过程中引起多级边坡局部失稳破坏。

连续开采和一次性开采多级边坡的损伤机理基本保持一致。连续开采下多级边坡在时间、空间效应作用下，由局部产生起始损伤点，起始损伤点逐步向靠近悬空偏向下方扩展形成新的损伤域。损伤域远离悬空面方向逐步向上扩展，且在每个坡脚内部附近岩体产生新的损伤点，原始损伤域诱导新的损伤点向其扩展，原始损伤和新的损伤点逐步逼近、重合、贯通。在伴随整个诱导贯通损伤的过程中，在该贯通损伤区上部继而产生新的损伤点，整个过程往复循环，逐步向多级边坡顶部发展。整个损伤破坏过程可以归纳为起始损伤—新的损伤点—向已损伤区域扩展—新贯通损伤区域—新的损伤点，其中损伤的扩展、贯通伴随着岩体内部应力迁移。

［1］ 时卫民，叶晓民，郑颖人. 阶梯形边坡的稳定性分析［J］. 岩石力学与工程学报，2002，21(5):698-701.

Shi Weimin，Ye Xiaomin，Zheng Yingren. Stability analysis on stepshaped slope［J］. Chinese Journal of Rock Mechanics and Engineering，2002，21(5):698-701.

［2］ 李 忠，朱彦鹏. 多阶边坡滑移面搜索模型及稳定性分析［J］.岩石力学与工程学报，2006，25(1):2842-2847.

Li Zhong，Zhu Yanpeng. Search model of slip surface and stability analysis of multi-step slope［J］. Chinese Journal of Rock Mechanics and Engineering，2006，25(1):2842-2847.

［3］ 郑颖人，赵尚毅. 有限元强度折减法在土坡与岩坡中的应用［J］.岩石力学与工程学报，2004，23(19):3381-3388.

Zheng Yingren，Zhao Shangyi. Application of strength reduction FEM in soil and rock slope［J］. Chinese Journal of Rock Mechanics and Engineering，2004，23(19):3381-3388.

［4］ 赵尚毅，郑颖人，时卫民，等. 用有限元强度折减法求边坡稳定安全系数［J］.岩土工程学报，2002，24(3):343-346.

Zhao Shangyi，Zheng Yingren，Shi Weimin，et al. Analysis on safety factor of slope by strength reduction FEM［J］. Chinese Journal of Geotechnical Engineering，2002，24(3):343 -346.

［5］ 连镇营，韩国城，孔宪京. 强度折减有限元法研究开挖边坡的稳定性［J］. 岩土工程学报，2001，23(4):407-411.

Lian Zhenying，Han Guocheng，Kong Xianjing. Stability analysis of excavation by strength reduction FEM［J］. Chinese Journal of Geotechnical Engineering，2001，23(4):407-411.

［6］ 韩爱民，李建国，傅国利，等. 基于有限差分强度折减法的多级边坡破坏模式研究［J］. 工程地质学报，2006，15(6):784-788.

Han Aimin，Li Jianguo，Fu Guoli，et al. Numerical analysis of falfure modes in slope with multi-steos using shear stenghen reduce on FDM［J］. Journal of Engineering Geology，2006，15(6):784-788.

［7］ 陈 佳，唐开元，周雪斐. 基于数值模拟的露天边坡强度折减法稳定性分析［J］. 金属矿山，2012(6):26-28.

Chen Jia，Tang Kaiyuan，Zhou Xuefei. Analysis the stability of slope in open-pit mine by strength reduction methods based on numerical simulation［J］. Metal Mine，2012(6):26-28.

［8］ 陈国庆，黄润秋，石豫川，等. 基于动态和整体强度折减法的边坡稳定性分析［J］. 岩石力学与工程学报，2014，33(2):243-256.

Chen Guoqing，Huang Runqiu，Shi Yuchuan，et al. Stability analysis of slope based on dynamic and whole stenggth reduction methods［J］. Chinese Journal of Rock Mechanics and Engineering，2014，33(2):243-256.

［9］ 杨光华，张玉成，张有祥. 变模量弹塑性强度折减法及其在边坡稳定分析中的应用［J］. 岩石力学与工程学报，2009，28(7):1506-1512.

Yang Guanghua，Zhang Yucheng，Zhang Youxiang. Variable modulus elastic-plastic strength reduction method and its application to slope stability analysis［J］. Chinese Journal of Rock Mechanics and Engineering，2009，28(7):1506-1512.

［10］ 唐春安，李连崇，李常文，等. 岩石工程稳定性分析RFPA 强度折减法［J］. 岩石力学与工程学报，2006，25(8):1522-1530 .

Tang Chun＇an，Li Lianchong，Li Changwen，et al. RFPA strength reduction method for analysis of stability of rock engineering［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25(8).1522-1530 .

［11］ 李连崇，唐春安，梁正召，等. RFPA 边坡稳定性分析方法及应用［J］. 应用基础与工程科学学报，2007，15(4):501-508.

Li Lianchong，Tang Chun＇an，Liang Zhengzhao，et al. RFPA method for slope stability analysis and associated application［J］. Journal of Basic Science and Engineering，2007，15(4):501-508.

［12］ 张拥军，杨登峰，王金涛，等. 露天边坡局部失稳特征的数值分析及检测［J］. 金属矿山，2014(10):142-147.

Zhang Yongjun，Yang Dengfeng，Wang Jintao，et al. Numerical analysis and monitoring of local instability characteristics of the open pit slope［J］. Metal Mine，2014(10):142-147.

［13］ 朱万成. 混凝土断裂过程的细观数值模型及应用［D］. 沈阳:东北大学，2001.

Zhu Wancheng.Mesoscopic Numerical Model for Fracure Pocess of Concrete and Its Application［D］.Shenyang:Northeastern University，2001.