一种节流流量传感器测量滞后的校正方法*
2015-03-26邓罗泉王立国郑铁军刘卓巍胡金海
邓罗泉,王立国,郑铁军,刘卓巍,程 礼,胡金海
(空军工程大学 航空航天工程学院,陕西 西安710038)
0 引 言
节流流量传感器广泛用于石油、化工、航空、冶金、供水、造纸等行业。在流量突变的情况下,节流流量传感器很容易发生测量滞后,而节流流量传感器是流量控制系统的重要组成部分,其发生测量滞后对流量控制系统的稳定性影响很大,因此,解决流量传感器的滞后问题对工程中的精确控制很有意义。
为了解决传感器的滞后问题,国内外学者做了大量的研究工作,并且取得了不少成果。文献[1 ~4]都采用GM(1,1)预测模型来解决传感器的滞后问题,但这种方法还没有在流量传感器上应用。杨英等人[5]则通过改进传感器的结构来消除传感器的惯性。
当流量变化较大时,现有的流量测量方法不能满足测量精度[6,7]。目前,国内外还没有针对节流流量传感器的测量滞后问题的解决方案,很有必要研究一种实用的方法来解决这个问题。为此,本文在GM(1,1)预测模型的基础上,提出了一种采用自适应加权的新陈代谢校正方法,并用实验验证了该方法的可行性和有效性。
1 系统建模
1.1 节流流量传感器
节流流量传感器主要由节流件、取压装置、测量管、导压管、法兰盘等组成,如图1 所示。
节流流量传感器的工作原理为:流体流经管道内的节流件时,将会在节流件处形成局部收缩,从而使流速增加、静压力降低,这时在节流件前后产生了静压力差。当工况一定时,根据流动连续性原理和伯努利方程,可以推导出管道流量与静压力差的关系如下
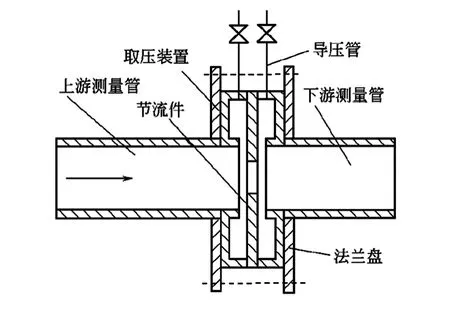
图1 节流流量传感器的组成Fig 1 Composition of throttle flow sensor

式中 qV为体积流量,C 为流出系数,A0为节流孔面积,β为节流装置的直径比,ε 为膨胀修正系数,ρ 为流体的密度。当测得静压力差Δp 时,就可以通过式(1)计算出流量。
1.2 自适应加权
由于节流流量计新测得的数据比老数据包含更多的能预测下一个流量值的信息,因此,要采用自适应滤波法给予新测得的数据更大的权重。其实施办法是:首先对所有测量数据进行归一化处理,然后取出测量数据的前一部分,给它们指定一组权重值,接下来预测测量数据的后一部分,将预测值与实际测量值进行比较,求出预测误差,最后再根据预测误差来调整相应的权重值。如此反复进行,直到预测误差小于0.01 为止。
自适应滤波法的预测公式如下
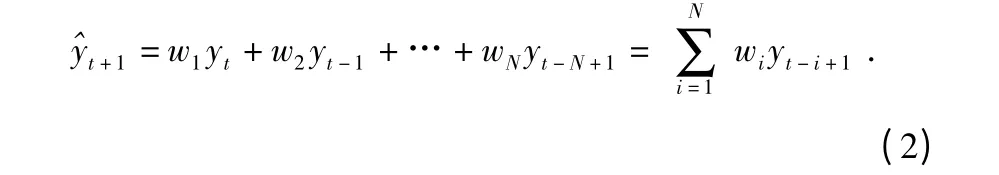
权重值用下式调整

式中 wi为调整前的第i 个权数,w'i为调整后的第i 个权重值,k 为自适应常数,ei+1为第t+1 个数据的预测误差。本次测得的数据序列无明显的周期变动,可以采用自相关系数法来确定N,即N 取最高自相关系数的滞后时间值,本文N 取4。依据文献[7],自适应常数和初始权重值都取1/N。
对测量数据给定权重值后,需要基于这些测量数据建立GM(1,1)流量预测模型。
1.3 GM(1,1)预测模型
设已经记录下来的n 个流量值序列:X(0)=[x(0)(1),x(0)(2),…,x(0)(n)],建立流量值预测公式

其中,a,b 分别为发展系数和灰色作用量。
1.4 模型优化
1.4.1 建立残差GM(1,1)模型
用残差序列^ε(0)修正预测值 ^X(0),建立残差修正GM(1,1)模型
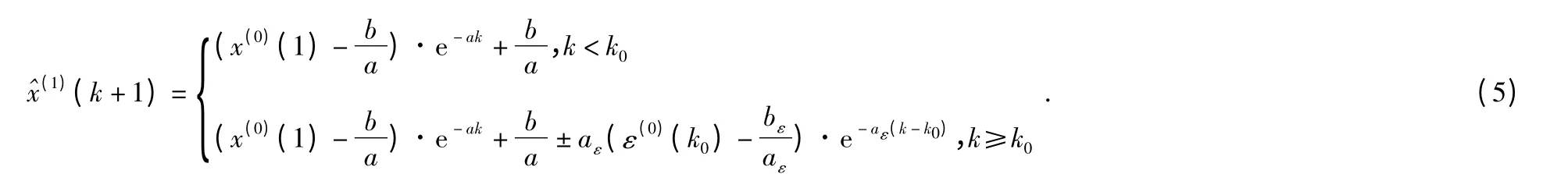
1.4.2 新陈代谢GM(1,1)模型
为了使预测效果达到最佳,必须不断去除老数据并加入新数据,这样使得建模序列能够更好地反映出系统的实时特征。于是采用以下方法:在流量值序列中,先删除最开始测得的流量值,再加入最近测得的流量值x(0)(n+1),建立新陈代谢GM(1,1)模型X(0)=(x(0)(2),x(0)(3),…,x(0)(n+1))。
1.5 模型的工作流程
模型的工作流程如图2 所示。
2 实验结果分析
本次实验首先将LGBH—0803C 节流流量传感器、带有校正装置的LGBH—0803C 节流流量传感器和ZRN—100 超声波流量传感器放置在同一管道内,然后在管道内迅速通以100 m3/h 的水流,并实时记录传感器显示的数据,最后将记录的数据归一化处理,用Matlab 软件对处理后的数据进行数据拟合并画出图像。超声波流量传感器的惯性极小,可以认为它所测得的流量值就是实际通过管道的流量值。本文先采用GM(1,1)预测模型来校正测量数据,结果如图3 所示。
由图3 可知,当t=0.4 s 时,实际通过管道的流量达到稳态流量的88.4%,节流流量传感器显示的流量值却只是稳态流量的35.1%,由此可见节流流量传感器具有很大的惯性。当t=0.5 s 时,实际通过管道的流量是稳态流量的94.3%,没有经过校正的传感器显示的流量值是稳态流量值的39.6%,而经过GM(1,1)预测模型校正过的传感器显示的流量值是稳态流量的92.7%,可见GM(1,1)预测模型很好地消除了传感器的惯性。但当流量趋于平稳时,GM(1,1)模型预测的数值却一直小幅度地增加,这是因为GM(1,1)模型所表征的时间序列是呈指数规律变化。由于残差GM(1,1)模型能很好地消除这种现象,为此,采用残差GM(1,1)模型对GM(1,1)模型进行修正,修正结果如图4 所示。
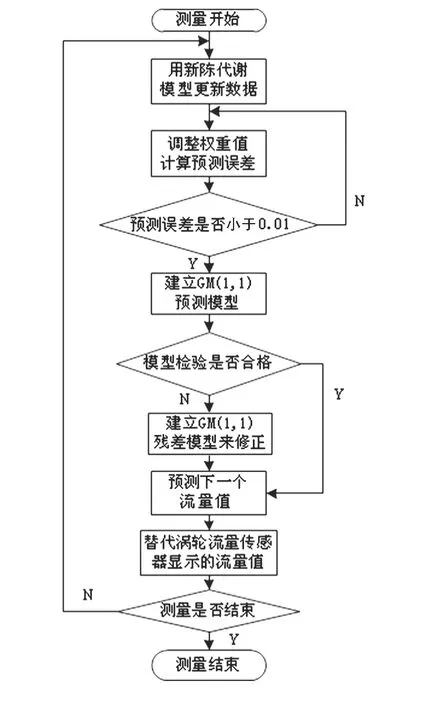
图2 模型的工作流程Fig 2 Workflow of model
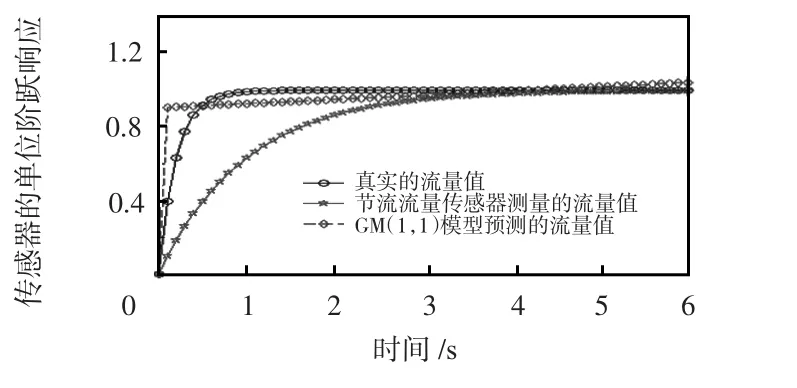
图3 GM(1,1)模型校正效果Fig 3 Correction effect of GM(1,1)model
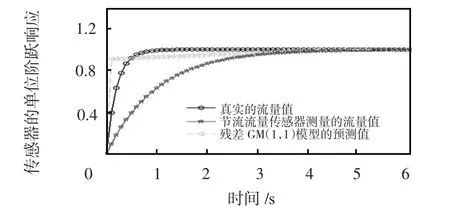
图4 残差修正后模型的预测效果Fig 4 Prediction effect of model after residual correction
由图3 可以看出,当t=6 s 时,用GM(1,1)模型预测的流量值为稳态流量值的102.6%,而且随着时间的增大,它预测的流量值会越来越大,相应的预测误差也会越来越大。而从图4 可知:经过残差修正后的GM(1,1)模型t=6 s 预测的流量值与实际通过管道的流量值基本相等,由此可以看出残差修正能够减少GM(1,1)模型4.1s 后的误差。但从图3 和图4 可以看出,在0~0.5 s 期间,GM(1,1)模型和经过残差修正后的GM(1,1)模型的预测值都远大于真实流量值,于是采用自适应滤波法来解决这个问题,结果如图5所示。
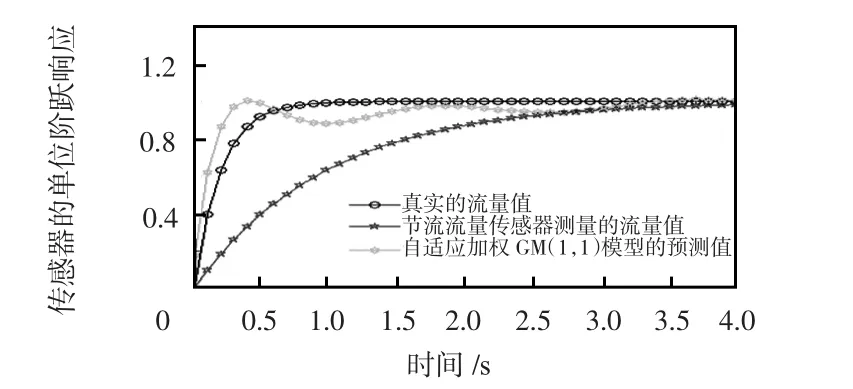
图5 自适应加权后模型的预测效果Fig 5 Prediction effect of adaptive weighted model
由图5 可知,在0.1,0.2 s 时,实际通过管道的流量分别为稳态流量的39.8%,64.1%,GM(1,1)模型的预测值分别为稳态流量的91.2%,92.4%,远大于真实的流量值。采用自适应滤波法后,在0.1,0.2 s 时的预测值分别为稳态流量的62.2%,88.5%,一定程度上提高了精度。但此模型预测的流量值出现了明显的波动,这是因为自适应常数k 取得过大,导致权重值调整过大,最后就引起了模型预测的流量值发生了波动。所以,要减少k 的取值,依据文献[8]重新对k 取值

此外,为了实现对流量的实时预测,采用新陈代谢模型不断更新数据,进一步提高测量精度。减少k 值和采用新陈代谢模型后预测的效果如图6 所示。
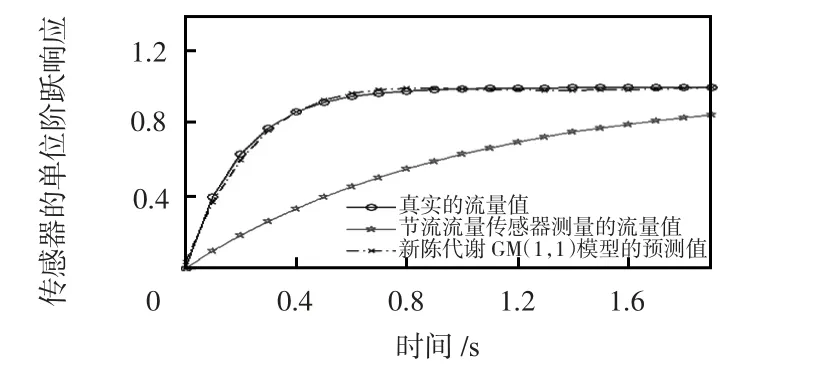
图6 减少k 和采用新陈代谢模型的预测效果Fig 6 Prediction effect of reducing k and using metabolic model
由图6 可知,减少k 的取值和采用新陈代谢模型取得的效果非常显著,在流量测量的前1.8 s,模型预测的流量值与实际通过管道的流量值的相对误差在0.5%以内,当测量时间大于1.8 s 后,模型预测的流量值与实际通过管道的流量值几乎完全相等,这说明所建立的模型的精度非常高。
实际测量和四种校正方法的误差如图7 所示。实际测量和四种校正方法的平均相对误差如表1 所示。
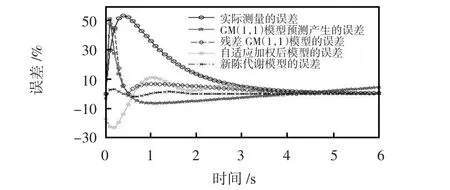
图7 实际测量和四种校正方法的误差Fig 7 Error of actual measurement and four types of correction methods

表1 平均相对误差Tab 1 Average relative error
由图7 和表1 知,以上的四种改进方法都提高了测量精度,尤其以新陈代谢模型最为有效,它能够将平均相对误差控制在0.38%以内,大大提高了原有测量方法的精度。
3 结 论
1)没有经过校正的节流流量计的平均相对误差为15.7%,采用本文所提方法校正后的平均相对误差为0.38%,可见本文所提方法取得了较好的效果。
2)自适应常数k 是自适应滤波法中的一个重要参数,k取得过大会导致预测的流量值出现波动。
3)对GM(1,1)模型进行残差修正和采用新陈代谢模型可以显著提高精度。
[1] 李顶根,汤 灿.VVA 汽油机进气道燃油观测器的研究[J].内燃机学报,2010,28(6):564-568.
[2] 吴义虎,侯志祥,刘 晖.电喷汽油机过渡工况进气流速的灰色GM(1,1)预测研究[J].内燃机工程,2006,27(2):33-35.
[3] Khuman A S,Yang Yingjie,John R.A new approach to improve the overall accuracy and the filter value accuracy of the GM(1,1)new-information and GM(1,1)metabolic models[C]∥IEEE International Conference on Systems,Man,and Cybernetics,IEEE,2013:1282-1287.
[4] Jia Zhengyuan,Li Wei,Han Zhuhua.An improved GM(1,1)-genetic algorithm to short-term forecasting in power system[C]∥4th International Conference on Wireless Communications,Networking and Mobile Computing,WiCOM 2008,2008:12-14.
[5] 杨 英,陈向东,蔡 镔.传感器薄膜结构的改进与响应时间的分析[J].传感器与微系统,2009,28(5):52-54.
[6] Amit Kumar Pandey.Low cost sensor for low flow rate measurement[C]∥Sensors for Industry Conference,Houston,Texas:The Instrumentation,Systems and Automation Society,2005:6-8.
[7] 董文永,刘 进,丁建立,等.最优化技术与数学建模[M].北京:清华大学出版社,2010:281-295.
