深孔法技术在铝合金构件应力场测试中的应用

廖 凯，刘义鹏，常星宇，赵 青

(中南林业科技大学 机电工程学院，长沙 410004)

目前，能够应用在高强铝合金厚板及薄壁构件的应力测试方法，主要包括：第一类是基于表面应力且无损的X射线衍射技术和钻孔法，适用于大多数金属材料的表面应力测试；第二类是基于深度应力且有损的层削法和裂纹柔度法[1-2]，这些方法只适合于规则板材，对于复杂构件不行；第三类是高端的无损深度应力测试，代表是中子衍射技术，但目前国内还不具备检测条件，国外这类设备的使用也非常昂贵和费时[3-4]。因此，探讨一种可以简单实现且准确性较高的力学深度应力实验测试方法，是目前国内外学者们研究深度应力测试的主要方向。深孔法测试技术(DHD)是目前国际上用于深度应力测试的主要方法之一，其兼顾了第一类和第二类测试方法的优点，是一种能够测量部件内部残余应力的半破坏性微损测量方法，其从表面钻孔法(ASTM 标准)发展而来，特别适用于一些复杂构件材料，同时，由于其破坏性较小，在一些焊接件和大型结构件、复合件上应用日趋广泛。

这一方法是学者最初为解决岩石内部应力状况而提出，工程师们试图用钻孔的方法探知岩石内部应力，并相继在这个方面做了深入研究，后来逐渐过渡到金属材料，主要应用于黑金属、焊接构件应力测试领域。TIMOSHENKO等[5]首次描述了深孔法测试材料内部残余应力的原理和可能，后来经过 GRANADAGARCIA 等[6]、GOUDAR 等[7]和 HOSSEINZADEH等[8]修正得到目前在应用的计算模型，随后其应用领域被扩展，焊接件和复合材料等应力测试开始引入这一技术。深孔法技术目前仍在不断发展和完善，国外在这方面的实验研究对象大多是黑金属和焊接件，而有色金属由于其内部应力强度普遍低于前者的，在深孔法小孔变形测量问题上增加了难度，因此，该方法的测试准确度还有待进一步提高。MAHMOUDI等[9-10]使用深孔法技术测量了环形焊接圆盘的非轴对称应力，BATEMAN 等[11]、DEWALD 等[12]和 KINGSTON[13]对复合材料进行相关应力测试研究，并与中子衍射作了对比，随后在已有深孔法技术基础上作了改进，使得测量残余应力的精度提高。SKOURAS等[14]和GOUDAR[15]运用有限元仿真分析该技术的精度问题，研究确定深孔法选择的环切直径关系与深孔法技术精确度之间的关系。目前普遍认为深孔法测试有两个特点需要关注：一是当环切直径增大时深孔法的误差会随之增大；另一是深孔法的最大误差出现在最大应力处[16]，尤其是表面。现在国内相关的研究文献很少，张炯等[17]采用三点弯曲试验预制钢件残余应力，研究深孔法残余应力测试技术，通过对比理论残余应力和实测残余应力验证了测试方法的准确性，但是在靠近试样表面处由于测量设备的限制及孔的边缘效应会产生一定误差。

本文作者研究分析深孔法对铝合金材料内部残余应力的测试技术，通过深孔法机理分析和有限元计算对比，对原有数学模型在应力表面-深度分布上的差异进行分析和修正，完善深孔法在有色金属应力测试领域的应用。

1 测试方法与力学模型

1.1 测试方法

深孔法测试思想起源于钻孔法，都是利用小孔周围应力释放后的应变来间接获取小孔处应力强度的微损方法。该法测量原理是测量实验小孔产生的变形，通过测定小孔内径的变化来反求该处残余应力，因此，其测得的应力值有两个特征：一是场特征，即测得的应力可以对孔深的各个方向应力进行求解描述；另一个则是局部特征，即测得的应力只代表孔的周围应力强度，如果在一块大型板件上分布着不均匀应力，则需要在不同的位置进行深孔实测。

测试方法：首先在材料待测处钻直径很小的通孔，通孔直径在3 mm以内，然后再以该孔为中心，将孔周围(半径小于5 mm)材料按照一定直径一并环切，环切采用电火花加工，以避免外场加工应力对测试的影响，逐层环切，每一次层深进给尽可能小，待应力释放后测量小孔内径的变形。该测试方法的难点在于如何精确的测量小孔深度方向垂直平面上不同角度的直径变化，测试精度1 μm。实验步骤如图1所示[14]。

深孔法实验包括 4个步骤：1) 在待测点做上标记，预打孔部位上下表面都贴上衬块。将贴好衬块的板安装到枪钻系统上，用枪钻在预打孔处钻孔径为 3 mm通孔；2) 测量上一步中所钻小孔在深度方向上小孔直径，作为小孔初始参考直径。在深度Z上规定X和Y轴方向，以X轴正方向为0°，顺时针方向为正，同一截面记录至少3组以上角度与其对应直径数据，记录并保存数据；3) 将测量后的铝合金厚板安装到电火花加工机床上，对所钻通孔进行对心定位。刀具为直径10 mm，对预加工处进行环切，相比于铣削加工而采用电火花加工，主要是为了减少加工应力对测试应力的影响；4) 测量电火花加工后小孔的变形，作为小孔变形后直径，测量要求与步骤2)一致，逐层环切，直到切通试件。

1.2 模型分析

实验步骤2)和4)中所测量的直径数据都与某一深度平面上的角度一一对应，即在同一深度平面上按照0°、45°、90°或任意角度得到 θ0°、θ45°、θ90°等角度处的小孔直径，实验中深度步进距离一般为0.2 mm，但在模拟中可以根据单元厚度2 mm来测试直径变化(因为生死单元本身忽略了加工应力的影响)。规定在步骤2中所测的小孔直径为dθ，而在步骤4)中所测得的小孔直径为d′θ。

定义小孔加工前后的变形为 Δdθ=dθ-d′θ。由测量的小孔某一个深度方向上的变形计算厚板同一深度方向上应力的数学模型表达式[16]为

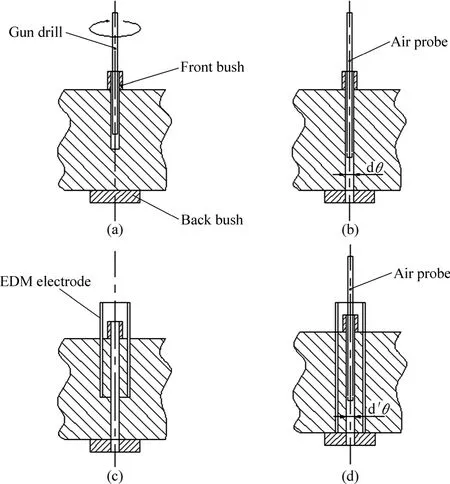
图1 深孔法实验过程Fig. 1 Experiment process of DHD: (a) Step 1; (b) Step 2; (c) Step 3; (d) Step 4

式中：()ε θ为小孔应变；E为弹性模量；xσ为在同一深度平面上X方向的应力；yσ为在同一深度平面上Y方向的应力；xyσ为在同一深度平面上X、Y方向的应力。

在一个深度方向上测量了多个角度的直径变形大小时，式(5)可表示为

从式(6)可看出，只要获知小孔内壁任意深度上在不同角度上的变形量，就可以求取该深度上各个方向上的应变，通过材料本构关系式(7)再求得这一深度上的应力强度 σ。从数学模型上看，任意角度分布的应力都可以计算，但模型可能会遇到一些问题：1) 模型对材料表面应力的求解精度会受到表面组织不均匀性影响，从而造成比较大的计算误差，说明深孔法在评价表面应力(应力峰值通常很大)时存在不足，要解决这一点，需要对模型的计算效果进行偏差归纳。2) 数学模型中只考虑了层深上不同角度的变形，从而计算应力的大小，但是，这取决于变形的完全释放，而变形是否完全释放，与材料尺寸和夹持约束对小孔的变形有关，这些都影响着计算的准确性。因此，本文作者通过有限元分析计算与模型本身计算来进行对比，就深孔法应力计算模型进行针对性的修正和改进，使得在材料深度应力中保持较高的准确性。

2 有限元模拟仿真

2.1 建模

本文作者以7075铝合金淬火圆棒为研究对象，针对深孔法测试实验步骤以 Mac.Marc有限元软件进行模拟仿真。试样淬火后，在中间均匀区进行深孔环切仿真，试样尺寸分别选为 d 80 mm×40 mm，d 100 mm×50 mm，d 120 mm×60 mm。图2所示为仿真模型尺寸，图3所示为有限元模型。模型采用8节点6面体单元全尺寸，温度场单元类型43号单元，应力场为7号单元，单元厚度2 mm。淬火方式为固溶加热至475 ℃并保温2 h，然后用20 ℃的淬火介质水冷却。

淬火热应力以热-力准耦合计算方法获得，仿真步骤为先对圆棒模型进行温度场及应力场的计算，再进行环切仿真。试件温度场初始温度475 ℃，环境温度为20 ℃，换热系数为8.5，约束模型上下两个表面。温度场计算结果作为其应力场模型的初始条件，将 X坐标为0的平面上所有节点添加X方向的位移约束，Y方向与Z方向的位移约束也是约束相应坐标为0平面上的所有节点。最后，将应力计算的结果文件作为初始条件施加到运用生死单元技术环切的仿真计算中，以使得深孔法测试的对象保留为原始应力分布状态。最后采用生死单元技术，模拟电火花环切加工中材料的去除过程。

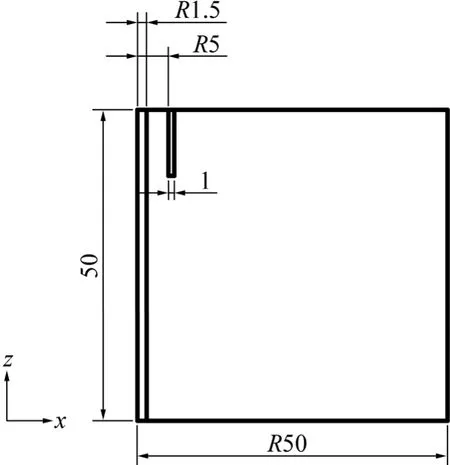
图2 试样实验尺寸Fig. 2 Sample size of DHD (Unit: mm)

图3 试件三维模型和环切示意图Fig. 3 3D model (a) and ring cutting (b) of sample FEM

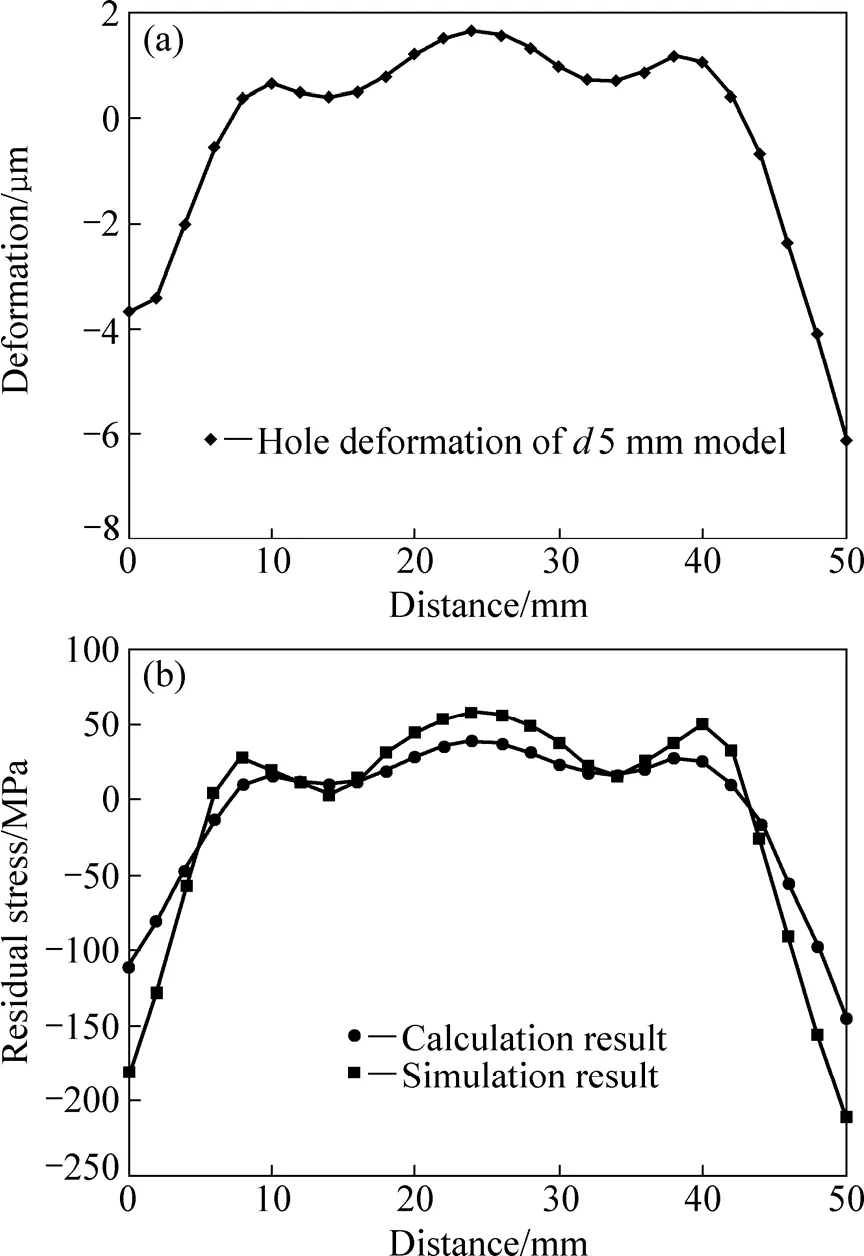
图4 d 50 mm试样应变-应力图Fig. 4 Stress-strain distribution of d 50 mm sample: (a)Strain distribution of small through hole; (b) Stress contrast of calculation and simulation

2.2 计算模型改进

根据上述实验和建模方法，运用生死单元技术将小孔周边材料进行环切去除，随后，读取小孔孔径沿深度上的变形，如图 4(a)所示。由于对试样的底部做一定的约束，使得热应力沿深度分布具有一定的不对称性，这样更有利于验证计算模型的准确性。根据深孔法应力计算的数学模型，将得到的孔径变形数据代入式(1)和(5)～(7)，模型计算后的应力分布如图4(b)所示，由此可见，表面应力为最大应力。

由图4(b)可以发现，两者计算结果存在偏差，计算应力比实际应力分布整体偏小，尤其是夹持部位的表面应力，偏差最大。导致的原因主要由于约束面导致了该层表面应力释放受到影响，而致使表面应力发生了突变，这个变化显然与铝合金棒热应力物理变化规律不吻合。虽然应力分布存在偏差，但两者应力分布曲线近似，是否由于材料尺寸对深孔变形产生了一定的影响，在计算中要考虑尺寸对计算的影响，尤其是厚度H的影响。针对上述原因，对应力曲线进行分析后认为，如果要进行计算模型的修正，可以运用比例系数修正和表面拟合化修正相结合的方法。针对上述问题，对现有深孔法应力计算模型进行改进。

1) 对表面变形的拟合处理：遵循淬火物理变化过程的变形协调性，对表面变形产生的偏差，所以可由已知的深度应变，推导表面处应变值，并进行对比分析检验处理效果。已知 ε1(θ)、ε2(θ)、ε3(θ)代表第二层、第三层、第四层环切后节点处读取的变形，可以构造一个表层变形分布曲线的拟合函数，如图4所示可知用一个二次函数已可满足精度。

将已知变形代入式(8)，即可求出x=0时，表面的修正变形ε1。式中c为待定系数，可以直接求解。

2) 对计算数据修正，考虑到厚度对数据的影响，初拟比例系数：

式中：e为自然常数，H为试件厚度数值，无量纲。即联立式(7)和(9)可得

深孔法计算应力由式(8)和式(10)求得。为验证其改进修正后的计算模型准确性和适用性，对直径为40 mm和60 mm的圆棒进行仿真模拟，在应力场计算上对两者的计算结果进行对比。

2.3 应用与分析

运用改进后的深孔法计算模型，对50 mm的铝合金淬火圆棒料模型进行了内应力场的重新计算分布，如图5所示。改进后的计算曲线与模拟的计算曲线已经非常接近，吻合度较高，平均偏差小于20 MPa，说明改进后深孔法计算模型能够较好地反映实际应力分布强度。

为了进一步论证该模型的适用性，取不同尺寸圆棒试样d 80 mm×40 mm，d120 mm×60 mm进行了相似的计算验证，结果如图6所示。

图5 d 50 mm样品模型改进算法后应力分布对比Fig. 5 Stress contrast using improved calculated model in d 50 mm sample

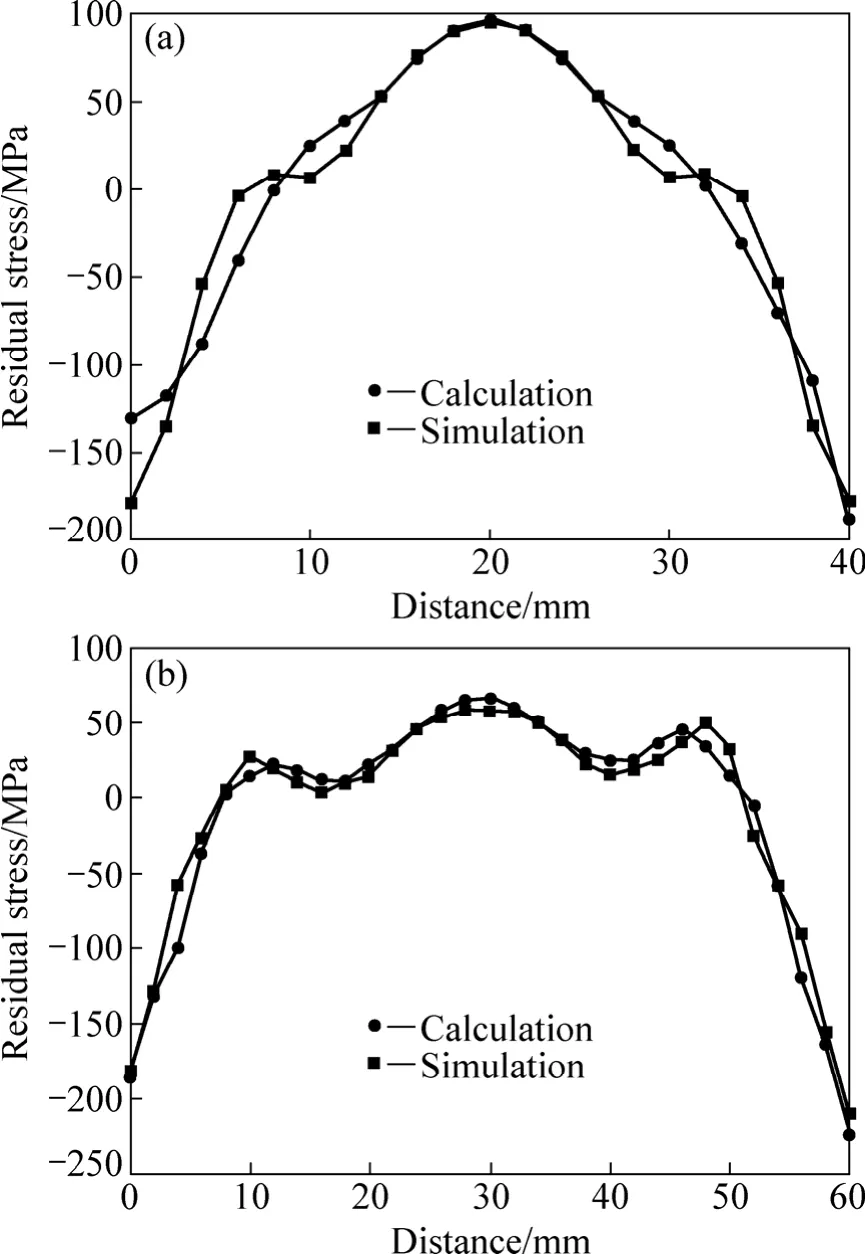
图6 不同尺寸试验的应力分布对比Fig. 6 Contrast of stress distributions of samples with different sizes: (a) d 80 mm×40 mm; (b) d 120 mm×60 mm

由图6可知，修正前两者计算平均偏差均大于50 MPa，但改进算法后只有前者在加工夹持部位的表面附近吻合误差较大，后者则吻合很好。表面处的应力波动主要与试样在完全环切完后小孔处于无约束自由状态下的应力释放有关，加之深孔法本来对表面应力较大的峰值缺乏表征能力，单纯依靠数学改进计算模型仍会产生一定的不确定性，就深孔法的应力计算不确定性还需要进一步研究。但就上述3组的验证效果来看，改进后的计算方法确实能够较好地描述区域应力场分布。

3 结论

1) 不论材料内部应力场分布是对称或非对称，改进后的深孔法计算模型，能够很好地描述材料内部应力分布状况。

2) 针对铝合金材料应力分布特点，在充分考虑材料变形趋势和不同尺寸对模型计算的影响前提下，算法的改进方法简便可靠，改进思路取得很好的效果。

3) 深孔法测试材料内部应力分布具有明显的优势，但是在表征表面应力时最好能够配合以X射线衍射技术进行标定和修正，从而可以获得更为准确的应力场分布。

4) 深孔法测试应力是一种实验力学测试方法，不同的实验方法、不同的环切直径与进给量都会对其结果产生一定的影响，所以其计算精确性还需要作进一步的不确定度分析

[1] 廖 凯, 吴运新, 龚 海, 张舒原. 积分法在铝合金厚板残余应力中的应用研究[J]. 中国有色金属学报, 2009, 19(6):1020-1024.LIAO Kai, WU Yun-xin, GONG Hai, ZHANG Shu-yuan.Application research of integral method to residual stress through-depth in aluminum alloy thick plate[J]. The Chinese Journal of Nonferrous Metal, 2009, 19(6): 1020-1024.

[2] 龚 海, 吴运新, 廖 凯. 铝合金厚板残余应力测试有效性分析[J]. 材料工程, 2010(1): 42-46.GONG Hai, WU Yun-xin, LIAO Kai. Analysis on validity of residual stress measurement methods for aluminum alloy thick-plate[J]. Journal of Materials Engineering, 2010(1): 42-46.

[3] SCHAJER G S, PRIME M B. Use of inverse solutions for residual stress measurement[J]. Journal of Engineering Materials and Technology, 2006, 128(3): 375-382.

[4] LIAO K, WU Y X. Effect of non-uniform stress characteristics on stress measurement in specimen[J]. Transactions of Nonferrous Metals Society of China, 2010, 20(5): 789-794.

[5] TIMOSHENKO S, GOODIER J N. Theory of elasticity[M]. 2nd ed. New York: Mcgraw-Hill, 1951: 70-86.

[6] DEWALD A, HILL M R. Improved data reduction for the deep-hole method of residual stress measurement[J]. Journal of Strain Analysis, 2003, 38(1): 65-78.

[7] GOUDAR D M, SMITH D J. Validation of mechanical strain relaxation methods for stress measurement[J]. Experimental Mechanics, 2013, 53(2): 267-286.

[8] HOSSEINZADEH F, MAHMOUDI A H, TRUMAN C E,SMITH D J. Application of deep hole drilling to the measurement and analysis of residual stress in steel shrik-fitted assemblies[J]. Strain, 2011, 47(2): 412-426.

[9] MAHMOUDI A H, HOSSAIN S, TRUMAN C E, SMITH D J,PAVIER M J. A new procedure to measure near yield residual stresses using the deep hole drilling technique[J]. Experimental Mechanics, 2009, 49(4): 595-604.

[10] MAHMOUDI A H, TRUMAN C E, SMITH D J, PAVIER M J.The effect of plasticity on the ability of the deep hole drilling technique to measure residual stress[J]. International Journal of Mechanical Sciences, 2011, 53: 978-988.

[11] BATEMAN M G, MILLER O H, PALMER T J, BREEN C E P,KINGSTON E J, SMITH D J, PAVIER M J. Measurement of residual stress in thick composite laminates using the deep-hole method[J]. International Journal of Mechanical Sciences, 2005,47(11): 1718-1739.

[12] DEWALD A T, HILL M R. Improved data reduction for the deep-hole method of residual stress measurement[J]. Strain Analysis, 2003, 38(1): 65-78.

[13] KINGSTON E J. Advances in the deep-hole drilling technique for residual stress measurement[D]. Boston: University of Bristol,2003.

[14] SKOURAS A, PAVIER M J, SHTERENLIKHT A. A spatial resolution of residual stress measurements using the deep hole drilling technique[C]//Proceedings of the ASME 2010 Pressure Vessels & Piping Dicision/K-PVP Conference. Washington:Bellevue, 2010: 25944.

[15] GOUDAR D M. Quantifying uncertainty in residual stress measurements using hole drilling techniques[D]. Boston:University of Bristol, 2011.

[16] SCHAJER G S, SMITH D J. Practical residual stress measurement methods[M]. United Kingdom: John Wiley Sons Ltd, 2013: 66-87.

[17] 张 炯, 徐济进, 吴静远, 陆 皓. 深孔法残余应力测量技术研究[J]. 热加工工艺, 2015, 44(2): 109-114.ZHANG Jiong, XU Ji-jin, WU Jing-yuan, LU Hao. Study on deep hole drilling residual stress measuring approach[J]. Hot Working Technology, 2015, 44(2): 109-114.