某机载雷达多自由度振动试验控制方法比较

司中柱，刘继承，易顺希

（1.南京电子技术研究所，南京 210039； 2. 苏州广博力学环境实验室，苏州 215011）

引言

机载雷达的故障大多数是由振动环境引起的，且这种振动环境是由多自由度振动合成的。目前由于试验设备和手段的限制，在产品的研制阶段只能分别用垂向和水平方向的单自由度振动代替实际的多自由度振动考核、验证产品的抗振设计。这种做法不仅效率低，且不能真实地模拟实际振动环境给试验样品带来的应力效应。

本文按某机载雷达单元实测的三自由度振动试验条件，在三轴振动台上采用不同的控制方法，对单元进行振动试验，并比较不同控制方法下单元在台面安装点处的振动响应。试验结果表明，长方阵控制中的坐标变换控制（Input/Output 控制）方法可实现真正意义上的平均控制，更真实地模拟装备的实际振动环境。

1 三轴振动试验方法

1.1 试验参考谱

单自由度振动只需要制定一个方向上的自谱PSD。多自由度振动不仅需要各自由度的自谱，还需要各自由度之间的互谱CSD，即：N 自由度的振动参考谱是一个N×N阶的矩阵。本文采用的三轴振动参考谱如图1～图3，获取过程详见参考文献[1]。

1.2 试验控制方法

多自由度试验除了需要控制各自由度上的振动量级外，还必须控制各自由度之间的相干函数与相位。本次试验主要采取以下两种振动控制方法：

1）方阵控制：该方法中使用的控制传感器数量等于振动台数量。本文中的振动台为三轴振动台，在三个正交的方向上各有一台振动台，控制传感器为安装在角点处的一个三向传感器。

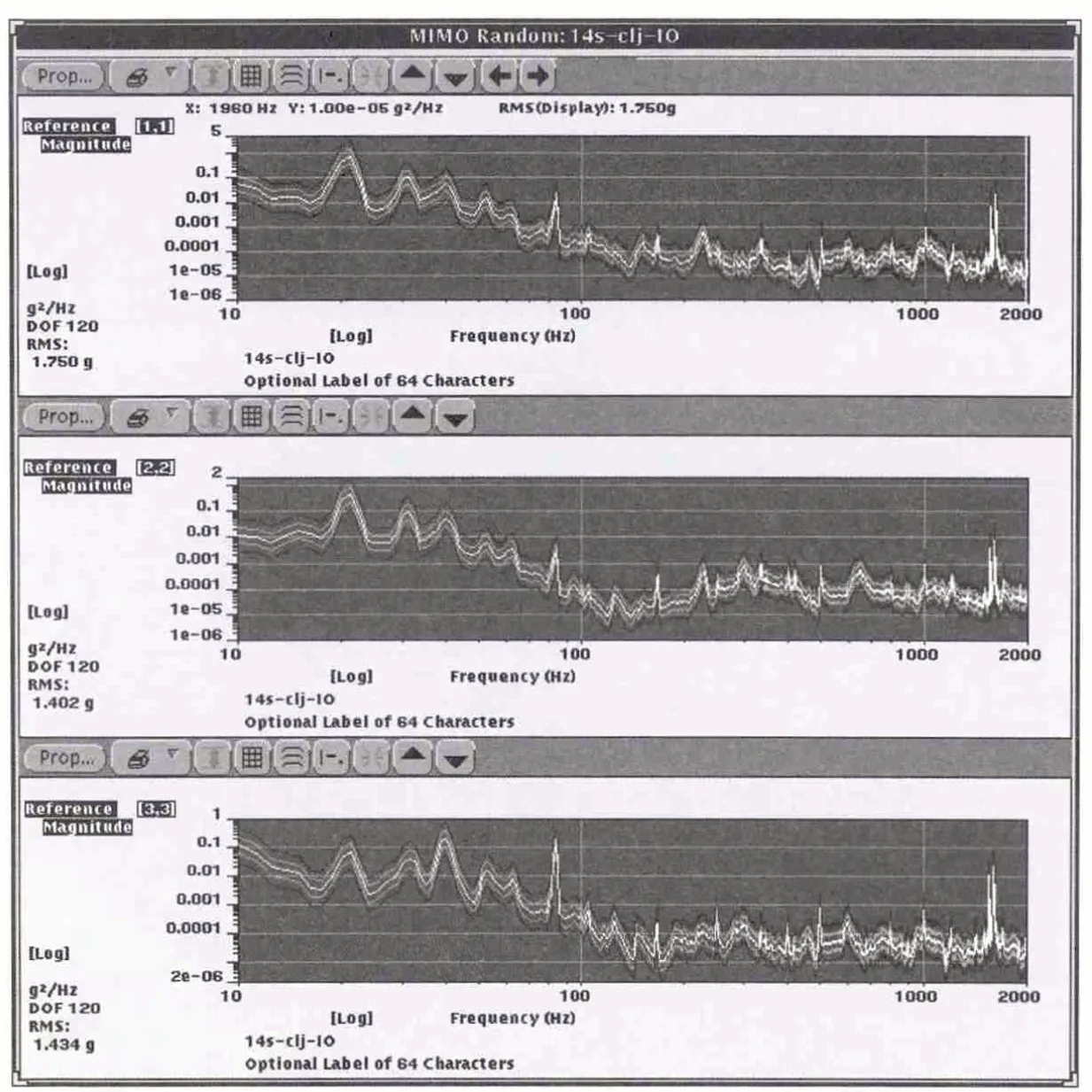
图1 功率谱密度函数参考谱PSDxx(上)、PSDyy（中）、PSDzz（下）

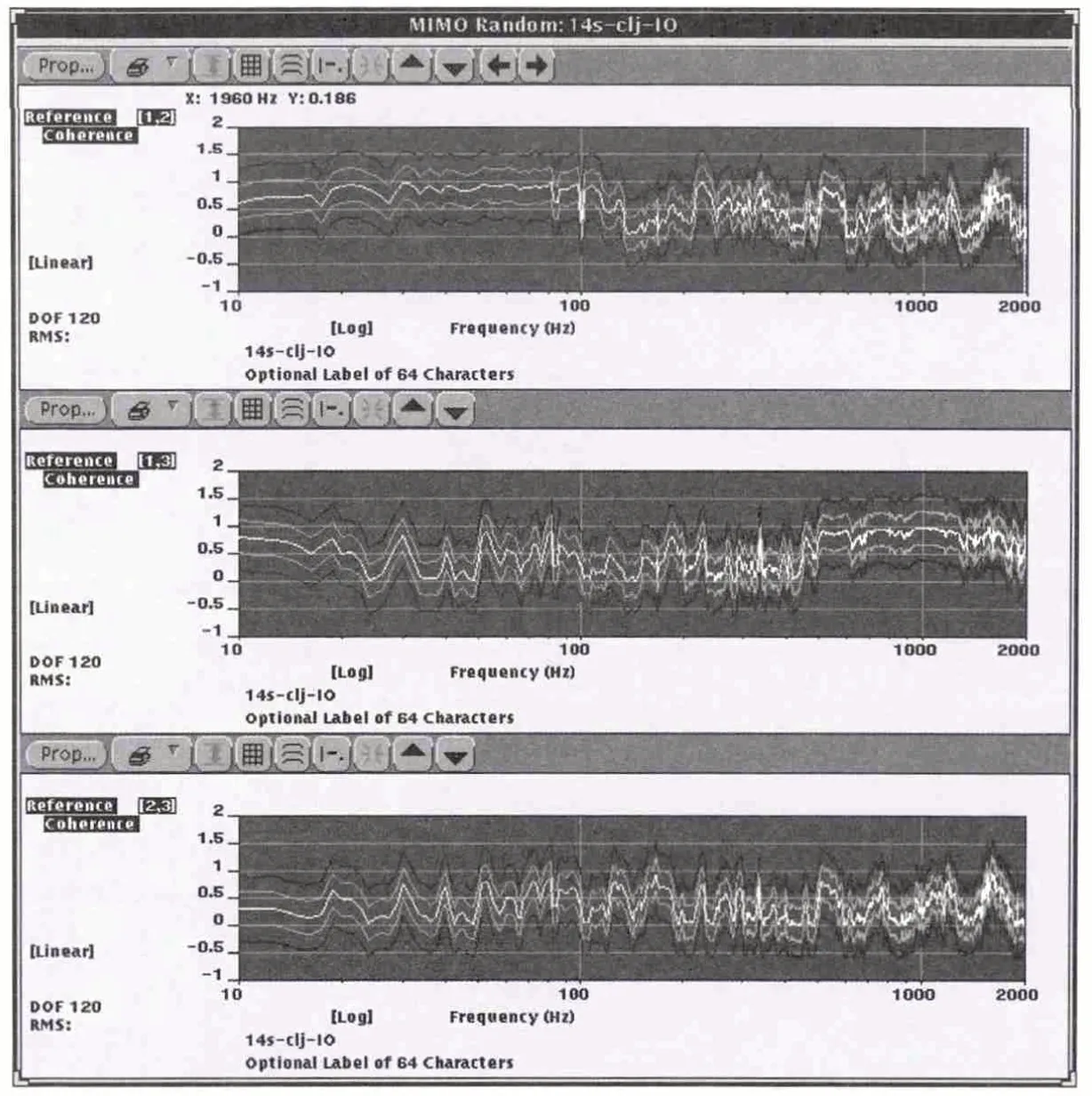
图2 相干函数参考谱γ2xy(上)、γ2xz（中）、γ2yz（下）

2）长方阵坐标变换控制（Input/Output 控制）：该方法属于长方阵控制方法的一种，控制传感器数量大于振动台数量，控制传感器的位置可根据试验需要确定。通过坐标变换，从控制传感器的加速度响应中提取出结构的刚体自由度加速度响应[2-3]，从而实现对试品刚体自由度的控制。

1.3 试验说明

雷达单元通过专用夹具固定在多自由度振动台台面上，安装图见图4。试验过程中，振动控制与测量加速度传感器的位置如图5，共布置了4 个三向传感器，位于夹具与试品底部连接处的四个角点处。方阵控制时控制传感器在2 号点；长方阵坐标变换控制（Input/Output控制）时采用下列坐标转换矩阵从{A1XA2YA2ZA3XA4Y}T中提取出结构的刚体自由度振动{x y z}T，并对刚体自由度进行控制：

振动控制仪采用Jaguar MIMO振动控制系统，振动台采用MAV-300-5H 三自由度（X、Y、Z）振动台。

2 不同振动控制方法四个角点处的加速度响应

方阵控制法四个角点处的加速度响应如图6，长方阵坐标变换控制法（Input/Output法）四个角点处的加速度响应如图7。

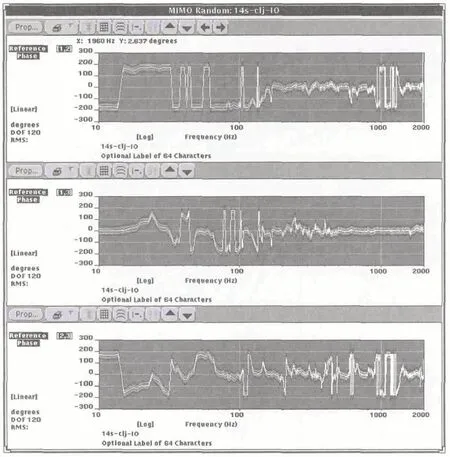
图3 相位参考谱θxy(上)、θxz（中）、θyz（下）

图4 雷达单元安装图

图5 传感器位置图

图6 方阵控制法1、2、3、4 号点响应PSDxx（上）、PSDyy（中）、PSDzz（下）

3 试验结果分析

试验的参考谱、实际控制谱、四个安装角点处结构响应RMS 值及四个角点处响应与参考谱RMS 值偏差见表1。

从表中可以看出：

1）采用长方阵坐标变换控制（Input/Output 控制），雷达单元在试品安装平台上四个安装角点处的加速度响应较为均匀，振动试验的控制效果明显优于方阵控制。其原因在于方阵控制时仅控制了2号点，其他点三点未参与控制，响应偏差较大；而长方阵坐标变换控制（Input/Output 控制）采用坐标转换矩阵，从{A1XA2YA2ZA3XA4Y}T中提取出结构的刚体自由度振动{x y z}T,实现了对结构刚体自由度振动的控制，振动在试品安装平台上的传递更为均匀，因此四个安装角点处的响应偏差相对较小。

2）水平轴向（X、Z）的控制效果优于垂向（Y）。采用控制效果更佳的长方阵坐标变换法，四个角点处水平向响应偏差在4.5%之内，垂向偏差则超过了65.7%。这是由于试品安装平台水平向有较大的刚度，而垂向的刚度相对较弱。

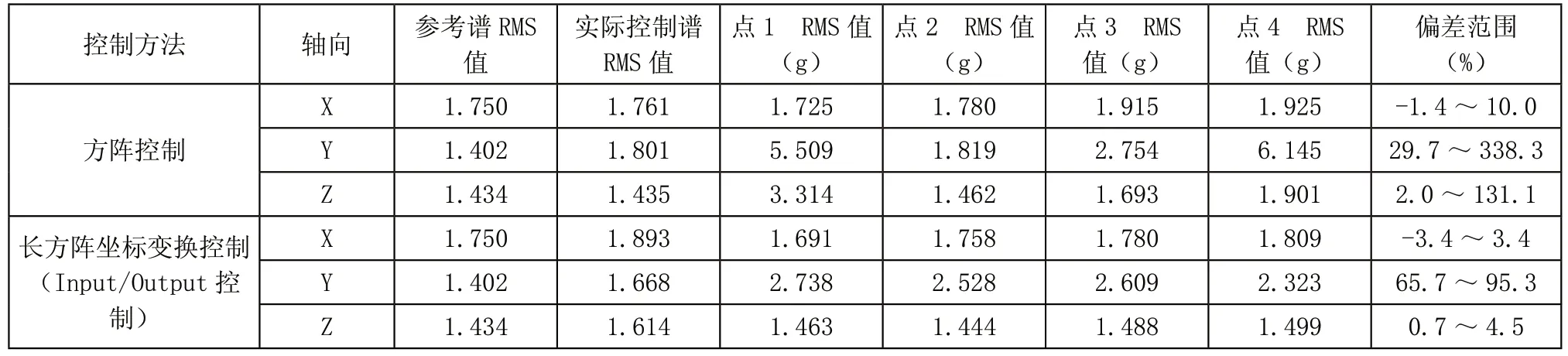
表1 两种控制方法结果的比较

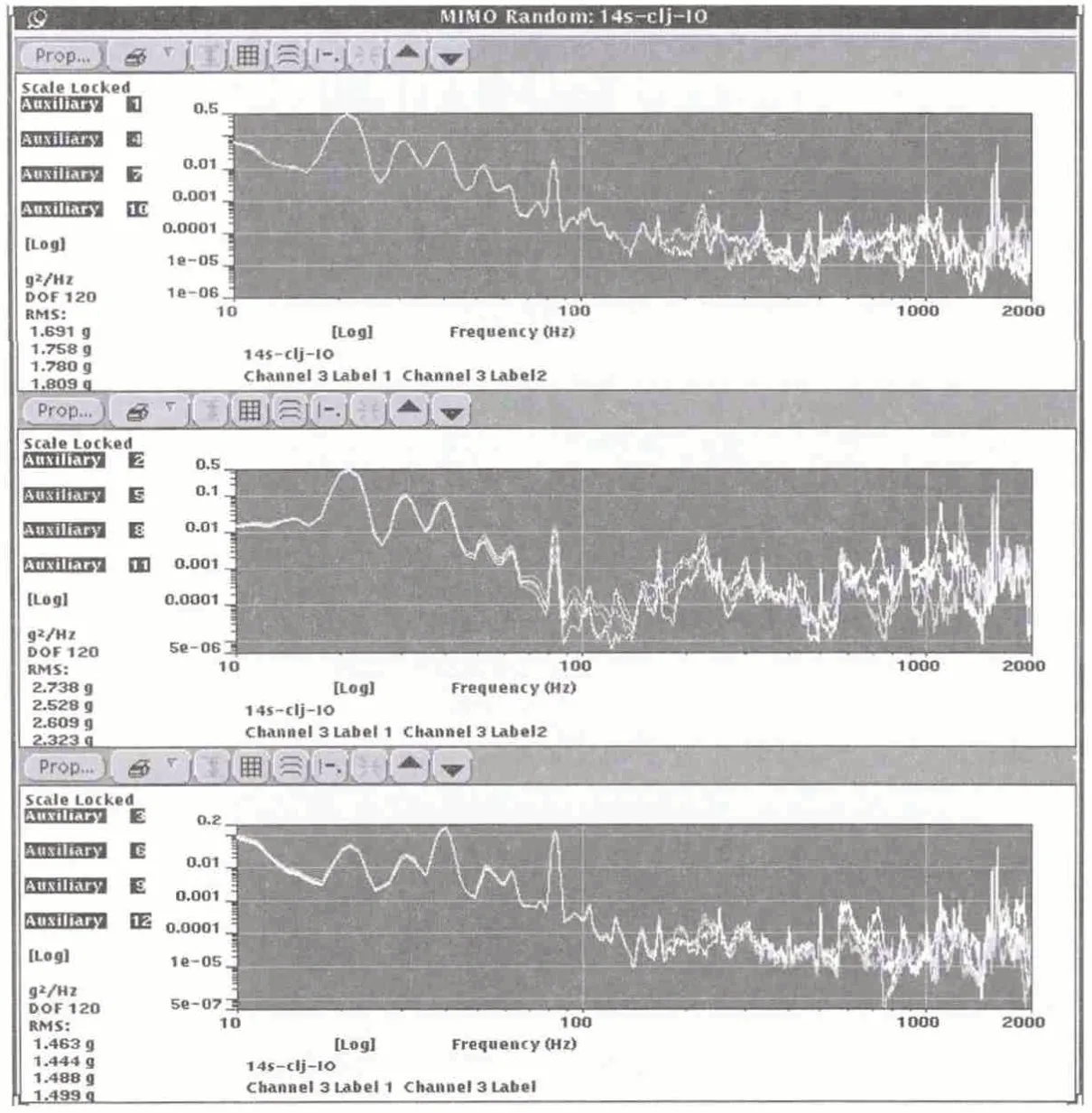
图7 长方阵坐标变换控制法1、2、3、4 号点响应PSDxx（上）、PSDyy（中）、PSDzz（下）

4 结论

试验结果表明：

1）方阵控制时传感器数量等于振动台数量，控制效果与单轴试验中的单点控制类似，振动在试品上的分布均匀性相对较差，仅适合结构刚度大、固有频率高的试品的多自由度试验；

2）长方阵坐标变换控制（Input/Output 控制）时控制传感器数量大于振动台数量，通过坐标变换对试品的刚体自由度进行控制，可实现真正意义上的平均控制，只要条件允许应优先采用此控制方法。

[1]司中柱，刘继承.某机载雷达多自由度振动参考谱制定研究[J].环境技术，2014,1：48-50.

[2]Underwood, M. and Keller, T. Applying Coordinate Transformations to Multi-DOF Shaker Control[J]. Sound and Vibration Magazine,2006,01.

[3]Hale, M and Fitz-Coy, N. On the Use of Linear Accelerometers in Six-DOF Laboratory Motion Replication: A Unif ied Time-Domain Analysis[C].76th Shock and Vibration Symposium, 2005.