基于ECC和零知识证明的盲签名方案设计与实现*

2015-03-25白永祥

通信技术 2015年10期

关键词：公钥对数椭圆

白永祥

(渭南职业技术学院，陕西渭南 714000)

基于ECC和零知识证明的盲签名方案设计与实现*

白永祥

(渭南职业技术学院，陕西渭南 714000)

椭圆曲线密码系统具有稳定的数学结构和较高的安全性，与目前流行的RSA公钥密码系统相比较有很大优势，成为当前研究的热点。基于椭圆曲线密码体制，设计和实现了一种高效安全的盲签名方案。首先，对相关概念及文献进行了分析与比较，介绍了椭圆曲线密码系统和盲签名的基本原理；其次，基于椭圆曲线密码系统的优势，设计了一种盲签名新方案.在方案中，为了不向签名者泄漏请求签名者的身份信息，消息发送者使用零知识证明协议隐藏了身份信息；最后，对设计方案的盲化、不可追踪性进行了分析，并与常见的盲签名算法进了分析比较，证明了本设计方案的高效性。

椭圆曲线密码系统；盲签名；零知识证明；椭圆曲线离散对数问题

0 引言

随着Internet的广泛应用，大量重要数据信息要通过互联网络到达目的地，在这个过程中，数据保密和安全认证显得十分重要。在传统签名模式中，手写签名是所签署的文件的物理部分，不可分割，而在计算机网络上无法实现，比如签名双方不在同一地方，甚至相隔千里，于是，数字签名技术便应运而生。数字签名的作用与传统的手写签名相同，只是数字签名是在双方不见面的情况下通过计算机网络完成的一种签名方式-电子签名。数字签名种类较多，这里只讨论一种很有发展潜力的特殊数字签名-盲签名。盲签名是David Chaum于1982年提出的一种签名方案，还给出了一个基于RSA的实现方案[1]，盲签名在电子投票和电子现金方面有着重要的应用。椭圆曲线密码系统是近年来的研究热点，它具有一定的优势，下面结合零知识证明技术，设计一种基于ECC的盲签名方案。

1 相关理论

1.1 椭圆曲线密码学

1985年，Neal Koblitz[2]和Victor Miller[3]各自独立地提出了一种公钥密码系统，称为椭圆曲线密码系统(Elliptic Curve Cryptosystem ，ECC)。ECC以其较少的系统参数、密钥短小、低带宽、实现快速、低能耗和更小的硬件处理器需求等特性，显示了其优越的性能。因此，要建立一个安全高效的密码系统，使用ECC是再合适不过的。应用于密码学的椭圆曲线一般使用模素数的椭圆曲线，这里p>3是素数，在p上的椭圆曲线同余方程如下：

y2(modp)≡x3+ax+b(modp)

它的所有解(x,y)∈p×p，定义O为一个特殊的无穷远点，它们一起构成p上的椭圆曲线y2=x3+ax+b。其中a,b∈p是满足4a3+27b2≠0的常量。

椭圆曲线E上的加法运算定义如下[4]：

假设P,Q为曲线上的两个点，且P=(x1,y1)，Q=(x2,y2)

(1)x1=x2且y2=-y1，则P+Q=O

(2)x1≠x2，则P+Q=R=(x3,y3)，R为PQ直线与椭圆曲线交点于X轴对称点。

x3=λ2-x1-x2

y3=λ(x1-x2)-y1

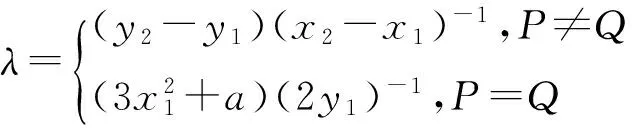
对于所有的P∈E，定义 P+O=O+P=P

1.2 零知识证明

1989年，Goldwasser等人提出了零知识证明(Zero-knowledge Proof Protocol，ZKP)的概念[5]。所谓零知识证明就是指用户A能够在不向用户B提供任何有用信息的前提下，使用户B确认用户A的某个论断是正确的。其实，零知识证明是一种涉及A、B双方或更多方的一种通信协议，即A、B双方或更多方为了完成一项任务，却不想泄漏相关信息所需要采取的一系列保护措施或步骤。用户A向用户B证明他知道或拥有某消息，而且用户A在证明过程中不会向用户B泄漏关于被证明消息的任何内容。近年来，随着人们网络信息安全意识的增强，零知识证明在密码学应用中非常广泛，例如将零知识证明用于消息或身份验证，可以防止信息泄漏。

1.3 盲签名

1.3.1 概念及特性

所谓盲签名[2]就是消息发送者Alice在发送消息之前，首先将消息m使用盲因子r进行盲化，再让签名者Bob对盲化后的消息m′进行签名，最后用户Alice对签名除去盲因子r，得到关于原消息的签名。在整个签名过程中，Bob无法获取所签名消息的内容，称这种特殊的数字签名技术为盲签名。

比如：消息发送者Alice先将隐蔽的信件放进信封里，为了得到Bob的签名，她在信封里放一张复写纸，当信件被密封在信封中时，任何人不能读它，包括Bob；Bob在信封上签名，他的签名便透过复写纸印写到信件上；信件返回给Alice后，Alice除去密封，并打开这个信封，得到签名。

盲签名除具有数字签名的一般性质外，还有自身的一些特征：

(1)机密性：签名者只对消息实施签名，而对所签署消息的内容是不可见的，关于这一点也存在一些争议，比如可能给犯罪分子造成一些可乘之机；

(2)不可追踪性：如果签名需要仲裁，就必须打开签名信息，签名者不能确定何时为何内容进行过签名；

(3)防伪造性：签名者使用自身的私钥实施签名，其他人都不可能假冒他的身份进行签名，这是一条最基本的特征；

(4)防抵赖性：签名者对某消息实施了签名后，如果发生争议，那么他无法否认曾经对消息的签名。

1.3.2 D. Chaum盲签名方案

1982年，D. Chaum提出了盲签名的概念，还给出了第一个基于RSA的实现方案[1]，具体过程如下：

Bob的公钥为e，私钥为d，n为一个公开模数，Alice打算让Bob对消息m进行盲签名。

(1)Alice随机选择k∈[1,n]，并计算t=mkemodn，隐藏m，然后发送t给Bob；

(2)Bob对t进行签名：td=(mke)dmodn；

(3)Alice要揭开td，进行计算：s=td/kmodn；

(4)取掉盲因子，结果为：s=mdmodn，

这是因为：td≡(mke)d≡mdkmodn，

所以td/k=mdk/k≡mdmodn。

后来，Chaum又设计了一些更复杂的盲签名算法，虽然这些在结构上都比较复杂，但是更为灵活。我们在设计盲签名方案时，必须考虑可操作性和高效性两个重要因素，这两个重要因素的实现都要依靠使用密钥的长度、盲签名算法和验证算法的复杂度。

2 研究现状

1982年，Chaum第一次提出了盲签名的概念[1]；1995年，Camenisch 等提出了基于离散对数问题的盲签名方案[6]，其缺点是不具有不可追踪性；2005年，吴和王证明Camenisch方案的不可跟踪性[7]，他们纠正了李的证明不可跟踪性,得出的结论是Camenisch仍然比李的方案更有效率；后来，Jena等人提出了两种新颖的盲签名方案[8]，然而却不能证明它们的正确性；最近Fan等人设计了一种攻击这些盲签名方案的方法[9]，因此，设计一种高效安全的盲签名方案十分必要。

椭圆曲线密码系统是一种公认的安全高效的公钥密码系统。文献[10]已证明ECC效率比基于大整数因子分解或离散对数的公钥密码系统高10倍以上，当然这些得益于ECC的计算开销小、短密钥和低带宽。ECC的安全性主要还是基于椭圆曲线离散对数难解问题之上。同大整数因子分解问题和离散对数问题一样，目前很难找到一种有效算法解决椭圆曲线离散对数据问题，椭圆曲线离散对数难解问题比大整数因子问题和离散对数问题更难解决。文献[11]提出了一种基于椭圆曲线离散对数问题的签密方案。所有这些方案既有优点，又有缺点，下面基于前人的研究成果，提出一种比较合理的盲签名方案。

3 方案设计

方案包含了以下4个步骤：初始化及密钥生成、消息盲化、签名、去盲化和验证，除去初始化及密钥生成外，方案流程如图1所示。

图1 方案流程

3.1 初始化

在初始化阶段，选择一条安全的有限域Fp上的椭圆曲线Ep(a,b)，并产生一些公共参数，选择基点等。

例如：

y2modp=(x3+ax+b)modp

a=1,b=1,x=10,y=6,p=13

62mod13=(103+10+1)mod13

10=10

同样，可以计算出有限域椭圆曲线上的所有点，并运用加法原则和倍乘计算出对应的点，公式如下：

点加法：P+Q=R，且P≠Q

点倍乘：2P=R，且P=Q

椭圆曲线密码系统的安全性，主要取决于定义在椭圆曲线上的有限阿贝尔群中点的个数。在有限群Ep(a,b)中，点的个数N的范围是[12]：

所以，Ep(a,b)上点的个数约等于Zp中元素的个数，即p个元素。

(2)密钥生成

计算出椭圆曲线Ep(a,b)上的所有点，选择基点G=(x1,y1)，G的循环群阶为n，且nG=O，O为无穷远点。Ep(a,b)、G和n是公共参数。公钥和私钥产生过程如下：

①请求签名者随机在椭圆曲线上选择点,并计算出公钥和私钥；

②签名者随机选择一个小于n的整数ds，作为私钥，再计算出公钥Ps=ds×G，该公钥也是Ep(a,b)中的一个点；

③签名者再随机选择整数i，i∈Fp，然后他计算出点R1=iG，签名者发回R1给请求签名者；

3.2 盲化

发送者需要对消息m签名后再发送给接收者，为了防止签名者知道消息内容，发送者需要对消息进行盲化后再发送给最终的接收者，整个过程如图2所示。

图2 盲签名过程

发送者在E(Fp)随机选择一个点G'(x1,y1)，x1作为盲因子，然后再进行以下计算：

(2)再计算r=x0modn；

(3)对消息m进行盲化：m′=x1rm+y1；

(4)发送者把盲化后的消息传送给签名者。

3.3 证明和签名

签名者收到要求签名的盲化后的消息m′后，使用零知识技术计算消息的真实值，验证者再使用零知识技术进行验证。签名者通过向发送者询问e的值{0,1}，验证是否和发送者发送的消息相同，图3和图4为零知识证明过程。

图3 e=1的证明过程

图4 e=0的证明过程

签名者收到要签名的消息后，进行签名：s′=dsm′+i，然后把盲签名结果s′发送给请求签名者。

3.4 去盲化

3.5 验证

验证者通过式子S=rmPs+R进行签名验证，对消息m签名(R,S) 的有效性证明如下[13]：

图5 盲签名方案流程

4 方案分析

4.1 安全性能分析

我们的方案具有盲签名的基本特性，即不可追踪性、不可伪造性、不可抵赖性及签名者不能识别签名消息的内容等。方案的安全性基于椭圆曲线离散对数问题的难解性。

(1)消息盲化

(2)不可追踪性

签名者也不可能依据参数(i,R1,m′,s′)对所签名文件进行追踪，因为签名者不可能知道要求签名者的参数(x1,y1,r)，要进行逆推导，就要面临解决椭圆曲线离散对数问题的难题。

4.2 效率分析

我们对椭圆曲线上点加与点乘的时间复杂度进行了研究分析，相对于点乘的逆运算，点加所用时间很短，这里主要讨论点乘和逆运算的情况。

下面是我们的方案与常见盲签名方案所用时间对比如表1所示。

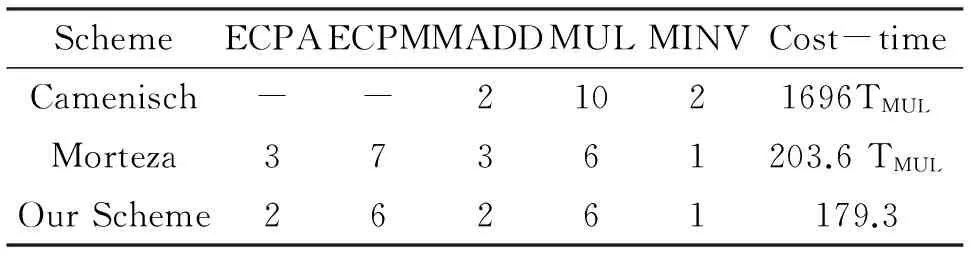
表1 3种方案时间开销比较分析

从表1中数据看出我们的方案相对较好，事实上我们的盲签名方案的安全性与另两个方案相同。用户和签名者在签名时只需要很少的操作步骤，所以我们的方案更有效。

5 结语

本文提出了一种基于椭圆曲线离散对数问题和零知识协议的盲签名方案，证明了方案的安全性和不可追踪性。由于椭圆曲线密码算法占用内存少，运算速度快等原因，所以本方案的效率较高，同时本方案基于椭圆曲线离散对数问题，实现了以较短的密钥与RSA相同安全性的效果。方案还基于零知识协议，使签名请求者向签名者证明自己知道或拥有某消息，但又未向签名泄漏任何消息内容和身份信息，所以，本方案能很好的应用于电子现金系统的支付，也能应用于匿名投票选举。

[1] David Chaum. Blind Signatures for Untraceable Payments[C]// In Advances in Cryptology CRYPTO′82.California: Springer，1982：199-203.

[2] Koblitz N. Elliptic Curve Cryptosystems[J]. Mathematics of Compution,1987(48)：203-209.

[3] Miller V. Use of Elliptic Curves in Cryptography[C]// Advances in Cryptology-CRYPTO’85(LNCS 218).Santa Barbara：Springer，1986：417-426.

[4] 白永祥.一种高效群签名方案的设计与分析[J].通信技术，2015(48)：214-218. BAI Yong-xiang. Design and Analysis of Efficient Group Signature Scheme[J].Communications Technology,2015(48)：214-218.

[5] Goldwasser, Micali, Rackoff. Knowledge Complexity of Interactive Proof-Systems[J].SIAM Journal of Computing.1989 (18)：186-208.

[6] Camenisch, Piveteau, Markus . Blind Signatures based on the Discrete Logarithm Problem[C]// In Advances in Cryptology Eurocrypt′94. Perugia:Springer 1994:428-432.

[7] WU Ting ,WANG Jin-rong. Comment: A New Blind Signature based on the Discrete Logarithm Problem for Untraceability[J]. Applied Mathematics and Computation, 2005,170(2)：999-1005.

[8] Jena, Kumar, Majhi. A Novel Untraceable Blind Signature based on Elliptic Curve Discrete Logarithm Problem[J]. IJCSNS International Journal of Computer Science and Network Security, 2007,7(6)：269-275.

[9] FAN, GUAN,LIN Dai-rui . Cryptanalysis of Lee Hwang-Yang Blind Signature Scheme[J]. Computer Standards & Interfaces, 2009,31(2)：319-320.

[10] Vanstone. Elliptic Curve Cryptosystem-the Answer to Strong, Fast Public Key Cryptography for Securing Constrained Environments[J]. Information Security Technical Report, 1997 (2)：78-87.

[11] Amounas, Sadki , Kinani. An Efficient Signcryption Scheme based on the Elliptic Curve Discrete Logarithm Problem[J]. International Journal of Information & Network Security (IJINS), 2013 (2)： 253-259.

[12] [加]Douglas R Stinson. 密码学原理与实践[M].第3版.冯登国等译. 北京：电子工业出版社, 2015：201-207. Douglas R Stinson. Cryptography Theory and Practice [M]. Third Edition. Beijing: Publishing House of Electronic Industry, 2015：201-207.

[13] Amounas, Kinani. Proposed Developements of Blind Signature Scheme based on ECC[J]. Computer Engineering and Applications 2013(2)：151-160.

Design and Implementation of Blind Signature Scheme based on ECC and Zero-Knowledge Proof

BAI Yong-xiang

(Weinan Vocational & Technical College, Weinan Shaanxi 714000，China)

Owing to its robust mathematical structure and high security, elliptic curve cryptosystem enjoys obvious superiority as compared with current RSA public key cryptosystem, thus becomes the hottest research topic. Based on elliptic curve cryptosystem, an efficient and secure blind signature scheme is designed and implemented. The related concepts and documents are analyzed and compared, and the basic principles of elliptic curve cryptosystem and blind signature also described in this paper. Finally, a novel scheme of blind signature based on the advantages of elliptic curve cryptosystem is designed. In this scheme, message sender hides the identity information through zero-knowledge proof protocol, thus leaking no identity information of the request signer to the signer. Finally the blinding and untractability of the design scheme are analyzed, and comparison of and analysis on several common blind signature algorithms indicate the high efficiency of this design scheme.

elliptic curve cryptosystem； blind signature ；zero knowledge proof； elliptic curve discrete logarithm problem

10.3969/j.issn.1002-0802.2015.10.015

2015-05-21；

2015-09-03 Received date:2015-05-21；Revised date：2015-09-03

渭南市科技创新扶持资金资助(No.2013JCYJ-6)；渭南职业技术学院教研基金项目资助(No.WZJY201303)

Foundation Item：Weinan Fund Support Science and Technology Innovation(No.2013JCYJ-6)；Teaching & Research Project Fund of Weinan Vocational & Technical College (No. WZJY201303)

TP309.7

1002-0802(2015)10-1174-05